鲁教版数学八年级上册第五章 平行四边形综合测评(含答案)
文档属性
| 名称 | 鲁教版数学八年级上册第五章 平行四边形综合测评(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 226.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-13 00:00:00 | ||
图片预览

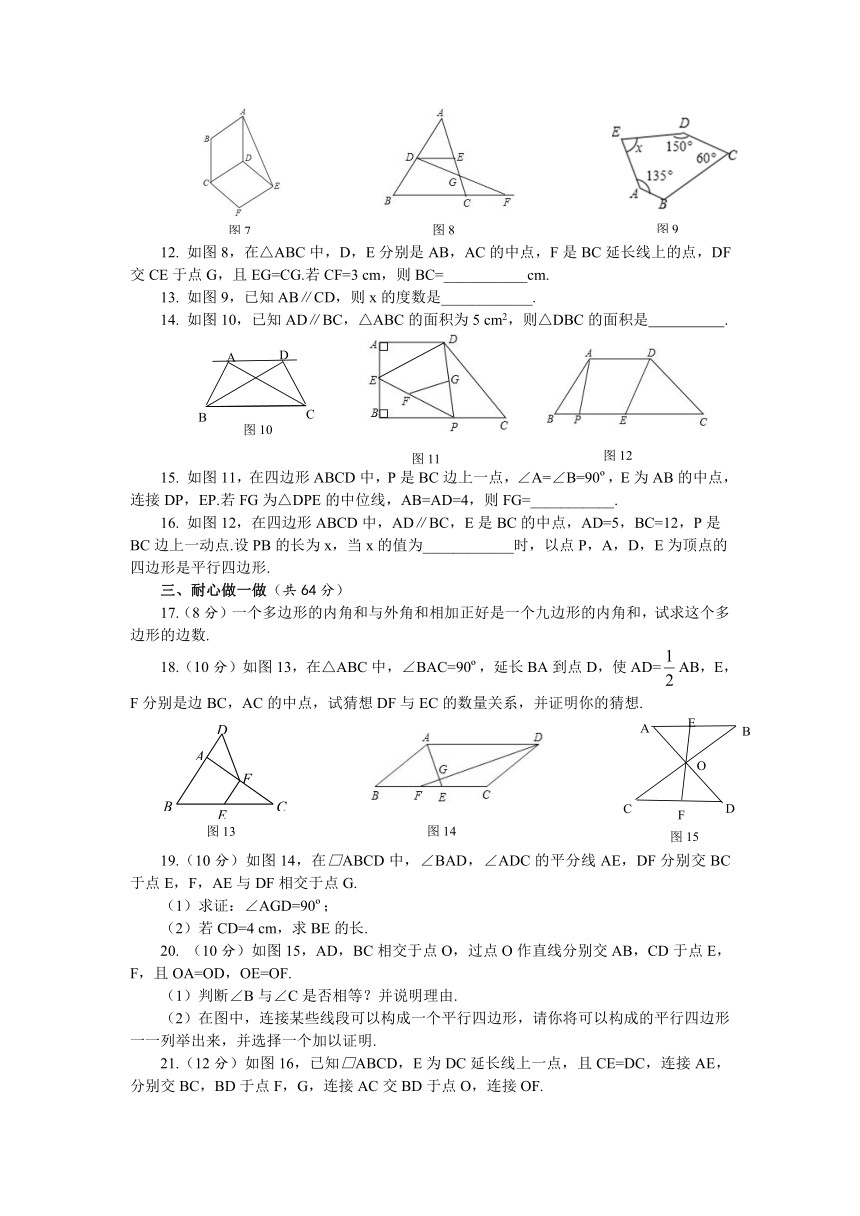
文档简介
平行四边形
综合测评
一、精心选一选(每小题3分,共24分)
1.
一个多边形的内角和与外角和的度数之比为2∶1,则这个多边形的边数为(
)
A.
3
B.
4
C.
5
D.
6
2.
如图1,已知□ABCD,对角线AC,BD相交于点O,将△ADO平移至△BCE的位置,则图中与CE相等的线段有(
)21
cnjy
com
A.
4条
B.
3条
C.
2条
D.
1条
3.
如图2,在△ABC中,点D在边BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若DC=16
cm,则MN的长为(
)21世纪教育网版权所有
A.
8
cm
B.
10
cm
C.
12
cm
D.
14
cm
4.
已知四边形ABCD的四条边长度依次为a,b,c,d,(a-c)2+(b-d)2=0,且a,c与b,d分别是对边,则四边形ABCD的形状是(
)www.21-cn-jy.com
A.
任意四边形
B.
对角线互相平分的四边形
C.
对角线相等的四边形
D.
对角线互相垂直的四边形
5.
一个正多边形的内角和为3240 ,则该多边形的一个外角是(
)
A.
15
B.
18
C.
20
D.
36
6.
如图3,将△ABC沿着它的中位线DE折叠,点A落在F处.若∠C=120 ,∠A=20 ,则∠FEB的度数是(
)【来源:21·世纪·教育·网】
A.
80
B.
100
C.
120
D.
140
7.
如图4,E是□ABCD的一边AD上任一点,若△EBC的面积为S1,□ABCD的面积为S,则S1与S的关系是(
)www-2-1-cnjy-com
A.
S1=S
B.
S1C.
S1>S
D.
无法确定
8.
如图5,在□ABCD中,E,F分别为边AD,BC上的点,且AE=CF,连接AF,BE相交于点M,连接CE,DF相交于点N,则图中平行四边形(不包含□ABCD)的个数为(
)
A.
4个
B.
3个
C.
2个
D.
1个
二、细心填一填(每小题4分,共32分)
9.
如图6,已知DE∥AC,要使四边形AEDF是平行四边形,则需要添加的条件是_____________(只填一个).【来源:21cnj
y.co
m】
10.
已知过n边形的一个顶点有7条对角线,则n边形的内角和为
.
11.
如图7,四边形ABCD和四边形CDEF都是平行四边形.若∠BAD=60 ,∠F=110 ,则∠ADE的度数为___________.【出处:21教育名师】
21世纪教育网
12.
如图8,在△ABC中,D,E分别是AB,AC的中点,F是BC延长线上的点,DF交CE于点G,且EG=CG.若CF=3
cm,则BC=___________cm.【版权所有:21教育】
13.
如图9,已知AB∥CD,则x的度数是____________.
14.
如图10,已知AD∥BC,△ABC的面积为5
cm2,则△DBC的面积是
.
21世纪教育网
15.
如图11,在四边形ABCD中,P是BC边上一点,∠A=∠B=90 ,E为AB的中点,连接DP,EP.若FG为△DPE的中位线,AB=AD=4,则FG=___________.
16.
如图12,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,P是BC边上一动点.设PB的长为x,当x的值为____________时,以点P,A,D,E为顶点的四边形是平行四边形.2-1-c-n-j-y
三、耐心做一做(共64分)
17.(8分)一个多边形的内角和与外角和相加正好是一个九边形的内角和,试求这个多边形的边数.
18.(10分)如图13,在△ABC中,∠BAC=90 ,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
19.(10分)如图14,在□ABCD中,∠BAD,∠ADC的平分线AE,DF分别交BC于点E,F,AE与DF相交于点G.21世纪教育网21教育网
(1)求证:∠AGD=90 ;
(2)若CD=4
cm,求BE的长.
20.
(10分)如图15,AD,BC相交于点O,过点O作直线分别交AB,CD于点E,F,且OA=OD,OE=OF.21教育名师原创作品
(1)判断∠B与∠C是否相等?并说明理由.
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来,并选择一个加以证明.21
cnjy
com
21.(12分)如图16,已知□ABCD,E为DC延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF.
(1)求证:△ABF≌△CEF;
(2)判断AB与OF的位置关系和大小关系,并证明你的结论.
(3)在解决(1)、(2)问题的过程中,主要用了“平行四边形”一章中的哪些知识点,请写出三个:______________、________________、_________________.
21世纪教育网
22.(12分)提出命题:如图17,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180 -∠A,∠2+∠4=180 ―∠C,∠A=∠C,
∴
∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(
)
A.
∠A∶∠B∶∠C∶∠D=1∶2∶3∶4
B.
∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C.
∠A∶∠B∶∠C∶∠D=2∶3∶3∶2
D.
∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
参考答案
一、1.
D
2.
C
3.
A
4.
B
5.
B
6.
B
7.
A
8.
B
二、9.
答案不唯一,如DF∥AB
10.
1440
11.
130
12.
6
13.
75
14.
5
cm2
15.
16.
1或1121cnjy.com
三、17.
解:设这个多边形的边数为n,则根据题意,得
(n-2)·180 +360 =(9-2)×180 ,解得n=7.所以这个多边形的边数为7.
18.
解:猜想DF=EC.
证明:因为E,F分别是边BC,AC的中点,所以AF=FC,EF=AB,EF∥AB.
所以∠EFC=∠BAC=90 .
因为AD=AB,所以AD=EF.因为∠DAF=90 ,所以∠EFC=∠DAF.
所以△ADF≌△FEC.所以DF=EC.
19.
解:(1)因为四边形ABCD是平行四边形,所以∠BAD+∠ADC=180 .
因为AE,DF分别平分∠BAD,∠ADC,所以∠DAG=∠BAD,∠ADG=∠ADC.
所以∠DAG+∠ADG=×180 =90 .所以∠AGD=180 -90 =90 .
(2)因为四边形ABCD是平行四边形,所以AB=CD,AD∥BC.所以∠DAE=∠AEB.
因为AE平分∠BAD,所以∠DAE=∠BAE.所以∠BAE=∠AEB.所以AB=BE.所以BE=CD.21·cn·jy·com
因为CD=4
cm,所以BE=4
cm.
20.
解:(1)∠B=∠C.
理由:因为OA=OD,∠AOE=∠DOF,OE=OF.所以△AOE≌△DOF.所以∠A=∠D.
因为∠AOB=∠DOC,所以∠B=∠C.
(2)连接AF,ED,可构成□AEDF;连接CE,BF,可构成□BECF;连接AC,BD,可构成□ABDC.2·1·c·n·j·y
选择□AEDF证明:因为△AOE≌△DOF,所以AE=DF,∠BAD=∠CDA.所以AE∥DF.所以四边形AEDF是平行四边形.21·世纪
教育网
21.
解:(1)因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD.所以∠BAE=∠E.
因为CE=DC,所以AB=CE.因为∠AFB=∠EFC,所以△ABF≌△CEF.
(2)AB∥OF,AB=2OF.
证明:因为△ABF≌△CEF,所以BF=FC.
因为四边形ABCD是平行四边形,所以AO=OC.
所以OF是△ABC的中位线.所以AB∥OF,AB=2OF.
(3)答案不唯一,如:平行四边形的对边分别相等;平行四边形的对边分别平行;平行四边形的对角线互相平分;三角形的中位线平行于第三边,且等于第三边的一半
22.
解:(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=∠3.
正确证明:因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C,∠ABC=∠ADC,所以2∠A+
2∠ABC=360°.所以∠A+∠ABC=180°.所以AD∥BC.同理∠A+∠ADC=180°.所以AB∥CD.所以四边形ABCD是平行四边形.
(2)两组对角分别相等的四边形是平行四边形
(3)B
图2
A
C
O
D
B
图1
E
图3
S1
图4
图6图5
图8
图9
图7
图12
图11
A
B
C
D
图10
图15
E
B
C
D
A
F
O
C
F
D
E
B
A
图13
图14
图17
O
G
C
F
D
E
B
A
图16
综合测评
一、精心选一选(每小题3分,共24分)
1.
一个多边形的内角和与外角和的度数之比为2∶1,则这个多边形的边数为(
)
A.
3
B.
4
C.
5
D.
6
2.
如图1,已知□ABCD,对角线AC,BD相交于点O,将△ADO平移至△BCE的位置,则图中与CE相等的线段有(
)21
cnjy
com
A.
4条
B.
3条
C.
2条
D.
1条
3.
如图2,在△ABC中,点D在边BC上,BD=AB,BM⊥AD于点M,N是AC的中点,连接MN.若DC=16
cm,则MN的长为(
)21世纪教育网版权所有
A.
8
cm
B.
10
cm
C.
12
cm
D.
14
cm
4.
已知四边形ABCD的四条边长度依次为a,b,c,d,(a-c)2+(b-d)2=0,且a,c与b,d分别是对边,则四边形ABCD的形状是(
)www.21-cn-jy.com
A.
任意四边形
B.
对角线互相平分的四边形
C.
对角线相等的四边形
D.
对角线互相垂直的四边形
5.
一个正多边形的内角和为3240 ,则该多边形的一个外角是(
)
A.
15
B.
18
C.
20
D.
36
6.
如图3,将△ABC沿着它的中位线DE折叠,点A落在F处.若∠C=120 ,∠A=20 ,则∠FEB的度数是(
)【来源:21·世纪·教育·网】
A.
80
B.
100
C.
120
D.
140
7.
如图4,E是□ABCD的一边AD上任一点,若△EBC的面积为S1,□ABCD的面积为S,则S1与S的关系是(
)www-2-1-cnjy-com
A.
S1=S
B.
S1
S1>S
D.
无法确定
8.
如图5,在□ABCD中,E,F分别为边AD,BC上的点,且AE=CF,连接AF,BE相交于点M,连接CE,DF相交于点N,则图中平行四边形(不包含□ABCD)的个数为(
)
A.
4个
B.
3个
C.
2个
D.
1个
二、细心填一填(每小题4分,共32分)
9.
如图6,已知DE∥AC,要使四边形AEDF是平行四边形,则需要添加的条件是_____________(只填一个).【来源:21cnj
y.co
m】
10.
已知过n边形的一个顶点有7条对角线,则n边形的内角和为
.
11.
如图7,四边形ABCD和四边形CDEF都是平行四边形.若∠BAD=60 ,∠F=110 ,则∠ADE的度数为___________.【出处:21教育名师】
21世纪教育网
12.
如图8,在△ABC中,D,E分别是AB,AC的中点,F是BC延长线上的点,DF交CE于点G,且EG=CG.若CF=3
cm,则BC=___________cm.【版权所有:21教育】
13.
如图9,已知AB∥CD,则x的度数是____________.
14.
如图10,已知AD∥BC,△ABC的面积为5
cm2,则△DBC的面积是
.
21世纪教育网
15.
如图11,在四边形ABCD中,P是BC边上一点,∠A=∠B=90 ,E为AB的中点,连接DP,EP.若FG为△DPE的中位线,AB=AD=4,则FG=___________.
16.
如图12,在四边形ABCD中,AD∥BC,E是BC的中点,AD=5,BC=12,P是BC边上一动点.设PB的长为x,当x的值为____________时,以点P,A,D,E为顶点的四边形是平行四边形.2-1-c-n-j-y
三、耐心做一做(共64分)
17.(8分)一个多边形的内角和与外角和相加正好是一个九边形的内角和,试求这个多边形的边数.
18.(10分)如图13,在△ABC中,∠BAC=90 ,延长BA到点D,使AD=AB,E,F分别是边BC,AC的中点,试猜想DF与EC的数量关系,并证明你的猜想.
19.(10分)如图14,在□ABCD中,∠BAD,∠ADC的平分线AE,DF分别交BC于点E,F,AE与DF相交于点G.21世纪教育网21教育网
(1)求证:∠AGD=90 ;
(2)若CD=4
cm,求BE的长.
20.
(10分)如图15,AD,BC相交于点O,过点O作直线分别交AB,CD于点E,F,且OA=OD,OE=OF.21教育名师原创作品
(1)判断∠B与∠C是否相等?并说明理由.
(2)在图中,连接某些线段可以构成一个平行四边形,请你将可以构成的平行四边形一一列举出来,并选择一个加以证明.21
cnjy
com
21.(12分)如图16,已知□ABCD,E为DC延长线上一点,且CE=DC,连接AE,分别交BC,BD于点F,G,连接AC交BD于点O,连接OF.
(1)求证:△ABF≌△CEF;
(2)判断AB与OF的位置关系和大小关系,并证明你的结论.
(3)在解决(1)、(2)问题的过程中,主要用了“平行四边形”一章中的哪些知识点,请写出三个:______________、________________、_________________.
21世纪教育网
22.(12分)提出命题:如图17,在四边形ABCD中,∠A=∠C,∠ABC=∠ADC,求证:四边形ABCD是平行四边形.
小明提供了如下解答过程:
证明:连接BD.
∵∠1+∠3=180 -∠A,∠2+∠4=180 ―∠C,∠A=∠C,
∴
∠1+∠3=∠2+∠4.
∵∠ABC=∠ADC,
∴∠1=∠4,∠2=∠3.
∴AB∥CD,AD∥BC.
∴四边形ABCD是平行四边形(两组对边分别平行的四边形是平行四边形).
反思交流:(1)请问小明的解法正确吗?如果有错,说明错在何处,并给出正确的证明过程.
(2)用语言叙述上述命题:___________________________________________________.
运用探究:(3)下列条件中,能确定四边形ABCD是平行四边形的是(
)
A.
∠A∶∠B∶∠C∶∠D=1∶2∶3∶4
B.
∠A∶∠B∶∠C∶∠D=1∶3∶1∶3
C.
∠A∶∠B∶∠C∶∠D=2∶3∶3∶2
D.
∠A∶∠B∶∠C∶∠D=1∶1∶3∶3
参考答案
一、1.
D
2.
C
3.
A
4.
B
5.
B
6.
B
7.
A
8.
B
二、9.
答案不唯一,如DF∥AB
10.
1440
11.
130
12.
6
13.
75
14.
5
cm2
15.
16.
1或1121cnjy.com
三、17.
解:设这个多边形的边数为n,则根据题意,得
(n-2)·180 +360 =(9-2)×180 ,解得n=7.所以这个多边形的边数为7.
18.
解:猜想DF=EC.
证明:因为E,F分别是边BC,AC的中点,所以AF=FC,EF=AB,EF∥AB.
所以∠EFC=∠BAC=90 .
因为AD=AB,所以AD=EF.因为∠DAF=90 ,所以∠EFC=∠DAF.
所以△ADF≌△FEC.所以DF=EC.
19.
解:(1)因为四边形ABCD是平行四边形,所以∠BAD+∠ADC=180 .
因为AE,DF分别平分∠BAD,∠ADC,所以∠DAG=∠BAD,∠ADG=∠ADC.
所以∠DAG+∠ADG=×180 =90 .所以∠AGD=180 -90 =90 .
(2)因为四边形ABCD是平行四边形,所以AB=CD,AD∥BC.所以∠DAE=∠AEB.
因为AE平分∠BAD,所以∠DAE=∠BAE.所以∠BAE=∠AEB.所以AB=BE.所以BE=CD.21·cn·jy·com
因为CD=4
cm,所以BE=4
cm.
20.
解:(1)∠B=∠C.
理由:因为OA=OD,∠AOE=∠DOF,OE=OF.所以△AOE≌△DOF.所以∠A=∠D.
因为∠AOB=∠DOC,所以∠B=∠C.
(2)连接AF,ED,可构成□AEDF;连接CE,BF,可构成□BECF;连接AC,BD,可构成□ABDC.2·1·c·n·j·y
选择□AEDF证明:因为△AOE≌△DOF,所以AE=DF,∠BAD=∠CDA.所以AE∥DF.所以四边形AEDF是平行四边形.21·世纪
教育网
21.
解:(1)因为四边形ABCD是平行四边形,所以AB=CD,AB∥CD.所以∠BAE=∠E.
因为CE=DC,所以AB=CE.因为∠AFB=∠EFC,所以△ABF≌△CEF.
(2)AB∥OF,AB=2OF.
证明:因为△ABF≌△CEF,所以BF=FC.
因为四边形ABCD是平行四边形,所以AO=OC.
所以OF是△ABC的中位线.所以AB∥OF,AB=2OF.
(3)答案不唯一,如:平行四边形的对边分别相等;平行四边形的对边分别平行;平行四边形的对角线互相平分;三角形的中位线平行于第三边,且等于第三边的一半
22.
解:(1)小明的解法不正确,错在推出∠1+∠3=∠2+∠4后,由∠ABC=∠ADC,不能直接推出∠1=∠4,∠2=∠3.
正确证明:因为∠A+∠ABC+∠C+∠ADC=360°,∠A=∠C,∠ABC=∠ADC,所以2∠A+
2∠ABC=360°.所以∠A+∠ABC=180°.所以AD∥BC.同理∠A+∠ADC=180°.所以AB∥CD.所以四边形ABCD是平行四边形.
(2)两组对角分别相等的四边形是平行四边形
(3)B
图2
A
C
O
D
B
图1
E
图3
S1
图4
图6图5
图8
图9
图7
图12
图11
A
B
C
D
图10
图15
E
B
C
D
A
F
O
C
F
D
E
B
A
图13
图14
图17
O
G
C
F
D
E
B
A
图16
