鲁教版数学九年级上册单元测试题_第四章投影与视图(含答案)
文档属性
| 名称 | 鲁教版数学九年级上册单元测试题_第四章投影与视图(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-13 00:00:00 | ||
图片预览

文档简介
第四章投影与视图
测试题
(时间:
满分:120分)
(班级:
姓名:
得分:
)
一、选择题(每小题3分,共30分)
1.平行投影中的光线是(
)
A.平行的
B
.聚成一点的
C.不平行的
D.向四面发散的
2.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是
(
)
A.相等
B.长的较长
C.短的较长
D.不能确定
3.正方形在太阳光的投影下得到的几何图形一定是
(
)
A.正方形
B.平行四边形或一条线段
C.矩形
D.菱形
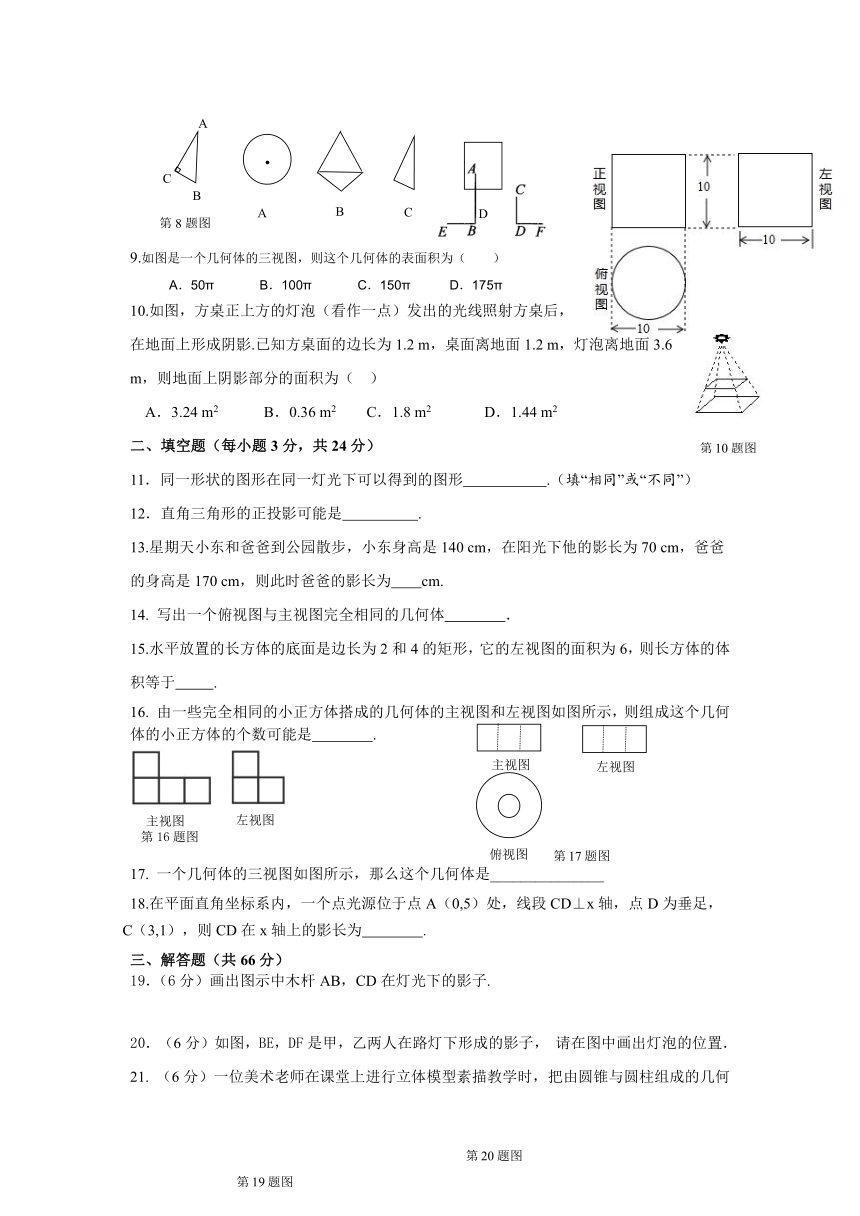
4.下列图中是太阳光下形成的影子的是
(
)
A
B
C
D
5.底面与投影面垂直的圆锥体的正投影是
(
)
A.圆
B.三角形
C.矩形
D.正方形
6.
如图,晚上小明在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子(
)
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
7.
如图是一个三棱柱的立体图形,它的俯视图是( )
A
B
C
D
8.将如图所示的Rt△ABC绕斜边AB所在的直线旋转一周,所得几何体的左视图是(
)
9.如图是一个几何体的三视图,则这个几何体的表面积为( )
A.50π
B.100π
C.150π
D.175π
10.如图,方桌正上方的灯泡(看作一点)发出的光线照射方桌后,在地面上形成阴影.已知方桌面的边长为1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为(
)
A.3.24
m2
B.0.36
m2
C.1.8
m2
D.1.44
m2
二、填空题(每小题3分,共24分)
11.同一形状的图形在同一灯光下可以得到的图形
.(填“相同”或“不同”)
12.直角三角形的正投影可能是
.
13.星期天小东和爸爸到公园散步,小东身高是140
cm,在阳光下他的影长为70
cm,爸爸
的身高是170
cm,则此时爸爸的影长为
cm.
14.
写出一个俯视图与主视图完全相同的几何体
.
15.水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于
.
16.
由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是
.
SHAPE
\
MERGEFORMAT
一个几何体的三视图如图所示,那么这个几何体是_______________
18.在平面直角坐标系内,一个点光源位于点A(0,5)处,线段CD⊥x轴,点D为垂足,
C(3,1),则CD在x轴上的影长为
.
三、解答题(共66分)
19.(6分)画出图示中木杆AB,CD在灯光下的影子.
20.(6分)如图,BE,DF是甲,乙两人在路灯下形成的影子,请在图中画出灯泡的位置.
21.
(6分)一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图.
22.(8分)一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的名称,并根据图中所给的数据求出它的侧面积.
23.
(8分)如图,在圆桌的正上方有一盏吊灯,在灯光下,圆桌在地板上的投影是面积为4m2的圆.已知圆桌的高度为1m,圆桌面的半径为0.5m,试求吊灯距圆桌面的距离.
第23题图
第24题图
24.(10分)在一次数学活动课上,李老师带领学生去测教学楼的高度.在阳光下,测得身高1.65米的黄丽同学BC的影长BA为1.1米,与此同时,测得教学楼DE的影长DF为12.1米,如图.
(1)请你在图中画出此时教学楼DE在阳光下的投影DF.
(2)请你根据已测得的数据,求出教学楼DE的高度(精确到0.1米).
25.(10分)如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,求两路灯之间的距离.
第25题图
26.
(12分)学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6
m的小明(AB)的影子BC长是3
m,而小颖(EH)刚好在路灯灯泡的正下方点H外,并测得HB=6
m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下路程的到B2处时,求其影子B2C2的长;当小明继续走剩下路程的到B3处,……按此规律继续走下去,当小明走剩下路程的到Bn处时,其影子BnCn的长(用含n的代数式表示).
第26题图
参考答案
一、1.A
2.D
3.B
4.A
5.B
6.C
7.A
8.B
9.C
10.A
二、11.不同
12.三角形或线段
13.
85
14.
球或正方体(答案不唯一)
15.24或12
16.4或5或6或7
17.空心圆柱
18.
三、19.略.
20.解:连接EA,FC,它们的延长线的交点即为灯泡的位置,图略.
21.解:如图所示.
22.解:该几何体是直四棱柱(答直棱柱,四棱柱,棱柱也正确).
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm.
所以菱形的边长为cm,棱柱的侧面积=×8×4=80(cm2).
23.m.
24.(1)如图,注意AC与EF平行.
(2)由,解得DE=18.15≈18.2.
所以教学楼DE的高度约为18.2米.
25.解:设AP=x,则BQ=x,AB=20+2x.由题意,得.解得x=5,AB=30.所以两路灯之间的距离是30m.
26.解:(1)如图①所示.
(2)由题意,得△ABC∽△GHC,所以
=,即=.
解得GH=4.8
m.故路灯灯泡的垂直高度GH为4.8
m.
(3)如图②.因为△A1B1C1∽△GHC1,所以
=.设B1C1的长为x,则=,解得x=,即B1C1=m.同理=,解得B2C2=1.由题意,得HBn=6×…=.所以=,所以=,解得BnCn=m.
第6题图
第7题图
A
C
B
B
A
C
D
第8题图
第10题图
主视图
俯视图
左视图
第17题图
主视图
左视图
第16题图
第20题图
第19题图
第21题图
主视图
左视图
俯视图
主视图
俯视图
左视图
第22题图
4cm
3cm
8cm
①
②
第26题图
测试题
(时间:
满分:120分)
(班级:
姓名:
得分:
)
一、选择题(每小题3分,共30分)
1.平行投影中的光线是(
)
A.平行的
B
.聚成一点的
C.不平行的
D.向四面发散的
2.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是
(
)
A.相等
B.长的较长
C.短的较长
D.不能确定
3.正方形在太阳光的投影下得到的几何图形一定是
(
)
A.正方形
B.平行四边形或一条线段
C.矩形
D.菱形
4.下列图中是太阳光下形成的影子的是
(
)
A
B
C
D
5.底面与投影面垂直的圆锥体的正投影是
(
)
A.圆
B.三角形
C.矩形
D.正方形
6.
如图,晚上小明在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子(
)
A.逐渐变短
B.逐渐变长
C.先变短后变长
D.先变长后变短
7.
如图是一个三棱柱的立体图形,它的俯视图是( )
A
B
C
D
8.将如图所示的Rt△ABC绕斜边AB所在的直线旋转一周,所得几何体的左视图是(
)
9.如图是一个几何体的三视图,则这个几何体的表面积为( )
A.50π
B.100π
C.150π
D.175π
10.如图,方桌正上方的灯泡(看作一点)发出的光线照射方桌后,在地面上形成阴影.已知方桌面的边长为1.2
m,桌面离地面1.2
m,灯泡离地面3.6
m,则地面上阴影部分的面积为(
)
A.3.24
m2
B.0.36
m2
C.1.8
m2
D.1.44
m2
二、填空题(每小题3分,共24分)
11.同一形状的图形在同一灯光下可以得到的图形
.(填“相同”或“不同”)
12.直角三角形的正投影可能是
.
13.星期天小东和爸爸到公园散步,小东身高是140
cm,在阳光下他的影长为70
cm,爸爸
的身高是170
cm,则此时爸爸的影长为
cm.
14.
写出一个俯视图与主视图完全相同的几何体
.
15.水平放置的长方体的底面是边长为2和4的矩形,它的左视图的面积为6,则长方体的体积等于
.
16.
由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示,则组成这个几何体的小正方体的个数可能是
.
SHAPE
\
MERGEFORMAT
一个几何体的三视图如图所示,那么这个几何体是_______________
18.在平面直角坐标系内,一个点光源位于点A(0,5)处,线段CD⊥x轴,点D为垂足,
C(3,1),则CD在x轴上的影长为
.
三、解答题(共66分)
19.(6分)画出图示中木杆AB,CD在灯光下的影子.
20.(6分)如图,BE,DF是甲,乙两人在路灯下形成的影子,请在图中画出灯泡的位置.
21.
(6分)一位美术老师在课堂上进行立体模型素描教学时,把由圆锥与圆柱组成的几何体(如图所示,圆锥在圆柱上底面正中间放置)摆在讲桌上,请你在指定的方框内分别画出这个几何体的三视图.
22.(8分)一个几何体的三视图如图所示,它的俯视图为菱形.请写出该几何体的名称,并根据图中所给的数据求出它的侧面积.
23.
(8分)如图,在圆桌的正上方有一盏吊灯,在灯光下,圆桌在地板上的投影是面积为4m2的圆.已知圆桌的高度为1m,圆桌面的半径为0.5m,试求吊灯距圆桌面的距离.
第23题图
第24题图
24.(10分)在一次数学活动课上,李老师带领学生去测教学楼的高度.在阳光下,测得身高1.65米的黄丽同学BC的影长BA为1.1米,与此同时,测得教学楼DE的影长DF为12.1米,如图.
(1)请你在图中画出此时教学楼DE在阳光下的投影DF.
(2)请你根据已测得的数据,求出教学楼DE的高度(精确到0.1米).
25.(10分)如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部.已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,求两路灯之间的距离.
第25题图
26.
(12分)学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时刻,身高为1.6
m的小明(AB)的影子BC长是3
m,而小颖(EH)刚好在路灯灯泡的正下方点H外,并测得HB=6
m.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G.
(2)求路灯灯泡的垂直高度GH.
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,求其影子B1C1的长;当小明继续走剩下路程的到B2处时,求其影子B2C2的长;当小明继续走剩下路程的到B3处,……按此规律继续走下去,当小明走剩下路程的到Bn处时,其影子BnCn的长(用含n的代数式表示).
第26题图
参考答案
一、1.A
2.D
3.B
4.A
5.B
6.C
7.A
8.B
9.C
10.A
二、11.不同
12.三角形或线段
13.
85
14.
球或正方体(答案不唯一)
15.24或12
16.4或5或6或7
17.空心圆柱
18.
三、19.略.
20.解:连接EA,FC,它们的延长线的交点即为灯泡的位置,图略.
21.解:如图所示.
22.解:该几何体是直四棱柱(答直棱柱,四棱柱,棱柱也正确).
由三视图知,棱柱底面菱形的对角线长分别为4cm,3cm.
所以菱形的边长为cm,棱柱的侧面积=×8×4=80(cm2).
23.m.
24.(1)如图,注意AC与EF平行.
(2)由,解得DE=18.15≈18.2.
所以教学楼DE的高度约为18.2米.
25.解:设AP=x,则BQ=x,AB=20+2x.由题意,得.解得x=5,AB=30.所以两路灯之间的距离是30m.
26.解:(1)如图①所示.
(2)由题意,得△ABC∽△GHC,所以
=,即=.
解得GH=4.8
m.故路灯灯泡的垂直高度GH为4.8
m.
(3)如图②.因为△A1B1C1∽△GHC1,所以
=.设B1C1的长为x,则=,解得x=,即B1C1=m.同理=,解得B2C2=1.由题意,得HBn=6×…=.所以=,所以=,解得BnCn=m.
第6题图
第7题图
A
C
B
B
A
C
D
第8题图
第10题图
主视图
俯视图
左视图
第17题图
主视图
左视图
第16题图
第20题图
第19题图
第21题图
主视图
左视图
俯视图
主视图
俯视图
左视图
第22题图
4cm
3cm
8cm
①
②
第26题图
