鲁教版数学七年级上册第二章轴对称综合测评
文档属性
| 名称 | 鲁教版数学七年级上册第二章轴对称综合测评 |  | |
| 格式 | zip | ||
| 文件大小 | 266.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-13 11:10:32 | ||
图片预览

文档简介
第二章
轴对称综合测评
时间:
分钟
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.
下列四个图形中,不是轴对称图形的是(
)
2.
正方形的对称轴的条数为(
)
A.1
B.2
C.3
D.4
3.在下面四个图形中,如果将左边的图形作轴对称折叠,能变成右边的图形的是(
)
4.
若等腰三角形的顶角为40°,则它的底角度数为( )
A.40° B.50° C.60° D.70°
5.
P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是(
)
A.OP1⊥OP2
B.OP1=OP2
C.OP1⊥OP2且OP1=OP2
D.OP1≠OP2
6.
下列说法中正确的是(
)
A.
关于一条直线对称的两个图形一定能重合
B.
两个能重合的图形一定关于某条直线对称
C.
一个轴对称图形只有一条对称轴
D.
轴对称图形的对应点一定在对称轴的两侧
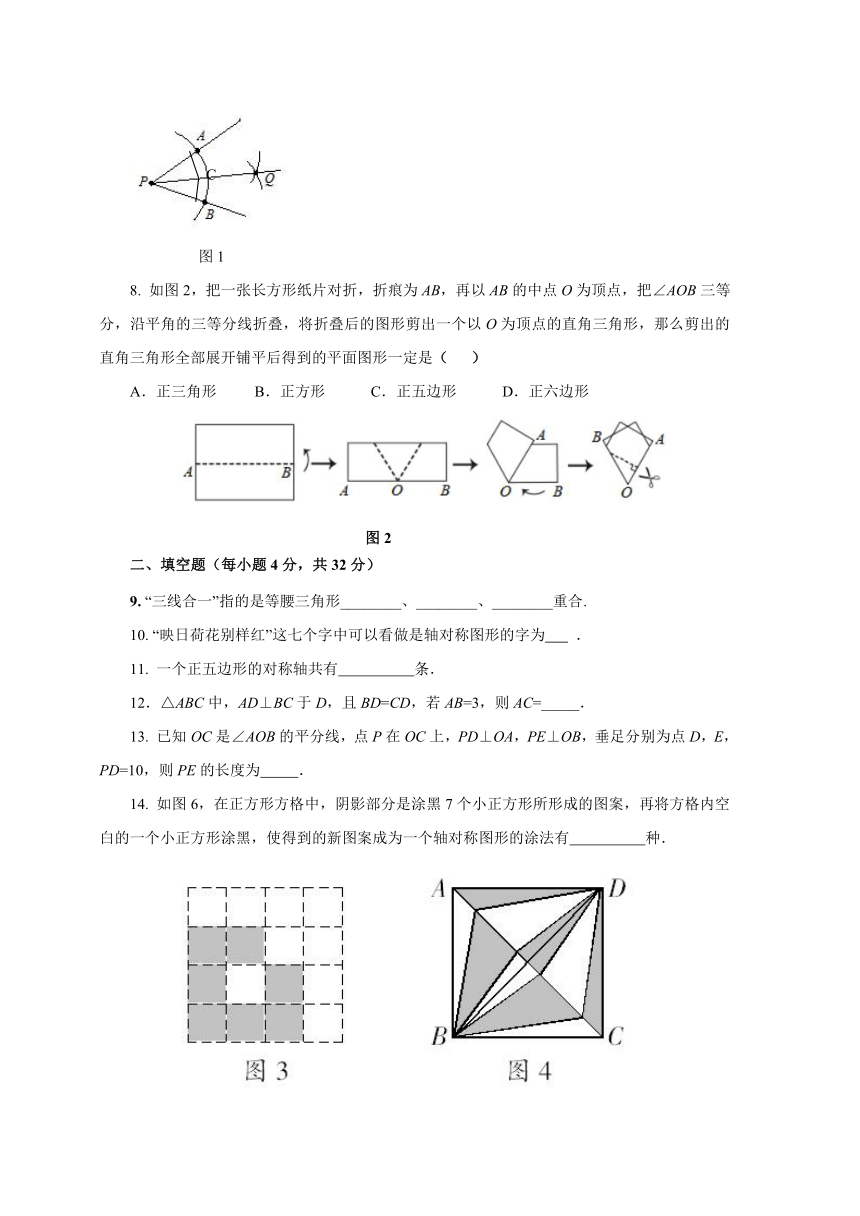
7.观察图1中尺规作图痕迹,下列结论错误的是(
)
A.PQ为∠APB的平分线
B.PA=PB
C.点A,B到PQ的距离不相等
D.AC
=BC
图1
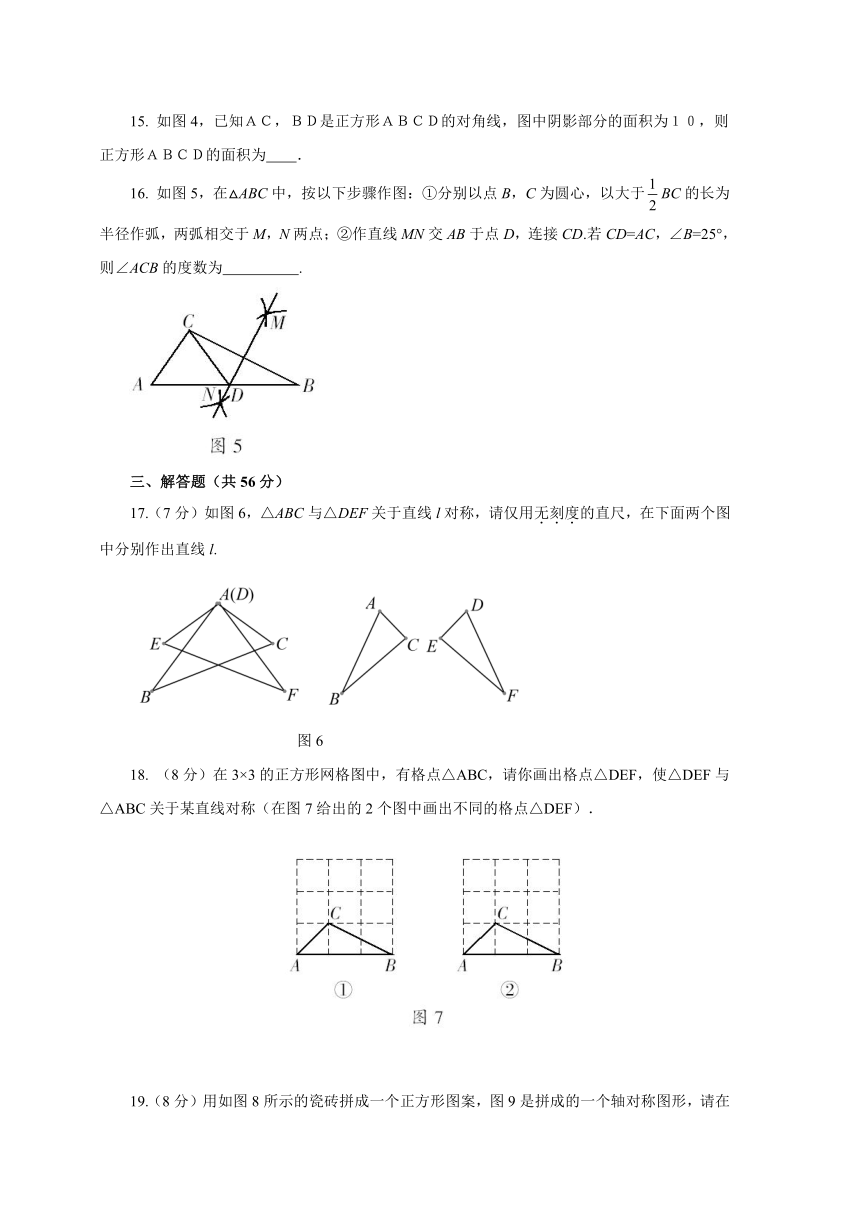
8.
如图2,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是(
)
A.正三角形
B.正方形
C.正五边形
D.正六边形
图2
二、填空题(每小题4分,共32分)
9.
“三线合一”指的是等腰三角形________、________、________重合.
10.
“映日荷花别样红”这七个字中可以看做是轴对称图形的字为
.
11.
一个正五边形的对称轴共有
条.
12.△ABC中,AD⊥BC于D,且BD=CD,若AB=3,则AC=_____.
13.
已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D,E,PD=10,则PE的长度为
.
14.
如图6,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有
种.
15.
如图4,已知AC,BD是正方形ABCD的对角线,图中阴影部分的面积为10,则正方形ABCD的面积为
.
16.
如图5,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为
.
三、解答题(共56分)
17.(7分)如图6,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
图6
18.
(8分)在3×3的正方形网格图中,有格点△ABC,请你画出格点△DEF,使△DEF与△ABC关于某直线对称(在图7给出的2个图中画出不同的格点△DEF).
19.(8分)用如图8所示的瓷砖拼成一个正方形图案,图9是拼成的一个轴对称图形,请在图10的两个空白的图中各给出一种不同的拼法,且均为轴对称图形.
20.(10分)如图11,在ΔABC中,AB=AC,D点在BC上,且BD=AD,DC=AC.将图中的等腰三角形全都写出来,并求∠B的度数.
21.(11分)如图12,把一张长方形纸片ABCD沿GH折叠,使点B与点D重合,其中AD∥BC,BD=10
cm,∠DGH=55°.
(1)求DF的长;
(2)求∠DHG的度数.
22.(12分)如图13,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法);
(2)连接BD,
BD平分∠CBA吗?为什么?
参考答案
一、1.
D
2.
D
3.
B
4.
D
5.
B
6.
A
7.
C
8.
A
二、9.
底边上的中线
底边上的高
顶角的平分线
10.
日
11.
5
12.
3
13.
10
14.
3
15.
20
16.
105°
三、17.
解:在图1中,过点A和BC,EF的交点作直线l;
在图2中,过BC,EF延长线的交点和AC,DF延长线的交点作直线l.
18.
答案不唯一,给出2种供参考,如图3所示.
19.
答案不唯一,如图4所示.
20.
解:△ABD,△ACD,△ABC均为等腰三角形.
设∠B=x°,因为△ABD是等腰三角形,所以∠BAD=∠B=x°.
所以∠ADB=180°-∠BAD-∠B=180°-2x°,所以∠ADC=180°-∠ADB=2x°.
因为△ABC为等腰三角形,所以∠C=∠B=x°.
因为△ACD为等腰三角形,所以∠CAD=∠ADC=2x°.
因为∠B+∠C+∠BAC=180°,所以x+x+3x=180,所以x=36.
所以∠B的度数为36°.
21.
解:(1)由题意可知四边形ABHG与四边形EDHG关于直线GH成轴对称,且点B与点D是一对对应点,所以GH垂直平分BD,所以DF=BD=5
cm.
(2)因为AD∥BC,所以∠BHG=∠DGH=55°.
因为四边形ABHG与四边形EDHG关于直线GH成轴对称,所以∠DHG=∠BHG=55°.
22.
解:(1)如图5所示,DE就是要求作的AB边的垂直平分线.
(2)如图6所示,BD平分∠CBA.理由如下:
因为DE是AB边的垂直平分线,所以AD=DB,所以△ABD是等腰三角形,所以∠ABD=∠A.
又因为∠A=30°,所以∠ABD=30°.
因为∠C=90°,所以∠ABC=90°-∠A=90°-30°=60°.
所以∠CBD=∠ABC-∠ABD=60°-30°=30°.
所以∠ABD=∠CBD,即BD平分∠CBA.
C
图8
图9
图10
图11
图13
轴对称综合测评
时间:
分钟
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.
下列四个图形中,不是轴对称图形的是(
)
2.
正方形的对称轴的条数为(
)
A.1
B.2
C.3
D.4
3.在下面四个图形中,如果将左边的图形作轴对称折叠,能变成右边的图形的是(
)
4.
若等腰三角形的顶角为40°,则它的底角度数为( )
A.40° B.50° C.60° D.70°
5.
P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是(
)
A.OP1⊥OP2
B.OP1=OP2
C.OP1⊥OP2且OP1=OP2
D.OP1≠OP2
6.
下列说法中正确的是(
)
A.
关于一条直线对称的两个图形一定能重合
B.
两个能重合的图形一定关于某条直线对称
C.
一个轴对称图形只有一条对称轴
D.
轴对称图形的对应点一定在对称轴的两侧
7.观察图1中尺规作图痕迹,下列结论错误的是(
)
A.PQ为∠APB的平分线
B.PA=PB
C.点A,B到PQ的距离不相等
D.AC
=BC
图1
8.
如图2,把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是(
)
A.正三角形
B.正方形
C.正五边形
D.正六边形
图2
二、填空题(每小题4分,共32分)
9.
“三线合一”指的是等腰三角形________、________、________重合.
10.
“映日荷花别样红”这七个字中可以看做是轴对称图形的字为
.
11.
一个正五边形的对称轴共有
条.
12.△ABC中,AD⊥BC于D,且BD=CD,若AB=3,则AC=_____.
13.
已知OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别为点D,E,PD=10,则PE的长度为
.
14.
如图6,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有
种.
15.
如图4,已知AC,BD是正方形ABCD的对角线,图中阴影部分的面积为10,则正方形ABCD的面积为
.
16.
如图5,在△ABC中,按以下步骤作图:①分别以点B,C为圆心,以大于BC的长为半径作弧,两弧相交于M,N两点;②作直线MN交AB于点D,连接CD.若CD=AC,∠B=25°,则∠ACB的度数为
.
三、解答题(共56分)
17.(7分)如图6,△ABC与△DEF关于直线l对称,请仅用无刻度的直尺,在下面两个图中分别作出直线l.
图6
18.
(8分)在3×3的正方形网格图中,有格点△ABC,请你画出格点△DEF,使△DEF与△ABC关于某直线对称(在图7给出的2个图中画出不同的格点△DEF).
19.(8分)用如图8所示的瓷砖拼成一个正方形图案,图9是拼成的一个轴对称图形,请在图10的两个空白的图中各给出一种不同的拼法,且均为轴对称图形.
20.(10分)如图11,在ΔABC中,AB=AC,D点在BC上,且BD=AD,DC=AC.将图中的等腰三角形全都写出来,并求∠B的度数.
21.(11分)如图12,把一张长方形纸片ABCD沿GH折叠,使点B与点D重合,其中AD∥BC,BD=10
cm,∠DGH=55°.
(1)求DF的长;
(2)求∠DHG的度数.
22.(12分)如图13,△ABC中,∠C=90°,∠A=30°.
(1)用尺规作图作AB边的垂直平分线DE,交AC于点D,交AB于点E.(保留作图痕迹,不要求写作法);
(2)连接BD,
BD平分∠CBA吗?为什么?
参考答案
一、1.
D
2.
D
3.
B
4.
D
5.
B
6.
A
7.
C
8.
A
二、9.
底边上的中线
底边上的高
顶角的平分线
10.
日
11.
5
12.
3
13.
10
14.
3
15.
20
16.
105°
三、17.
解:在图1中,过点A和BC,EF的交点作直线l;
在图2中,过BC,EF延长线的交点和AC,DF延长线的交点作直线l.
18.
答案不唯一,给出2种供参考,如图3所示.
19.
答案不唯一,如图4所示.
20.
解:△ABD,△ACD,△ABC均为等腰三角形.
设∠B=x°,因为△ABD是等腰三角形,所以∠BAD=∠B=x°.
所以∠ADB=180°-∠BAD-∠B=180°-2x°,所以∠ADC=180°-∠ADB=2x°.
因为△ABC为等腰三角形,所以∠C=∠B=x°.
因为△ACD为等腰三角形,所以∠CAD=∠ADC=2x°.
因为∠B+∠C+∠BAC=180°,所以x+x+3x=180,所以x=36.
所以∠B的度数为36°.
21.
解:(1)由题意可知四边形ABHG与四边形EDHG关于直线GH成轴对称,且点B与点D是一对对应点,所以GH垂直平分BD,所以DF=BD=5
cm.
(2)因为AD∥BC,所以∠BHG=∠DGH=55°.
因为四边形ABHG与四边形EDHG关于直线GH成轴对称,所以∠DHG=∠BHG=55°.
22.
解:(1)如图5所示,DE就是要求作的AB边的垂直平分线.
(2)如图6所示,BD平分∠CBA.理由如下:
因为DE是AB边的垂直平分线,所以AD=DB,所以△ABD是等腰三角形,所以∠ABD=∠A.
又因为∠A=30°,所以∠ABD=30°.
因为∠C=90°,所以∠ABC=90°-∠A=90°-30°=60°.
所以∠CBD=∠ABC-∠ABD=60°-30°=30°.
所以∠ABD=∠CBD,即BD平分∠CBA.
C
图8
图9
图10
图11
图13
