鲁教版数学七年级上册第一章 三角形综合测评试卷
文档属性
| 名称 | 鲁教版数学七年级上册第一章 三角形综合测评试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-13 11:12:54 | ||
图片预览

文档简介
三角形综合测评
时间:
分钟
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.已知三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能是
(
)
A.1cm
B.2cm
C.7cm
D.10cm
在△ABC中,若∠A+∠B<∠C,则三角形为
(
)
锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
下列说法不正确的是
(
)
三角形的三条中线交于三角形内一点
三角形的三条角平分线交于三角形内一点
三角形的三条高交于三角形内一点
三角形的中线、角平分线和高都是线段
在同一平面内有4个点,且任意三点都不在同一条直线上,以其中三点为三角形的顶点可作出所有三角形的个数为
(
)
A.4
B.6
C.7
D.8
已知△ABC≌△DEF,AB=4cm,AC=6cm,DE+EF=9cm,则EF的长为
(
)
A.3cm
B.4cm
C.5cm
D.6cm
如图1,已知BD平分∠ABC,DE⊥AB,DF⊥BC,则下列结论不正确的是
(
)
AD=CD
B.DE=DF
C.BE=BF
D.∠BDE=∠BDF
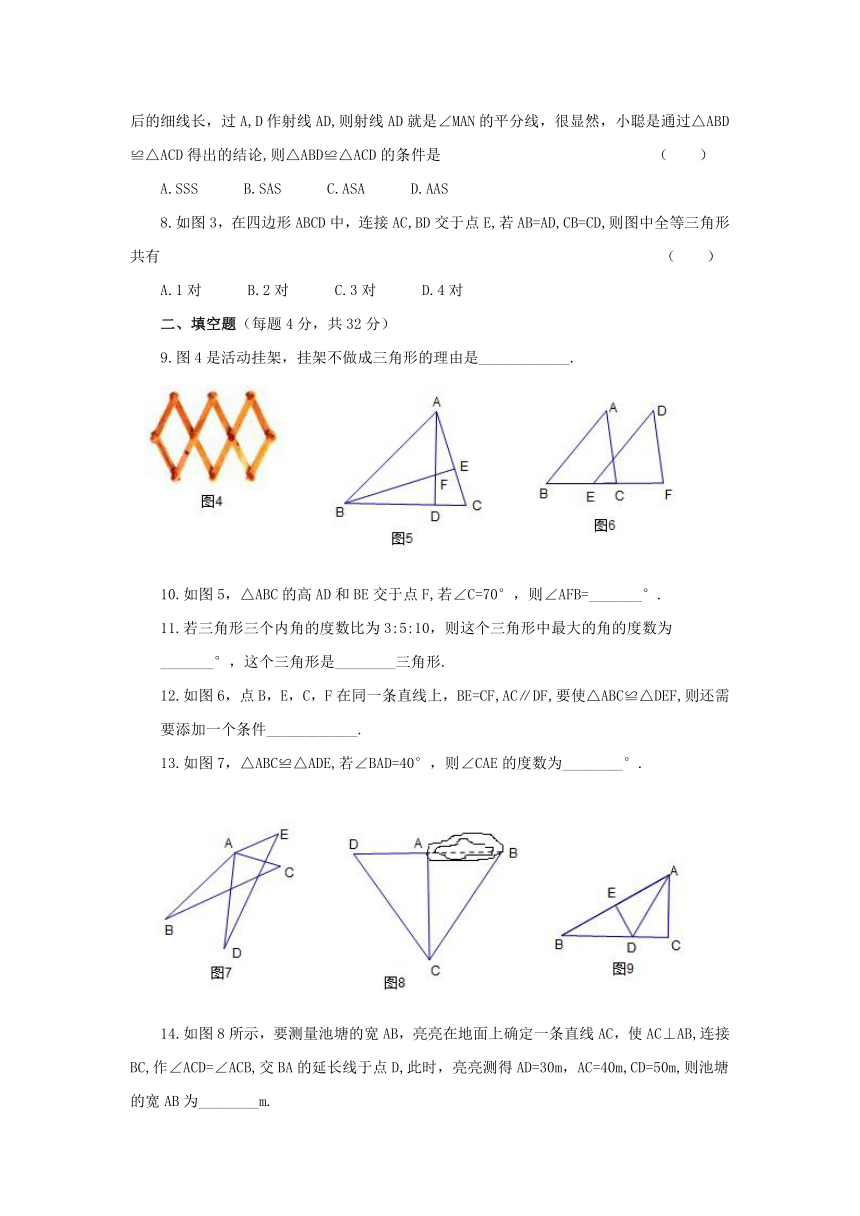
如图2,小聪想作∠MAN的平分线,但手边仅有一条细线,于是他用细线量取AB=AC,然后截取一段长为BC的细线,将截得的细线对折,再在线段BC上量取BD,使BD等于对折后的细线长,过A,D作射线AD,则射线AD就是∠MAN的平分线,很显然,小聪是通过△ABD≌△ACD得出的结论,则△ABD≌△ACD的条件是
(
)
SSS
B.SAS
C.ASA
D.AAS
如图3,在四边形ABCD中,连接AC,BD交于点E,若AB=AD,CB=CD,则图中全等三角形共有
(
)
A.1对
B.2对
C.3对
D.4对
二、填空题(每题4分,共32分)
9.图4是活动挂架,挂架不做成三角形的理由是____________.
10.如图5,△ABC的高AD和BE交于点F,若∠C=70°,则∠AFB=_______°.
11.若三角形三个内角的度数比为3:5:10,则这个三角形中最大的角的度数为_______°,这个三角形是________三角形.
12.如图6,点B,E,C,F在同一条直线上,BE=CF,AC∥DF,要使△ABC≌△DEF,则还需要添加一个条件____________.
13.如图7,△ABC≌△ADE,若∠BAD=40°,则∠CAE的度数为________°.
14.如图8所示,要测量池塘的宽AB,亮亮在地面上确定一条直线AC,使AC⊥AB,连接BC,作∠ACD=∠ACB,交BA的延长线于点D,此时,亮亮测得AD=30m,AC=40m,CD=50m,则池塘的宽AB为________m.
15.若等腰三角形的底边长为10cm,腰长为偶数,则满足条件的腰长的最小值为____cm.
16.如图9,在△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,DE⊥AB于E,有下列结论:①DE=DC;②∠BDE=∠ADC;③AB=2AC;④图中共有两对全等三角形.其中正确的是:____________(填序号即可).
三、解答题(共56分)
17.(8分)在△ABC中,∠B比∠A的4倍少10°,∠C比∠A的4倍多10°,你知道△ABC是什么三角形吗?请你简单说明理由.
18.(9分)如图10,在△ABC中,D为AC的中点,F为AB上任意一点,CE∥AB,CE与直线DF交于点E,问:△ADF与△CDE全等吗?请说明理由.
19.(9分)如图11,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌
△CDE,AB=6,BC=8,CE=10.
求△ABC的周长;
求△ACE的面积.
(9分)如图12,已知线段AB,利用尺规作图,作出一个以线段AB为边的等边三角形ABC.(保留作图痕迹,不写作法)
(9分)仔细阅读下面的解题过程,并完成填空:
如图13,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.
解:延长AD到E,使DE
=
AD,连接BE.
因为AD为△ABC的中线,
所以BD=CD.
在△ACD和△EBD中,因为AD=DE,∠ADC=∠EDB,CD=BD,所以△ACD≌△EBD(__________).
所以BE=AC(_____________________).
因为AB+BE>AE(_____________________),
所以AB+AC>AE.
因为AE=2AD=8cm,
所以AB+AC>_______cm.
(12分)如图14,已知△ABC≌△BAD,AD与BC交于点E,试说明△ABE是等腰三角形.
参考答案
一、1.C
2.
C
3.C
4.A
5.C
6.A
7.A
8.C
二、9.三角形具有稳定性
10.110
11.100
钝角
12.答案不唯一,如AC=DF等
13.40
14.30
15.6
16.①②③
三、17.解:直角三角形.理由如下:
设∠A=x,则∠B=4x-10,∠C=4x+10,由三角形内角和为180°,得x+4x-10+4x+10=180.
解方程,得x=20.
所以4x+10=90.
所以∠C=90°.
所以△ABC是直角三角形.
解:△ADF≌△CDE.理由如下:
因为CE∥AB,所以∠A=∠DCE.
因为D为AC的中点,所以AD=CD.
又因为∠ADF=∠CDE,所以△ADF≌△CDE.
解:(1)因为△ABC≌△CDE,所以AC=CE=10.
所以△ABC的周长为AB+BC+AC=6+8+10=24.
因为△ABC≌△CDE,所以∠ACB=∠CED,AC=CE=10.
因为∠CED+∠ECD=90°,所以∠ACB+∠ECD=90°.
所以∠ACE=90°.
所以S△ACE=AC·CE=×10×10=50.
20.
解:如图所示:
21.
解:依次填SAS
全等三角形对应边相等
三角形两边之和大于第三边
8
解:因为△ABC≌△BAD,所以∠C=∠D,AC=BD.
又因为∠AEC=∠BED,所以△AEC≌△BED.
所以AE=BE.
所以△ABE是等腰三角形.
时间:
分钟
满分:120分
班级:
姓名:
得分:
一、选择题(每小题4分,共32分)
1.已知三角形的两边长分别为3cm和5cm,则此三角形的第三边长可能是
(
)
A.1cm
B.2cm
C.7cm
D.10cm
在△ABC中,若∠A+∠B<∠C,则三角形为
(
)
锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
下列说法不正确的是
(
)
三角形的三条中线交于三角形内一点
三角形的三条角平分线交于三角形内一点
三角形的三条高交于三角形内一点
三角形的中线、角平分线和高都是线段
在同一平面内有4个点,且任意三点都不在同一条直线上,以其中三点为三角形的顶点可作出所有三角形的个数为
(
)
A.4
B.6
C.7
D.8
已知△ABC≌△DEF,AB=4cm,AC=6cm,DE+EF=9cm,则EF的长为
(
)
A.3cm
B.4cm
C.5cm
D.6cm
如图1,已知BD平分∠ABC,DE⊥AB,DF⊥BC,则下列结论不正确的是
(
)
AD=CD
B.DE=DF
C.BE=BF
D.∠BDE=∠BDF
如图2,小聪想作∠MAN的平分线,但手边仅有一条细线,于是他用细线量取AB=AC,然后截取一段长为BC的细线,将截得的细线对折,再在线段BC上量取BD,使BD等于对折后的细线长,过A,D作射线AD,则射线AD就是∠MAN的平分线,很显然,小聪是通过△ABD≌△ACD得出的结论,则△ABD≌△ACD的条件是
(
)
SSS
B.SAS
C.ASA
D.AAS
如图3,在四边形ABCD中,连接AC,BD交于点E,若AB=AD,CB=CD,则图中全等三角形共有
(
)
A.1对
B.2对
C.3对
D.4对
二、填空题(每题4分,共32分)
9.图4是活动挂架,挂架不做成三角形的理由是____________.
10.如图5,△ABC的高AD和BE交于点F,若∠C=70°,则∠AFB=_______°.
11.若三角形三个内角的度数比为3:5:10,则这个三角形中最大的角的度数为_______°,这个三角形是________三角形.
12.如图6,点B,E,C,F在同一条直线上,BE=CF,AC∥DF,要使△ABC≌△DEF,则还需要添加一个条件____________.
13.如图7,△ABC≌△ADE,若∠BAD=40°,则∠CAE的度数为________°.
14.如图8所示,要测量池塘的宽AB,亮亮在地面上确定一条直线AC,使AC⊥AB,连接BC,作∠ACD=∠ACB,交BA的延长线于点D,此时,亮亮测得AD=30m,AC=40m,CD=50m,则池塘的宽AB为________m.
15.若等腰三角形的底边长为10cm,腰长为偶数,则满足条件的腰长的最小值为____cm.
16.如图9,在△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,DE⊥AB于E,有下列结论:①DE=DC;②∠BDE=∠ADC;③AB=2AC;④图中共有两对全等三角形.其中正确的是:____________(填序号即可).
三、解答题(共56分)
17.(8分)在△ABC中,∠B比∠A的4倍少10°,∠C比∠A的4倍多10°,你知道△ABC是什么三角形吗?请你简单说明理由.
18.(9分)如图10,在△ABC中,D为AC的中点,F为AB上任意一点,CE∥AB,CE与直线DF交于点E,问:△ADF与△CDE全等吗?请说明理由.
19.(9分)如图11,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌
△CDE,AB=6,BC=8,CE=10.
求△ABC的周长;
求△ACE的面积.
(9分)如图12,已知线段AB,利用尺规作图,作出一个以线段AB为边的等边三角形ABC.(保留作图痕迹,不写作法)
(9分)仔细阅读下面的解题过程,并完成填空:
如图13,AD为△ABC的中线,已知AD=4cm,试确定AB+AC的取值范围.
解:延长AD到E,使DE
=
AD,连接BE.
因为AD为△ABC的中线,
所以BD=CD.
在△ACD和△EBD中,因为AD=DE,∠ADC=∠EDB,CD=BD,所以△ACD≌△EBD(__________).
所以BE=AC(_____________________).
因为AB+BE>AE(_____________________),
所以AB+AC>AE.
因为AE=2AD=8cm,
所以AB+AC>_______cm.
(12分)如图14,已知△ABC≌△BAD,AD与BC交于点E,试说明△ABE是等腰三角形.
参考答案
一、1.C
2.
C
3.C
4.A
5.C
6.A
7.A
8.C
二、9.三角形具有稳定性
10.110
11.100
钝角
12.答案不唯一,如AC=DF等
13.40
14.30
15.6
16.①②③
三、17.解:直角三角形.理由如下:
设∠A=x,则∠B=4x-10,∠C=4x+10,由三角形内角和为180°,得x+4x-10+4x+10=180.
解方程,得x=20.
所以4x+10=90.
所以∠C=90°.
所以△ABC是直角三角形.
解:△ADF≌△CDE.理由如下:
因为CE∥AB,所以∠A=∠DCE.
因为D为AC的中点,所以AD=CD.
又因为∠ADF=∠CDE,所以△ADF≌△CDE.
解:(1)因为△ABC≌△CDE,所以AC=CE=10.
所以△ABC的周长为AB+BC+AC=6+8+10=24.
因为△ABC≌△CDE,所以∠ACB=∠CED,AC=CE=10.
因为∠CED+∠ECD=90°,所以∠ACB+∠ECD=90°.
所以∠ACE=90°.
所以S△ACE=AC·CE=×10×10=50.
20.
解:如图所示:
21.
解:依次填SAS
全等三角形对应边相等
三角形两边之和大于第三边
8
解:因为△ABC≌△BAD,所以∠C=∠D,AC=BD.
又因为∠AEC=∠BED,所以△AEC≌△BED.
所以AE=BE.
所以△ABE是等腰三角形.
