13.2.1 作轴对称图形教案(第二课时,表格形式)
文档属性
| 名称 | 13.2.1 作轴对称图形教案(第二课时,表格形式) |
|
|
| 格式 | zip | ||
| 文件大小 | 395.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-14 00:00:00 | ||
图片预览

文档简介
授课计划
课题名称
第5课时
作轴对称图形(2)
课时安排
1
教学目标
1.能够按要求作出简单平面图形经过轴对称后的图形.2.培养学生运用轴对称解决实际问题的基本能力.3.使学生掌握数学知识的衔接与各部分知识间的相互联系.
教学重点
能够按要求作出简单平面图形经过轴对称后的图形
教学难点
应用轴对称解决实际问题.
教法学法
自主探究,小组合作
教具
ppt课件
教
学
过
程
教学环节
教学活动
一、创设情境
导入新课二、合作交流
解读探究三、应用迁移
巩固提高
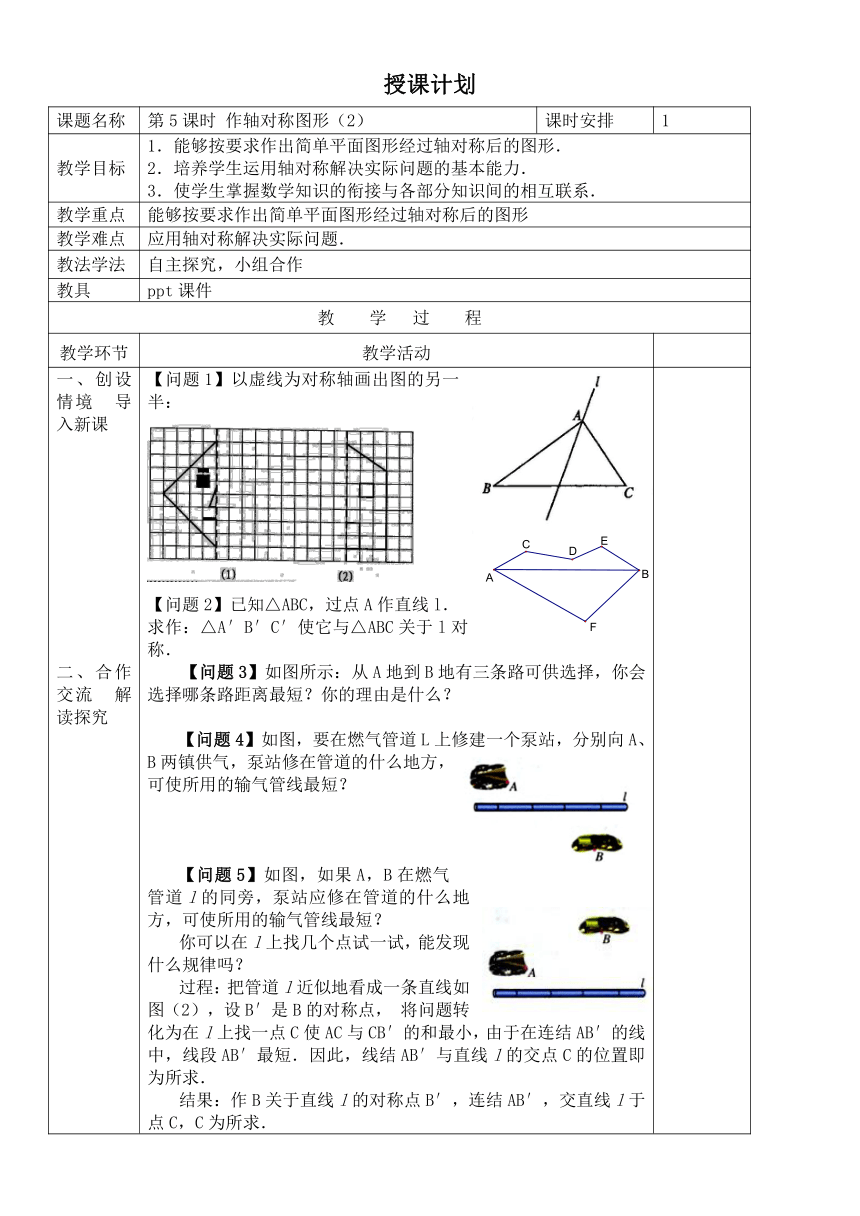
【问题1】以虚线为对称轴画出图的另一半:
( http: / / www.21cnjy.com )【问题2】已知△ABC,过点A作直线l.求作:△A′B′C′使它与△ABC关于l对称.【问题3】如图所示:从A地到B地有三条路可供选择,你会选择哪条路距离最短?你的理由是什么?【问题4】如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?【问题5】如图,如果A,B在燃气管道l的同旁,泵站应修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律吗?过程:把管道l近似地看成一条直线如图(2
( http: / / www.21cnjy.com )),设B′是B的对称点,将问题转化为在l上找一点C使AC与CB′的和最小,由于在连结AB′的线中,线段AB′最短.因此,线结AB′与直线l的交点C的位置即为所求.结果:作B关于直线l的对称点B′,连结AB′,交直线l于点C,C为所求.【思考】为什么在点C的位置修建泵站,就能使所用的输管道最短?过程:将实际问题转化为数学问题,该问题就是证明AC+CB最小.结果:如上图,在直线l上取不同于点C的任意一点C
( http: / / www.21cnjy.com )′.由于B′点是B点关于L的对称点,所以BC′=B′C′,故AC′+BC′=AC′+B′C′,在△A′B′C′中AC′+BC′>AB′,而AB′=AC+CB′=AC+CB,则有AC+CB【例1】八年级某班同学做游戏,在活动区域边放了一些球,则小明按怎样的路线跑,去捡哪个位置的球,才能最短的距离拿到球并跑到目的地A处。【例2】在例1中,如果另一侧放着一些小木棍
( http: / / www.21cnjy.com ),小明先去捡球,还要跑到另一侧去取木棍,则小明又应按怎样的路线跑,去捡哪个位置的球,小木棍,才能最快跑到目的地A处。【例3】如图,A为马厩,B
( http: / / www.21cnjy.com )为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
板书设计
( http: / / www.21cnjy.com )
作业布置
练习册
预习内容
第6课时
用坐标表示轴对称
课后反思
作某点使距离之和最小的问题学生都能很快地解决,但是还是没有明白为什么应这样作图,反映出了“知其然,不知其所以然”。
课题名称
第5课时
作轴对称图形(2)
课时安排
1
教学目标
1.能够按要求作出简单平面图形经过轴对称后的图形.2.培养学生运用轴对称解决实际问题的基本能力.3.使学生掌握数学知识的衔接与各部分知识间的相互联系.
教学重点
能够按要求作出简单平面图形经过轴对称后的图形
教学难点
应用轴对称解决实际问题.
教法学法
自主探究,小组合作
教具
ppt课件
教
学
过
程
教学环节
教学活动
一、创设情境
导入新课二、合作交流
解读探究三、应用迁移
巩固提高
【问题1】以虚线为对称轴画出图的另一半:
( http: / / www.21cnjy.com )【问题2】已知△ABC,过点A作直线l.求作:△A′B′C′使它与△ABC关于l对称.【问题3】如图所示:从A地到B地有三条路可供选择,你会选择哪条路距离最短?你的理由是什么?【问题4】如图,要在燃气管道L上修建一个泵站,分别向A、B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?【问题5】如图,如果A,B在燃气管道l的同旁,泵站应修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律吗?过程:把管道l近似地看成一条直线如图(2
( http: / / www.21cnjy.com )),设B′是B的对称点,将问题转化为在l上找一点C使AC与CB′的和最小,由于在连结AB′的线中,线段AB′最短.因此,线结AB′与直线l的交点C的位置即为所求.结果:作B关于直线l的对称点B′,连结AB′,交直线l于点C,C为所求.【思考】为什么在点C的位置修建泵站,就能使所用的输管道最短?过程:将实际问题转化为数学问题,该问题就是证明AC+CB最小.结果:如上图,在直线l上取不同于点C的任意一点C
( http: / / www.21cnjy.com )′.由于B′点是B点关于L的对称点,所以BC′=B′C′,故AC′+BC′=AC′+B′C′,在△A′B′C′中AC′+BC′>AB′,而AB′=AC+CB′=AC+CB,则有AC+CB
( http: / / www.21cnjy.com ),小明先去捡球,还要跑到另一侧去取木棍,则小明又应按怎样的路线跑,去捡哪个位置的球,小木棍,才能最快跑到目的地A处。【例3】如图,A为马厩,B
( http: / / www.21cnjy.com )为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
板书设计
( http: / / www.21cnjy.com )
作业布置
练习册
预习内容
第6课时
用坐标表示轴对称
课后反思
作某点使距离之和最小的问题学生都能很快地解决,但是还是没有明白为什么应这样作图,反映出了“知其然,不知其所以然”。
