13.2.2 用坐标表示轴对称教案
图片预览
文档简介
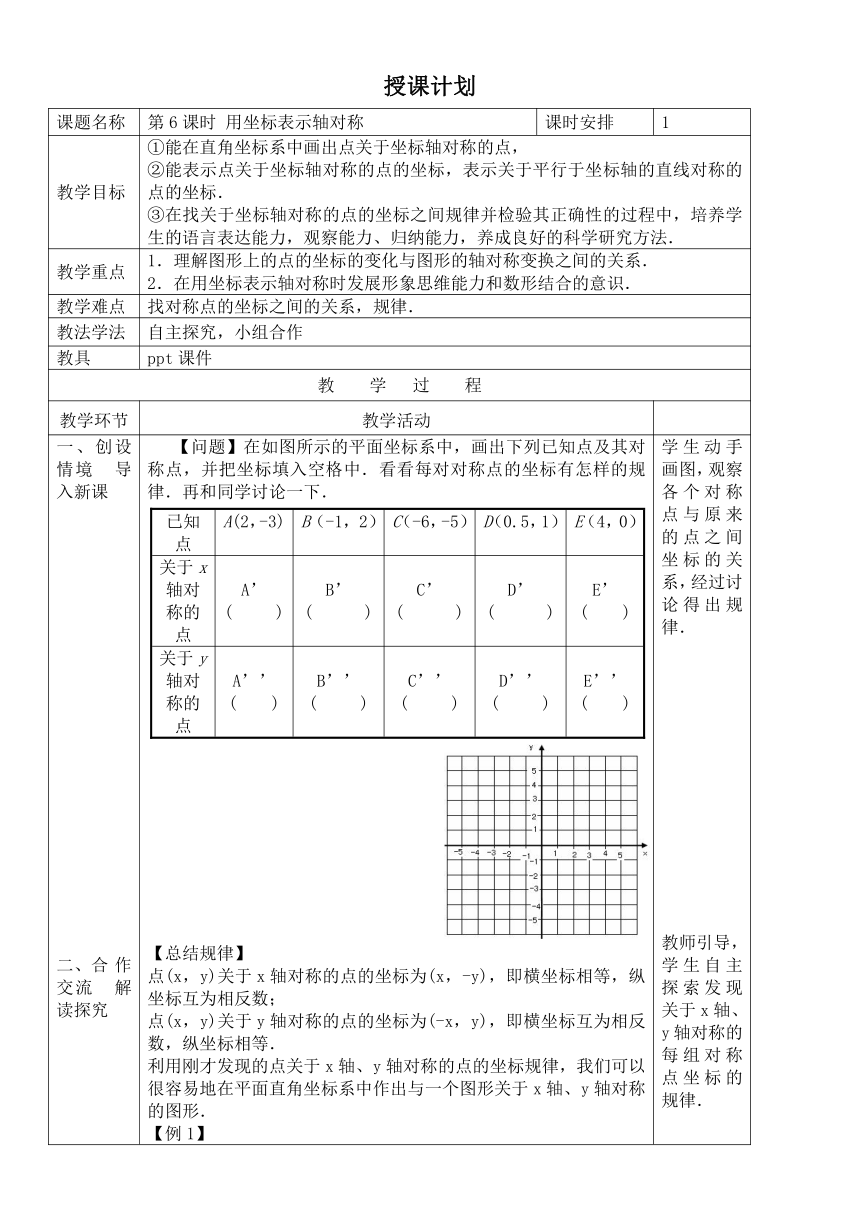
授课计划
课题名称
第6课时
用坐标表示轴对称
课时安排
1
教学目标
①能在直角坐标系中画出点关于坐标轴对称的点,②能表示点关于坐标轴对称的点的坐标,表示关于平行于坐标轴的直线对称的点的坐标.③在找关于坐标轴对称的点的坐标之间规律并检验其正确性的过程中,培养学生的语言表达能力,观察能力、归纳能力,养成良好的科学研究方法.
教学重点
1.理解图形上的点的坐标的变化与图形的轴对称变换之间的关系.2.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
教学难点
找对称点的坐标之间的关系,规律.
教法学法
自主探究,小组合作
教具
ppt课件
教
学
过
程
教学环节
教学活动
一、创设情境
导入新课合作交流
解读探究三、应用迁移
巩固提高四、总结反思
拓展升华
【问题】在如图所示的平面坐标系中,画出下列已知点及其对称点,并把坐标填入空格中.看看每对对称点的坐标有怎样的规律.再和同学讨论一下.已知点A(2,-3)B(-1,2)C(-6,-5)D(0.5,1)E(4,0)关于x轴对称的点A’(
)B’(
)C’(
)D’(
)E’(
)关于y轴对称的点A’’(
)B’’(
)C’’(
)D’’(
)E’’(
)【总结规律】点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标相等,纵坐标互为相反数;点(x,y)关于y轴对称的点的坐标为(-x,y),即横坐标互为相反数,纵坐标相等.利用刚才发现的点关于x轴、y轴对称的点的坐标规律,我们可以很容易地在平面直角坐标系中作出与一个图形关于x轴、y轴对称的图形.【例1】①点P(-5,
6)与点Q关于x轴对称,则点Q的坐标为__________.②点M
(a,
-5)与点N(-2,
b)关于x轴对称,则a=_____,
b
=_____.③点P(-5,
6)与点Q关于y轴对称,则点Q的坐标为__________.④点M
(a,
-5)与点N(-2,
b)关于y轴对称,则a=_____,
b
=_____.⑤已知点P(2a+b,-3a)与点P’(8,b+2).若点p与点p’关于x轴对称,则a=_____
b=_______.若点p与点p’关于y轴对称,则a=_____
b=_______.【例2】如图,利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于x轴和y轴对称的图形。
( http: / / www.21cnjy.com )【例3】如下图,四边形ABCD的四个顶点
( http: / / www.21cnjy.com )的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别作出四边形ABCD关于y轴和x轴对称的图形。
( http: / / www.21cnjy.com )【练习】课本Р45
练习21.点关于某条直线对称的点的坐标可以通过寻找线段之间的关系来求.2、(x,y)关于x轴对称的点的坐标为(x
( http: / / www.21cnjy.com ),-y),即横坐标相等,纵坐标互为相反数;点(x,y)关于y轴对称的点的坐标为(-x,y),即横坐标互为相反数,纵坐标相等.3、如果作关于直线x=3(记为m)和直线y=-4(记为n)对称的图形,你能发现对应点的坐标之间的关系吗
学生动手画图,观察各个对称点与原来的点之间坐标的关系,经过讨论得出规律.教师引导,学生自主探索发现关于x轴、y轴对称的每组对称点坐标的规律.直接应用关于x、y轴对称点的坐标特征得出结果。学生根据关于x、y轴对称点的坐标特征,首先求出各点关于x轴、y轴的对称点,然后再连接对称点即可.本活动主要巩固加深学生对利用坐标表示轴对称的理解,所以要特别关注学生对对称点的坐标的求解过程.
板书设计
( http: / / www.21cnjy.com )
作业布置
P71
预习内容
第7课时
等腰三角形(1)
课后反思
利用坐标特征进行数学应用,是初一已经学过的
( http: / / www.21cnjy.com ),这里方程思想和数形结合思想必须继续训练,放手由学生进行自我训练、自我评价,感觉在学生评价上力度还需更加大些。
课题名称
第6课时
用坐标表示轴对称
课时安排
1
教学目标
①能在直角坐标系中画出点关于坐标轴对称的点,②能表示点关于坐标轴对称的点的坐标,表示关于平行于坐标轴的直线对称的点的坐标.③在找关于坐标轴对称的点的坐标之间规律并检验其正确性的过程中,培养学生的语言表达能力,观察能力、归纳能力,养成良好的科学研究方法.
教学重点
1.理解图形上的点的坐标的变化与图形的轴对称变换之间的关系.2.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
教学难点
找对称点的坐标之间的关系,规律.
教法学法
自主探究,小组合作
教具
ppt课件
教
学
过
程
教学环节
教学活动
一、创设情境
导入新课合作交流
解读探究三、应用迁移
巩固提高四、总结反思
拓展升华
【问题】在如图所示的平面坐标系中,画出下列已知点及其对称点,并把坐标填入空格中.看看每对对称点的坐标有怎样的规律.再和同学讨论一下.已知点A(2,-3)B(-1,2)C(-6,-5)D(0.5,1)E(4,0)关于x轴对称的点A’(
)B’(
)C’(
)D’(
)E’(
)关于y轴对称的点A’’(
)B’’(
)C’’(
)D’’(
)E’’(
)【总结规律】点(x,y)关于x轴对称的点的坐标为(x,-y),即横坐标相等,纵坐标互为相反数;点(x,y)关于y轴对称的点的坐标为(-x,y),即横坐标互为相反数,纵坐标相等.利用刚才发现的点关于x轴、y轴对称的点的坐标规律,我们可以很容易地在平面直角坐标系中作出与一个图形关于x轴、y轴对称的图形.【例1】①点P(-5,
6)与点Q关于x轴对称,则点Q的坐标为__________.②点M
(a,
-5)与点N(-2,
b)关于x轴对称,则a=_____,
b
=_____.③点P(-5,
6)与点Q关于y轴对称,则点Q的坐标为__________.④点M
(a,
-5)与点N(-2,
b)关于y轴对称,则a=_____,
b
=_____.⑤已知点P(2a+b,-3a)与点P’(8,b+2).若点p与点p’关于x轴对称,则a=_____
b=_______.若点p与点p’关于y轴对称,则a=_____
b=_______.【例2】如图,利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于x轴和y轴对称的图形。
( http: / / www.21cnjy.com )【例3】如下图,四边形ABCD的四个顶点
( http: / / www.21cnjy.com )的坐标分别为A(-5,1),B(-2,1),C(-2,5),D(-5,4),分别作出四边形ABCD关于y轴和x轴对称的图形。
( http: / / www.21cnjy.com )【练习】课本Р45
练习21.点关于某条直线对称的点的坐标可以通过寻找线段之间的关系来求.2、(x,y)关于x轴对称的点的坐标为(x
( http: / / www.21cnjy.com ),-y),即横坐标相等,纵坐标互为相反数;点(x,y)关于y轴对称的点的坐标为(-x,y),即横坐标互为相反数,纵坐标相等.3、如果作关于直线x=3(记为m)和直线y=-4(记为n)对称的图形,你能发现对应点的坐标之间的关系吗
学生动手画图,观察各个对称点与原来的点之间坐标的关系,经过讨论得出规律.教师引导,学生自主探索发现关于x轴、y轴对称的每组对称点坐标的规律.直接应用关于x、y轴对称点的坐标特征得出结果。学生根据关于x、y轴对称点的坐标特征,首先求出各点关于x轴、y轴的对称点,然后再连接对称点即可.本活动主要巩固加深学生对利用坐标表示轴对称的理解,所以要特别关注学生对对称点的坐标的求解过程.
板书设计
( http: / / www.21cnjy.com )
作业布置
P71
预习内容
第7课时
等腰三角形(1)
课后反思
利用坐标特征进行数学应用,是初一已经学过的
( http: / / www.21cnjy.com ),这里方程思想和数形结合思想必须继续训练,放手由学生进行自我训练、自我评价,感觉在学生评价上力度还需更加大些。
