苏科版八年级下《第9章中心对称图形——平行四边形》单元测试含答案解析
文档属性
| 名称 | 苏科版八年级下《第9章中心对称图形——平行四边形》单元测试含答案解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 90.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-14 00:00:00 | ||
图片预览



文档简介
《第9章
中心对称图形》
一、选择题
1.已知下列命题中:(1)矩形是轴对称图形,且有两条对称轴;(2)两条对角线相等的四边形是矩形;(3)有两个角相等的平行四边形是矩形;(4)两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
2.平行四边形内角平分线能够围成的四边形是( )
A.梯形
B.矩形
C.正方形
D.不是平行四边形
3.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
A.10cm
B.7cm
C.5cm
D.4cm
4.菱形具有而矩形不一定具有的性质是( )
A.对边平行
B.对角相等
C.对角线互相平分
D.对角线互相垂直
二、填空题
5.如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF= °.
6.已知菱形的周长为52,一条对角线长是24,则另一条对角线长是 .
7.菱形的两邻角的度数之比为l:3,边长为5,则高为 .
8.如果四边形ABCD满足 条件,那么这个四边形的对角线AC和BD互相垂直(只需填写一组你认为适当的条件).
三、解答题
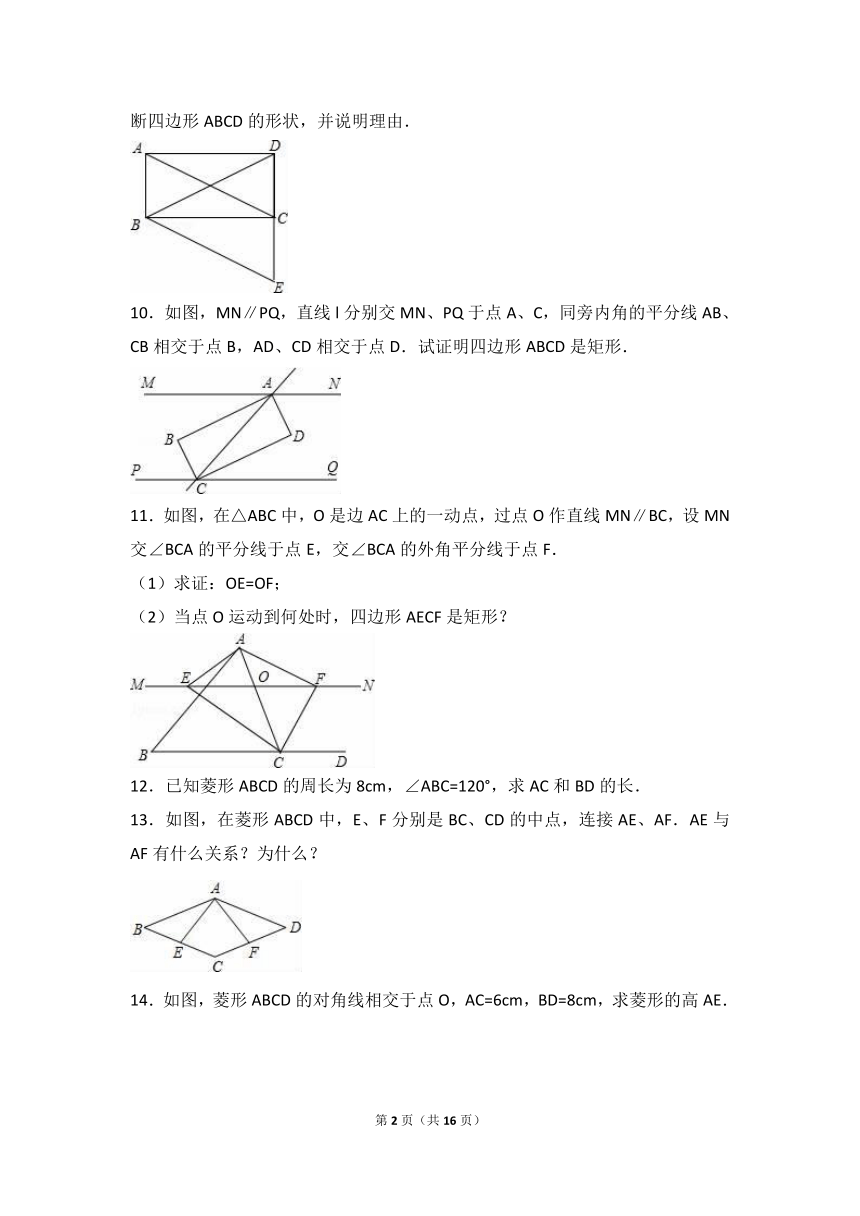
9.如图,BC是等腰三角形BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
10.如图,MN∥PQ,直线l分别交MN、PQ于点A、C,同旁内角的平分线AB、CB相交于点B,AD、CD相交于点D.试证明四边形ABCD是矩形.
11.如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形?
12.已知菱形ABCD的周长为8cm,∠ABC=120°,求AC和BD的长.
13.如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.AE与AF有什么关系?为什么?
14.如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
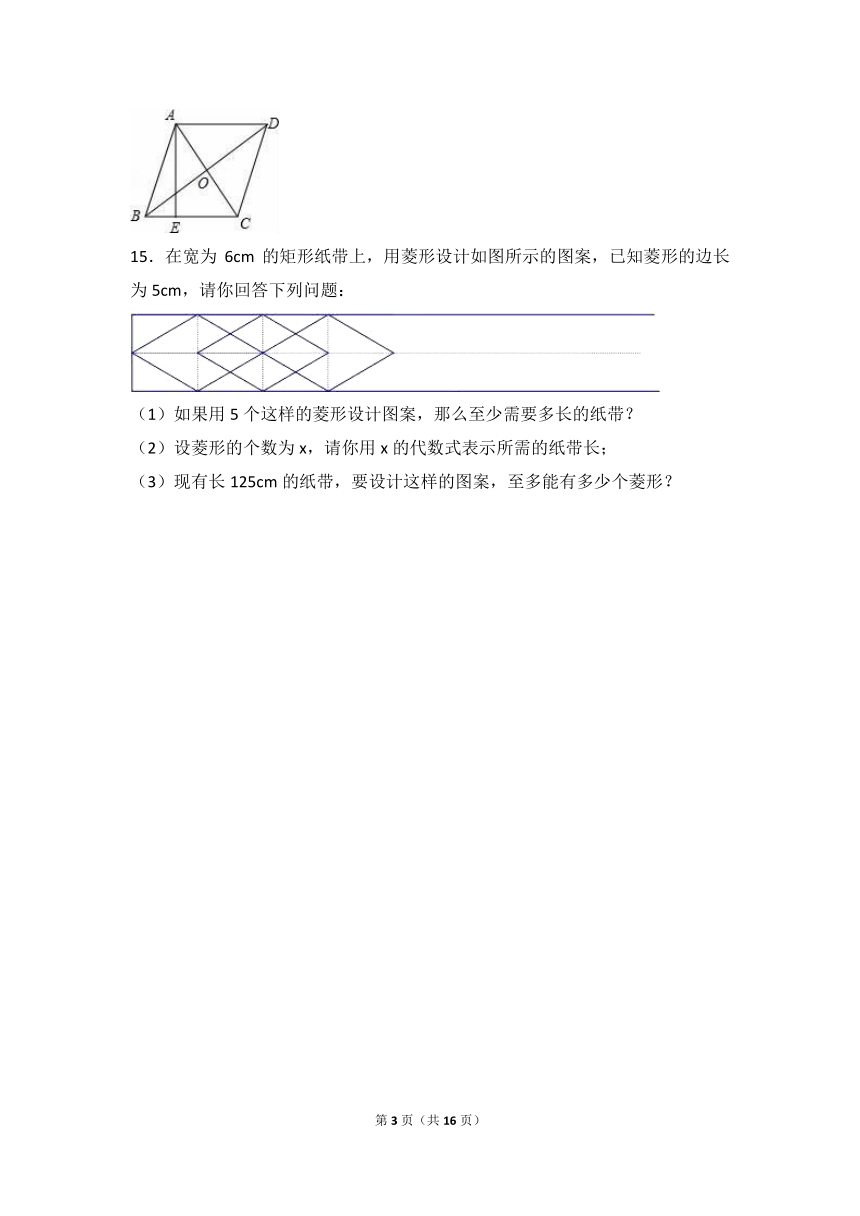
15.在宽为6cm的矩形纸带上,用菱形设计如图所示的图案,已知菱形的边长为5cm,请你回答下列问题:
(1)如果用5个这样的菱形设计图案,那么至少需要多长的纸带?
(2)设菱形的个数为x,请你用x的代数式表示所需的纸带长;
(3)现有长125cm的纸带,要设计这样的图案,至多能有多少个菱形?
《第9章
中心对称图形》
参考答案与试题解析
一、选择题
1.已知下列命题中:(1)矩形是轴对称图形,且有两条对称轴;(2)两条对角线相等的四边形是矩形;(3)有两个角相等的平行四边形是矩形;(4)两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
【考点】矩形的判定与性质.
【分析】根据矩形的轴对称性、矩形的判定和矩形的性质逐项分析即可得到正确命题的个数.
【解答】解:已知如图:
(1)矩形是轴对称图形,对边中点连线所在的直线是它的对称轴,并且有两条,故该选项正确;
(2)只有两条对角线相等的平行四边形是矩形;故该选项错误;
(3)所有的平行四边形对角都相等,但不一定是矩形,故该选项错误;
(4)两条对角线互相平分的四边形是平行四边形,再加对角线相等则为矩形,故该选项正确;
所以其中正确的有(1)和(4).
故选C.
【点评】本题考查了矩形的轴对称性以及矩形的性质和矩形的判定,准确掌握其性质和判定是解题的关键.
2.平行四边形内角平分线能够围成的四边形是( )
A.梯形
B.矩形
C.正方形
D.不是平行四边形
【考点】矩形的判定;平行四边形的性质.
【分析】作出图形,根据平行四边形的邻角互补以及角平分线的定义求出∠AEB=90°,同理可求∠F、∠FGH、∠H都是90°,再根据四个角都是直角的四边形是矩形解答.
【解答】解:∵四边形ABCD是平行四边形,
∴∠BAD+∠ABC=180°,
∵AE、BE分别是∠BAD、∠ABC的平分线,
∴∠BAE+∠ABE=∠BAD+∠ABC=×180°=90°,
∴∠AEB=90°,
∴∠FEH=90°,
同理可求∠F=90°,∠FGH=90°,∠H=90°,
∴四边形EFGH是矩形.
故选B.
【点评】本题考查了矩形的判定,平行四边形的邻角互补,角平分线的定义,注意整体思想的利用.
3.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
A.10cm
B.7cm
C.5cm
D.4cm
【考点】菱形的性质.
【分析】根据菱形的性质,可得到直角三角形,再利用勾股定理可求出边长.
【解答】解:∵菱形的对角线互相垂直平分,
∴两条对角线的一半与菱形的边长构成直角三角形,
∴菱形的边长==5cm,
故选C.
【点评】本题主要利用了菱形的对角线互相垂直平分的性质,以及勾股定理的内容.
4.菱形具有而矩形不一定具有的性质是( )
A.对边平行
B.对角相等
C.对角线互相平分
D.对角线互相垂直
【考点】矩形的性质;菱形的性质.
【分析】菱形与矩形都是平行四边形,故平行四边形的性质二者都具有,因此A,B,C都不能选,对角线中二者不同的是:菱形的对角线互相垂直且平分每一组对角,而矩形的对角线则相等,故选D答案.
【解答】解;∵菱形与矩形都是平行四边形,A,B,C是平行四边形的性质,
∴二者都具有,故此三个选项都不正确,
由于菱形的对角线互相垂直且平分每一组对角,而矩形的对角线则相等,
故选:D.
【点评】此题主要考查了菱形及矩形的性质,关键是需要同学们熟记二者的性质.
二、填空题
5.如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF= 75 °.
【考点】矩形的性质.
【专题】推理填空题.
【分析】根据DF平分∠ADC与∠BDF=15°可以计算出∠CDO=60°,再根据矩形的对角线相等且互相平分可得OD=OC,从而得到△OCD是等边三角形,再证明△COF是等腰三角形,然后根据三角形内角和定理解答即可.
【解答】解:∵DF平分∠ADC,
∴∠CDF=45°,
∴△CDF是等腰直角三角形,
∴CD=CF,
∵∠BDF=15°,
∴∠CDO=∠CDF+∠BDF=45°+15°=60°,
在矩形ABCD中,OD=OC,
∴△OCD是等边三角形,
∴OC=CD,∠OCD=60°,
∴OC=CF,∠OCF=90°﹣∠OCD=90°﹣60°=30°,
在△COF中,∠COF=(180°﹣30°)=75°.
故答案为:75.
【点评】本题考查了矩形的性质,等边三角形的判定与性质,等腰三角形的性质,角平分线的定义,熟记各性质并判断出△OCD是等边三角形是解决本题的关键.
6.已知菱形的周长为52,一条对角线长是24,则另一条对角线长是 10 .
【考点】菱形的性质;勾股定理.
【分析】首先根据题意画出图形,即可得菱形的边长,又由菱形的性质,利用勾股定理,可求得OB的长,继而求得答案.
【解答】解:根据题意得:菱形ABCD的周长为52,一条对角线长AC=6,
∴菱形的边长AB=13,AC⊥BD,OA=AC=12,
∴OB==5,
∴BD=2OB=10,
即另一条对角线的长为10.
故答案为:10.
【点评】此题考查了菱形的性质以及勾股定理.此题比较简单,注意掌握数形结合思想的应用.
7.菱形的两邻角的度数之比为l:3,边长为5,则高为 5 .
【考点】菱形的性质;平行线的性质;勾股定理;等腰直角三角形.
【专题】计算题.
【分析】菱形ABCD的边长BC=5,CE为高,∠B:∠A=1:3,根据菱形的性质得AD∥BC,则∠A+∠B=180°,可计算出∠B=45°,而CE为高,得到△BCE为等腰直角三角形,根据等腰直角三角形的性质得CE=BC,把BC=5代入计算即可.
【解答】解:如图,菱形ABCD的边长BC=5,CE为高,∠B:∠A=1:3,
∵AD∥BC,
∴∠A+∠B=180°,
∴∠B+3∠B=180°,
∴∠B=45°,
而CE为高,
∴△BCE为等腰直角三角形,
∴BC=CE,
∴CE=BC=×5=5.
故答案为:5.
【点评】本题考查了菱形的性质:菱形的对边分别平行,四条边都相等,两条对角线互相垂直平分,并且分别平分两组内角.也考查了等腰直角三角形的判定与性质.
8.如果四边形ABCD满足 四边形ABCD是菱形或正方形 条件,那么这个四边形的对角线AC和BD互相垂直(只需填写一组你认为适当的条件).
【考点】正方形的性质;菱形的性质.
【专题】开放型.
【分析】符合对角线互相垂直的四边形有:菱形、正方形,选择一个即可.
【解答】解:根据四边形的性质可得到对角线互相垂直的有菱形和正方形,从而答案为:四边形ABCD是菱形或正方形.
【点评】此题主要考查菱形和正方形的对角线的性质.
三、解答题
9.(2016春 天河区校级期中)如图,BC是等腰三角形BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
【考点】矩形的判定;等腰三角形的性质;平行四边形的性质.
【分析】根据平行四边形的性质可以证得AB与CD平行且相等,则四边形ABCD是平行四边形,再证得对角线相等即可证得.
【解答】解:四边形ABCD是矩形,
理由:∵BC是等腰△BED底边ED上的高,
∴EC=CD,
∵四边形ABEC是平行四边形,
∴AB∥CD,AB=CE=CD,AC=BE,
∴四边形ABCD是平行四边形.
∵AC=BE,BE=BD,
∴AC=BD,
∴四边形ABCD是矩形.
【点评】本题主要考查了平行四边形的性质以及矩形的判定,关键是掌握对角线相等的平行四边形是矩形.
10.如图,MN∥PQ,直线l分别交MN、PQ于点A、C,同旁内角的平分线AB、CB相交于点B,AD、CD相交于点D.试证明四边形ABCD是矩形.
【考点】矩形的判定.
【专题】证明题.
【分析】首先推出∠BAC=∠DCA,继而推出AB∥CD;推出∠BCA=∠DAC,进而推出AD∥CB,因此四边形ABCD平行四边形,再证明∠ABC=90°,可得平行四边形ABCD是矩形.
【解答】证明:∵MN∥PQ,
∴∠MAC=∠ACQ、∠ACP=∠NAC,
∵AB、CD分别平分∠MAC和∠ACQ,
∴∠BAC=∠MAC、∠DCA=∠ACQ,
又∵∠MAC=∠ACQ,
∴∠BAC=∠DCA,
∴AB∥CD,
∵AD、CB分别平分∠ACP和∠NAC,
∴∠BCA=∠ACP、∠DAC=∠NAC,
又∵∠ACP=∠NAC,
∴∠BCA=∠DAC,
∴AD∥CB,
又∵AB∥CD,
∴四边形ABCD平行四边形,
∵∠BAC=∠MAC,∠ACB=∠ACP,
又∵∠MAC+∠ACP=180°,
∴∠BAC+∠ACB=90°,
∴∠ABC=90°,
∴平行四边形ABCD是矩形.
【点评】此题主要考查了矩形的判定,关键是掌握有一个角是直角的平行四边形是矩形.
11.(2016春 柘城县期中)如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形?
【考点】矩形的判定.
【分析】(1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD及等角对等边即可证得OE=OF;
(2)根据矩形的性质可知:对角线且互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.
【解答】(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)解:当O运动到AC中点时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.
【点评】此题主要考查了矩形的判定,关键是掌握有一个角为直角的平行四边形是矩形.
12.已知菱形ABCD的周长为8cm,∠ABC=120°,求AC和BD的长.
【考点】菱形的性质.
【分析】根据菱形的四条边都相等求出边长AB,再根据菱形的对角线平分一组对角线求出∠ABO=60°,再根据直角三角形30°角所对的直角边等于斜边的一半求出OB,然后利用勾股定理列式求出OA,最后根据菱形的对角线互相平分求解即可.
【解答】解:∵菱形ABCD的周长为8cm,
∴AB=8÷4=2cm,
∵∠ABC=120°,
∴∠ABO=60°,
∵菱形的对角线AC⊥BD,
∴∠BAO=90°﹣60°=30°,
∴OB=AB=×2=1cm,
由勾股定理得,OA===cm,
∴AC=2OA=2cm,BD=2OB=2cm.
【点评】本题考查了菱形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质是解题的关键,作出图形更形象直观.
13.如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.AE与AF有什么关系?为什么?
【考点】菱形的性质.
【分析】根据菱形的性质可以得出AB=BC=CD=AD,∠B=∠D,进而就可以得出△ABE≌△ADF,从而得出AE=AF.
【解答】解:AE=AF
理由:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D,
∴BC=.
∵E、F分别是BC、CD的中点,
∴BE=BC,DF=CD,
∴BE=DF.
在△ABE和△ADF中
∴△ABE≌△ADF(SAS),
∴AE=AF.
【点评】本题考查了菱形的性质的运用,线段的中点的性质的运用,全等三角形的判定及性质的运用,解答时运用菱形的性质证明三角形全等是关键.
14.如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
【考点】菱形的性质.
【分析】根据菱形的对角线互相垂直平分求出OB、OC的长度,再根据勾股定理求出菱形的边BC的长,然后利用菱形的面积等于对角线乘积的一半和底乘以高两种方法列式求解即可.
【解答】解:在菱形ABCD中,
∵AC=6m,BD=8cm,
∴OC=AC=×6=3cm,OB=BD=×8=4cm,
∵AC⊥BD(菱形的对角线互相垂直),
∴BC=5cm,
∴CD=BC=5cm,
S菱形ABCD=CD AE=AC BD,
即5AE=×6×8,
解得AE=4.8cm.
【点评】本题考查了菱形的性质,主要涉及到菱形的对角线互相垂直平分,菱形的对角线平分一组对角,以及菱形的面积的求解,熟练掌握并灵活运用菱形的性质是解题的关键.
15.在宽为6cm的矩形纸带上,用菱形设计如图所示的图案,已知菱形的边长为5cm,请你回答下列问题:
(1)如果用5个这样的菱形设计图案,那么至少需要多长的纸带?
(2)设菱形的个数为x,请你用x的代数式表示所需的纸带长;
(3)现有长125cm的纸带,要设计这样的图案,至多能有多少个菱形?
【考点】菱形的性质.
【分析】(1)如图,根据菱形的性质和勾股定理可以求出BO的值,进而可以得出BD的值,依此类推可以得出两个菱形时纸袋的长度,三个菱形时纸带的长度…进而得出5个菱形时的纸带长度;
(2)根据1个菱形的长度为4×2=8cm,2个菱形的长度为4×3=12cm.3个菱形的长度为4×4=16cm,就可以得出x个菱形的长度为4(x+1)cm;
(3)将4(x+1)≤125建立不等式求出其解,就可以得出结论.
【解答】解:(1)如图,∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5cm,AO=CO=AC=3cm.BO=DO=BD,∠AOB=90°,
∴在Rt△ABO中,由勾股定理,得
BO==4cm,
∴BD=8cm,
由图形得,2个菱形时的长度为:8+4=12cm,
3个菱形时的长度为:12+4=16cm,
4个菱形时的长度为:16+4=20cm,
5个菱形时的长度为:20+4=24cm,
∴5个这样的菱形设计图案,那么至少需要24cm长的纸带;
(2)由图象,得
1个菱形的长度为8=4×2=4(1+1)cm,
2个菱形的长度为12=4×3=4(2+1)cm,
3个菱形的长度为16=4×4=4(3+1)cm,
…
x个菱形的长度为:4(x+1)cm,
(3)由题意,得
4(x+1)≤125,
x≤30,
∵x为整数,
∴x=30.
答:长125cm的纸带,要设计这样的图案,至多能有30个菱形.
【点评】本题考查了菱形的性质的运用,勾股定理的运用,探索规律题的解题方法的运用,一元一次不等式的解法的运用,解答时运用菱形的性质求解是关键.
第17页(共17页)
中心对称图形》
一、选择题
1.已知下列命题中:(1)矩形是轴对称图形,且有两条对称轴;(2)两条对角线相等的四边形是矩形;(3)有两个角相等的平行四边形是矩形;(4)两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
2.平行四边形内角平分线能够围成的四边形是( )
A.梯形
B.矩形
C.正方形
D.不是平行四边形
3.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
A.10cm
B.7cm
C.5cm
D.4cm
4.菱形具有而矩形不一定具有的性质是( )
A.对边平行
B.对角相等
C.对角线互相平分
D.对角线互相垂直
二、填空题
5.如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF= °.
6.已知菱形的周长为52,一条对角线长是24,则另一条对角线长是 .
7.菱形的两邻角的度数之比为l:3,边长为5,则高为 .
8.如果四边形ABCD满足 条件,那么这个四边形的对角线AC和BD互相垂直(只需填写一组你认为适当的条件).
三、解答题
9.如图,BC是等腰三角形BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
10.如图,MN∥PQ,直线l分别交MN、PQ于点A、C,同旁内角的平分线AB、CB相交于点B,AD、CD相交于点D.试证明四边形ABCD是矩形.
11.如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形?
12.已知菱形ABCD的周长为8cm,∠ABC=120°,求AC和BD的长.
13.如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.AE与AF有什么关系?为什么?
14.如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
15.在宽为6cm的矩形纸带上,用菱形设计如图所示的图案,已知菱形的边长为5cm,请你回答下列问题:
(1)如果用5个这样的菱形设计图案,那么至少需要多长的纸带?
(2)设菱形的个数为x,请你用x的代数式表示所需的纸带长;
(3)现有长125cm的纸带,要设计这样的图案,至多能有多少个菱形?
《第9章
中心对称图形》
参考答案与试题解析
一、选择题
1.已知下列命题中:(1)矩形是轴对称图形,且有两条对称轴;(2)两条对角线相等的四边形是矩形;(3)有两个角相等的平行四边形是矩形;(4)两条对角线相等且互相平分的四边形是矩形.其中正确的有( )
A.4个
B.3个
C.2个
D.1个
【考点】矩形的判定与性质.
【分析】根据矩形的轴对称性、矩形的判定和矩形的性质逐项分析即可得到正确命题的个数.
【解答】解:已知如图:
(1)矩形是轴对称图形,对边中点连线所在的直线是它的对称轴,并且有两条,故该选项正确;
(2)只有两条对角线相等的平行四边形是矩形;故该选项错误;
(3)所有的平行四边形对角都相等,但不一定是矩形,故该选项错误;
(4)两条对角线互相平分的四边形是平行四边形,再加对角线相等则为矩形,故该选项正确;
所以其中正确的有(1)和(4).
故选C.
【点评】本题考查了矩形的轴对称性以及矩形的性质和矩形的判定,准确掌握其性质和判定是解题的关键.
2.平行四边形内角平分线能够围成的四边形是( )
A.梯形
B.矩形
C.正方形
D.不是平行四边形
【考点】矩形的判定;平行四边形的性质.
【分析】作出图形,根据平行四边形的邻角互补以及角平分线的定义求出∠AEB=90°,同理可求∠F、∠FGH、∠H都是90°,再根据四个角都是直角的四边形是矩形解答.
【解答】解:∵四边形ABCD是平行四边形,
∴∠BAD+∠ABC=180°,
∵AE、BE分别是∠BAD、∠ABC的平分线,
∴∠BAE+∠ABE=∠BAD+∠ABC=×180°=90°,
∴∠AEB=90°,
∴∠FEH=90°,
同理可求∠F=90°,∠FGH=90°,∠H=90°,
∴四边形EFGH是矩形.
故选B.
【点评】本题考查了矩形的判定,平行四边形的邻角互补,角平分线的定义,注意整体思想的利用.
3.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )
A.10cm
B.7cm
C.5cm
D.4cm
【考点】菱形的性质.
【分析】根据菱形的性质,可得到直角三角形,再利用勾股定理可求出边长.
【解答】解:∵菱形的对角线互相垂直平分,
∴两条对角线的一半与菱形的边长构成直角三角形,
∴菱形的边长==5cm,
故选C.
【点评】本题主要利用了菱形的对角线互相垂直平分的性质,以及勾股定理的内容.
4.菱形具有而矩形不一定具有的性质是( )
A.对边平行
B.对角相等
C.对角线互相平分
D.对角线互相垂直
【考点】矩形的性质;菱形的性质.
【分析】菱形与矩形都是平行四边形,故平行四边形的性质二者都具有,因此A,B,C都不能选,对角线中二者不同的是:菱形的对角线互相垂直且平分每一组对角,而矩形的对角线则相等,故选D答案.
【解答】解;∵菱形与矩形都是平行四边形,A,B,C是平行四边形的性质,
∴二者都具有,故此三个选项都不正确,
由于菱形的对角线互相垂直且平分每一组对角,而矩形的对角线则相等,
故选:D.
【点评】此题主要考查了菱形及矩形的性质,关键是需要同学们熟记二者的性质.
二、填空题
5.如图,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于点E,交BC于点F,∠BDF=15°,则∠COF= 75 °.
【考点】矩形的性质.
【专题】推理填空题.
【分析】根据DF平分∠ADC与∠BDF=15°可以计算出∠CDO=60°,再根据矩形的对角线相等且互相平分可得OD=OC,从而得到△OCD是等边三角形,再证明△COF是等腰三角形,然后根据三角形内角和定理解答即可.
【解答】解:∵DF平分∠ADC,
∴∠CDF=45°,
∴△CDF是等腰直角三角形,
∴CD=CF,
∵∠BDF=15°,
∴∠CDO=∠CDF+∠BDF=45°+15°=60°,
在矩形ABCD中,OD=OC,
∴△OCD是等边三角形,
∴OC=CD,∠OCD=60°,
∴OC=CF,∠OCF=90°﹣∠OCD=90°﹣60°=30°,
在△COF中,∠COF=(180°﹣30°)=75°.
故答案为:75.
【点评】本题考查了矩形的性质,等边三角形的判定与性质,等腰三角形的性质,角平分线的定义,熟记各性质并判断出△OCD是等边三角形是解决本题的关键.
6.已知菱形的周长为52,一条对角线长是24,则另一条对角线长是 10 .
【考点】菱形的性质;勾股定理.
【分析】首先根据题意画出图形,即可得菱形的边长,又由菱形的性质,利用勾股定理,可求得OB的长,继而求得答案.
【解答】解:根据题意得:菱形ABCD的周长为52,一条对角线长AC=6,
∴菱形的边长AB=13,AC⊥BD,OA=AC=12,
∴OB==5,
∴BD=2OB=10,
即另一条对角线的长为10.
故答案为:10.
【点评】此题考查了菱形的性质以及勾股定理.此题比较简单,注意掌握数形结合思想的应用.
7.菱形的两邻角的度数之比为l:3,边长为5,则高为 5 .
【考点】菱形的性质;平行线的性质;勾股定理;等腰直角三角形.
【专题】计算题.
【分析】菱形ABCD的边长BC=5,CE为高,∠B:∠A=1:3,根据菱形的性质得AD∥BC,则∠A+∠B=180°,可计算出∠B=45°,而CE为高,得到△BCE为等腰直角三角形,根据等腰直角三角形的性质得CE=BC,把BC=5代入计算即可.
【解答】解:如图,菱形ABCD的边长BC=5,CE为高,∠B:∠A=1:3,
∵AD∥BC,
∴∠A+∠B=180°,
∴∠B+3∠B=180°,
∴∠B=45°,
而CE为高,
∴△BCE为等腰直角三角形,
∴BC=CE,
∴CE=BC=×5=5.
故答案为:5.
【点评】本题考查了菱形的性质:菱形的对边分别平行,四条边都相等,两条对角线互相垂直平分,并且分别平分两组内角.也考查了等腰直角三角形的判定与性质.
8.如果四边形ABCD满足 四边形ABCD是菱形或正方形 条件,那么这个四边形的对角线AC和BD互相垂直(只需填写一组你认为适当的条件).
【考点】正方形的性质;菱形的性质.
【专题】开放型.
【分析】符合对角线互相垂直的四边形有:菱形、正方形,选择一个即可.
【解答】解:根据四边形的性质可得到对角线互相垂直的有菱形和正方形,从而答案为:四边形ABCD是菱形或正方形.
【点评】此题主要考查菱形和正方形的对角线的性质.
三、解答题
9.(2016春 天河区校级期中)如图,BC是等腰三角形BED底边DE上的高,四边形ABEC是平行四边形.判断四边形ABCD的形状,并说明理由.
【考点】矩形的判定;等腰三角形的性质;平行四边形的性质.
【分析】根据平行四边形的性质可以证得AB与CD平行且相等,则四边形ABCD是平行四边形,再证得对角线相等即可证得.
【解答】解:四边形ABCD是矩形,
理由:∵BC是等腰△BED底边ED上的高,
∴EC=CD,
∵四边形ABEC是平行四边形,
∴AB∥CD,AB=CE=CD,AC=BE,
∴四边形ABCD是平行四边形.
∵AC=BE,BE=BD,
∴AC=BD,
∴四边形ABCD是矩形.
【点评】本题主要考查了平行四边形的性质以及矩形的判定,关键是掌握对角线相等的平行四边形是矩形.
10.如图,MN∥PQ,直线l分别交MN、PQ于点A、C,同旁内角的平分线AB、CB相交于点B,AD、CD相交于点D.试证明四边形ABCD是矩形.
【考点】矩形的判定.
【专题】证明题.
【分析】首先推出∠BAC=∠DCA,继而推出AB∥CD;推出∠BCA=∠DAC,进而推出AD∥CB,因此四边形ABCD平行四边形,再证明∠ABC=90°,可得平行四边形ABCD是矩形.
【解答】证明:∵MN∥PQ,
∴∠MAC=∠ACQ、∠ACP=∠NAC,
∵AB、CD分别平分∠MAC和∠ACQ,
∴∠BAC=∠MAC、∠DCA=∠ACQ,
又∵∠MAC=∠ACQ,
∴∠BAC=∠DCA,
∴AB∥CD,
∵AD、CB分别平分∠ACP和∠NAC,
∴∠BCA=∠ACP、∠DAC=∠NAC,
又∵∠ACP=∠NAC,
∴∠BCA=∠DAC,
∴AD∥CB,
又∵AB∥CD,
∴四边形ABCD平行四边形,
∵∠BAC=∠MAC,∠ACB=∠ACP,
又∵∠MAC+∠ACP=180°,
∴∠BAC+∠ACB=90°,
∴∠ABC=90°,
∴平行四边形ABCD是矩形.
【点评】此题主要考查了矩形的判定,关键是掌握有一个角是直角的平行四边形是矩形.
11.(2016春 柘城县期中)如图,在△ABC中,O是边AC上的一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形?
【考点】矩形的判定.
【分析】(1)根据MN∥BC,CE平分∠ACB,CF平分∠ACD及等角对等边即可证得OE=OF;
(2)根据矩形的性质可知:对角线且互相平分,即AO=CO,OE=OF,故当点O运动到AC的中点时,四边形AECF是矩形.
【解答】(1)证明:∵MN∥BC,CE平分∠ACB,CF平分∠ACD,
∴∠BCE=∠ACE=∠OEC,∠OCF=∠FCD=∠OFC,
∴OE=OC,OC=OF,
∴OE=OF.
(2)解:当O运动到AC中点时,四边形AECF是矩形,
∵AO=CO,OE=OF,
∴四边形AECF是平行四边形,
∵∠ECA+∠ACF=∠BCD,
∴∠ECF=90°,
∴四边形AECF是矩形.
【点评】此题主要考查了矩形的判定,关键是掌握有一个角为直角的平行四边形是矩形.
12.已知菱形ABCD的周长为8cm,∠ABC=120°,求AC和BD的长.
【考点】菱形的性质.
【分析】根据菱形的四条边都相等求出边长AB,再根据菱形的对角线平分一组对角线求出∠ABO=60°,再根据直角三角形30°角所对的直角边等于斜边的一半求出OB,然后利用勾股定理列式求出OA,最后根据菱形的对角线互相平分求解即可.
【解答】解:∵菱形ABCD的周长为8cm,
∴AB=8÷4=2cm,
∵∠ABC=120°,
∴∠ABO=60°,
∵菱形的对角线AC⊥BD,
∴∠BAO=90°﹣60°=30°,
∴OB=AB=×2=1cm,
由勾股定理得,OA===cm,
∴AC=2OA=2cm,BD=2OB=2cm.
【点评】本题考查了菱形的性质,直角三角形30°角所对的直角边等于斜边的一半的性质,熟记各性质是解题的关键,作出图形更形象直观.
13.如图,在菱形ABCD中,E、F分别是BC、CD的中点,连接AE、AF.AE与AF有什么关系?为什么?
【考点】菱形的性质.
【分析】根据菱形的性质可以得出AB=BC=CD=AD,∠B=∠D,进而就可以得出△ABE≌△ADF,从而得出AE=AF.
【解答】解:AE=AF
理由:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,∠B=∠D,
∴BC=.
∵E、F分别是BC、CD的中点,
∴BE=BC,DF=CD,
∴BE=DF.
在△ABE和△ADF中
∴△ABE≌△ADF(SAS),
∴AE=AF.
【点评】本题考查了菱形的性质的运用,线段的中点的性质的运用,全等三角形的判定及性质的运用,解答时运用菱形的性质证明三角形全等是关键.
14.如图,菱形ABCD的对角线相交于点O,AC=6cm,BD=8cm,求菱形的高AE.
【考点】菱形的性质.
【分析】根据菱形的对角线互相垂直平分求出OB、OC的长度,再根据勾股定理求出菱形的边BC的长,然后利用菱形的面积等于对角线乘积的一半和底乘以高两种方法列式求解即可.
【解答】解:在菱形ABCD中,
∵AC=6m,BD=8cm,
∴OC=AC=×6=3cm,OB=BD=×8=4cm,
∵AC⊥BD(菱形的对角线互相垂直),
∴BC=5cm,
∴CD=BC=5cm,
S菱形ABCD=CD AE=AC BD,
即5AE=×6×8,
解得AE=4.8cm.
【点评】本题考查了菱形的性质,主要涉及到菱形的对角线互相垂直平分,菱形的对角线平分一组对角,以及菱形的面积的求解,熟练掌握并灵活运用菱形的性质是解题的关键.
15.在宽为6cm的矩形纸带上,用菱形设计如图所示的图案,已知菱形的边长为5cm,请你回答下列问题:
(1)如果用5个这样的菱形设计图案,那么至少需要多长的纸带?
(2)设菱形的个数为x,请你用x的代数式表示所需的纸带长;
(3)现有长125cm的纸带,要设计这样的图案,至多能有多少个菱形?
【考点】菱形的性质.
【分析】(1)如图,根据菱形的性质和勾股定理可以求出BO的值,进而可以得出BD的值,依此类推可以得出两个菱形时纸袋的长度,三个菱形时纸带的长度…进而得出5个菱形时的纸带长度;
(2)根据1个菱形的长度为4×2=8cm,2个菱形的长度为4×3=12cm.3个菱形的长度为4×4=16cm,就可以得出x个菱形的长度为4(x+1)cm;
(3)将4(x+1)≤125建立不等式求出其解,就可以得出结论.
【解答】解:(1)如图,∵四边形ABCD是菱形,
∴AB=BC=CD=AD=5cm,AO=CO=AC=3cm.BO=DO=BD,∠AOB=90°,
∴在Rt△ABO中,由勾股定理,得
BO==4cm,
∴BD=8cm,
由图形得,2个菱形时的长度为:8+4=12cm,
3个菱形时的长度为:12+4=16cm,
4个菱形时的长度为:16+4=20cm,
5个菱形时的长度为:20+4=24cm,
∴5个这样的菱形设计图案,那么至少需要24cm长的纸带;
(2)由图象,得
1个菱形的长度为8=4×2=4(1+1)cm,
2个菱形的长度为12=4×3=4(2+1)cm,
3个菱形的长度为16=4×4=4(3+1)cm,
…
x个菱形的长度为:4(x+1)cm,
(3)由题意,得
4(x+1)≤125,
x≤30,
∵x为整数,
∴x=30.
答:长125cm的纸带,要设计这样的图案,至多能有30个菱形.
【点评】本题考查了菱形的性质的运用,勾股定理的运用,探索规律题的解题方法的运用,一元一次不等式的解法的运用,解答时运用菱形的性质求解是关键.
第17页(共17页)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
