19.2 平行四边形的判定 课件
图片预览



文档简介
课件17张PPT。19.2 平行四边形的判定知识回顾1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.2.平四边形的性质:性质3 :平行四边形的对角线互相平分.性质2 :平行四边形的对角相等.性质1 :平行四边形的对边相等. 平行四边形的定义有两层意思:(1) 若一个四边形
是平行四边形,则它的两组对边就分别平行;(2)若一
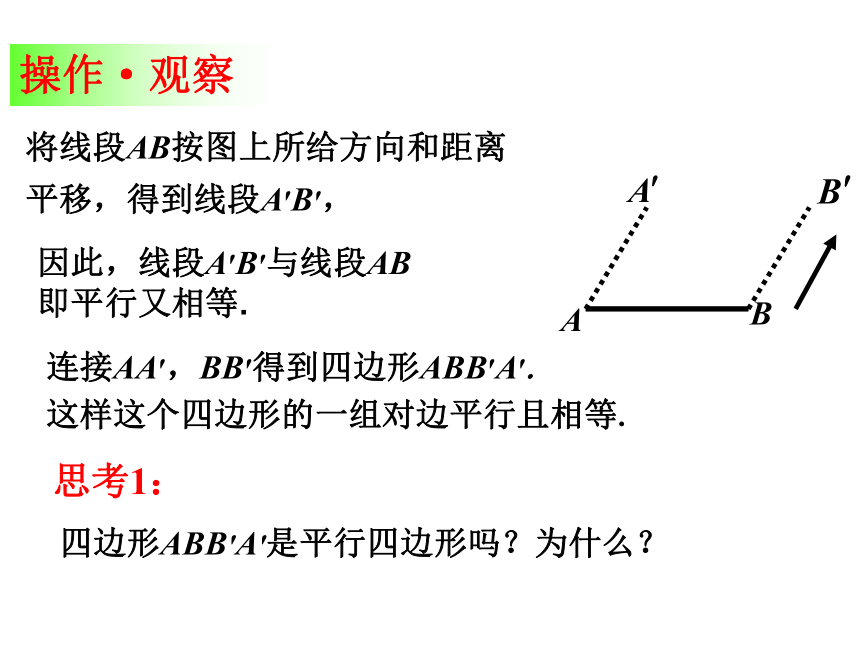
个四边形的两组对边分别平行,则它是平行四边形.操作·观察AB将线段AB按图上所给方向和距离
平移,得到线段A′B′,连接AA′,BB′得到四边形ABB′A′.这样这个四边形的一组对边平行且相等.思考1:四边形ABB′A′是平行四边形吗?为什么?因此,线段A′B′与线段AB
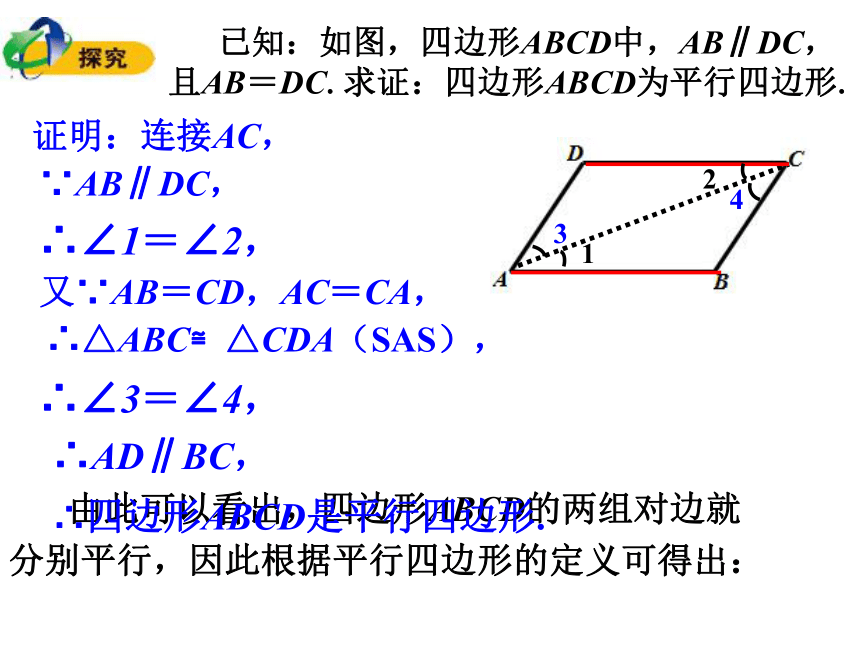
即平行又相等. 已知:如图,四边形ABCD中,AB∥DC,
且AB=DC.求证:四边形ABCD为平行四边形. 证明:连接AC,∵AB∥DC,∴∠1=∠2,又∵AB=CD,AC=CA,∴△ABC≌△CDA(SAS),∴∠3=∠4,∴AD∥BC, 由此可以看出,四边形ABCD的两组对边就
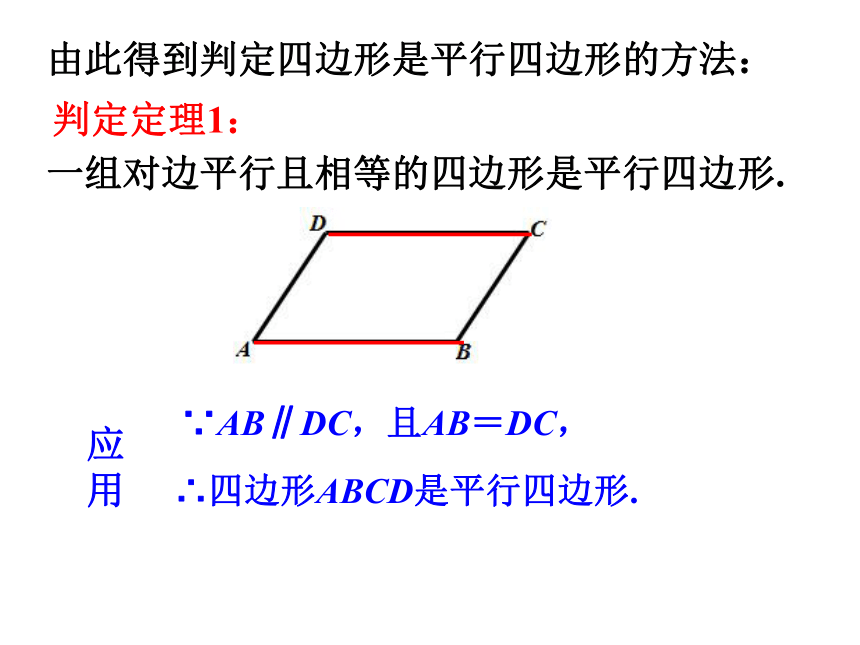
分别平行,因此根据平行四边形的定义可得出:1234∴四边形ABCD是平行四边形.由此得到判定四边形是平行四边形的方法:判定定理1:一组对边平行且相等的四边形是平行四边形.∵AB∥DC,且AB=DC,∴四边形ABCD是平行四边形.应
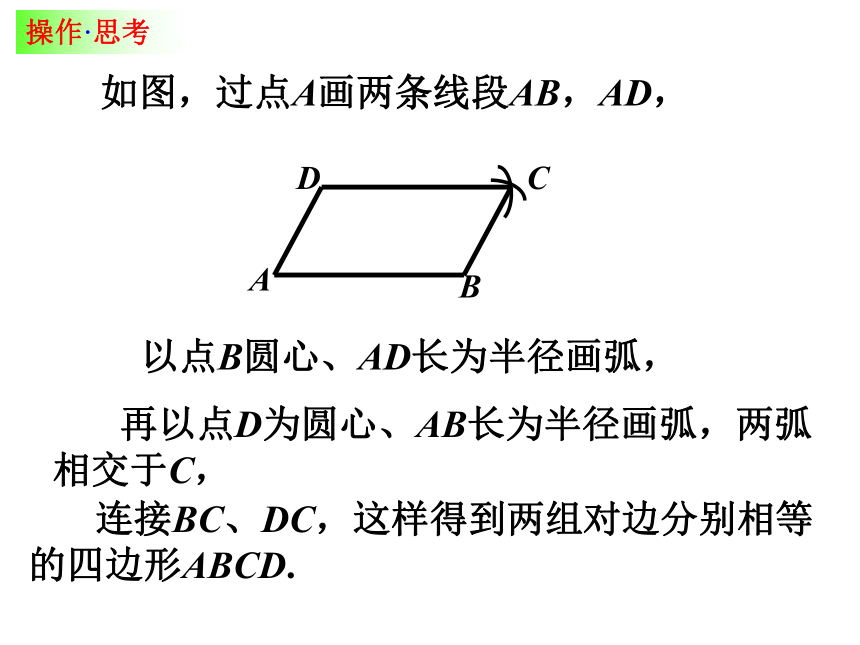
用操作·思考如图,过点A画两条线段AB,AD,以点B圆心、AD长为半径画弧, 再以点D为圆心、AB长为半径画弧,两弧
相交于C, 连接BC、DC,这样得到两组对边分别相等
的四边形ABCD.ABDC思考2: 这样做出来的四边形是平行四边形吗?
为什么?通过画图我们知道:AB=DC,AD=BC,又∵AC=CA,∴△ABC≌△CDA,∴∠CAB=∠DCA,∴AB∥DC, 因此,我们根据第一条判定方法即可得到
此四边形为平行四边形.操作·思考如图,作两条直线l1,l2相交于点O,OABCD在直线l1上截取OA=OC,
在直线l2上截取OB=OD,连接AB,BC,CD,DA, 这样画出来的四边形ABCD的对角线就互相平分.
l1l2这个四边形是平行四边形吗?思考3:由作图可知:OA=OC,OB=OD,又∵∠AOD=∠BOC(对顶角相等),∴△AOD≌△BOC,∴∠DAO=∠BCO,∴AD∥BC,同理可得:AB∥DC,∴四边形ABCD是平行四边形. 由上面操作、探讨可得出判定四边形是
平行四边形的方法还有:判定定理2:两组对边分别相等的四边形是平行四边形.判定定理3:对角线互相平分的四边形是平行四边形.∵AB=DC,BC=AD,∴四边形ABCD是平行四边形.∵OA=OC,OB=OD,∴四边形ABCD是平行四边形.应
用应
用典例讲解 1.已知:如图,点E,F是 ABCD的对角线AC上两
点,且AE=CF,求证:四边形BEDF是平行四边形.证明:连接BD交AC于点O,∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵AE=CF,∴AO-AE=CO-CF,∴四边形BEDF是平行四边形.O即 OE=OF, 2.如图,四边形ABCD是平行四边形,E,F
是对角线BD上的点,∠1=∠2.求证: AF∥CE.证明:∵四边形ABCD
是平行四边形,∴AB=CD,AB∥CD,∴∠3=∠4,∵∠1=∠2,∴∠AEB=∠DFC,∴ △ABE≌△CDF(ASA)∴AE=CF,又∵∠1=∠2,∴AE∥CF,∴四边形AECF是平行四边形,∴AF∥CE.随堂练习1.已知:如图,在四边形ABCD中,∠A=∠C,
∠B=∠D.试判断四边形ABCD是否是平行四
边形,并说明理由.∵∠A=∠C,∠B=∠D 而∠A+∠B+∠C+∠D=360° ∴2∠A+2∠B=360° ∴∠A+∠B=180° ∴AD//BC 同理可证:AB//CD ∴四边形ABCD是平行四边形 .2.画□ABCD,使AB=2cm,BC=3cm,
AC=4cm.ABCD用直尺画2cm的线段AB,用圆规以A为圆心,4cm为半径画弧,再以B为圆心3cm为半径画弧,两弧交点为C,连接AC,BC,过C做CD=2cm,且平行于AB,连接AD,即可得□ABCD. 3.如图,E,F是四边形ABCD的对角线AC上
两点,AF=CE,DF=BE,DF∥BE,
求证:四边形ABCD是平行四边形.证明:∵DF∥BE,∴∠DFE=∠BEF,∴∠AFD=∠CEB,又∵AF=CE,DF=BE,∴△AFD≌△CEB(SAS),∴∠DAC=∠BCA,AD=BC,∴AD∥BC,∴四边形ABCD是平行四边形.小结与反思平行四边形的判定方法:1.本节课你学习了哪些主要内容,与同伴交流.2.通过本节课的学习你有哪些收获和经验?
谈谈你的感悟.判定1 :一组对边平行且相等的四边形是平行四边形.判定2:两组对边分别相等的四边形是平行四边形.判定3:对角线互相平分的四边形是平行四边形.布置作业课本第85页习题:第8~10题.再见!
是平行四边形,则它的两组对边就分别平行;(2)若一
个四边形的两组对边分别平行,则它是平行四边形.操作·观察AB将线段AB按图上所给方向和距离
平移,得到线段A′B′,连接AA′,BB′得到四边形ABB′A′.这样这个四边形的一组对边平行且相等.思考1:四边形ABB′A′是平行四边形吗?为什么?因此,线段A′B′与线段AB
即平行又相等. 已知:如图,四边形ABCD中,AB∥DC,
且AB=DC.求证:四边形ABCD为平行四边形. 证明:连接AC,∵AB∥DC,∴∠1=∠2,又∵AB=CD,AC=CA,∴△ABC≌△CDA(SAS),∴∠3=∠4,∴AD∥BC, 由此可以看出,四边形ABCD的两组对边就
分别平行,因此根据平行四边形的定义可得出:1234∴四边形ABCD是平行四边形.由此得到判定四边形是平行四边形的方法:判定定理1:一组对边平行且相等的四边形是平行四边形.∵AB∥DC,且AB=DC,∴四边形ABCD是平行四边形.应
用操作·思考如图,过点A画两条线段AB,AD,以点B圆心、AD长为半径画弧, 再以点D为圆心、AB长为半径画弧,两弧
相交于C, 连接BC、DC,这样得到两组对边分别相等
的四边形ABCD.ABDC思考2: 这样做出来的四边形是平行四边形吗?
为什么?通过画图我们知道:AB=DC,AD=BC,又∵AC=CA,∴△ABC≌△CDA,∴∠CAB=∠DCA,∴AB∥DC, 因此,我们根据第一条判定方法即可得到
此四边形为平行四边形.操作·思考如图,作两条直线l1,l2相交于点O,OABCD在直线l1上截取OA=OC,
在直线l2上截取OB=OD,连接AB,BC,CD,DA, 这样画出来的四边形ABCD的对角线就互相平分.
l1l2这个四边形是平行四边形吗?思考3:由作图可知:OA=OC,OB=OD,又∵∠AOD=∠BOC(对顶角相等),∴△AOD≌△BOC,∴∠DAO=∠BCO,∴AD∥BC,同理可得:AB∥DC,∴四边形ABCD是平行四边形. 由上面操作、探讨可得出判定四边形是
平行四边形的方法还有:判定定理2:两组对边分别相等的四边形是平行四边形.判定定理3:对角线互相平分的四边形是平行四边形.∵AB=DC,BC=AD,∴四边形ABCD是平行四边形.∵OA=OC,OB=OD,∴四边形ABCD是平行四边形.应
用应
用典例讲解 1.已知:如图,点E,F是 ABCD的对角线AC上两
点,且AE=CF,求证:四边形BEDF是平行四边形.证明:连接BD交AC于点O,∵四边形ABCD是平行四边形,∴AO=CO,BO=DO,∵AE=CF,∴AO-AE=CO-CF,∴四边形BEDF是平行四边形.O即 OE=OF, 2.如图,四边形ABCD是平行四边形,E,F
是对角线BD上的点,∠1=∠2.求证: AF∥CE.证明:∵四边形ABCD
是平行四边形,∴AB=CD,AB∥CD,∴∠3=∠4,∵∠1=∠2,∴∠AEB=∠DFC,∴ △ABE≌△CDF(ASA)∴AE=CF,又∵∠1=∠2,∴AE∥CF,∴四边形AECF是平行四边形,∴AF∥CE.随堂练习1.已知:如图,在四边形ABCD中,∠A=∠C,
∠B=∠D.试判断四边形ABCD是否是平行四
边形,并说明理由.∵∠A=∠C,∠B=∠D 而∠A+∠B+∠C+∠D=360° ∴2∠A+2∠B=360° ∴∠A+∠B=180° ∴AD//BC 同理可证:AB//CD ∴四边形ABCD是平行四边形 .2.画□ABCD,使AB=2cm,BC=3cm,
AC=4cm.ABCD用直尺画2cm的线段AB,用圆规以A为圆心,4cm为半径画弧,再以B为圆心3cm为半径画弧,两弧交点为C,连接AC,BC,过C做CD=2cm,且平行于AB,连接AD,即可得□ABCD. 3.如图,E,F是四边形ABCD的对角线AC上
两点,AF=CE,DF=BE,DF∥BE,
求证:四边形ABCD是平行四边形.证明:∵DF∥BE,∴∠DFE=∠BEF,∴∠AFD=∠CEB,又∵AF=CE,DF=BE,∴△AFD≌△CEB(SAS),∴∠DAC=∠BCA,AD=BC,∴AD∥BC,∴四边形ABCD是平行四边形.小结与反思平行四边形的判定方法:1.本节课你学习了哪些主要内容,与同伴交流.2.通过本节课的学习你有哪些收获和经验?
谈谈你的感悟.判定1 :一组对边平行且相等的四边形是平行四边形.判定2:两组对边分别相等的四边形是平行四边形.判定3:对角线互相平分的四边形是平行四边形.布置作业课本第85页习题:第8~10题.再见!
