轴对称导学案(共五课时)
图片预览



文档简介
课题:第一课时10.1.1 生活中的轴对称
学习目标:
(1)通过生活中的轴对称现象,了解轴对称图形及轴对称的区别与联系;
(2)加深这两个概念的理解,能正确识别轴对称图形,培养观察能力;
(3)体会轴对称在现实生活中的广泛运用和它的美学价值;
重点、轴对称图形的概念.
难点:判断图形是否是轴对称图形。
一、新知准备自学:(学生自学教材,独立完成互评)时间:15分钟
1、观察一下书P8010.1.1中的图形,它们都是
图形,这些图形有什么特点呢?(让学生说一说)
2、轴对称图形的定义: 如果一个图形沿某条直线对折,对折两部分
,那么这个图形
,这条直线叫做这个图形的
。
3、画出书中图10.1.1中各图形的对称轴。是不是每一个轴对称图形都只有一条对称轴?答:
。
4、
轴对称的定义:
把一个图形沿着某一条直线翻折过去,如果它能够与
重合,那么就说这两个图形
,这条直线就是
,两个图形中的对应点(即两个图形重合时互相重合的点)叫做
。
5、轴对称图形和轴对称的区别与联系
区别:(1)轴对称图形是指一个具有特殊形状的图形,只对
个
图形而言;轴对称是指
个图形的位置的关系,必须涉及
个图形。(2)轴对称图形的对称轴
;轴对称只有
。
联系:(1)图中都有一条直线,都要沿着这条直线
。
(2)如果把两个成轴对称图形拼在一起,看成一个整体,那么它就是一个
。
如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成
。
(3)轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是
的,所以它的对应线段(对折后重合的线段)
,对应角(对折后重合的角)
。
二、探究、发现(学生分组讨论,展示小组结果)时间:10分钟
1、
如图是否为轴对称图形,若是请画出对称轴。
2、观察下图中各种图形,说出哪些图形可以放在一起形成轴对称(可以将图形上下放置或左右放置)
解:左右放置可以形成轴对称的有:(1)和(
),(2)和(
),(9)和(
);
上下放置可以形成轴对称的有:(2)和(
),(5
和(
),(7)和(
)。
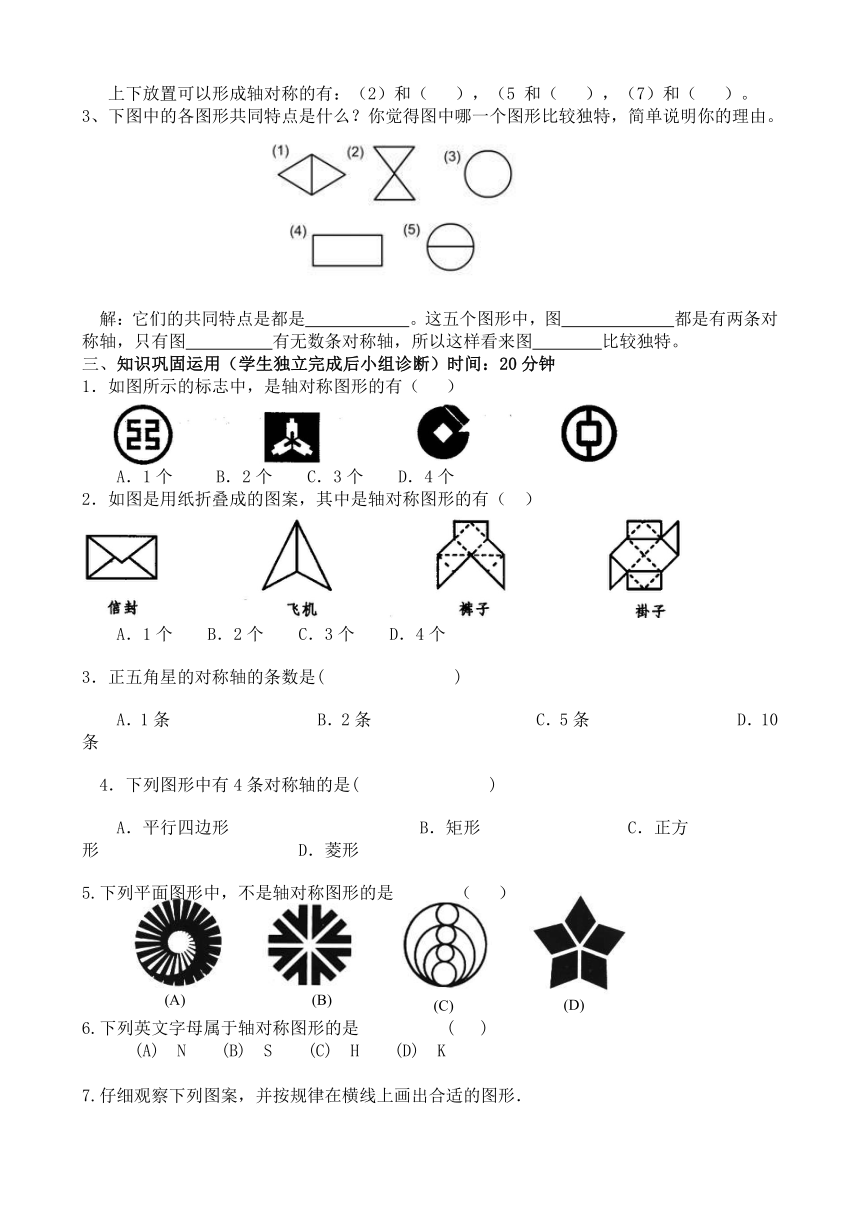
3、下图中的各图形共同特点是什么?你觉得图中哪一个图形比较独特,简单说明你的理由。
解:它们的共同特点是都是
。这五个图形中,图
都是有两条对称轴,只有图
有无数条对称轴,所以这样看来图
比较独特。
三、知识巩固运用(学生独立完成后小组诊断)时间:20分钟
1.如图所示的标志中,是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
2.如图是用纸折叠成的图案,其中是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
3.正五角星的对称轴的条数是(
)
A.1条
B.2条
C.5条
D.10条
4.下列图形中有4条对称轴的是(
)
A.平行四边形
B.矩形
C.正方形
D.菱形
5.下列平面图形中,不是轴对称图形的是
(
)
6.下列英文字母属于轴对称图形的是
(
)
(A)
N
(B)
S
(C)
H
(D)
K
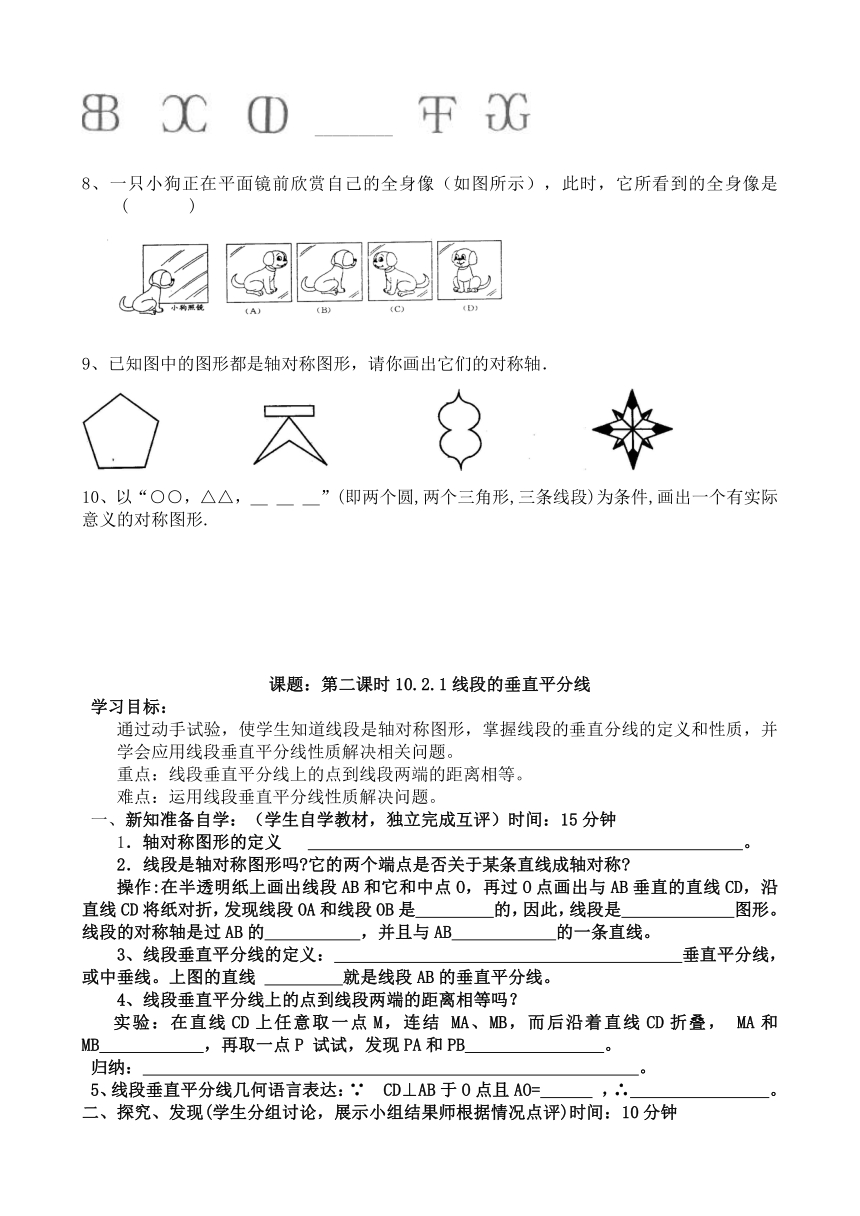
7.仔细观察下列图案,并按规律在横线上画出合适的图形.
_________
8、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是(
)
9、已知图中的图形都是轴对称图形,请你画出它们的对称轴.
10、以“○○,△△,_
_
_”(即两个圆,两个三角形,三条线段)为条件,画出一个有实际意义的对称图形.
课题:第二课时10.2.1线段的垂直平分线
学习目标:
通过动手试验,使学生知道线段是轴对称图形,掌握线段的垂直分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。
重点:线段垂直平分线上的点到线段两端的距离相等。
难点:运用线段垂直平分线性质解决问题。
一、新知准备自学:(学生自学教材,独立完成互评)时间:15分钟
1.轴对称图形的定义
。
2.线段是轴对称图形吗 它的两个端点是否关于某条直线成轴对称
操作:在半透明纸上画出线段AB和它和中点O,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折,发现线段OA和线段OB是
的,因此,线段是
图形。线段的对称轴是过AB的
,并且与AB
的一条直线。
3、线段垂直平分线的定义:
垂直平分线,或中垂线。上图的直线
就是线段AB的垂直平分线。
4、线段垂直平分线上的点到线段两端的距离相等吗?
实验:在直线CD上任意取一点M,连结
MA、MB,而后沿着直线CD折叠,
MA和MB
,再取一点P
试试,发现PA和PB
。
归纳:
。
5、线段垂直平分线几何语言表达:∵
CD⊥AB于O点且AO=
,∴
。
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:10分钟
问题1.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
分析:要求△BCE的周长,需知道
的长度,从题目给出的条件来看,
的长度已经知道,而
点是线段BC的垂直平分线上的点,所以
,从而问题得到解决。
解:
问题2.如右图所示,直线MN和DE分别是线段
AB、BC的垂直平分线,它们交于P点,请问PA和
PC相等吗 为什么
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:20分钟
1.点P是△ABC中边AB的垂直平分线上的点,则一定有(
)
A.PA=PB
B.PA=PC
C.PB=PC
D.点P到∠ACB的两边的距离相等
2.下列说法错误的是(
)
A.D、E是线段AB的垂直平分线上的两点,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是线段AB的垂直平分线
3.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
4.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是(
)
A.9
B.8
C.7
D.6
5.平面内到不在同一条直线的三个点A、B、C的距离相等的点有(
)
A.0个
B.1个
C.2个
D.3个
6.经过线段的___________________的直线,叫做这条线段的垂直平分线.
7.线段的垂直平分线上的点_______________________________;反过来,与一条线段两个端点距离相等的点在这条线段的____________________上,因此线段的垂直平分线可以看成___________________的点的集合.
8.如图,△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,则BC=_________.
9、如图2,△ABC中,AB=AC=18cm,BC=
10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
(拓展提高题选用):
1.如图,△BAC=120°,∠C=30°,DE是线段AC的垂直平分线,求:∠BAD的度数。
2、 如图
在△ABC中,AB
=
AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,求AB、BC。
如图,在△ABC中,AB的垂直平分线交AC于D,如果AC=
5cm,BC=
4cm,AE
=
2cm,求△CDB的周长。
A
课题:第三课时
简单的轴对称图形--角平分线
学习目标
使学生知道角是轴对称图形,对称轴是角平分线所在的直线,
掌握角平分线的性质,并能运用它解决相关问题。
重点:角平分线上的点到角两边的距离相等。
难点:运用角平分线性质解决问题。
一、新知准备自学:(学生自学教材,独立完成互评)时间:10分钟
1.点到直线的距离的定义是
。
2.角是轴对称图形吗 对称轴是哪一条直线
试验:在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM,从上面试验可以看出,角是
,对称轴是
。
3、角平分线的性质:上图中在射线OM上任取一点P,过P点分别作OA和OB的垂线段PC和PD,而后沿着OM折叠,可以发现PC和
PD
。
归纳:角平分线上的点到角两边的距离
.
4、几何语言表达:∵
,∴
。
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:12分钟
问题1.如下图所示,在△ABC中,∠C=
90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD与DC有什么数量关系 为什么
问题2.如上图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,求
P点到直线AB的距离。
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:23分钟
1、判断题
(1)角的平分线是角的对称轴.(
)
(2)等腰直角三角形不是轴对称图形.(
)
(3)等腰三角形底边上的高所在直线是它的对称轴.(
)
(4)射线是轴对称图形.(
)
(5)线段的垂直平分线是线段的一条对称轴.(
)
2、射线OC平分,点P在OC上,且于M,
PN垂直OB于N,且PM=2cm时,则PN=__________cm.
3、已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列
确定P点的方法正确的是(
)
A.P为∠A、∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为AC、AB两边上的高的交点
D.P为AC、AB两边的垂直平分线的交点
4、如图,AD平分∠BAC,∠C=90°,DE⊥
AB于E,那么(1)DE和DC相等吗 为什么
(2)AE和AC相等吗 为什么
5、在下面左图中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等。
课题:第四课时
10.2.2
画图形的对称轴
学习目标:
使学生掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并能熟练画出轴对称图形的对称轴。
重点:画轴对称图形的对称轴。
难点:归纳总结画轴对称图形对称轴的方法
一、新知准备自学:(学生自学教材,独立完成互评)时间:10分钟
1.轴对称图形指
。
2.看以下两个图形是否是轴对称图形 你能否画出它的对称轴
3
、
线段、角、等腰三角形
、等边三角形、菱形、长方形、正五边形的对称轴 各有几条?对称轴是怎样的直线?
答:
。
4、画出下面两个图形的对称轴。
5、对称轴的画法:(1)找出轴对称图形的任意一组
,连结
,(2)画对称点所连线段的
,就得到该图形的对称轴。
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:15分钟
问题1:画出以下图形的对称轴
问题2:下面的虚线,哪几条是图形的对称轴?
由问题1、问题2发现如果图形关于某一条直线对称,那么连结对称点的线段被对称轴
。
问题3:平面上的两条相交直线是轴对称图形吗?如果是,它有几条对称轴?画画试试看。.
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:20分钟
1、如图,若ΔABC与ΔDEF关于直线MN对称,点A和点D、点B和点E、点C和点F分别是对应点,则直线MN是线段BE的
, ΔABC与
重合.
2、如图,已知直线PM是ΔABP的对称轴,则
①
图中共有___对三角形重合;②
若∠
PAQ=25度,则
∠
PBQ=__度;③
若AM=3㎝,则BM=__㎝.
如图 ,直线MN是线段AB的对称轴,点C在直线MN外,CA与MN相交于点D,如果CA+CB=4㎝,那么ΔBCD的周长为_____㎝.
4、如图4,四边形ABCD是关于直线MN的轴对称图形,分别延长CB和DA相交于一点P,则点P在( )
(A)直线MN上 (B)直线MN外
(C)点P满足PD≠
PC
(D)以上答案均不对
5、如图5,直线CD是等腰三角形的对称轴,DE⊥
AB于E,∠
B=55度,则∠
CDE的度数为( ).
(A)55度 (B)35度 (C)45度 (D)30度
课题:第五课时
10.2.3画轴对称图形
学习目标:
1.使学生能够按要求作出简单平面图形经过一次对称后的图形。
2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。
重点:让学生识别轴对称图形与画轴对称图形的对称轴。
难点:区别轴对称与轴对称图形两个不同的概念。
一、新知准备自学:(学生自学教材,独立完成互评)时间:15分钟
1、
叫做轴对称图形。
2、
如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢
请同学们尝试解决以下问题:如图(1),(2)实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形。
3、如图,已知点A和L直线,试画出点A关于直线l的对称点A′。
L
A·
4、请你画出图中A、B、C三点关于直线l的对称点。
A
B
C
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:15分钟
1.已知△ABC,直线L,画出△ABC关于直线L的对称图形。
A
B C
2、在图中分别画出点A关于两条直线的对称点和点.
3、
画出所示图形关于直线的对称图形.
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:15分钟
1、填空:(1)、圆有
对称轴。(2)、正方形有
条对称轴,长方形有
条对称轴,等腰三角形有
条对称轴,等边三角形有
条对称轴。
2、如图,分别以AB为对称轴,画出各图形的对称图形,并观察图形(3)和它的轴对称图形构成一个
三角形.
3、一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是
。
4、星期天小华去书店买书时,从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示,此时时针表示的时间是
。
5、下列图形中,是轴对称图形的是(
)
6、画出所给图形的轴对称图形。
7、从A地到河边取水后返回B地,如何走路程最短?请作图示意。
(A)
(B)
(C)
(D)
1题图
2题
3题
图5
图4
L
L
B
A
B
A
学习目标:
(1)通过生活中的轴对称现象,了解轴对称图形及轴对称的区别与联系;
(2)加深这两个概念的理解,能正确识别轴对称图形,培养观察能力;
(3)体会轴对称在现实生活中的广泛运用和它的美学价值;
重点、轴对称图形的概念.
难点:判断图形是否是轴对称图形。
一、新知准备自学:(学生自学教材,独立完成互评)时间:15分钟
1、观察一下书P8010.1.1中的图形,它们都是
图形,这些图形有什么特点呢?(让学生说一说)
2、轴对称图形的定义: 如果一个图形沿某条直线对折,对折两部分
,那么这个图形
,这条直线叫做这个图形的
。
3、画出书中图10.1.1中各图形的对称轴。是不是每一个轴对称图形都只有一条对称轴?答:
。
4、
轴对称的定义:
把一个图形沿着某一条直线翻折过去,如果它能够与
重合,那么就说这两个图形
,这条直线就是
,两个图形中的对应点(即两个图形重合时互相重合的点)叫做
。
5、轴对称图形和轴对称的区别与联系
区别:(1)轴对称图形是指一个具有特殊形状的图形,只对
个
图形而言;轴对称是指
个图形的位置的关系,必须涉及
个图形。(2)轴对称图形的对称轴
;轴对称只有
。
联系:(1)图中都有一条直线,都要沿着这条直线
。
(2)如果把两个成轴对称图形拼在一起,看成一个整体,那么它就是一个
。
如果把轴对称图形沿对称轴分成两部分,那么这两个图形就关于这条直线成
。
(3)轴对称图形(或关于某条直线对称的两个图形)沿对称轴对折后的两部分是
的,所以它的对应线段(对折后重合的线段)
,对应角(对折后重合的角)
。
二、探究、发现(学生分组讨论,展示小组结果)时间:10分钟
1、
如图是否为轴对称图形,若是请画出对称轴。
2、观察下图中各种图形,说出哪些图形可以放在一起形成轴对称(可以将图形上下放置或左右放置)
解:左右放置可以形成轴对称的有:(1)和(
),(2)和(
),(9)和(
);
上下放置可以形成轴对称的有:(2)和(
),(5
和(
),(7)和(
)。
3、下图中的各图形共同特点是什么?你觉得图中哪一个图形比较独特,简单说明你的理由。
解:它们的共同特点是都是
。这五个图形中,图
都是有两条对称轴,只有图
有无数条对称轴,所以这样看来图
比较独特。
三、知识巩固运用(学生独立完成后小组诊断)时间:20分钟
1.如图所示的标志中,是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
2.如图是用纸折叠成的图案,其中是轴对称图形的有(
)
A.1个
B.2个
C.3个
D.4个
3.正五角星的对称轴的条数是(
)
A.1条
B.2条
C.5条
D.10条
4.下列图形中有4条对称轴的是(
)
A.平行四边形
B.矩形
C.正方形
D.菱形
5.下列平面图形中,不是轴对称图形的是
(
)
6.下列英文字母属于轴对称图形的是
(
)
(A)
N
(B)
S
(C)
H
(D)
K
7.仔细观察下列图案,并按规律在横线上画出合适的图形.
_________
8、一只小狗正在平面镜前欣赏自己的全身像(如图所示),此时,它所看到的全身像是(
)
9、已知图中的图形都是轴对称图形,请你画出它们的对称轴.
10、以“○○,△△,_
_
_”(即两个圆,两个三角形,三条线段)为条件,画出一个有实际意义的对称图形.
课题:第二课时10.2.1线段的垂直平分线
学习目标:
通过动手试验,使学生知道线段是轴对称图形,掌握线段的垂直分线的定义和性质,并学会应用线段垂直平分线性质解决相关问题。
重点:线段垂直平分线上的点到线段两端的距离相等。
难点:运用线段垂直平分线性质解决问题。
一、新知准备自学:(学生自学教材,独立完成互评)时间:15分钟
1.轴对称图形的定义
。
2.线段是轴对称图形吗 它的两个端点是否关于某条直线成轴对称
操作:在半透明纸上画出线段AB和它和中点O,再过O点画出与AB垂直的直线CD,沿直线CD将纸对折,发现线段OA和线段OB是
的,因此,线段是
图形。线段的对称轴是过AB的
,并且与AB
的一条直线。
3、线段垂直平分线的定义:
垂直平分线,或中垂线。上图的直线
就是线段AB的垂直平分线。
4、线段垂直平分线上的点到线段两端的距离相等吗?
实验:在直线CD上任意取一点M,连结
MA、MB,而后沿着直线CD折叠,
MA和MB
,再取一点P
试试,发现PA和PB
。
归纳:
。
5、线段垂直平分线几何语言表达:∵
CD⊥AB于O点且AO=
,∴
。
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:10分钟
问题1.如右图所示,△ABC中,BC=10,边BC的垂直平分线分别交AB、BC于点E、D,BE=6,求△BCE的周长。
分析:要求△BCE的周长,需知道
的长度,从题目给出的条件来看,
的长度已经知道,而
点是线段BC的垂直平分线上的点,所以
,从而问题得到解决。
解:
问题2.如右图所示,直线MN和DE分别是线段
AB、BC的垂直平分线,它们交于P点,请问PA和
PC相等吗 为什么
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:20分钟
1.点P是△ABC中边AB的垂直平分线上的点,则一定有(
)
A.PA=PB
B.PA=PC
C.PB=PC
D.点P到∠ACB的两边的距离相等
2.下列说法错误的是(
)
A.D、E是线段AB的垂直平分线上的两点,则AD=BD,AE=BE
B.若AD=BD,AE=BE,则直线DE是线段AB的垂直平分线
C.若PA=PB,则点P在线段AB的垂直平分线上
D.若PA=PB,则过点P的直线是线段AB的垂直平分线
3.在锐角△ABC内一点P满足PA=PB=PC,则点P是△ABC(
)
A.三条角平分线的交点
B.三条中线的交点
C.三条高的交点
D.三边垂直平分线的交点
4.△ABC中AC>BC,边AB的垂直平分线与AC交于点D,已知AC=5,BC=4,则△BCD的周长是(
)
A.9
B.8
C.7
D.6
5.平面内到不在同一条直线的三个点A、B、C的距离相等的点有(
)
A.0个
B.1个
C.2个
D.3个
6.经过线段的___________________的直线,叫做这条线段的垂直平分线.
7.线段的垂直平分线上的点_______________________________;反过来,与一条线段两个端点距离相等的点在这条线段的____________________上,因此线段的垂直平分线可以看成___________________的点的集合.
8.如图,△ABC中,AB=AC=14cm,D是AB的中点,DE⊥AB于D交AC于E,△EBC的周长是24cm,则BC=_________.
9、如图2,△ABC中,AB=AC=18cm,BC=
10cm,AB的垂直平分线ED交AC于D点,求:△BCD的周长。
(拓展提高题选用):
1.如图,△BAC=120°,∠C=30°,DE是线段AC的垂直平分线,求:∠BAD的度数。
2、 如图
在△ABC中,AB
=
AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60cm和38cm,求AB、BC。
如图,在△ABC中,AB的垂直平分线交AC于D,如果AC=
5cm,BC=
4cm,AE
=
2cm,求△CDB的周长。
A
课题:第三课时
简单的轴对称图形--角平分线
学习目标
使学生知道角是轴对称图形,对称轴是角平分线所在的直线,
掌握角平分线的性质,并能运用它解决相关问题。
重点:角平分线上的点到角两边的距离相等。
难点:运用角平分线性质解决问题。
一、新知准备自学:(学生自学教材,独立完成互评)时间:10分钟
1.点到直线的距离的定义是
。
2.角是轴对称图形吗 对称轴是哪一条直线
试验:在半透明的纸上画∠AOB,对折,使角的两条边完全重合,然后用直尺画出折痕OM,从上面试验可以看出,角是
,对称轴是
。
3、角平分线的性质:上图中在射线OM上任取一点P,过P点分别作OA和OB的垂线段PC和PD,而后沿着OM折叠,可以发现PC和
PD
。
归纳:角平分线上的点到角两边的距离
.
4、几何语言表达:∵
,∴
。
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:12分钟
问题1.如下图所示,在△ABC中,∠C=
90°,BD是角平分线,交AC于点D,DE⊥AB,垂足为点E,AD=3DE。AD与DC有什么数量关系 为什么
问题2.如上图,BD垂直平分线段AC,AE⊥BC,垂足为E,交BD于P点,PE=3cm,求
P点到直线AB的距离。
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:23分钟
1、判断题
(1)角的平分线是角的对称轴.(
)
(2)等腰直角三角形不是轴对称图形.(
)
(3)等腰三角形底边上的高所在直线是它的对称轴.(
)
(4)射线是轴对称图形.(
)
(5)线段的垂直平分线是线段的一条对称轴.(
)
2、射线OC平分,点P在OC上,且于M,
PN垂直OB于N,且PM=2cm时,则PN=__________cm.
3、已知△ABC,求作一点P,使P到∠A的两边的距离相等,且PA=PB.下列
确定P点的方法正确的是(
)
A.P为∠A、∠B两角平分线的交点
B.P为∠A的角平分线与AB的垂直平分线的交点
C.P为AC、AB两边上的高的交点
D.P为AC、AB两边的垂直平分线的交点
4、如图,AD平分∠BAC,∠C=90°,DE⊥
AB于E,那么(1)DE和DC相等吗 为什么
(2)AE和AC相等吗 为什么
5、在下面左图中找出点A,使它到M,N两点的距离相等,并且到OH,OF的距离相等。
课题:第四课时
10.2.2
画图形的对称轴
学习目标:
使学生掌握用“连结对称点的线段被对称轴垂直平分”验证一个图形是不是轴对称图形,并能熟练画出轴对称图形的对称轴。
重点:画轴对称图形的对称轴。
难点:归纳总结画轴对称图形对称轴的方法
一、新知准备自学:(学生自学教材,独立完成互评)时间:10分钟
1.轴对称图形指
。
2.看以下两个图形是否是轴对称图形 你能否画出它的对称轴
3
、
线段、角、等腰三角形
、等边三角形、菱形、长方形、正五边形的对称轴 各有几条?对称轴是怎样的直线?
答:
。
4、画出下面两个图形的对称轴。
5、对称轴的画法:(1)找出轴对称图形的任意一组
,连结
,(2)画对称点所连线段的
,就得到该图形的对称轴。
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:15分钟
问题1:画出以下图形的对称轴
问题2:下面的虚线,哪几条是图形的对称轴?
由问题1、问题2发现如果图形关于某一条直线对称,那么连结对称点的线段被对称轴
。
问题3:平面上的两条相交直线是轴对称图形吗?如果是,它有几条对称轴?画画试试看。.
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:20分钟
1、如图,若ΔABC与ΔDEF关于直线MN对称,点A和点D、点B和点E、点C和点F分别是对应点,则直线MN是线段BE的
, ΔABC与
重合.
2、如图,已知直线PM是ΔABP的对称轴,则
①
图中共有___对三角形重合;②
若∠
PAQ=25度,则
∠
PBQ=__度;③
若AM=3㎝,则BM=__㎝.
如图 ,直线MN是线段AB的对称轴,点C在直线MN外,CA与MN相交于点D,如果CA+CB=4㎝,那么ΔBCD的周长为_____㎝.
4、如图4,四边形ABCD是关于直线MN的轴对称图形,分别延长CB和DA相交于一点P,则点P在( )
(A)直线MN上 (B)直线MN外
(C)点P满足PD≠
PC
(D)以上答案均不对
5、如图5,直线CD是等腰三角形的对称轴,DE⊥
AB于E,∠
B=55度,则∠
CDE的度数为( ).
(A)55度 (B)35度 (C)45度 (D)30度
课题:第五课时
10.2.3画轴对称图形
学习目标:
1.使学生能够按要求作出简单平面图形经过一次对称后的图形。
2.通过画轴对称图形,增强学生学习几何的趣味感,培养审美情操。
重点:让学生识别轴对称图形与画轴对称图形的对称轴。
难点:区别轴对称与轴对称图形两个不同的概念。
一、新知准备自学:(学生自学教材,独立完成互评)时间:15分钟
1、
叫做轴对称图形。
2、
如果有一个图形、一条直线,那么如何画出这个图形关于这条直线的对称图形呢
请同学们尝试解决以下问题:如图(1),(2)实线所构成的图形为已知图形,虚线为对称轴,请画出已知图形的轴对称图形。
在格点图中,大家会很容易地画出已知图形的轴对称图形,如果没有格点图,我们还能比较准确地画出已知图形的轴对称图形。
3、如图,已知点A和L直线,试画出点A关于直线l的对称点A′。
L
A·
4、请你画出图中A、B、C三点关于直线l的对称点。
A
B
C
二、探究、发现(学生分组讨论,展示小组结果师根据情况点评)时间:15分钟
1.已知△ABC,直线L,画出△ABC关于直线L的对称图形。
A
B C
2、在图中分别画出点A关于两条直线的对称点和点.
3、
画出所示图形关于直线的对称图形.
三、知识巩固运用(学生独立完成后小组诊断师根据情况点评)时间:15分钟
1、填空:(1)、圆有
对称轴。(2)、正方形有
条对称轴,长方形有
条对称轴,等腰三角形有
条对称轴,等边三角形有
条对称轴。
2、如图,分别以AB为对称轴,画出各图形的对称图形,并观察图形(3)和它的轴对称图形构成一个
三角形.
3、一交警在执勤过程中,从汽车的后视镜中看见某车牌照的后5位号码是,该车牌的后5位号码实际是
。
4、星期天小华去书店买书时,从镜子内看到背后墙上普通时钟的时针(粗)与分针(细)的位置如图所示,此时时针表示的时间是
。
5、下列图形中,是轴对称图形的是(
)
6、画出所给图形的轴对称图形。
7、从A地到河边取水后返回B地,如何走路程最短?请作图示意。
(A)
(B)
(C)
(D)
1题图
2题
3题
图5
图4
L
L
B
A
B
A
