初中数学苏科版八下聚焦《匀股定理》中的数学思想 教学案(含答案)
文档属性
| 名称 | 初中数学苏科版八下聚焦《匀股定理》中的数学思想 教学案(含答案) | 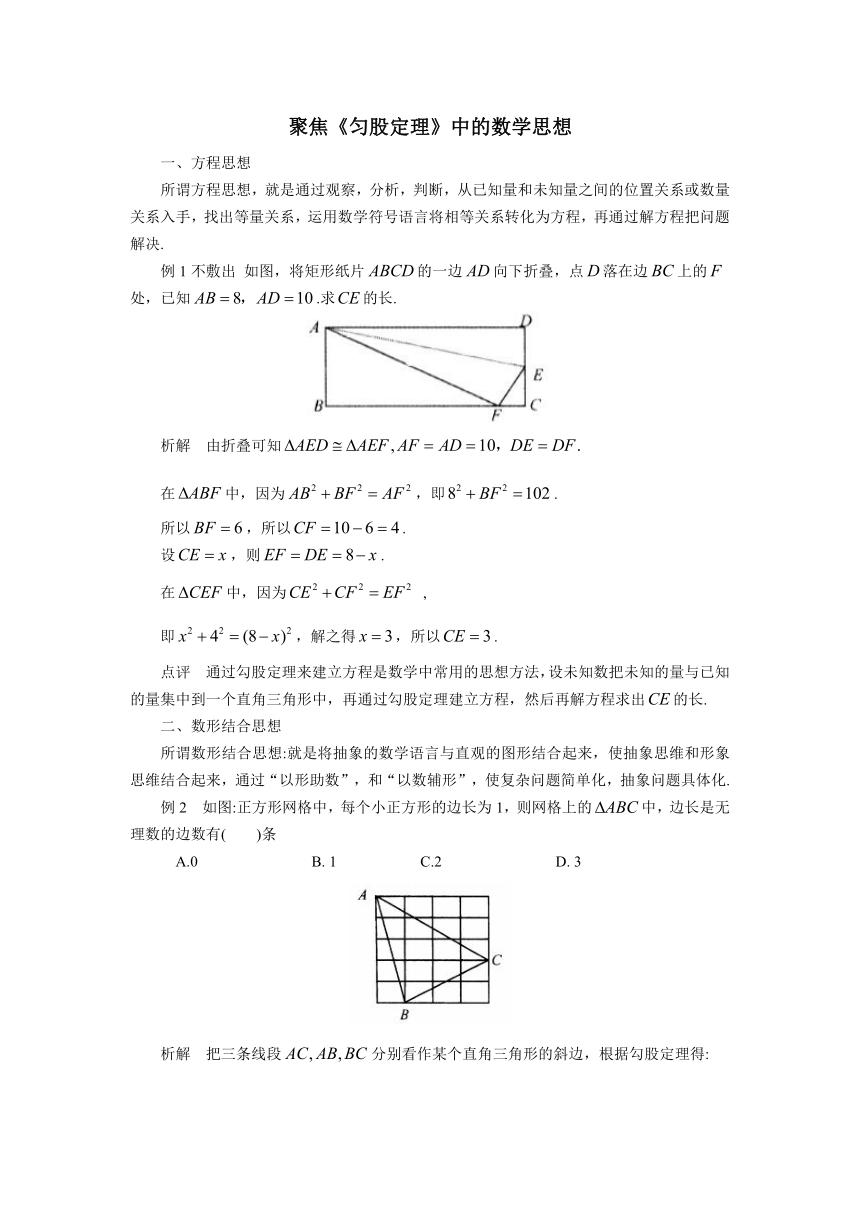 | |
| 格式 | zip | ||
| 文件大小 | 205.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-19 18:11:33 | ||
图片预览

文档简介
聚焦《匀股定理》中的数学思想
一、方程思想
所谓方程思想,就是通过观察,分析,判断,从已知量和未知量之间的位置关系或数量关系入手,找出等量关系,运用数学符号语言将相等关系转化为方程,再通过解方程把问题解决.
例1不敷出
如图,将矩形纸片的一边向下折叠,点落在边上的
处,已知.求的长.
析解
由折叠可知
在中,因为,即.
所以,所以.
设,则.
在中,因为
,
即,解之得,所以.
点评
通过勾股定理来建立方程是数学中常用的思想方法,设未知数把未知的量与已知的量集中到一个直角三角形中,再通过勾股定理建立方程,然后再解方程求出的长.
二、数形结合思想
所谓数形结合思想:就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,通过“以形助数”,和“以数辅形”,使复杂问题简单化,抽象问题具体化.
例2
如图:正方形网格中,每个小正方形的边长为1,则网格上的中,边长是无理数的边数有(
)条
A.0
B.
1
C.2
D.
3
析解
把三条线段分别看作某个直角三角形的斜边,根据勾股定理得:
因为的长为无理数,故选C.
点评
勾股定理由已知的“直角三角形”得出“”的结论,这是由“形”的条件而得出“数”的结果,蕴含着从形到数的转化.
三、分类讨论思想
所谓分类讨论思想,就是将问题划分为若干个既不重复也不遗漏的小问题,再一一加以解决的方法.当问题的条件不具体时,通过分类讨论可以确定准确的答案.
例3
在中,,边上的高.求的面积.
析解
因为的形状不确定,需要分类讨论.
(1)当是锐角三角形时在中,,即,所以.
在直角中,,
即,所以.
所以.
所以
(2)当是钝角三角形时:
在直角中,,
即,所以.
在直角中,,
即,所以.所以,
所以.
综上所述,
的面积为84或24.
点评
本题的形状不确定,可以通过分类讨论来解决问题.
四、转化思想
所谓转化思想,就是将要解决的问题转化为另一个较为容易解决的问题或已经解决的问题,具体的做法是将未知的“转化”为“已知”,将“陌生”的转化为“熟悉”,将“复杂”的转化为“简单”.
例4
如图:要在直线上修一水利站,分别向张庄和
李庄送水,已知张庄到河边的距离=
2km,李庄
到河边的距离=7km,
=12km.如果铺设水管的工
程费用为每千米1500元,求铺设水管的最小费用.
析解
求铺设水管的费用最小,就是转化为求铺设水管长度最短.延长到,使,连接交于点,此时最小.过点作交的
延长线于点,根据题意得:,所以,,
在直角中,,所以.因为,即的最小值为15,所以铺设水管的最少费用为15
×1500
=
22500元.
点评
遇到实际问题或非直角三角形时,通常把实际问题或非直角三角形转化为直角三角形,然后利用勾股定理来解决问题.
一、方程思想
所谓方程思想,就是通过观察,分析,判断,从已知量和未知量之间的位置关系或数量关系入手,找出等量关系,运用数学符号语言将相等关系转化为方程,再通过解方程把问题解决.
例1不敷出
如图,将矩形纸片的一边向下折叠,点落在边上的
处,已知.求的长.
析解
由折叠可知
在中,因为,即.
所以,所以.
设,则.
在中,因为
,
即,解之得,所以.
点评
通过勾股定理来建立方程是数学中常用的思想方法,设未知数把未知的量与已知的量集中到一个直角三角形中,再通过勾股定理建立方程,然后再解方程求出的长.
二、数形结合思想
所谓数形结合思想:就是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合起来,通过“以形助数”,和“以数辅形”,使复杂问题简单化,抽象问题具体化.
例2
如图:正方形网格中,每个小正方形的边长为1,则网格上的中,边长是无理数的边数有(
)条
A.0
B.
1
C.2
D.
3
析解
把三条线段分别看作某个直角三角形的斜边,根据勾股定理得:
因为的长为无理数,故选C.
点评
勾股定理由已知的“直角三角形”得出“”的结论,这是由“形”的条件而得出“数”的结果,蕴含着从形到数的转化.
三、分类讨论思想
所谓分类讨论思想,就是将问题划分为若干个既不重复也不遗漏的小问题,再一一加以解决的方法.当问题的条件不具体时,通过分类讨论可以确定准确的答案.
例3
在中,,边上的高.求的面积.
析解
因为的形状不确定,需要分类讨论.
(1)当是锐角三角形时在中,,即,所以.
在直角中,,
即,所以.
所以.
所以
(2)当是钝角三角形时:
在直角中,,
即,所以.
在直角中,,
即,所以.所以,
所以.
综上所述,
的面积为84或24.
点评
本题的形状不确定,可以通过分类讨论来解决问题.
四、转化思想
所谓转化思想,就是将要解决的问题转化为另一个较为容易解决的问题或已经解决的问题,具体的做法是将未知的“转化”为“已知”,将“陌生”的转化为“熟悉”,将“复杂”的转化为“简单”.
例4
如图:要在直线上修一水利站,分别向张庄和
李庄送水,已知张庄到河边的距离=
2km,李庄
到河边的距离=7km,
=12km.如果铺设水管的工
程费用为每千米1500元,求铺设水管的最小费用.
析解
求铺设水管的费用最小,就是转化为求铺设水管长度最短.延长到,使,连接交于点,此时最小.过点作交的
延长线于点,根据题意得:,所以,,
在直角中,,所以.因为,即的最小值为15,所以铺设水管的最少费用为15
×1500
=
22500元.
点评
遇到实际问题或非直角三角形时,通常把实际问题或非直角三角形转化为直角三角形,然后利用勾股定理来解决问题.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
