初中数学苏科版八下完美补图精彩解题 教学案(含答案)
文档属性
| 名称 | 初中数学苏科版八下完美补图精彩解题 教学案(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-19 00:00:00 | ||
图片预览

文档简介
完美补图
精彩解题
解题中,对于比较复杂或不太规则的图形,我们常需要将它分割成规则的熟悉的图形,但有时仍然不容易找到思路,这时可考虑换一个角度,通过补图达到化难为易的目的.补形法是几何解题中的一种重要方法,现以几个经典题为例说明如下.
一、补成特殊的三角形
遇到题中有角平分线,垂线,中线中的两个作为条件同时出现,可考虑将图形补为等
腰三角形.
例1
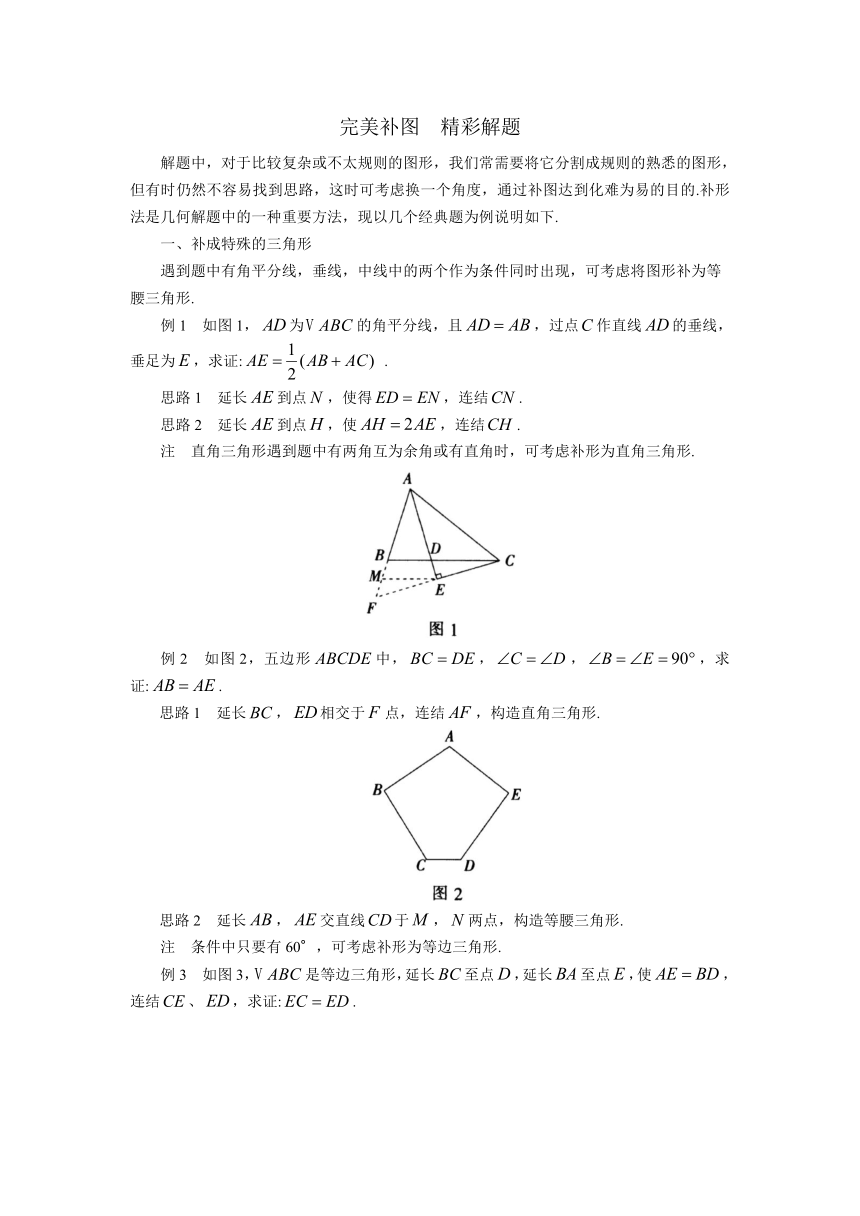
如图1,为的角平分线,且,过点作直线的垂线,垂足为,求证:
.
思路1
延长到点,使得,连结.
思路2
延长到点,使,连结.
注
直角三角形遇到题中有两角互为余角或有直角时,可考虑补形为直角三角形.
例2
如图2,五边形中,,,,求证:.
思路1
延长,相交于点,连结,构造直角三角形.
思路2
延长,交直线于,两点,构造等腰三角形.
注
条件中只要有60°,可考虑补形为等边三角形.
例3
如图3,是等边三角形,延长至点,延长至点,使,连结、,求证:.
思路1
过点作垂直于点,利用30°直角三角形的特殊性质.
思路2
过点作平行交延长线于点.
二、补形为四边形
1.遇到菱形的判定条件(如两邻边相等)时,可考虑补形为菱形.
例4
如图4,在五边形中,,,,,,求五边形的周长.
思路
过点、分别作,的垂线交于,两点.
2.遇到矩形的判定条件如有三个直角等时,可考虑补为长方形.
例5
如图5,三个正方形连续紧靠着,它们的边长依次记为,,,则图中的面积为
.(用,,的代数式表示)
思路
先利用相似三角形性质求两个三角形的公共底.
3.遇到等腰直角三角形时,可考虑补形为正方形.
例6
如图6,在中,,,是中点,于点,延长线交于点,求证:.
思路1
过,作的垂线,垂足为,,先证.
思路2
过点作于点,交于点,先证,再证.
三、补形为圆
遇到对角互补的四边形,同底同侧相等的三角形等条件时,可考虑补作圆.
例7
如图7,在中,高、相交于点,且,为内的一点,且,,连结,求证:平分.
思路1
计算得,,,,四点共圆,故.
思路2
计算得,设,交点为M,,再证,故.
精彩解题
解题中,对于比较复杂或不太规则的图形,我们常需要将它分割成规则的熟悉的图形,但有时仍然不容易找到思路,这时可考虑换一个角度,通过补图达到化难为易的目的.补形法是几何解题中的一种重要方法,现以几个经典题为例说明如下.
一、补成特殊的三角形
遇到题中有角平分线,垂线,中线中的两个作为条件同时出现,可考虑将图形补为等
腰三角形.
例1
如图1,为的角平分线,且,过点作直线的垂线,垂足为,求证:
.
思路1
延长到点,使得,连结.
思路2
延长到点,使,连结.
注
直角三角形遇到题中有两角互为余角或有直角时,可考虑补形为直角三角形.
例2
如图2,五边形中,,,,求证:.
思路1
延长,相交于点,连结,构造直角三角形.
思路2
延长,交直线于,两点,构造等腰三角形.
注
条件中只要有60°,可考虑补形为等边三角形.
例3
如图3,是等边三角形,延长至点,延长至点,使,连结、,求证:.
思路1
过点作垂直于点,利用30°直角三角形的特殊性质.
思路2
过点作平行交延长线于点.
二、补形为四边形
1.遇到菱形的判定条件(如两邻边相等)时,可考虑补形为菱形.
例4
如图4,在五边形中,,,,,,求五边形的周长.
思路
过点、分别作,的垂线交于,两点.
2.遇到矩形的判定条件如有三个直角等时,可考虑补为长方形.
例5
如图5,三个正方形连续紧靠着,它们的边长依次记为,,,则图中的面积为
.(用,,的代数式表示)
思路
先利用相似三角形性质求两个三角形的公共底.
3.遇到等腰直角三角形时,可考虑补形为正方形.
例6
如图6,在中,,,是中点,于点,延长线交于点,求证:.
思路1
过,作的垂线,垂足为,,先证.
思路2
过点作于点,交于点,先证,再证.
三、补形为圆
遇到对角互补的四边形,同底同侧相等的三角形等条件时,可考虑补作圆.
例7
如图7,在中,高、相交于点,且,为内的一点,且,,连结,求证:平分.
思路1
计算得,,,,四点共圆,故.
思路2
计算得,设,交点为M,,再证,故.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
