8.2.1用代入法解二元一次方程组 课件
图片预览








文档简介
课件20张PPT。 8.2消元—二元一次方程组的解法
口 答 题380202课前练习:1.二元一次方程x+y=7
(1)用x的代数式表示y
(2)用y的代数式表示xy=7-xx=7-y温故而知新1、用含x的代数式表示y:
x + y = 22
2、用含y的代数式表示x:
2x - 7y = 8
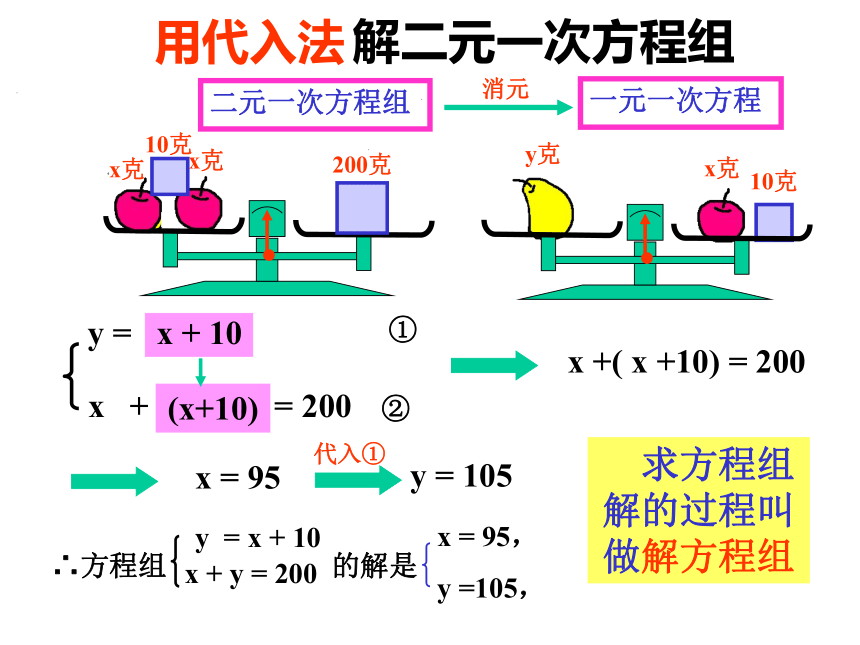
x + y = 200y = x + 10解二元一次方程组一元一次方程二元一次方程组消元用代入法x克10克(x+10)x +( x +10) = 200①②x = 95代入①y = 105 求方程组解的过程叫做解方程组例1 解方程组解:①②把②代入①得:2y – 3(y – 1)= 12y – 3y + 3 = 12y – 3y = 1 - 3- y = - 2 y = 2把y = 2代入②,得x = y – 1= 2 – 1= 1∴x = 1y = 22 y – 3 x = 1x = y - 1例1 解方程组解:①②把②代入①得:2y – 3(y – 1)= 12y – 3y + 3 = 12y – 3y = 1 - 3- y = - 2 y = 2把y = 2代入②,得x = y – 1= 2 – 1= 1∴x = 1y = 2练 习 题1、 解方程组例2 解方程组解:①②由②得:y = 1 – 2x③把③代入①得:3x – 2(1 – 2x)= 193x – 2 + 4x = 193x + 4x = 19 + 27x = 21x = 3把x = 3代入③,得y = 1 – 2x= 1 - 2×3= - 5∴x = 3y = - 51、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值4、写解例1 解方程组解:①②由②得:y = 1 – 2x③把③代入①得:3x – 2(1 – 2x)= 193x – 2 + 4x = 193x + 4x = 19 + 27x = 21x = 3把x = 3代入③,得y = 1 – 2x= 1 - 2×3= - 5∴x = 3y = - 5练 习 题 解方程组再练习:你解对了吗?1、用代入消元法解下列方程组例2 学以致用解:设这些消毒液应该分装x大瓶、y小瓶。根据题意可列方程组:解得:x=20000答:这些消毒液应该分装20000大瓶和50000小瓶。 根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),两种产品的销售数量(按瓶计算)的比为 某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
解: 2x = 8+7y即 ③ 把③代入②,得 解方程组∴ 方程组的解是 由①,得 可由方程①用一个未知数的代数式表示另一未知数,再代入另一方程!用代入法解方程组:(1) 2x+3y=40 ① 3x -2y=-5 ② ①②1、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.解:由题意知,①②由①得:y = 2 – 3x把③代入得:③5x + 2(2 – 3x)- 2 = 05x + 4 – 6x – 2 = 05x – 6x = 2 - 4-x = -2x = 2把x = 2 代入③,得: y= 2 - 3×2y= -4即x 的值是2,y 的值是-4.能力检测 2、若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.解:根据已知条件可列方程组:2m + n = 13m – 2n = 1①②由①得:把③代入②得:n = 1 –2m③3m – 2(1 – 2m)= 13m – 2 + 4m = 17m = 3提高巩固1.解下列二元一次方程组你认为怎样代入更简便? 请用你最简便的方法解出它的解。你的思路能解另一题吗?x+1=2(y-1)
3(x+1)=5(y-1)①
②⑴1.解下列二元一次方程组可将(x+1)、(y-1)看作一个整体求解。 解: 把①代入② 3×2(y-1)= 5(y-1) + 4 6(y-1) =5(y-1)+4 (y-1) = 4 ③ ∴ y = 5 把③代入①x +1 = 2×4∴ x = 7 〖分析〗=8 得 得:①
②3x+2y=13
x - 2y = 5⑵2.解下列二元一次方程组〖分析〗 可将2y看作一个数来求解。 解: 由②得:把③代入① 3x + (x – 5) = 13 4x = 18 ∴ x = 4.5把x = 4.5代入③2y = 4.5 – 5 = – 0.5 ∴ y = -0.25 2y = x – 5 ③ 得: 得: 拓展练习小结适用于未知数的系数为1或-11、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值4、写解
(1)用x的代数式表示y
(2)用y的代数式表示xy=7-xx=7-y温故而知新1、用含x的代数式表示y:
x + y = 22
2、用含y的代数式表示x:
2x - 7y = 8
x + y = 200y = x + 10解二元一次方程组一元一次方程二元一次方程组消元用代入法x克10克(x+10)x +( x +10) = 200①②x = 95代入①y = 105 求方程组解的过程叫做解方程组例1 解方程组解:①②把②代入①得:2y – 3(y – 1)= 12y – 3y + 3 = 12y – 3y = 1 - 3- y = - 2 y = 2把y = 2代入②,得x = y – 1= 2 – 1= 1∴x = 1y = 22 y – 3 x = 1x = y - 1例1 解方程组解:①②把②代入①得:2y – 3(y – 1)= 12y – 3y + 3 = 12y – 3y = 1 - 3- y = - 2 y = 2把y = 2代入②,得x = y – 1= 2 – 1= 1∴x = 1y = 2练 习 题1、 解方程组例2 解方程组解:①②由②得:y = 1 – 2x③把③代入①得:3x – 2(1 – 2x)= 193x – 2 + 4x = 193x + 4x = 19 + 27x = 21x = 3把x = 3代入③,得y = 1 – 2x= 1 - 2×3= - 5∴x = 3y = - 51、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值4、写解例1 解方程组解:①②由②得:y = 1 – 2x③把③代入①得:3x – 2(1 – 2x)= 193x – 2 + 4x = 193x + 4x = 19 + 27x = 21x = 3把x = 3代入③,得y = 1 – 2x= 1 - 2×3= - 5∴x = 3y = - 5练 习 题 解方程组再练习:你解对了吗?1、用代入消元法解下列方程组例2 学以致用解:设这些消毒液应该分装x大瓶、y小瓶。根据题意可列方程组:解得:x=20000答:这些消毒液应该分装20000大瓶和50000小瓶。 根据市场调查,某种消毒液的大瓶装(500g)和小瓶装(250g),两种产品的销售数量(按瓶计算)的比为 某厂每天生产这种消毒液22.5吨,这些消毒液应该分装大、小瓶两种产品各多少瓶?
解: 2x = 8+7y即 ③ 把③代入②,得 解方程组∴ 方程组的解是 由①,得 可由方程①用一个未知数的代数式表示另一未知数,再代入另一方程!用代入法解方程组:(1) 2x+3y=40 ① 3x -2y=-5 ② ①②1、如果∣y + 3x - 2∣+∣5x + 2y -2∣= 0,求 x 、y 的值.解:由题意知,①②由①得:y = 2 – 3x把③代入得:③5x + 2(2 – 3x)- 2 = 05x + 4 – 6x – 2 = 05x – 6x = 2 - 4-x = -2x = 2把x = 2 代入③,得: y= 2 - 3×2y= -4即x 的值是2,y 的值是-4.能力检测 2、若方程5x 2m+n + 4y 3m-2n = 9是关于x、y的二元一次方程,求m 、n 的值.解:根据已知条件可列方程组:2m + n = 13m – 2n = 1①②由①得:把③代入②得:n = 1 –2m③3m – 2(1 – 2m)= 13m – 2 + 4m = 17m = 3提高巩固1.解下列二元一次方程组你认为怎样代入更简便? 请用你最简便的方法解出它的解。你的思路能解另一题吗?x+1=2(y-1)
3(x+1)=5(y-1)①
②⑴1.解下列二元一次方程组可将(x+1)、(y-1)看作一个整体求解。 解: 把①代入② 3×2(y-1)= 5(y-1) + 4 6(y-1) =5(y-1)+4 (y-1) = 4 ③ ∴ y = 5 把③代入①x +1 = 2×4∴ x = 7 〖分析〗=8 得 得:①
②3x+2y=13
x - 2y = 5⑵2.解下列二元一次方程组〖分析〗 可将2y看作一个数来求解。 解: 由②得:把③代入① 3x + (x – 5) = 13 4x = 18 ∴ x = 4.5把x = 4.5代入③2y = 4.5 – 5 = – 0.5 ∴ y = -0.25 2y = x – 5 ③ 得: 得: 拓展练习小结适用于未知数的系数为1或-11、变形:将方程组里的一个方程变形,用含有一个未知数的一次式表示另一个未知数2、代入求解(把变形后的方程代入到另一个方程中,消元后求出未知数的值3、回代求解(把求得的未知数的值代入到变形的方程中,求出另一个未知数的值4、写解
