初中数学苏科版九下 “一动一定型”最值问题浅折 教学案(含答案)
文档属性
| 名称 | 初中数学苏科版九下 “一动一定型”最值问题浅折 教学案(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 248.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-20 10:22:56 | ||
图片预览

文档简介
“一动一定型”最值问题浅折
最值问题是近几年各地中考的热点,也是许多学生感觉比较棘手的问题.实际上,仔细分析,解决此类问题仍有规律可循,就线段的最大或最小而言,不外两种情形:(1)一动一定;(2)两动.解题的方法就是:分析动点的特征,怎么动,在哪里动 下面举例分析.
例1
如图1,
、均是边长为的等边三角形,点是边、的中点,直线、相交于点.当绕点旋转时,线段长的最小值是(
)
A.
B.
C.
D.
分析
此题关键是证.分析知动点在为直径的圆上,故过圆心存
在最大或最小,为最大,为最小.
例2
如图2,、是正方形的边上两个动点,满足,连结交于点,连结交于点,若正方形的边长为,则线段长度的最小值是
.
分析
此题的核心是证.分析可知动点在为直径的圆上运动,故过圆心时存在最大或最小.
注
此题来源八年级(上),是几何常规题.
例3
已知,,,,连、,相交于点.
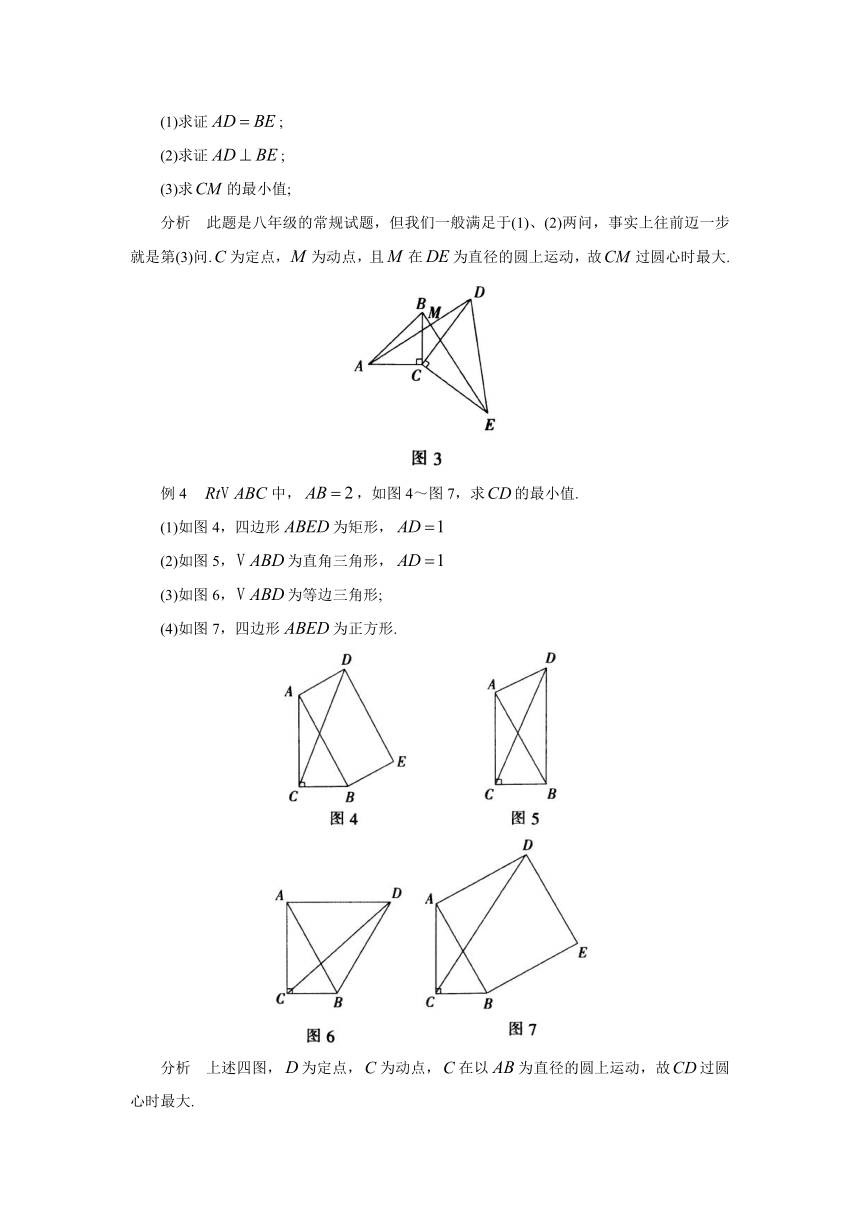
(1)求证;
(2)求证;
(3)求的最小值;
分析
此题是八年级的常规试题,但我们一般满足于(1)、(2)两问,事实上往前迈一步就是第(3)问.为定点,为动点,且在为直径的圆上运动,故过圆心时最大.
例4
中,,如图4~图7,求的最小值.
(1)如图4,四边形为矩形,
(2)如图5,为直角三角形,
(3)如图6,为等边三角形;
(4)如图7,四边形为正方形.
分析
上述四图,为定点,为动点,在以为直径的圆上运动,故过圆心时最大.
例5
如图8,边长为的菱形的两个顶点、别在轴,轴的正半轴上运动,、都在第一象限,,则的长的最大值是
.
方法1
取的中点,连,,,则
当、、共线时,最大,最大值为.
方法2
过、、三点作圆⊙,当过圆心时,最大.
注
此题是上题的变式.
例6如图9,中,,,,,点在射线上运动,连交的外接圆于点,则的最小值为(
)
A.
B.
C.
D.
分析
易知,,故为定点,为动点,在为弦长,为圆周角的圆上运动,过圆心时存在最大或最小.
在下方作等腰,,连,,以为圆心,为半径作⊙,连,最小值为(图形略),故选.
例7
如图10,在等边中,,、为、上两动点,,、相交于点,求的最小值.
分析
易证.又为定点,为动点,在以为弦长,圆周角为的圆上运动,故过圆心时存在最小.
上述数例都为同一个题型,看似不同,实际本质相同.我们要学会从中寻找一般性的规律,从而做到会一题,通一类.
最值问题是近几年各地中考的热点,也是许多学生感觉比较棘手的问题.实际上,仔细分析,解决此类问题仍有规律可循,就线段的最大或最小而言,不外两种情形:(1)一动一定;(2)两动.解题的方法就是:分析动点的特征,怎么动,在哪里动 下面举例分析.
例1
如图1,
、均是边长为的等边三角形,点是边、的中点,直线、相交于点.当绕点旋转时,线段长的最小值是(
)
A.
B.
C.
D.
分析
此题关键是证.分析知动点在为直径的圆上,故过圆心存
在最大或最小,为最大,为最小.
例2
如图2,、是正方形的边上两个动点,满足,连结交于点,连结交于点,若正方形的边长为,则线段长度的最小值是
.
分析
此题的核心是证.分析可知动点在为直径的圆上运动,故过圆心时存在最大或最小.
注
此题来源八年级(上),是几何常规题.
例3
已知,,,,连、,相交于点.
(1)求证;
(2)求证;
(3)求的最小值;
分析
此题是八年级的常规试题,但我们一般满足于(1)、(2)两问,事实上往前迈一步就是第(3)问.为定点,为动点,且在为直径的圆上运动,故过圆心时最大.
例4
中,,如图4~图7,求的最小值.
(1)如图4,四边形为矩形,
(2)如图5,为直角三角形,
(3)如图6,为等边三角形;
(4)如图7,四边形为正方形.
分析
上述四图,为定点,为动点,在以为直径的圆上运动,故过圆心时最大.
例5
如图8,边长为的菱形的两个顶点、别在轴,轴的正半轴上运动,、都在第一象限,,则的长的最大值是
.
方法1
取的中点,连,,,则
当、、共线时,最大,最大值为.
方法2
过、、三点作圆⊙,当过圆心时,最大.
注
此题是上题的变式.
例6如图9,中,,,,,点在射线上运动,连交的外接圆于点,则的最小值为(
)
A.
B.
C.
D.
分析
易知,,故为定点,为动点,在为弦长,为圆周角的圆上运动,过圆心时存在最大或最小.
在下方作等腰,,连,,以为圆心,为半径作⊙,连,最小值为(图形略),故选.
例7
如图10,在等边中,,、为、上两动点,,、相交于点,求的最小值.
分析
易证.又为定点,为动点,在以为弦长,圆周角为的圆上运动,故过圆心时存在最小.
上述数例都为同一个题型,看似不同,实际本质相同.我们要学会从中寻找一般性的规律,从而做到会一题,通一类.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
