7.1.2 平面直角坐标系(第2课时)课件
文档属性
| 名称 | 7.1.2 平面直角坐标系(第2课时)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 458.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-26 00:00:00 | ||
图片预览


文档简介
课件14张PPT。7.1.2 平面直角坐标系
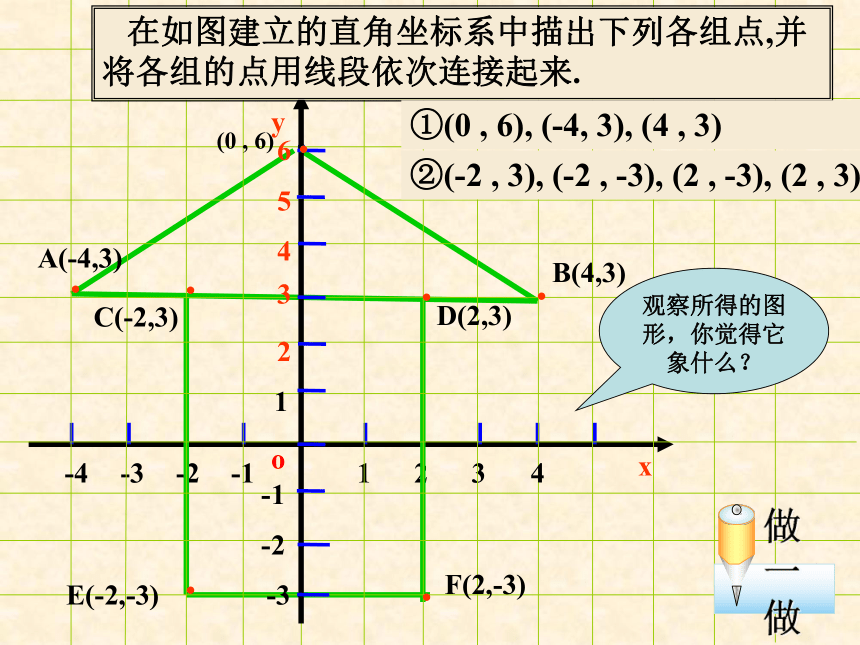
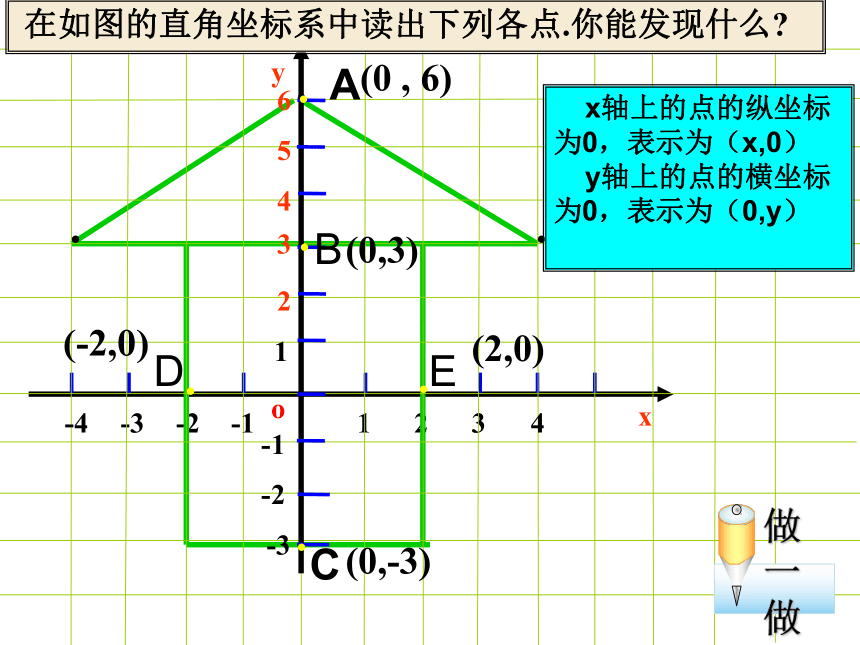
(第2课时)·-2-3o-11 在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.①(0 , 6), (-4, 3), (4 , 3) ②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)······观察所得的图形,你觉得它象什么?-4-14A(-4,3)B(4,3)C(-2,3)D(2,3)E(-2,-3)F(2,-3)(0 , 6)··-2-3o-11 在如图的直角坐标系中读出下列各点.你能发现什么?······-4-14(0 , 6)·ABC(0,-3)(0,3)DE(-2,0)(2,0) x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
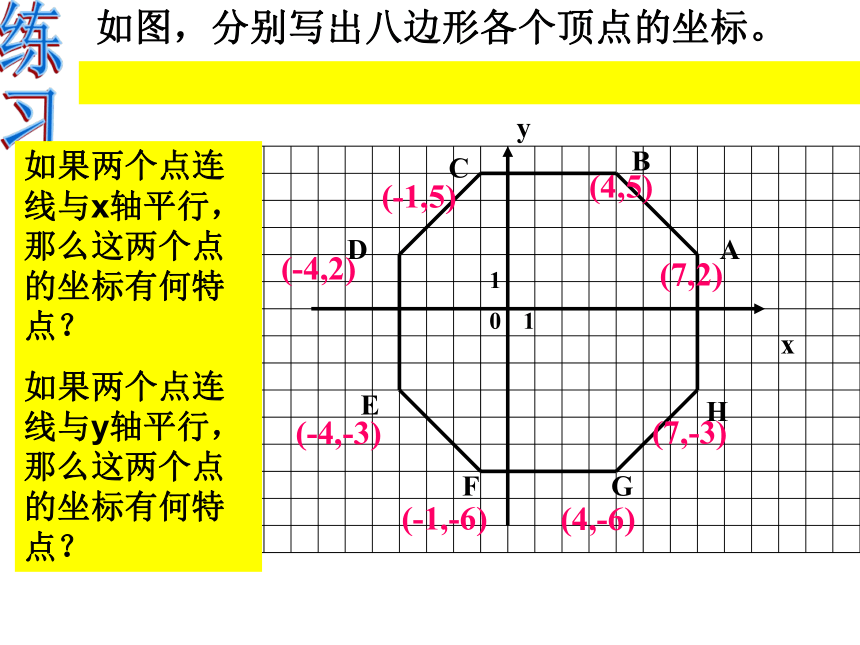
如图,分别写出八边形各个顶点的坐标。练习(7,2)(4,5)(-1,5)(-4,2)(-4,-3)(-1,-6)(4,-6)(7,-3)如果两个点连线与x轴平行,那么这两个点的坐标有何特点?
如果两个点连线与y轴平行,那么这两个点的坐标有何特点?结论纵坐标相同的点的连线平行于x轴横坐标相同的点的连线平行于y轴坐标轴的点至少有一个是0
x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
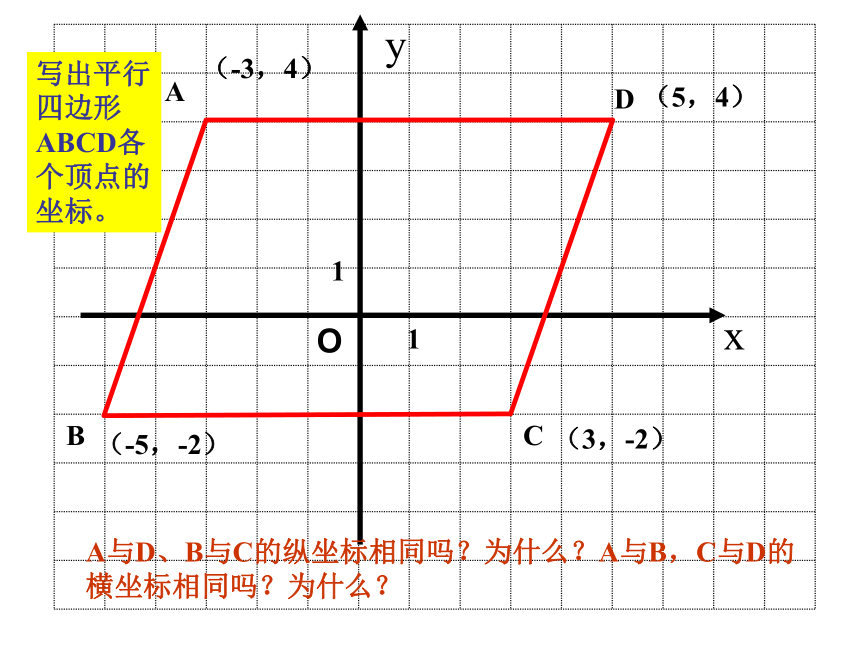
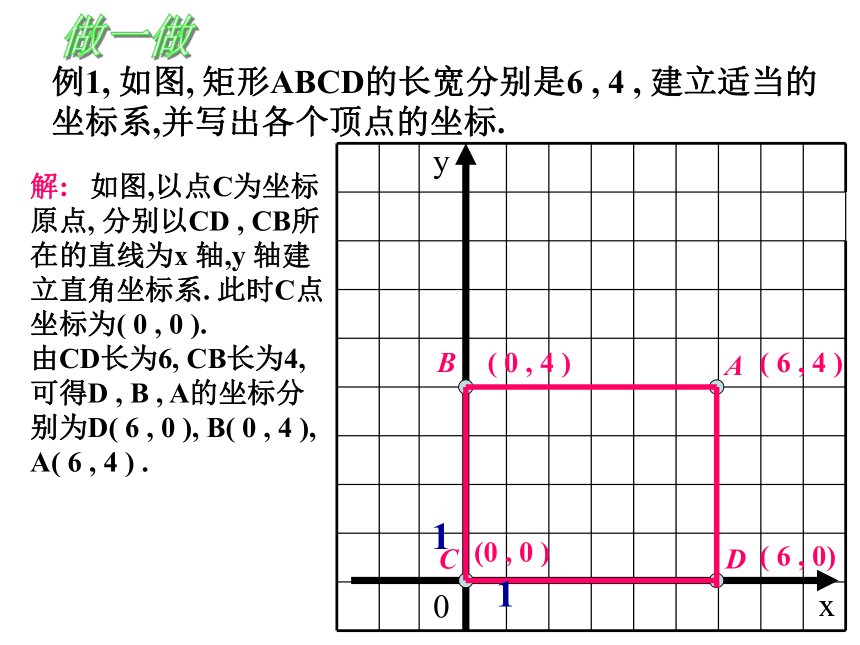
11(-3,4)(-5,-2)(3,-2)(5,4)A与D、B与C的纵坐标相同吗?为什么?A与B,C与D的横坐标相同吗?为什么?xy写出平行四边形ABCD各个顶点的坐标。例1, 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标. BCDA解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
做一做xy0(0 , 0 )( 0 , 4 )( 6 , 4 )( 6 , 0)11例1, 如图, 矩形ABCD的长宽分别是6 , 4 ,
建立适当的坐标系,并写出各个顶点的坐标. BCDA解: 如图,分别以两对边
中点的连线为x 轴,y 轴
建立直角坐标系. 此时
各顶点坐标为A( 3 , 2),
B( -3 , 2 ),C( -3 , -2 ), D( 3 , -2 ) .
做一做xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数议一议123·OXP(3,2)·B(3,-2)A(-3,2)C(-3,- 2 ) ··你能说出点P关于x轴、y轴、原点的对称点坐标吗?·★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )a,-b- a, b-a,-b练习根据实际情况建立适当的坐标系
如图,正方形ABCD的边长为6,
1、若以点A为原点,AB所在的直线
为x轴,建立平面直角坐标系,则y轴
的位置在线段______上,正方形的顶点A,B,C,D的坐标
分别为:A( ),B( ),C( ),D( ).AD0,06,06,60,62、若以线段DC所在的直线为x轴,纵轴
(y轴)位置不变,则四个顶点的坐标分别为:
A( ),B( ),C( ),
D( ).0,-66,-66,00,0yy4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对2.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。4.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置1.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限Ba<0b>1B3.点A(1-a,5),B(3 ,b)关于y轴对称,
则a=___,b=____。
45巩固练习:在一次“寻宝”游戏中,寻宝人已经找到了坐标为
(3,2)和(3,-2)的两个标志点,并且知道藏宝
地点的坐标为(4,4),除此之外不知道其他信息,
如何确定直角坐标系找到“宝藏”?请跟同伴交流。·123·O(3,-2)X(3,2)··(4,4)考考你告诉大家
本节课你的学会了什么!
y轴上的点的横坐标为0,表示为(0,y)
如图,分别写出八边形各个顶点的坐标。练习(7,2)(4,5)(-1,5)(-4,2)(-4,-3)(-1,-6)(4,-6)(7,-3)如果两个点连线与x轴平行,那么这两个点的坐标有何特点?
如果两个点连线与y轴平行,那么这两个点的坐标有何特点?结论纵坐标相同的点的连线平行于x轴横坐标相同的点的连线平行于y轴坐标轴的点至少有一个是0
x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
11(-3,4)(-5,-2)(3,-2)(5,4)A与D、B与C的纵坐标相同吗?为什么?A与B,C与D的横坐标相同吗?为什么?xy写出平行四边形ABCD各个顶点的坐标。例1, 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的
坐标系,并写出各个顶点的坐标. BCDA解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
做一做xy0(0 , 0 )( 0 , 4 )( 6 , 4 )( 6 , 0)11例1, 如图, 矩形ABCD的长宽分别是6 , 4 ,
建立适当的坐标系,并写出各个顶点的坐标. BCDA解: 如图,分别以两对边
中点的连线为x 轴,y 轴
建立直角坐标系. 此时
各顶点坐标为A( 3 , 2),
B( -3 , 2 ),C( -3 , -2 ), D( 3 , -2 ) .
做一做xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数议一议123·OXP(3,2)·B(3,-2)A(-3,2)C(-3,- 2 ) ··你能说出点P关于x轴、y轴、原点的对称点坐标吗?·★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )a,-b- a, b-a,-b练习根据实际情况建立适当的坐标系
如图,正方形ABCD的边长为6,
1、若以点A为原点,AB所在的直线
为x轴,建立平面直角坐标系,则y轴
的位置在线段______上,正方形的顶点A,B,C,D的坐标
分别为:A( ),B( ),C( ),D( ).AD0,06,06,60,62、若以线段DC所在的直线为x轴,纵轴
(y轴)位置不变,则四个顶点的坐标分别为:
A( ),B( ),C( ),
D( ).0,-66,-66,00,0yy4.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对2.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。4.实数 x,y满足 (x-1)2+ |y| = 0,则点 P( x,y)在【 】. (A)原点 (B)x轴正半轴
(C)第一象限 (D)任意位置1.在平面直角坐标系内,已知点P ( a , b ), 且a b < 0 ,
则点P的位置在____________。
第二或四象限Ba<0b>1B3.点A(1-a,5),B(3 ,b)关于y轴对称,
则a=___,b=____。
45巩固练习:在一次“寻宝”游戏中,寻宝人已经找到了坐标为
(3,2)和(3,-2)的两个标志点,并且知道藏宝
地点的坐标为(4,4),除此之外不知道其他信息,
如何确定直角坐标系找到“宝藏”?请跟同伴交流。·123·O(3,-2)X(3,2)··(4,4)考考你告诉大家
本节课你的学会了什么!
