一次函数复习 课件
图片预览










文档简介
课件30张PPT。《一次函数》复习黄冈中学网校 林老师一、变量与函数一般的,在一个变化过程中,如果有两个x与y,并且对于x的每一个变化值,y都有唯一确定的值与其对应,那么就称y是x的函数,其中x是自变量,如果当x=a时,y=b,那么b叫做自变量的值为a时的函数。 《一次函数》复习7、在函数y= 中,当函数值y=1时,自变量x的值是 ;当自变量x=1时,函数y的值是 。自变量x取范围是 。2x≠-1《一次函数》复习二、函数图像(1)函数的表示方法: 、 、 。
(2)三种函数表示方法的优缺点:
① 法能明显地显示出自变量与其对应的函数值,但具有 性。
② 法形象直观,但画出的图象是近似的局部的,往往不够准确。
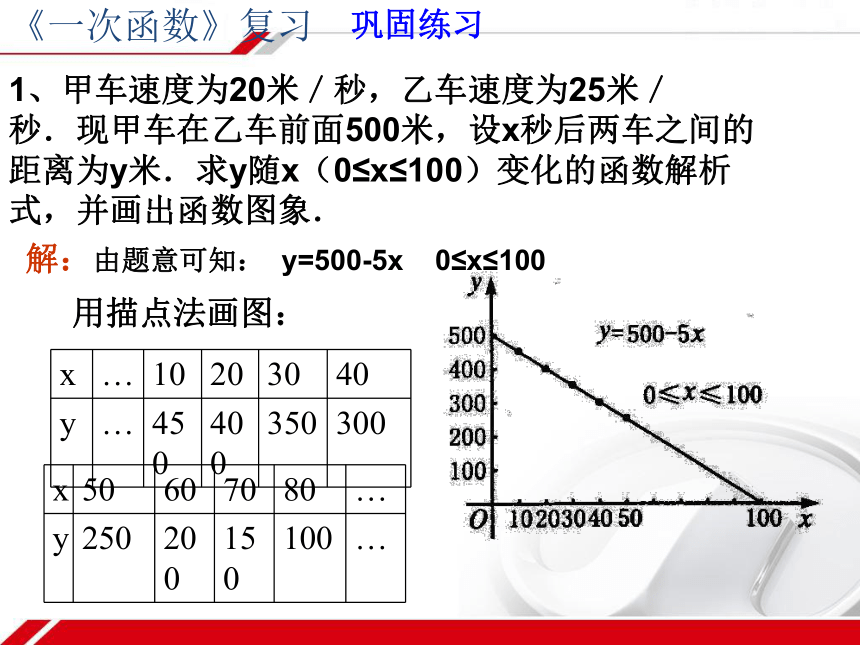
③ 法的优点是简单明了,但它在求对应值时,往往需要复杂的计算才能得出。解析式法图像法列表法列表片面图像法解析式《一次函数》复习巩固练习1、甲车速度为20米/秒,乙车速度为25米/秒.现甲车在乙车前面500米,设x秒后两车之间的距离为y米.求y随x(0≤x≤100)变化的函数解析式,并画出函数图象. 解:由题意可知: y=500-5x 0≤x≤100 用描点法画图: 《一次函数》复习三、正比例函数1、形如 (k是常数,k≠0)的函数,叫做正比例函数,其中k叫比例函数。
2、(1)正比例函数y=kx( k是常数,k≠0)的图象是一条经过 ,也称它为 ;
(2)画y=kx的图象时,一般选 点和______ 画 ,简称两点法。
3、(1)当k>0时,直线y=kx依次经过 象限,从 左向右 ,y随x的增大而 。
(2)当k<0时,直线y=kx依次经过第 象限。从 左向右 ,y随x的增大而 。y=kx原点的直线直线y=kx原直线一、三上升增大二、四下降减小(1,k)1、下列函数中,y是x的正比例函数的是( )《一次函数》复习巩固练习A、y=4x+1 B、y=2x2 C、y=- x D、y=C2、下列图象中,是正比例函数y=2x的图象的是( )3、已知正比例函数y=kx(k≠0),点(2,-3 )在该函数的图象上,则y随x的增大而 (增大或减小)B减小4、 正比例函数y=—x经过第________象限,图象从左到右呈_______趋势,y随着x的增大而______。
5、正比例函数y=kx的图象经过点A(3,6),写出这正比例函数的解析式______________。
6、请写出右图函数图像的解析式_____________,自变量的取值范围是_________。
二、四下降减小y=2xx≥07、根据下列条件求函数的解析式,函数
y=(k2-9)x2+(k+1)x是正比例函数,且y随x的增大而减小。解:由题意,得k2-9=0 ∴k=3或k=-3
∵y随x的增大而减小 ∴k+1<0 ∴k= -3
∴y与x的函数关系式是y= -2x8、y与x+2成正比例,且x= -1时,y=6,求y与x的关系式解:∵y与x成正比例 ∴设y=k(x+2)
∵x=-1,y=6 ∴6=k(-1+2)
∴k=6
∴函数的关系式为:y=6x+129、若函数y=(2m+6)x2+(1-m)x是正比例函数,则其解析式是 ,该图象经过 象限,y随x的增大而 ,当x1<x2时,则y1与y2的关是 。y=4x第一、三增大y1<y2解:∵函数y=(2m+6)x2+(1-m)x是正比例函数
∴2m+6=0,1-m≠0
∴m=-3
∴函数的解析式为:y=4x《一次函数》复习四、一次函数定义与性质一次函数的定义:一般地,形如 ,(k、b是常数,k≠0)的函数叫做一次函数,当 时,一次函数y=kx+b(k ≠0)也叫正比例函数。y=kx+bb=0一次函数的性质:①一次函数y=kx+b(k≠0)的图象是 ,称为 y=kx=b ;
②直线y=kx+b(k≠0)可以看做直y=kx(k≠0)平移 个单位长度而得到,当b>0时,向 平移;当b<0时,向 平移。
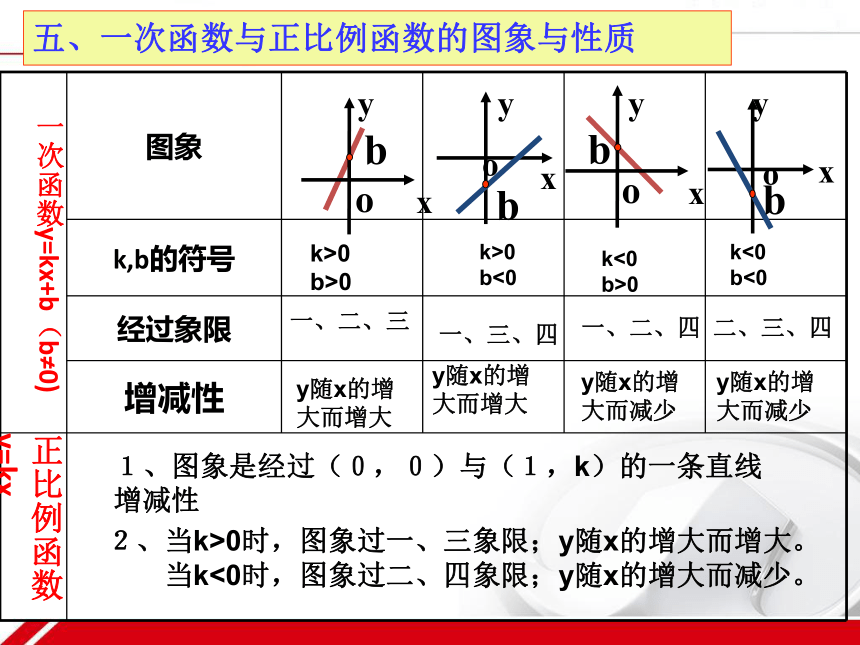
?如果两条直线互相平行,那么两一次函数的k值相同一条直线直线b上下五、一次函数与正比例函数的图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四1、图象是经过(0,0)与(1,k)的一条直线
增减性
2、当k>0时,图象过一、三象限;y随x的增大而增大。
当k<0时,图象过二、四象限;y随x的增大而减少。k>0
b>0k>0
b<0k<0
b>0k<0
b<06、根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号: k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___05、有下列函数:①y=2x+1, ②y=-3x+4,③y=0.5x,④y=x-6; ① ④②③①函数y随x的增大而增大的是__________;其中过原点的直线是________;函数y随x的增大而减小的是___________;图象在第一、二、三象限的是________ 。1、当k________时,y=(k—3)x—5是一次函数。
2、对于函数y=5x+6,y的值随x值的减小而___________。
3、一次函数y=-2x+4的图象经过的第___________象限,它与x轴的交点坐标是( , ),与y轴的交点坐标是( , )。
4、已知直线y=x+6与x轴,y轴围成一个三角形面积为___________。≠3减小一、二、四2 00 418《一次函数》复习巩固练习5、直线y=4x向_______平移______个单位得到直线y=4x+2。上2解析:函数y=kx平行情况
(1)将函数向上平行b个单位,函数为y=kx+b
将函数向下平行b个单位,函数为y=kx-b6、两直线y=3x与y=kx+2平行,则k=_____。3解析:两直线平行,k值相同8、已知一次函y=(m-1)x+(2-m)
(1)当m_______时,y随x的增大而减小。
(2)当m_______时,函数的图象过原点。 ﹤1=27、两直线y=-4x+6与y=3x+6相交于点( , )0 6解析:一次函数中求两直线的交点,既是将两一次函数联立成二元一次方程组,求出x和y。解析:(1)一次函数中,当k<0时,y随x的增大而减下,所以m-1<0,得m<1
(2)当b=0时,一次函数为正比例函数,图像经过原点,所以2-m=0,得m=29、若函数y=kx+b的图象平等于直线y=-2x,且与y轴交于点(0,3),则k= ,b= 。-2310、已知一次函数y=(3m-8)x+1-m图象与y轴交点在x轴下方,且y随x的增大而减小,其中m为整数。
(1)求m的值;(2)当x取何值时,0(2)当m=2时,y=-2x-1又由于05=1×k
K=5
所以这正比例函数的解析式是y=5x。
《一次函数》复习 巩固练习2、已知一次函数的图象经过点(2,1)和(-1,-2),求此一次函数的解析式 。若它的图象经过点(5,m),求m的值。3.已知一次函数y=kx+b的图象经过点(3,- 1),且与直线y=4x-3的交点在Y轴上.
(1).求这个函数的解析式
(2).此一次函数的图象经过哪几个象限?
(3).求此函数的图象与坐标轴围成的三角形的面积?4.(2012?中考题)已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.《一次函数》复习七、函数与方程(组)、不等式1.填空:(1)方程2x+20=0的解是 ;当函数y=2x+20的函数值为
0,x= 。X= -10-10(2).观察函数y=2x+20的图象可知:函数y=2x+20与x轴的交点坐标是 ,即方程2x+20=0的解是 。归纳:从“数”上看:求方程ax+b=0(a,b是常数,a≠0)的解,就是当x为何值时,函数y=ax+b的值为0;从“形”上看:求方程ax+b=0(a,b是常数,a≠0)的解,就是求直线y=ax+b与x轴交点的坐标(- 10,0)X= -10(1).不等式2x+20>0的解集 ;当函数y=2x+20的函数值大于0时,x的取值范围是 。
(2).函数y=2x+20在x轴上方的图象所对应的自变量x的取值范围是 ;即不等式2x+20>0的解集是 。
(3).函数y=2x+20在x轴下方的图象所对应的自变量x的取值范围是 ;即不等式2x+20<0的解是 。X >-10X >-10X >-10X >-10X <-10X <-10归纳:解关于x的不等式kx+b>0或kx+b<0的
转化思想:
(1).kx+b>0转化为直线y=kx+b在x轴
的 方的点所对应的 的取值;
(2). kx+b<0转化为直线y=kx+b在x轴
的 方的点所对应的 的取值;上x下x1、直线y=-2x+4与x轴交点的坐标为(2,0),所以相应方程 的解为_____________。
2、若直线y=3x+4和直线y=-2x-6交于点A,则点A的坐标是______。
3、一次函数图象如右图,当x<3时y的取值范围是_____。 x=2(-2,-2)y>0《一次函数》复习 巩固练习4.如图,直线y=kx+b与x轴交与点(1,0)与y轴交于点(0,- 2),则kx+b=0 的根为( )
A.x= - 2 B.x=0 C. x=1 D.X=1C5、已知一次函数y=kx+3的图象如图所示,则不等式kx+3<0的解集是 . X>1.56、一次函数y=kx +b(k,b为常数,且k≠0)的图象如图所示。根据图象信息可求得关于x的方程kx+b=3的解为 .X=27.如图直线y=kx+b分别交x轴、y轴于点A、B,回答下列问题:
(1).关于x的方程的kx+b=0的解是什么?
(2).当x为何值时,0<y<3?
(3) . 求x为何值时,y>1?解 : (1).由图象可知直线与x轴的交点A(- 2,0), ∴kx+b=0解为x=-2.
(2).由图象可知当 -2<x<0时,0<y<3.
(3)由图像可知一次函数交于点(-2,0),(0,3);
将两点代入y=kx+b中可得 解得:k=3/2, b=3, 直
线 , 当y>1,则3/2x+3>1,∴ .1、写出一个经过(-1,4)的函数解析式__________________。
2、写出下列函数自变量x的取值范围
y= x(x+3)____________ ; ____________
____________; ____________
3、已知一次函数 +3,则k=_________。
4、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第___________象限。
5、直线y=4x+2向_______平移______个单位得到直线y=4x。
6、方程-2x+4=0的解为_______ ,所以直线y=-2x+4与x轴交点的坐标为_______ 。
7、无论m为何值,直线y=x+2m与直线y=-x+4的交点不可能在第______象限。y=-4x (答案不唯一)X取任意实数X≥0.5X≠ -2- 1二、三、四下2X=2(2,0)三《一次函数》复习 八、小组讨论 一 次 函 数正 比 例 函 数解析式 图 象性 质应 用 y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0) k>0 k<0 k>0 k<0 k>0,b>0k>0,b<0k<0,b>0k<0,b<0yxoxyok>0时,在一, 三象限;
k<0时,在二, 四象限.
正比例函数是特殊的一次函数k>0,b>0时在一, 二,三象限;
k>0,b<0时在一, 三, 四 象限
k<0, b>0时,在一,二, 四象限.
k<0, b<0时,在二, 三, 四象限
平行于 y = k x ,可由它平移而得当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小. 一 次 函 数正 比 例 函 数解析式 图 象性 质应 用 y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0) k>0 k<0 k>0 k<0 k>0,b>0k>0,b<0k<0,b>0k<0,b<0yxoxyok>0时,在一, 三象限;
k<0时,在二, 四象限.
正比例函数是特殊的一次函数k>0,b>0时在一, 二,三象限;
k>0,b<0时在一, 三, 四 象限
k<0, b>0时,在一,二, 四象限.
k<0, b<0时,在二, 三, 四象限
平行于 y = k x ,可由它平移而得当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
(2)三种函数表示方法的优缺点:
① 法能明显地显示出自变量与其对应的函数值,但具有 性。
② 法形象直观,但画出的图象是近似的局部的,往往不够准确。
③ 法的优点是简单明了,但它在求对应值时,往往需要复杂的计算才能得出。解析式法图像法列表法列表片面图像法解析式《一次函数》复习巩固练习1、甲车速度为20米/秒,乙车速度为25米/秒.现甲车在乙车前面500米,设x秒后两车之间的距离为y米.求y随x(0≤x≤100)变化的函数解析式,并画出函数图象. 解:由题意可知: y=500-5x 0≤x≤100 用描点法画图: 《一次函数》复习三、正比例函数1、形如 (k是常数,k≠0)的函数,叫做正比例函数,其中k叫比例函数。
2、(1)正比例函数y=kx( k是常数,k≠0)的图象是一条经过 ,也称它为 ;
(2)画y=kx的图象时,一般选 点和______ 画 ,简称两点法。
3、(1)当k>0时,直线y=kx依次经过 象限,从 左向右 ,y随x的增大而 。
(2)当k<0时,直线y=kx依次经过第 象限。从 左向右 ,y随x的增大而 。y=kx原点的直线直线y=kx原直线一、三上升增大二、四下降减小(1,k)1、下列函数中,y是x的正比例函数的是( )《一次函数》复习巩固练习A、y=4x+1 B、y=2x2 C、y=- x D、y=C2、下列图象中,是正比例函数y=2x的图象的是( )3、已知正比例函数y=kx(k≠0),点(2,-3 )在该函数的图象上,则y随x的增大而 (增大或减小)B减小4、 正比例函数y=—x经过第________象限,图象从左到右呈_______趋势,y随着x的增大而______。
5、正比例函数y=kx的图象经过点A(3,6),写出这正比例函数的解析式______________。
6、请写出右图函数图像的解析式_____________,自变量的取值范围是_________。
二、四下降减小y=2xx≥07、根据下列条件求函数的解析式,函数
y=(k2-9)x2+(k+1)x是正比例函数,且y随x的增大而减小。解:由题意,得k2-9=0 ∴k=3或k=-3
∵y随x的增大而减小 ∴k+1<0 ∴k= -3
∴y与x的函数关系式是y= -2x8、y与x+2成正比例,且x= -1时,y=6,求y与x的关系式解:∵y与x成正比例 ∴设y=k(x+2)
∵x=-1,y=6 ∴6=k(-1+2)
∴k=6
∴函数的关系式为:y=6x+129、若函数y=(2m+6)x2+(1-m)x是正比例函数,则其解析式是 ,该图象经过 象限,y随x的增大而 ,当x1<x2时,则y1与y2的关是 。y=4x第一、三增大y1<y2解:∵函数y=(2m+6)x2+(1-m)x是正比例函数
∴2m+6=0,1-m≠0
∴m=-3
∴函数的解析式为:y=4x《一次函数》复习四、一次函数定义与性质一次函数的定义:一般地,形如 ,(k、b是常数,k≠0)的函数叫做一次函数,当 时,一次函数y=kx+b(k ≠0)也叫正比例函数。y=kx+bb=0一次函数的性质:①一次函数y=kx+b(k≠0)的图象是 ,称为 y=kx=b ;
②直线y=kx+b(k≠0)可以看做直y=kx(k≠0)平移 个单位长度而得到,当b>0时,向 平移;当b<0时,向 平移。
?如果两条直线互相平行,那么两一次函数的k值相同一条直线直线b上下五、一次函数与正比例函数的图象与性质y随x的增
大而增大y随x的增
大而增大y随x的增
大而减少y随x的增
大而减少一、二、三一、三、四一、二、四二、三、四1、图象是经过(0,0)与(1,k)的一条直线
增减性
2、当k>0时,图象过一、三象限;y随x的增大而增大。
当k<0时,图象过二、四象限;y随x的增大而减少。k>0
b>0k>0
b<0k<0
b>0k<0
b<06、根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号: k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___05、有下列函数:①y=2x+1, ②y=-3x+4,③y=0.5x,④y=x-6; ① ④②③①函数y随x的增大而增大的是__________;其中过原点的直线是________;函数y随x的增大而减小的是___________;图象在第一、二、三象限的是________ 。1、当k________时,y=(k—3)x—5是一次函数。
2、对于函数y=5x+6,y的值随x值的减小而___________。
3、一次函数y=-2x+4的图象经过的第___________象限,它与x轴的交点坐标是( , ),与y轴的交点坐标是( , )。
4、已知直线y=x+6与x轴,y轴围成一个三角形面积为___________。≠3减小一、二、四2 00 418《一次函数》复习巩固练习5、直线y=4x向_______平移______个单位得到直线y=4x+2。上2解析:函数y=kx平行情况
(1)将函数向上平行b个单位,函数为y=kx+b
将函数向下平行b个单位,函数为y=kx-b6、两直线y=3x与y=kx+2平行,则k=_____。3解析:两直线平行,k值相同8、已知一次函y=(m-1)x+(2-m)
(1)当m_______时,y随x的增大而减小。
(2)当m_______时,函数的图象过原点。 ﹤1=27、两直线y=-4x+6与y=3x+6相交于点( , )0 6解析:一次函数中求两直线的交点,既是将两一次函数联立成二元一次方程组,求出x和y。解析:(1)一次函数中,当k<0时,y随x的增大而减下,所以m-1<0,得m<1
(2)当b=0时,一次函数为正比例函数,图像经过原点,所以2-m=0,得m=29、若函数y=kx+b的图象平等于直线y=-2x,且与y轴交于点(0,3),则k= ,b= 。-2310、已知一次函数y=(3m-8)x+1-m图象与y轴交点在x轴下方,且y随x的增大而减小,其中m为整数。
(1)求m的值;(2)当x取何值时,0
K=5
所以这正比例函数的解析式是y=5x。
《一次函数》复习 巩固练习2、已知一次函数的图象经过点(2,1)和(-1,-2),求此一次函数的解析式 。若它的图象经过点(5,m),求m的值。3.已知一次函数y=kx+b的图象经过点(3,- 1),且与直线y=4x-3的交点在Y轴上.
(1).求这个函数的解析式
(2).此一次函数的图象经过哪几个象限?
(3).求此函数的图象与坐标轴围成的三角形的面积?4.(2012?中考题)已知一次函数y=kx+b(k≠0)图象过点(0,2),且与两坐标轴围成的三角形面积为2,求此一次函数的解析式.《一次函数》复习七、函数与方程(组)、不等式1.填空:(1)方程2x+20=0的解是 ;当函数y=2x+20的函数值为
0,x= 。X= -10-10(2).观察函数y=2x+20的图象可知:函数y=2x+20与x轴的交点坐标是 ,即方程2x+20=0的解是 。归纳:从“数”上看:求方程ax+b=0(a,b是常数,a≠0)的解,就是当x为何值时,函数y=ax+b的值为0;从“形”上看:求方程ax+b=0(a,b是常数,a≠0)的解,就是求直线y=ax+b与x轴交点的坐标(- 10,0)X= -10(1).不等式2x+20>0的解集 ;当函数y=2x+20的函数值大于0时,x的取值范围是 。
(2).函数y=2x+20在x轴上方的图象所对应的自变量x的取值范围是 ;即不等式2x+20>0的解集是 。
(3).函数y=2x+20在x轴下方的图象所对应的自变量x的取值范围是 ;即不等式2x+20<0的解是 。X >-10X >-10X >-10X >-10X <-10X <-10归纳:解关于x的不等式kx+b>0或kx+b<0的
转化思想:
(1).kx+b>0转化为直线y=kx+b在x轴
的 方的点所对应的 的取值;
(2). kx+b<0转化为直线y=kx+b在x轴
的 方的点所对应的 的取值;上x下x1、直线y=-2x+4与x轴交点的坐标为(2,0),所以相应方程 的解为_____________。
2、若直线y=3x+4和直线y=-2x-6交于点A,则点A的坐标是______。
3、一次函数图象如右图,当x<3时y的取值范围是_____。 x=2(-2,-2)y>0《一次函数》复习 巩固练习4.如图,直线y=kx+b与x轴交与点(1,0)与y轴交于点(0,- 2),则kx+b=0 的根为( )
A.x= - 2 B.x=0 C. x=1 D.X=1C5、已知一次函数y=kx+3的图象如图所示,则不等式kx+3<0的解集是 . X>1.56、一次函数y=kx +b(k,b为常数,且k≠0)的图象如图所示。根据图象信息可求得关于x的方程kx+b=3的解为 .X=27.如图直线y=kx+b分别交x轴、y轴于点A、B,回答下列问题:
(1).关于x的方程的kx+b=0的解是什么?
(2).当x为何值时,0<y<3?
(3) . 求x为何值时,y>1?解 : (1).由图象可知直线与x轴的交点A(- 2,0), ∴kx+b=0解为x=-2.
(2).由图象可知当 -2<x<0时,0<y<3.
(3)由图像可知一次函数交于点(-2,0),(0,3);
将两点代入y=kx+b中可得 解得:k=3/2, b=3, 直
线 , 当y>1,则3/2x+3>1,∴ .1、写出一个经过(-1,4)的函数解析式__________________。
2、写出下列函数自变量x的取值范围
y= x(x+3)____________ ; ____________
____________; ____________
3、已知一次函数 +3,则k=_________。
4、已知直线y=kx+b经过第一、二、四象限,那么直线y=-bx+k经过第___________象限。
5、直线y=4x+2向_______平移______个单位得到直线y=4x。
6、方程-2x+4=0的解为_______ ,所以直线y=-2x+4与x轴交点的坐标为_______ 。
7、无论m为何值,直线y=x+2m与直线y=-x+4的交点不可能在第______象限。y=-4x (答案不唯一)X取任意实数X≥0.5X≠ -2- 1二、三、四下2X=2(2,0)三《一次函数》复习 八、小组讨论 一 次 函 数正 比 例 函 数解析式 图 象性 质应 用 y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0) k>0 k<0 k>0 k<0 k>0,b>0k>0,b<0k<0,b>0k<0,b<0yxoxyok>0时,在一, 三象限;
k<0时,在二, 四象限.
正比例函数是特殊的一次函数k>0,b>0时在一, 二,三象限;
k>0,b<0时在一, 三, 四 象限
k<0, b>0时,在一,二, 四象限.
k<0, b<0时,在二, 三, 四象限
平行于 y = k x ,可由它平移而得当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小. 一 次 函 数正 比 例 函 数解析式 图 象性 质应 用 y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0) k>0 k<0 k>0 k<0 k>0,b>0k>0,b<0k<0,b>0k<0,b<0yxoxyok>0时,在一, 三象限;
k<0时,在二, 四象限.
正比例函数是特殊的一次函数k>0,b>0时在一, 二,三象限;
k>0,b<0时在一, 三, 四 象限
k<0, b>0时,在一,二, 四象限.
k<0, b<0时,在二, 三, 四象限
平行于 y = k x ,可由它平移而得当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
