2016-2017高一物理沪科版必修2自我小测:4.1 势能的变化与机械功(含解析)
文档属性
| 名称 | 2016-2017高一物理沪科版必修2自我小测:4.1 势能的变化与机械功(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2017-04-25 16:00:22 | ||
图片预览

文档简介
自我小测
1如图所示,物体沿不同的路径从A运动到B,其中按不同的路径:①有摩擦作用;②无摩擦作用;③无摩擦,但有其他外力拉它。比较这三种情况下重力做的功W1、W2、W3,重力势能的变化量ΔEp1、ΔEp2、ΔEp3的关系,以下正确的是( )
A.W1>W2>W3
B.W1=W2=W3
C.ΔEp1=ΔEp2=ΔEp3
D.ΔEp1<ΔEp2<ΔEp3
2下列关于重力势能的说法中,错误的是( )
A.重力做正功,重力势能减少
B.重力做负功,重力势能增加
C.重力不做功,重力势能不变化
D.重力势能变化与重力做功无关
3用拉力F将一个重为5
N的物体匀速升高3
m,如图所示,在这个过程中,下列说法正确的是
…
( )
A.物体的重力做了15
J的功
B.拉力F对物体做了15
J的功
C.物体的重力势能增加了15
J
D.合力对物体做的功是15
J
4关于重力做功和重力势能变化,下列叙述正确的是( )
A.做竖直上抛运动的物体,在上升阶段,重力做负功,重力势能减少
B.做竖直上抛运动的物体,重力势能在不断减少
C.做平抛运动的物体,重力势能在不断减少
D.做匀速直线运动的物体,重力势能在不断减小
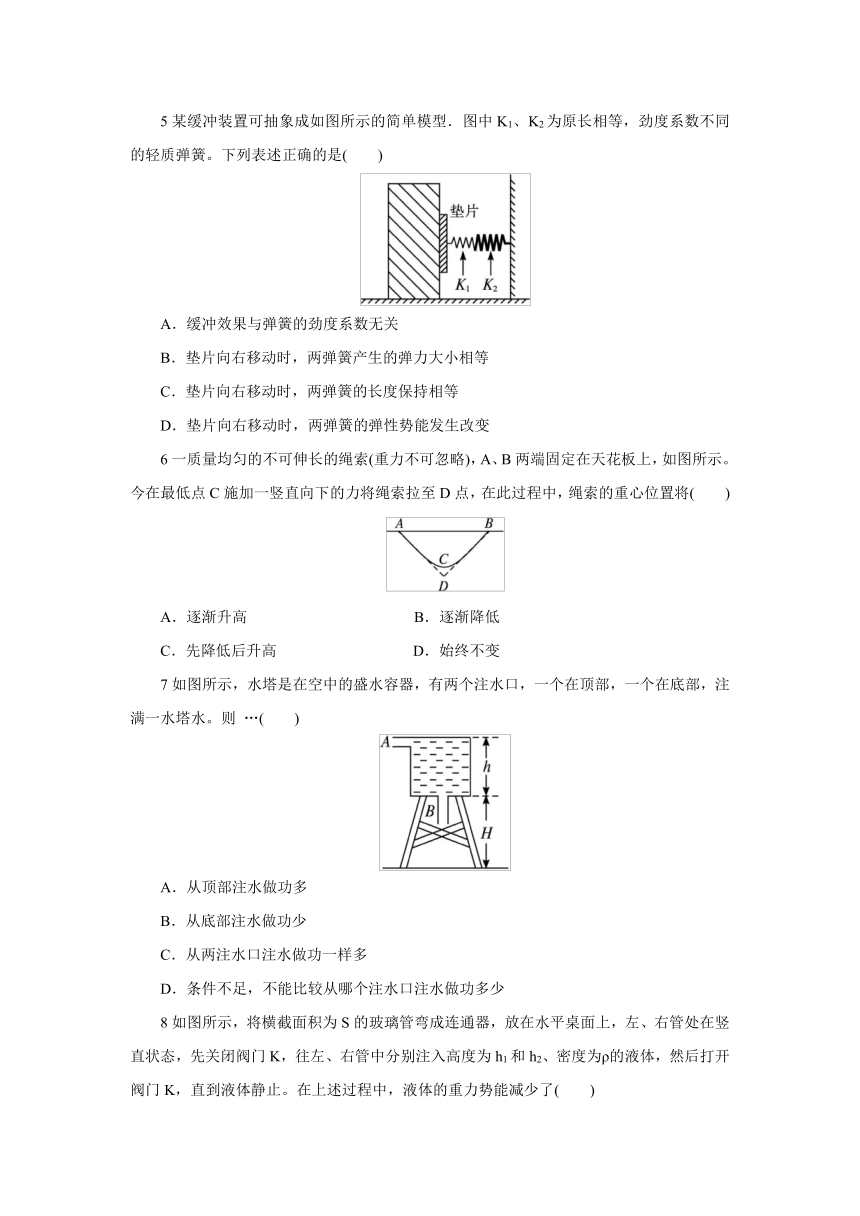
5某缓冲装置可抽象成如图所示的简单模型.图中K1、K2为原长相等,劲度系数不同的轻质弹簧。下列表述正确的是( )
A.缓冲效果与弹簧的劲度系数无关
B.垫片向右移动时,两弹簧产生的弹力大小相等
C.垫片向右移动时,两弹簧的长度保持相等
D.垫片向右移动时,两弹簧的弹性势能发生改变
6一质量均匀的不可伸长的绳索(重力不可忽略),A、B两端固定在天花板上,如图所示。今在最低点C施加一竖直向下的力将绳索拉至D点,在此过程中,绳索的重心位置将( )
A.逐渐升高
B.逐渐降低
C.先降低后升高
D.始终不变
7如图所示,水塔是在空中的盛水容器,有两个注水口,一个在顶部,一个在底部,注满一水塔水。则
…( )
A.从顶部注水做功多
B.从底部注水做功少
C.从两注水口注水做功一样多
D.条件不足,不能比较从哪个注水口注水做功多少
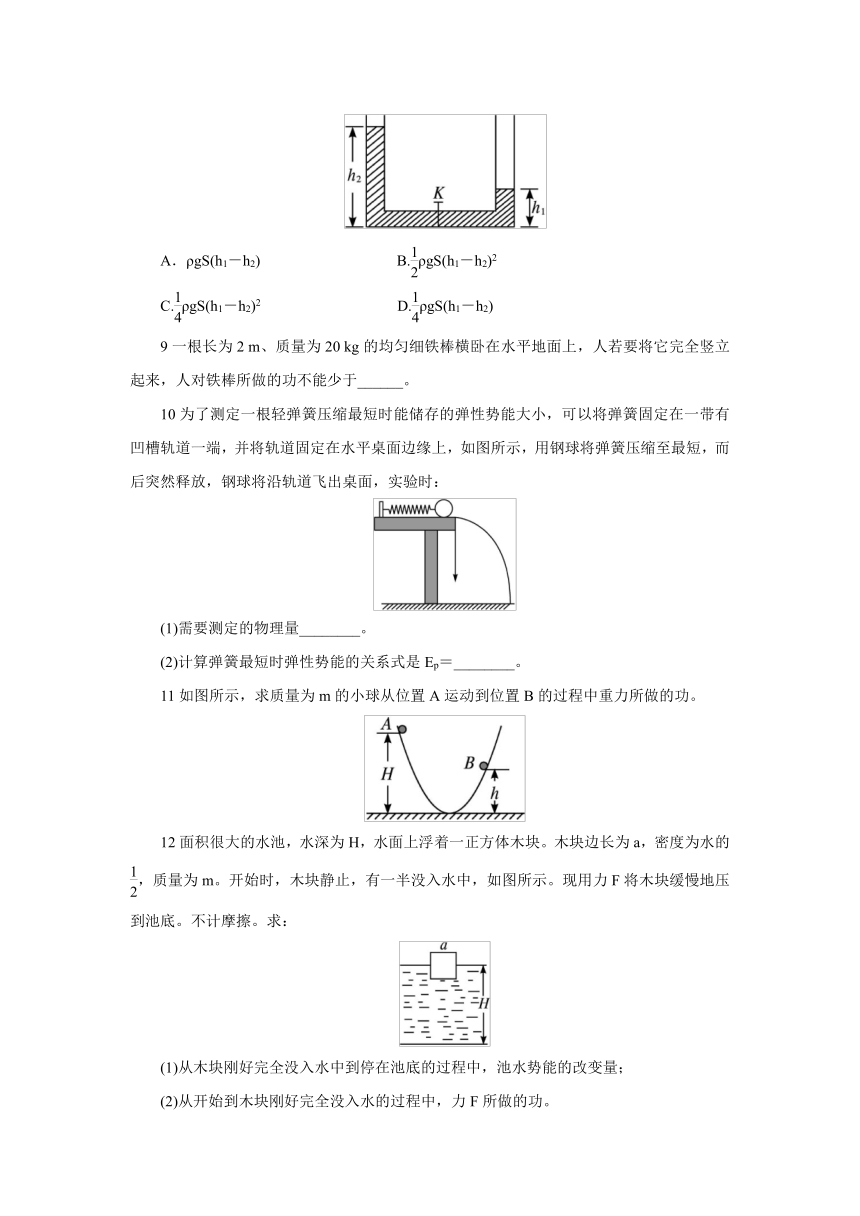
8如图所示,将横截面积为S的玻璃管弯成连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h1和h2、密度为ρ的液体,然后打开阀门K,直到液体静止。在上述过程中,液体的重力势能减少了( )
A.ρgS(h1-h2)
B.ρgS(h1-h2)2
C.ρgS(h1-h2)2
D.ρgS(h1-h2)
9一根长为2
m、质量为20
kg的均匀细铁棒横卧在水平地面上,人若要将它完全竖立起来,人对铁棒所做的功不能少于______。
10为了测定一根轻弹簧压缩最短时能储存的弹性势能大小,可以将弹簧固定在一带有凹槽轨道一端,并将轨道固定在水平桌面边缘上,如图所示,用钢球将弹簧压缩至最短,而后突然释放,钢球将沿轨道飞出桌面,实验时:
(1)需要测定的物理量________。
(2)计算弹簧最短时弹性势能的关系式是Ep=________。
11如图所示,求质量为m的小球从位置A运动到位置B的过程中重力所做的功。
12面积很大的水池,水深为H,水面上浮着一正方体木块。木块边长为a,密度为水的,质量为m。开始时,木块静止,有一半没入水中,如图所示。现用力F将木块缓慢地压到池底。不计摩擦。求:
(1)从木块刚好完全没入水中到停在池底的过程中,池水势能的改变量;
(2)从开始到木块刚好完全没入水的过程中,力F所做的功。
参考答案
1解析:重力做功与路径无关,取决于物体初、末位置,且与受不受其他力无关。重力势能的变化量只取决于重力做的功,因此,三种情况下重力做功相同,重力势能的变化量也相同。
答案:BC
2解析:重力势能变化取决于重力的做功情况。重力对物体做正功时,重力势能减小,物体克服重力做功,即重力做负功时,重力势能增加,且重力势能的变化量应等于重力所做功的负值,所以选项D错误。
答案:D
3解析:物体上升,重力做负功,WG=-mgh=-5×3
J=-15
J,选项A错误;因为物体匀速上升,所以拉力F=G=5
N,则拉力做功WF=Fh=5×3
J=15
J,选项B正确;因物体克服重力做功15
J,故物体重力势能增加15
J,选项C正确;因为物体匀速上升,合力为零,则合力不做功,选项D错误。
答案:BC
4解析:重力做正功时,重力势能减少,重力做负功时,重力势能增大。因此只需要判断重力做正功还是做负功,即可判断出重力势能的变化。答案:C
5解析:垫片向右移动时,由于是轻弹簧,所以两弹簧产生的弹力相等,B正确;由于原长相同,劲度系数不同,所以两弹簧的长度不同;弹簧的弹性势能与形变量和劲度系数相关,则缓冲效果和劲度系数相关,C错,D正确.
答案:BD
6解析:拉力对绳子做正功,根据动能定理可知,重力必定做负功,重心应逐渐升高。
答案:A
7解析:从顶部注水必须使水被提高到A点后才能注入容器,但从底部注水,只要使水的高度提高到H+(将水看做质点,其位置在重心位置)即可,所以从顶部注水需要克服重力所做的功多。
答案:A8解析:本题的关键是抓住重力做功与重力势能变化的关系以及重力做功的特点,采用等效法分析。
从打开阀门K后,左管中的液体流向右管,直到两管液面相平,相当于把左管中高为的液体“搬”到右管中,其重心下降的高度为,所以该过程中,液体重力势能的减少量为ΔEp=ρgS·=ρgS(h2-h1)2。
答案:C
9解析:将铁棒竖立起来,其重心升高1
m,则重力势能增加mgh=200
J,人对铁棒所做的功至少应等于铁棒重力势能的增加量。
答案:200
J10解析:小球被弹出后做平抛运动,弹簧被压缩后弹性势能应等于小球做平抛运动的初动能。因此,可以测出小球离地面的竖直高度h,小球落地点的水平距离s,然后根据平抛运动的规律求出小球抛出时的初速度,即可求出弹簧被压缩后的弹性势能。小球做平抛运动时有h=gt2,s=vt,Ep=Ek=mv2=m·(s)2=。
答案:(1)小球离地面的竖直高度h,小球落地点的水平距离s
(2)
11解析:由于重力做功与通过的路径无关,只决定于物体的重力mg和物体初末位置的高度差,所以物体由A位置运动到B位置,虽然先运动到地面高度再回到B高度,但初末位置的高度差是(H-h),那么重力做的功就是W=mg(H-h)。
答案:mg(H-h)
12解析:(1)如图所示,1和2分别表示木块在刚没入水中时和到达池底时的位置。木块从1位置移到2位置,相当于使同体积的水从2移到1,所以池水势能的改变量等于这部分水在位置1和在位置2的势能之差。因为木块密度为水的,木块的质量为m,所以与木块同体积的水的质量为2m,故池水势能的改变量为
ΔE=2mg(H-a)。
(2)因为水池面积很大,可忽略因木块压入水中所引起的水深变化。木块刚好完全没入水中时,如图所示,原来处于划斜线区域的水被排开,后果等效于使这部分水平铺于水面,这部分水的质量为m,其势能的改变量为
ΔE水=mgH-mg(H-a)=mga
木块势能的改变量为
ΔE木=mg(H-)-mgH=-mga
根据动能定理,力F所做的功为
W=ΔE水+ΔE木=mga。
答案:(1)2mg(H-a) (2)mga
1如图所示,物体沿不同的路径从A运动到B,其中按不同的路径:①有摩擦作用;②无摩擦作用;③无摩擦,但有其他外力拉它。比较这三种情况下重力做的功W1、W2、W3,重力势能的变化量ΔEp1、ΔEp2、ΔEp3的关系,以下正确的是( )
A.W1>W2>W3
B.W1=W2=W3
C.ΔEp1=ΔEp2=ΔEp3
D.ΔEp1<ΔEp2<ΔEp3
2下列关于重力势能的说法中,错误的是( )
A.重力做正功,重力势能减少
B.重力做负功,重力势能增加
C.重力不做功,重力势能不变化
D.重力势能变化与重力做功无关
3用拉力F将一个重为5
N的物体匀速升高3
m,如图所示,在这个过程中,下列说法正确的是
…
( )
A.物体的重力做了15
J的功
B.拉力F对物体做了15
J的功
C.物体的重力势能增加了15
J
D.合力对物体做的功是15
J
4关于重力做功和重力势能变化,下列叙述正确的是( )
A.做竖直上抛运动的物体,在上升阶段,重力做负功,重力势能减少
B.做竖直上抛运动的物体,重力势能在不断减少
C.做平抛运动的物体,重力势能在不断减少
D.做匀速直线运动的物体,重力势能在不断减小
5某缓冲装置可抽象成如图所示的简单模型.图中K1、K2为原长相等,劲度系数不同的轻质弹簧。下列表述正确的是( )
A.缓冲效果与弹簧的劲度系数无关
B.垫片向右移动时,两弹簧产生的弹力大小相等
C.垫片向右移动时,两弹簧的长度保持相等
D.垫片向右移动时,两弹簧的弹性势能发生改变
6一质量均匀的不可伸长的绳索(重力不可忽略),A、B两端固定在天花板上,如图所示。今在最低点C施加一竖直向下的力将绳索拉至D点,在此过程中,绳索的重心位置将( )
A.逐渐升高
B.逐渐降低
C.先降低后升高
D.始终不变
7如图所示,水塔是在空中的盛水容器,有两个注水口,一个在顶部,一个在底部,注满一水塔水。则
…( )
A.从顶部注水做功多
B.从底部注水做功少
C.从两注水口注水做功一样多
D.条件不足,不能比较从哪个注水口注水做功多少
8如图所示,将横截面积为S的玻璃管弯成连通器,放在水平桌面上,左、右管处在竖直状态,先关闭阀门K,往左、右管中分别注入高度为h1和h2、密度为ρ的液体,然后打开阀门K,直到液体静止。在上述过程中,液体的重力势能减少了( )
A.ρgS(h1-h2)
B.ρgS(h1-h2)2
C.ρgS(h1-h2)2
D.ρgS(h1-h2)
9一根长为2
m、质量为20
kg的均匀细铁棒横卧在水平地面上,人若要将它完全竖立起来,人对铁棒所做的功不能少于______。
10为了测定一根轻弹簧压缩最短时能储存的弹性势能大小,可以将弹簧固定在一带有凹槽轨道一端,并将轨道固定在水平桌面边缘上,如图所示,用钢球将弹簧压缩至最短,而后突然释放,钢球将沿轨道飞出桌面,实验时:
(1)需要测定的物理量________。
(2)计算弹簧最短时弹性势能的关系式是Ep=________。
11如图所示,求质量为m的小球从位置A运动到位置B的过程中重力所做的功。
12面积很大的水池,水深为H,水面上浮着一正方体木块。木块边长为a,密度为水的,质量为m。开始时,木块静止,有一半没入水中,如图所示。现用力F将木块缓慢地压到池底。不计摩擦。求:
(1)从木块刚好完全没入水中到停在池底的过程中,池水势能的改变量;
(2)从开始到木块刚好完全没入水的过程中,力F所做的功。
参考答案
1解析:重力做功与路径无关,取决于物体初、末位置,且与受不受其他力无关。重力势能的变化量只取决于重力做的功,因此,三种情况下重力做功相同,重力势能的变化量也相同。
答案:BC
2解析:重力势能变化取决于重力的做功情况。重力对物体做正功时,重力势能减小,物体克服重力做功,即重力做负功时,重力势能增加,且重力势能的变化量应等于重力所做功的负值,所以选项D错误。
答案:D
3解析:物体上升,重力做负功,WG=-mgh=-5×3
J=-15
J,选项A错误;因为物体匀速上升,所以拉力F=G=5
N,则拉力做功WF=Fh=5×3
J=15
J,选项B正确;因物体克服重力做功15
J,故物体重力势能增加15
J,选项C正确;因为物体匀速上升,合力为零,则合力不做功,选项D错误。
答案:BC
4解析:重力做正功时,重力势能减少,重力做负功时,重力势能增大。因此只需要判断重力做正功还是做负功,即可判断出重力势能的变化。答案:C
5解析:垫片向右移动时,由于是轻弹簧,所以两弹簧产生的弹力相等,B正确;由于原长相同,劲度系数不同,所以两弹簧的长度不同;弹簧的弹性势能与形变量和劲度系数相关,则缓冲效果和劲度系数相关,C错,D正确.
答案:BD
6解析:拉力对绳子做正功,根据动能定理可知,重力必定做负功,重心应逐渐升高。
答案:A
7解析:从顶部注水必须使水被提高到A点后才能注入容器,但从底部注水,只要使水的高度提高到H+(将水看做质点,其位置在重心位置)即可,所以从顶部注水需要克服重力所做的功多。
答案:A8解析:本题的关键是抓住重力做功与重力势能变化的关系以及重力做功的特点,采用等效法分析。
从打开阀门K后,左管中的液体流向右管,直到两管液面相平,相当于把左管中高为的液体“搬”到右管中,其重心下降的高度为,所以该过程中,液体重力势能的减少量为ΔEp=ρgS·=ρgS(h2-h1)2。
答案:C
9解析:将铁棒竖立起来,其重心升高1
m,则重力势能增加mgh=200
J,人对铁棒所做的功至少应等于铁棒重力势能的增加量。
答案:200
J10解析:小球被弹出后做平抛运动,弹簧被压缩后弹性势能应等于小球做平抛运动的初动能。因此,可以测出小球离地面的竖直高度h,小球落地点的水平距离s,然后根据平抛运动的规律求出小球抛出时的初速度,即可求出弹簧被压缩后的弹性势能。小球做平抛运动时有h=gt2,s=vt,Ep=Ek=mv2=m·(s)2=。
答案:(1)小球离地面的竖直高度h,小球落地点的水平距离s
(2)
11解析:由于重力做功与通过的路径无关,只决定于物体的重力mg和物体初末位置的高度差,所以物体由A位置运动到B位置,虽然先运动到地面高度再回到B高度,但初末位置的高度差是(H-h),那么重力做的功就是W=mg(H-h)。
答案:mg(H-h)
12解析:(1)如图所示,1和2分别表示木块在刚没入水中时和到达池底时的位置。木块从1位置移到2位置,相当于使同体积的水从2移到1,所以池水势能的改变量等于这部分水在位置1和在位置2的势能之差。因为木块密度为水的,木块的质量为m,所以与木块同体积的水的质量为2m,故池水势能的改变量为
ΔE=2mg(H-a)。
(2)因为水池面积很大,可忽略因木块压入水中所引起的水深变化。木块刚好完全没入水中时,如图所示,原来处于划斜线区域的水被排开,后果等效于使这部分水平铺于水面,这部分水的质量为m,其势能的改变量为
ΔE水=mgH-mg(H-a)=mga
木块势能的改变量为
ΔE木=mg(H-)-mgH=-mga
根据动能定理,力F所做的功为
W=ΔE水+ΔE木=mga。
答案:(1)2mg(H-a) (2)mga
同课章节目录
- 第一章 怎样研究抛体运动
- 1 飞机投弹与平抛运动
- 2 研究平抛运动的规律
- 3 研究斜抛运动
- 第二章 研究圆周运动
- 1 怎样描述圆周运动
- 2 研究匀速圆周运动的规律
- 3 圆周运动的案例分析
- 4 研究离心现象及其应用
- 第三章 动能的变化与机械功
- 1 探究动能变化跟功的关系
- 2 研究功与功率
- 3 动能定理的应用
- 第四章 能量守恒与可持续发展
- 1 势能的变化与机械功
- 2 研究机械能守恒定律
- 3 能量的转化与守恒
- 4 能源与可持续发展
- 第五章 万有引力与航天
- 1 从托勒密到开普勒
- 2 万有引力定律是怎样发现的
- 3 万有引力定律与天文学的新发现
- 4 飞出地球去
- 第六章 经典力学与现代物理
- 1 经典力学的巨大成就和局限性
- 2 狭义相对论的基本原理
- 3 爱因斯坦心目中的宇宙
- 4 微观世界与量子论
