5.7 切线长定理 课件(19张PPT)
文档属性
| 名称 | 5.7 切线长定理 课件(19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 124.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-25 00:00:00 | ||
图片预览




文档简介
课件19张PPT。切线长定理及
三角形的内切圆大中分校初三数学备课组
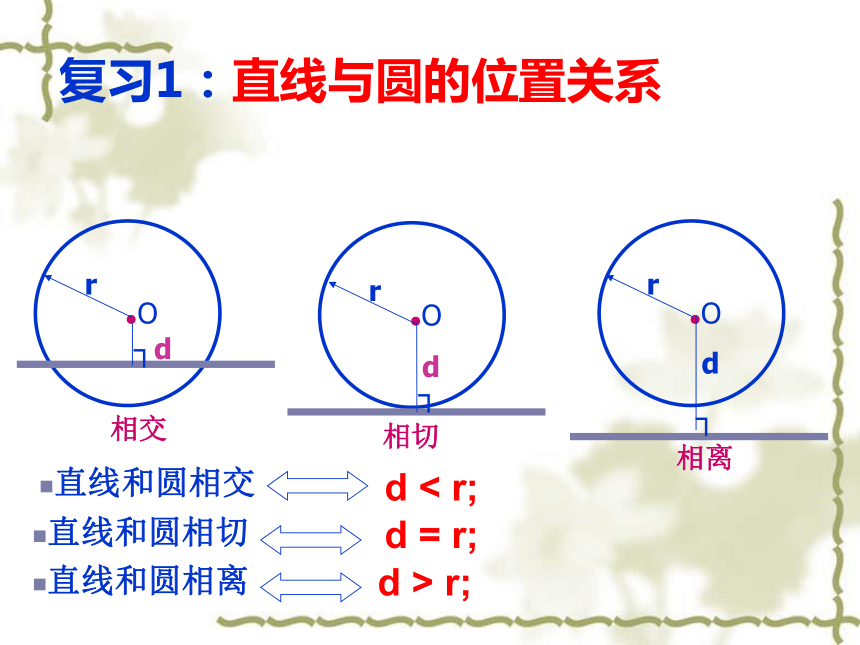
复习1:直线与圆的位置关系直线和圆相交
d < r;直线和圆相切
直线和圆相离
d = r;d > r;复习2:
1、切线的判定定理是什么?
2、切线的性质定理是什么
3、角平分线的性质是什么?
4、什么叫三角形的外接圆和外心?外心是三角形什么的交点?
我们知道,过圆上一点可以作圆的一条切线,那么过圆外一点可以作圆的几条切线呢?
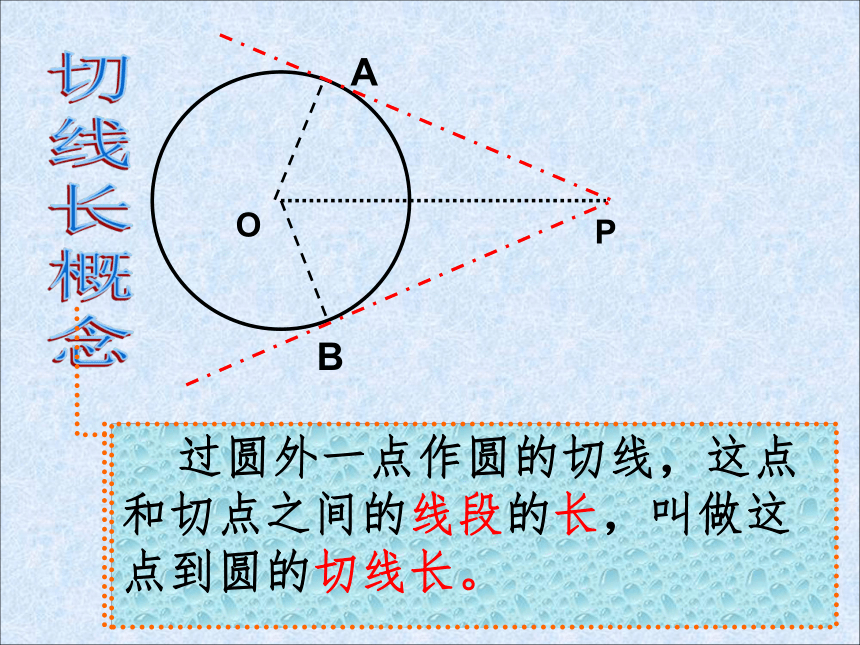
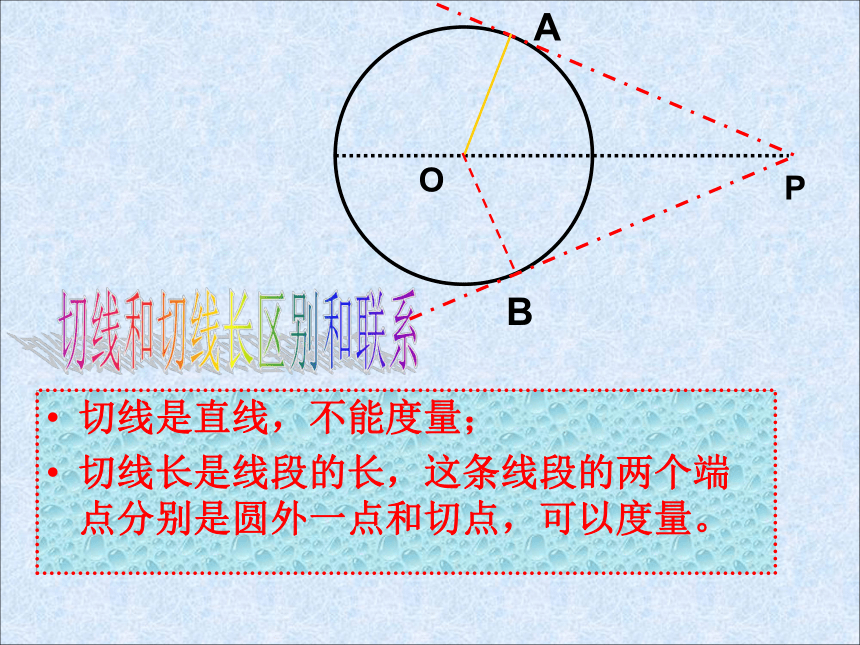
探究:切线长概念 过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。OPAB切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。切线和切线长区别和联系探究: 从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。PA = PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB试用文字语言叙述你所发现的结论
PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理思考:
如何在一块三角形的铁皮上截下一块圆形的用料,并且使得圆的面积尽可能大?.o.o..o外切圆圆心:三角形三边垂直平分线的交点。
外切圆的半径:交点到三角形任意一个顶点的距离。三角形外接圆三角形内切圆内切圆圆心:三角形三个内角平分线的交点。
内切圆的半径:交点到三角形任意一边的垂直距离。AABBCC当堂检测 :
1、在⊿ABC中,∠A=50°
(1)若点O是⊿ABC的外心,则∠BOC= .
(2) 若点O是⊿ABC的内心,则∠BOC= .
2、如图,PA,PB是⊙O的切线,A,B为切点,∠OPB=30°.
(1)∠APB的度数是 ;
(2)当OA=3时,AP= . .
例1. (1) 已知:如图, △ABC的内切圆⊙O与BC 、CA、 AB 分别相交于点D 、E 、F ,且AB=9厘米,BC =14厘米,CA =13厘米,求AF、BD、CE的长。
O例2. 如图,四边形ABCD的边 AB、BC、CD、DA和⊙O分别相切于L、M、N、P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?解:∵ AB,BC,CD,DA都与⊙O相切,
L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等(可做定理用)1、已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。60练 习:8cm6cm4cm6cmr练习:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。探究 直角三角形的两直角边分别是a,b ,斜边是c,则其内切圆的半径r与三边的关系是什么?2cm.1、切线长的定义
2、切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 小 结:∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPBOP垂直平分AB 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。3、三角形的内切圆和内心
4 、圆的外切四边形的两组对边的和相等作业布置
三角形的内切圆大中分校初三数学备课组
复习1:直线与圆的位置关系直线和圆相交
d < r;直线和圆相切
直线和圆相离
d = r;d > r;复习2:
1、切线的判定定理是什么?
2、切线的性质定理是什么
3、角平分线的性质是什么?
4、什么叫三角形的外接圆和外心?外心是三角形什么的交点?
我们知道,过圆上一点可以作圆的一条切线,那么过圆外一点可以作圆的几条切线呢?
探究:切线长概念 过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长。OPAB切线是直线,不能度量;
切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量。切线和切线长区别和联系探究: 从⊙O外的一点引两条切线PA,PB,切点分别是A、B,连结OA、OB、OP,你能发现什么结论?并证明你所发现的结论。PA = PB∠OPA=∠OPB证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP
∴Rt△AOP≌Rt△BOP(HL)
∴ PA = PB ∠OPA=∠OPB试用文字语言叙述你所发现的结论
PA、PB分别切⊙O于A、BPA = PB∠OPA=∠OPB 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 切线长定理思考:
如何在一块三角形的铁皮上截下一块圆形的用料,并且使得圆的面积尽可能大?.o.o..o外切圆圆心:三角形三边垂直平分线的交点。
外切圆的半径:交点到三角形任意一个顶点的距离。三角形外接圆三角形内切圆内切圆圆心:三角形三个内角平分线的交点。
内切圆的半径:交点到三角形任意一边的垂直距离。AABBCC当堂检测 :
1、在⊿ABC中,∠A=50°
(1)若点O是⊿ABC的外心,则∠BOC= .
(2) 若点O是⊿ABC的内心,则∠BOC= .
2、如图,PA,PB是⊙O的切线,A,B为切点,∠OPB=30°.
(1)∠APB的度数是 ;
(2)当OA=3时,AP= . .
例1. (1) 已知:如图, △ABC的内切圆⊙O与BC 、CA、 AB 分别相交于点D 、E 、F ,且AB=9厘米,BC =14厘米,CA =13厘米,求AF、BD、CE的长。
O例2. 如图,四边形ABCD的边 AB、BC、CD、DA和⊙O分别相切于L、M、N、P。
(1)图中有几对相等的线段?(2)由此你能发现什么结论? 为什么?解:∵ AB,BC,CD,DA都与⊙O相切,
L,M,N,P是切点,∴AL=AP,LB=MB,
DN=DP,NC=MC∴AL+ LB+ DN+ NC = AP+ MB+DP+MC即 AB+ CD = AD+BC圆的外切四边形的两组对边的和相等(可做定理用)1、已知⊙O的半径为3cm,点P和圆心O的距离为6cm,经过点P有⊙O的两条切线,则切线长为______cm。这两条切线的夹角为_____度。60练 习:8cm6cm4cm6cmr练习:直角三角形的两直角边分别是5cm,12cm 则其内切圆的半径为______。探究 直角三角形的两直角边分别是a,b ,斜边是c,则其内切圆的半径r与三边的关系是什么?2cm.1、切线长的定义
2、切线长定理 从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。 小 结:∵PA、PB分别切⊙O于A、B∴PA = PB ,∠OPA=∠OPBOP垂直平分AB 切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。3、三角形的内切圆和内心
4 、圆的外切四边形的两组对边的和相等作业布置
