19.2平行四边形的判定公开课课件
图片预览




文档简介
课件23张PPT。18.1.2 平行四边形的判定
第一课时
有两组对边分别平行的四边形叫做平行四边形2、平行四边形的性质:平行四边形的性质定理1:
平行四边形的对边相等平行四边形的性质定理2:
平行四边形的对角相等平行四边形的性质定理3:
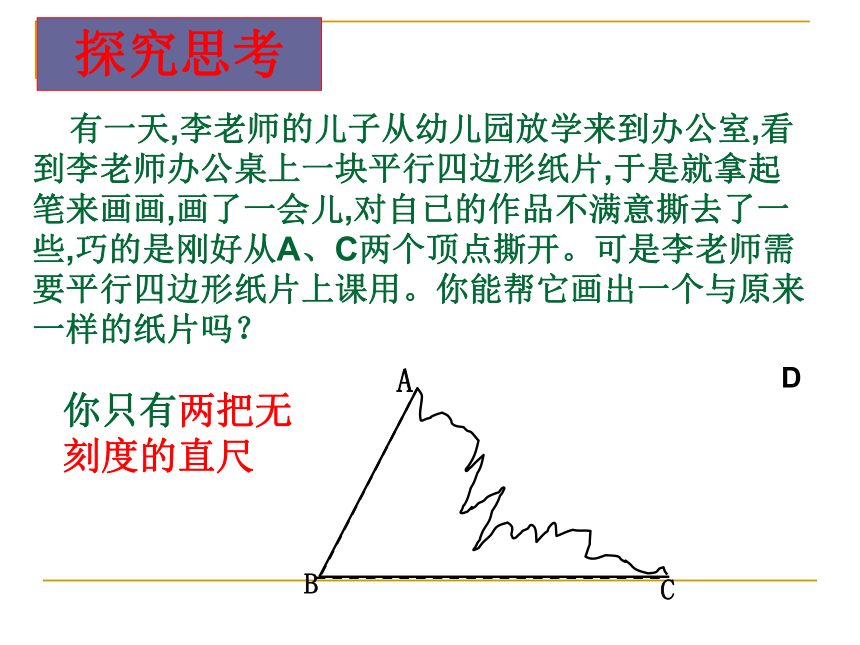
平行四边形的对角线互相平分1、平行四边形的定义:复习旧知如何判断四边形是否是平行四边形呢? 有一天,李老师的儿子从幼儿园放学来到办公室,看到李老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。可是李老师需要平行四边形纸片上课用。你能帮它画出一个与原来一样的纸片吗?D探究思考你只有两把无刻度的直尺平行四边形的定义:
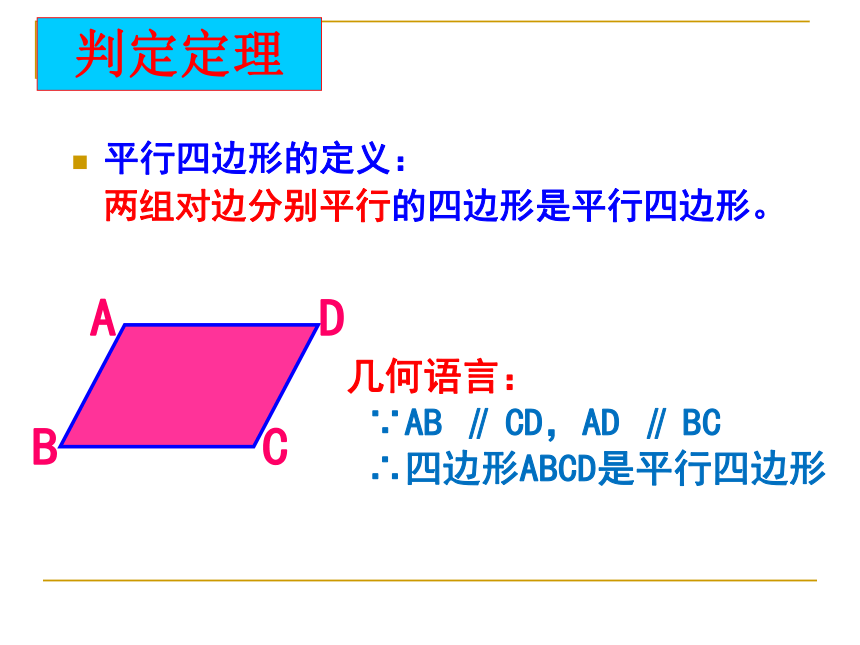
两组对边分别平行的四边形是平行四边形。几何语言:
∵AB ∥ CD,AD ∥ BC
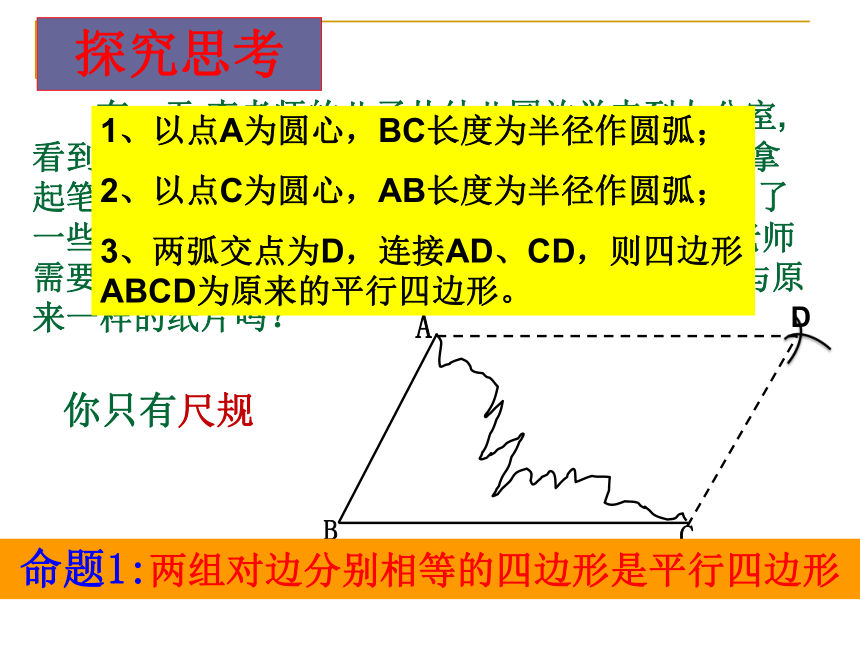
∴四边形ABCD是平行四边形判定定理D探究思考通过以上活动你得到了什么结论? 命题1:两组对边分别相等的四边形是平行四边形 有一天,李老师的儿子从幼儿园放学来到办公室,看到李老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。可是李老师需要平行四边形纸片上课用。你能帮它画出一个与原来一样的纸片吗?你只有尺规1、以点A为圆心,BC长度为半径作圆弧;
2、以点C为圆心,AB长度为半径作圆弧;
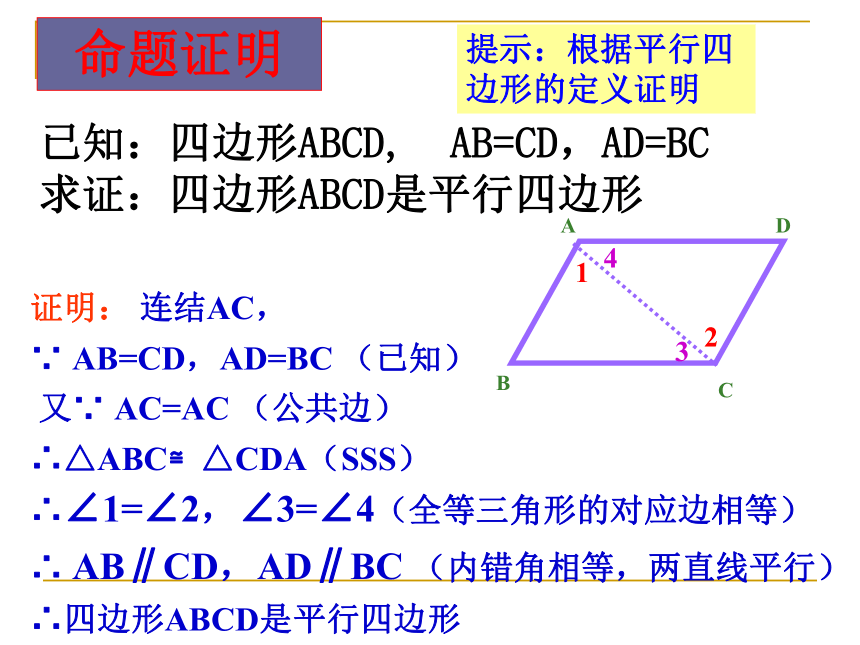
3、两弧交点为D,连接AD、CD,则四边形ABCD为原来的平行四边形。BDAC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形2134证明: 连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
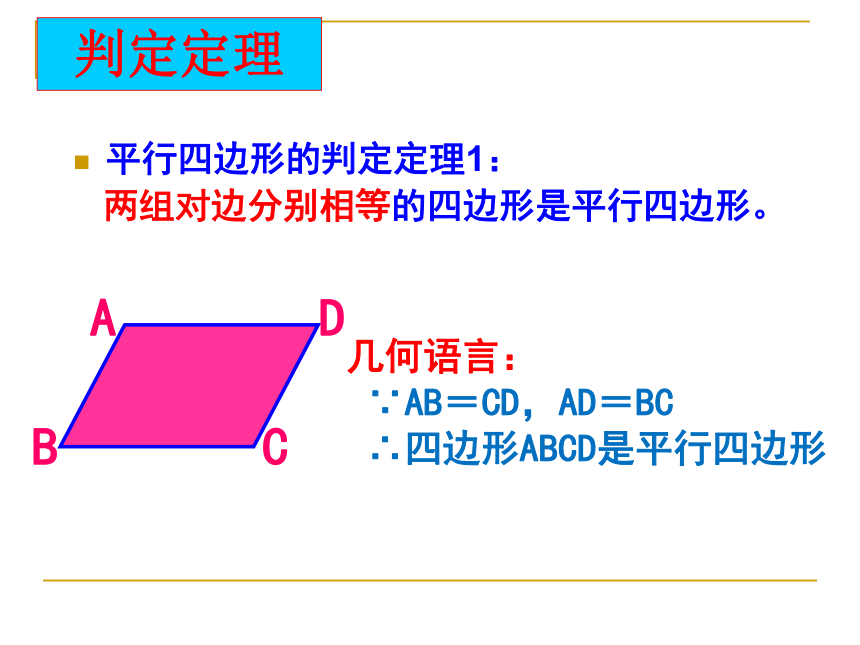
∴四边形ABCD是平行四边形命题证明提示:根据平行四边形的定义证明平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。几何语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形判定定理 发现了吗?探究思考命题2:两组对角相等的四边形是平行四边形。平行四边形的判定定理1和
平行四边形的性质定理1什么什么关系?互逆定理平行四边形性质定理2和3的逆命题会不会也分别和性质定理2、3有这样的关系呢?命题3:对角线互相平分的四边形是平行四边形。 依次证明试试性质2:平行四边形的对角相等。性质3:平行四边形的对角线互相平分。 BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形证明:
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形命题证明平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。几何语言:
∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形判定定理已知:四边形ABCD中, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形证法一:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是
平行四边形)∴ ∠3 = ∠4命题证明还有其它方法吗?已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证法二:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
命题证明平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形。几何语言:
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形判定定理还有其它判定方法吗?小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
四边形ABCD是平行四边形命题4:一组对边平行且相等的四边形是 平行四边形 探究思考已知:四边形ABCD中 AB∥CD, AB=CD求证:四边形ABCD是平行四边形证明:连接BD∵ AB∥CD∴∠ABD = ∠ CDB又∵AB =CD ,BD = DB∴△ABD ≌△CDB (SAS)∴AD = CB∴四边形ABCD是平行四边形又∵AB =CD 命题证明平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形
几何语言:
∵ AB∥CD, AB=CD
∴四边形ABCD是平行四边形判定定理例1 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO,AO=CO
又∵AE=CF
∴AO-AE=CO-CF
即:EO=FO
∴ 四边形BFDE是平行四边形
例题讲解证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB//DF
∵ E,F分别是边AB,CD的中点,
∴BE=DF
∴四边形AECF是平行四边形.例2 已知: ABCD中,E,F分别是边AB,CD的中点,
求证:四边形AECF是平行四边形.例题讲解 在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且BE=DF”,结论是否
仍然成立?请说明理由. 在上题中,将“E,F分别是AB,CD的中点”改为
“DE,BF分别是∠BAD、∠BCD的角平分线”,结论是否仍然成立?请说明理由.1、如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?AB ∥ DC∥ EFAD ∥ BCDE ∥ CF课堂练习证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD//BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形. 课堂练习3、已知:如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.课堂练习证明:∵DF//BE
∴∠DFC=∠BEA
∴∠AFD=1800-∠ DFC
=1800-∠ BEA= ∠BEC
又∵ AF=CE,DF=BE
∴△AFD≌△CEB
∴AD=BC, ∠DAF=∠BCE
∴AD//BC
∴四边形ABCD是平行四边形. 两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.从角考虑 判定一个四边形是平行四边形可从哪些角度思考?具体有哪些方法? 课堂小结 两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形. 从对角线考虑 谢谢指导作业布置:
1、必做题:习题18.1第5、6题;
2、选做题:习题18.1第7、8题。
第一课时
有两组对边分别平行的四边形叫做平行四边形2、平行四边形的性质:平行四边形的性质定理1:
平行四边形的对边相等平行四边形的性质定理2:
平行四边形的对角相等平行四边形的性质定理3:
平行四边形的对角线互相平分1、平行四边形的定义:复习旧知如何判断四边形是否是平行四边形呢? 有一天,李老师的儿子从幼儿园放学来到办公室,看到李老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。可是李老师需要平行四边形纸片上课用。你能帮它画出一个与原来一样的纸片吗?D探究思考你只有两把无刻度的直尺平行四边形的定义:
两组对边分别平行的四边形是平行四边形。几何语言:
∵AB ∥ CD,AD ∥ BC
∴四边形ABCD是平行四边形判定定理D探究思考通过以上活动你得到了什么结论? 命题1:两组对边分别相等的四边形是平行四边形 有一天,李老师的儿子从幼儿园放学来到办公室,看到李老师办公桌上一块平行四边形纸片,于是就拿起笔来画画,画了一会儿,对自已的作品不满意撕去了一些,巧的是刚好从A、C两个顶点撕开。可是李老师需要平行四边形纸片上课用。你能帮它画出一个与原来一样的纸片吗?你只有尺规1、以点A为圆心,BC长度为半径作圆弧;
2、以点C为圆心,AB长度为半径作圆弧;
3、两弧交点为D,连接AD、CD,则四边形ABCD为原来的平行四边形。BDAC已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形2134证明: 连结AC,
∵ AB=CD,AD=BC (已知)
又∵ AC=AC (公共边)
∴△ABC≌△CDA(SSS)∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形命题证明提示:根据平行四边形的定义证明平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形。几何语言:
∵AB=CD,AD=BC
∴四边形ABCD是平行四边形判定定理 发现了吗?探究思考命题2:两组对角相等的四边形是平行四边形。平行四边形的判定定理1和
平行四边形的性质定理1什么什么关系?互逆定理平行四边形性质定理2和3的逆命题会不会也分别和性质定理2、3有这样的关系呢?命题3:对角线互相平分的四边形是平行四边形。 依次证明试试性质2:平行四边形的对角相等。性质3:平行四边形的对角线互相平分。 BDAC已知:四边形ABCD, ∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形证明:
∵∠A=∠C,∠B=∠D(已知)
又∵∠A+ ∠B+ ∠C+ ∠D =360 °
∴ 2∠A+ 2∠B=360 °即∠A+ ∠B=180 °
∴ AD∥BC (同旁内角互补,两直线平行)同理可证AB∥CD
∴四边形ABCD是平行四边形命题证明平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形。几何语言:
∵ ∠A=∠C,∠B=∠D
∴四边形ABCD是平行四边形判定定理已知:四边形ABCD中, AC、BD交于点O
且OA=OC,OB=OD
求证:四边形ABCD是平行四边形证法一:∵ AO = CO ,BO = DO ,∠1 = ∠2∴△AOB≌△COD∴AB ∥ CD 同理AD ∥ BC∴四边形ABCD是平行四边形
(两组对边分别平行的四边形是
平行四边形)∴ ∠3 = ∠4命题证明还有其它方法吗?已知:如图,四边形对角线相交于点o,
且OA=OC、OB=OD.
求证:四边形ABCD是平行四边形证法二:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四 边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。)
命题证明平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形。几何语言:
∵ OA=OC,OB=OD
∴四边形ABCD是平行四边形判定定理还有其它判定方法吗?小明的爸爸在钉制一个框架时采用了下面的方法:
将两根同样长的木条AB,CD平行放置,再用两根木条AD,BC加固,得到的这个四边形ABCD是什么样的图形?
四边形ABCD是平行四边形命题4:一组对边平行且相等的四边形是 平行四边形 探究思考已知:四边形ABCD中 AB∥CD, AB=CD求证:四边形ABCD是平行四边形证明:连接BD∵ AB∥CD∴∠ABD = ∠ CDB又∵AB =CD ,BD = DB∴△ABD ≌△CDB (SAS)∴AD = CB∴四边形ABCD是平行四边形又∵AB =CD 命题证明平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形
几何语言:
∵ AB∥CD, AB=CD
∴四边形ABCD是平行四边形判定定理例1 已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DABCEF证明:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ BO=DO,AO=CO
又∵AE=CF
∴AO-AE=CO-CF
即:EO=FO
∴ 四边形BFDE是平行四边形
例题讲解证明:∵四边形ABCD是平行四边形,
∴AB=CD,EB//DF
∵ E,F分别是边AB,CD的中点,
∴BE=DF
∴四边形AECF是平行四边形.例2 已知: ABCD中,E,F分别是边AB,CD的中点,
求证:四边形AECF是平行四边形.例题讲解 在上题中,将“E,F分别是AB,CD的中点”改为
“E,F分别是AB,CD上的点,且BE=DF”,结论是否
仍然成立?请说明理由. 在上题中,将“E,F分别是AB,CD的中点”改为
“DE,BF分别是∠BAD、∠BCD的角平分线”,结论是否仍然成立?请说明理由.1、如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?AB ∥ DC∥ EFAD ∥ BCDE ∥ CF课堂练习证明:∵四边形ABCD是平行四边形.
∴OA=OC,AD//BC,
∴∠AEF=∠CFE
又∵∠AOE=∠COF
∴△AOE≌△COF
∴OE=OF
∴四边形AECF是平行四边形. 课堂练习3、已知:如图,E、F是四边形ABCD的对角线AC上两点,AF=CE,DF=BE,DF∥BE.
求证:四边形ABCD是平行四边形.课堂练习证明:∵DF//BE
∴∠DFC=∠BEA
∴∠AFD=1800-∠ DFC
=1800-∠ BEA= ∠BEC
又∵ AF=CE,DF=BE
∴△AFD≌△CEB
∴AD=BC, ∠DAF=∠BCE
∴AD//BC
∴四边形ABCD是平行四边形. 两组对边分别平行的四边形是平行四边形;
两组对边分别相等的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.从角考虑 判定一个四边形是平行四边形可从哪些角度思考?具体有哪些方法? 课堂小结 两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形. 从对角线考虑 谢谢指导作业布置:
1、必做题:习题18.1第5、6题;
2、选做题:习题18.1第7、8题。
