初中数学苏科版 几何最值问题面面观 教学案(含答案)
文档属性
| 名称 | 初中数学苏科版 几何最值问题面面观 教学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 308.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-26 00:00:00 | ||
图片预览

文档简介
初中数学几何最值问题面面观
在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为几何最值问题.近年来,各地中考题常通过几何最值问题考查学生的实践操作能力、空间想象能力、分析问题和解决问题的能力.本文针对不同类型的几何最值问题作一总结与分析,希望对大家有所帮助.
最值问题的解决方法通常有如下两大类:
一、应用几何性质
1.三角形的三边关系
例1
如图1,,矩形的顶点、分别在边上.当分在边上运动时,随之在边上运动,矩形的形状保持不变,其中,运动过程中,点到点的最大距离为(
)
(A)
(B)
(c)
(D)
分析
如图1,取的中点,连结.
,
当三点共线时,点到点的距离最大,此时,,
.,
Z
的最大值为.
故选A.
2.两点间线段最短
例2
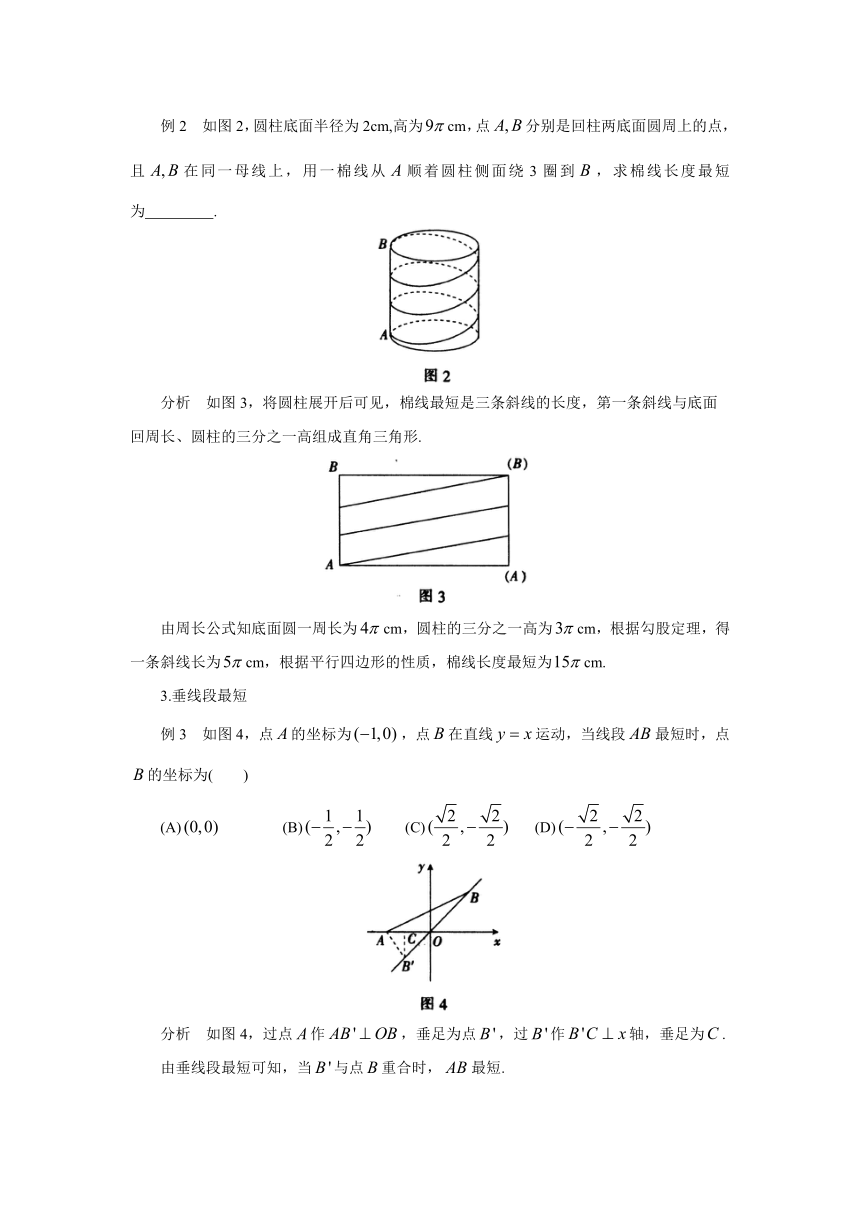
如图2,圆柱底面半径为2cm,高为cm,点分别是回柱两底面圆周上的点,
且在同一母线上,用一棉线从顺着圆柱侧面绕3圈到,求棉线长度最短为
.
分析
如图3,将圆柱展开后可见,棉线最短是三条斜线的长度,第一条斜线与底面
回周长、圆柱的三分之一高组成直角三角形.
由周长公式知底面圆一周长为cm,圆柱的三分之一高为cm,根据勾股定理,得一条斜线长为cm,根据平行四边形的性质,棉线长度最短为cm.
3.垂线段最短
例3
如图4,点的坐标为,点在直线运动,当线段最短时,点的坐标为(
)
(A)
(B)
(C)
(D)
分析
如图4,过点作,垂足为点,过作轴,垂足为.
由垂线段最短可知,当与点重合时,最短.
∵点在直线上运动,
∴是等腰直角三角形
∴为等腰直角三角形
∵点的坐标为,
,
的坐标为
∴当线段最短时,点的坐标为
故选B.
4.利用轴对称
例4
如图5,正方形,,是的中点,点是对角线上一动点,则的最小值为
.
分析
连结,交于点,连结.
∵点与点关于对称,
∴的长即为的小值
,是的中点,
在中
二、代数证法
1.利用配方法
例5
如图6是半圆与矩形结合而成的窗户,如果窗户的周长为8米,怎样才能得出最大面积,使得窗户透光最好
分析
设表示半圆半径,表示矩形边长,则有,
于是,
①
若窗户的最大面积为,则
②
把①代入②,有
.
上式中,只有时,等号成立.
这时,由①有
,
即当窗户周长一定时,窗户下部矩形宽恰为半径时,窗户面积最大.
2.利用一元二次方程根的判别式
例6
已知:,且,求的最小值.
解
令,
代入,
,
去分母,整理,得
∵为实数,
或
∵,
.
故的最小值为8.
在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为几何最值问题.近年来,各地中考题常通过几何最值问题考查学生的实践操作能力、空间想象能力、分析问题和解决问题的能力.本文针对不同类型的几何最值问题作一总结与分析,希望对大家有所帮助.
最值问题的解决方法通常有如下两大类:
一、应用几何性质
1.三角形的三边关系
例1
如图1,,矩形的顶点、分别在边上.当分在边上运动时,随之在边上运动,矩形的形状保持不变,其中,运动过程中,点到点的最大距离为(
)
(A)
(B)
(c)
(D)
分析
如图1,取的中点,连结.
,
当三点共线时,点到点的距离最大,此时,,
.,
Z
的最大值为.
故选A.
2.两点间线段最短
例2
如图2,圆柱底面半径为2cm,高为cm,点分别是回柱两底面圆周上的点,
且在同一母线上,用一棉线从顺着圆柱侧面绕3圈到,求棉线长度最短为
.
分析
如图3,将圆柱展开后可见,棉线最短是三条斜线的长度,第一条斜线与底面
回周长、圆柱的三分之一高组成直角三角形.
由周长公式知底面圆一周长为cm,圆柱的三分之一高为cm,根据勾股定理,得一条斜线长为cm,根据平行四边形的性质,棉线长度最短为cm.
3.垂线段最短
例3
如图4,点的坐标为,点在直线运动,当线段最短时,点的坐标为(
)
(A)
(B)
(C)
(D)
分析
如图4,过点作,垂足为点,过作轴,垂足为.
由垂线段最短可知,当与点重合时,最短.
∵点在直线上运动,
∴是等腰直角三角形
∴为等腰直角三角形
∵点的坐标为,
,
的坐标为
∴当线段最短时,点的坐标为
故选B.
4.利用轴对称
例4
如图5,正方形,,是的中点,点是对角线上一动点,则的最小值为
.
分析
连结,交于点,连结.
∵点与点关于对称,
∴的长即为的小值
,是的中点,
在中
二、代数证法
1.利用配方法
例5
如图6是半圆与矩形结合而成的窗户,如果窗户的周长为8米,怎样才能得出最大面积,使得窗户透光最好
分析
设表示半圆半径,表示矩形边长,则有,
于是,
①
若窗户的最大面积为,则
②
把①代入②,有
.
上式中,只有时,等号成立.
这时,由①有
,
即当窗户周长一定时,窗户下部矩形宽恰为半径时,窗户面积最大.
2.利用一元二次方程根的判别式
例6
已知:,且,求的最小值.
解
令,
代入,
,
去分母,整理,得
∵为实数,
或
∵,
.
故的最小值为8.
同课章节目录
