第十章平行线、相交线与平移单元检测试题
文档属性
| 名称 | 第十章平行线、相交线与平移单元检测试题 |

|
|
| 格式 | doc | ||
| 文件大小 | 348.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-26 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
沪科版七年级下册数学第十章平行线、相交线与平移单元检测试题
一、选择题(本大题共10小题)
1. 下列说法正确的是( )
A.两点之间的距离是两点间的线段
B.同一平面内,过一点有且只有一条直线与已知直线平行
C.与同一条直线垂直的两条直线也垂直
D.同一平面内,过一点有且只有一条直线与已知直线垂直
2. a,b,c是同一平面内任意三条直线,交点可能有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.都不对
3.在以下现象中,属于平移的是( )
①在挡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动.
A.①② B.①③ C.②③ D.②④
4. 已知:如图,直线a∥b,AC⊥AB于A,AC交直线b于点C,∠1=46°,则∠2的度数是( )
A.50° B.45° C.44° D.30°
5. 已知∠A的两边与∠B的两边互相平行,且∠A=20°,则∠B的度数为( )
A.20° B.80° C.160° D.20°或160°
6. 如图,有三条公路,其中AC与AB垂直,小明和小亮分别从A,B两点沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是( )
A.小亮骑车的速度快
B.小明骑车的速度快
C.两人骑车的速度一样快
D.因为不知道公路的长度,所以无法判断他们骑车速度的快慢
7. 某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次左拐50°,第二次左拐120°
8. 如图,直线l1∥l2,则下列式子成立的是( )
A.∠1+∠2+∠3=180° B.∠1﹣∠2+∠3=180°
C.∠2+∠3﹣∠1=180° D.∠1+∠2﹣∠3=180°
9. 如图,如果AB ∥CD ,则∠α,∠β,∠γ之间的关系是 ( )
A. ∠α+∠β+∠γ=180° B. ∠α-∠β+∠γ=180°
C.∠α+∠β-∠γ=180° D.∠α+∠β+∠γ=270°
10. 小明同学把一个含有450角的直角三角板在如图所示的两条平行线上,测得,则的度数是( )
A.450 B.550 C.650 D.750
二、填空题(本大题共8小题)
11. 如图,直线a∥b,则∠ACB= 度.
12.如图在一块长为12cm,宽为6cm的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm)则空白部分表示的草地面积是 。
13. 如图,一张宽度相等的纸条,折叠后,若∠ABC=120°,则∠1的度数为 .
14. 如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为 .
15.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 。
16. 如图,直线CD、EF相交于点O,则∠1+∠2+∠3的度数是 度.
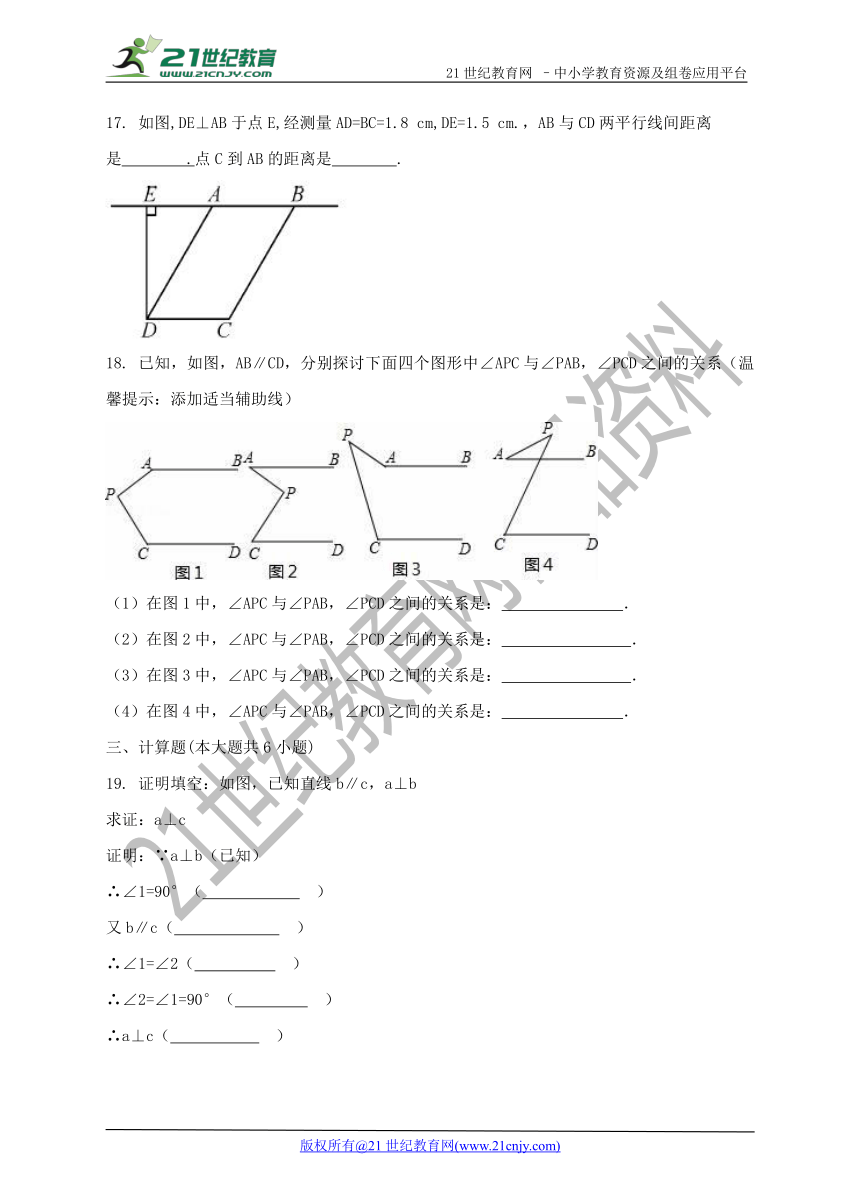
17. 如图,DE⊥AB于点E,经测量AD=BC=1.8 cm,DE=1.5 cm.,AB与CD两平行线间距离是 .点C到AB的距离是 .
18. 已知,如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系(温馨提示:添加适当辅助线)
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是: .
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是: .
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是: .
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是: .
三、计算题(本大题共6小题)
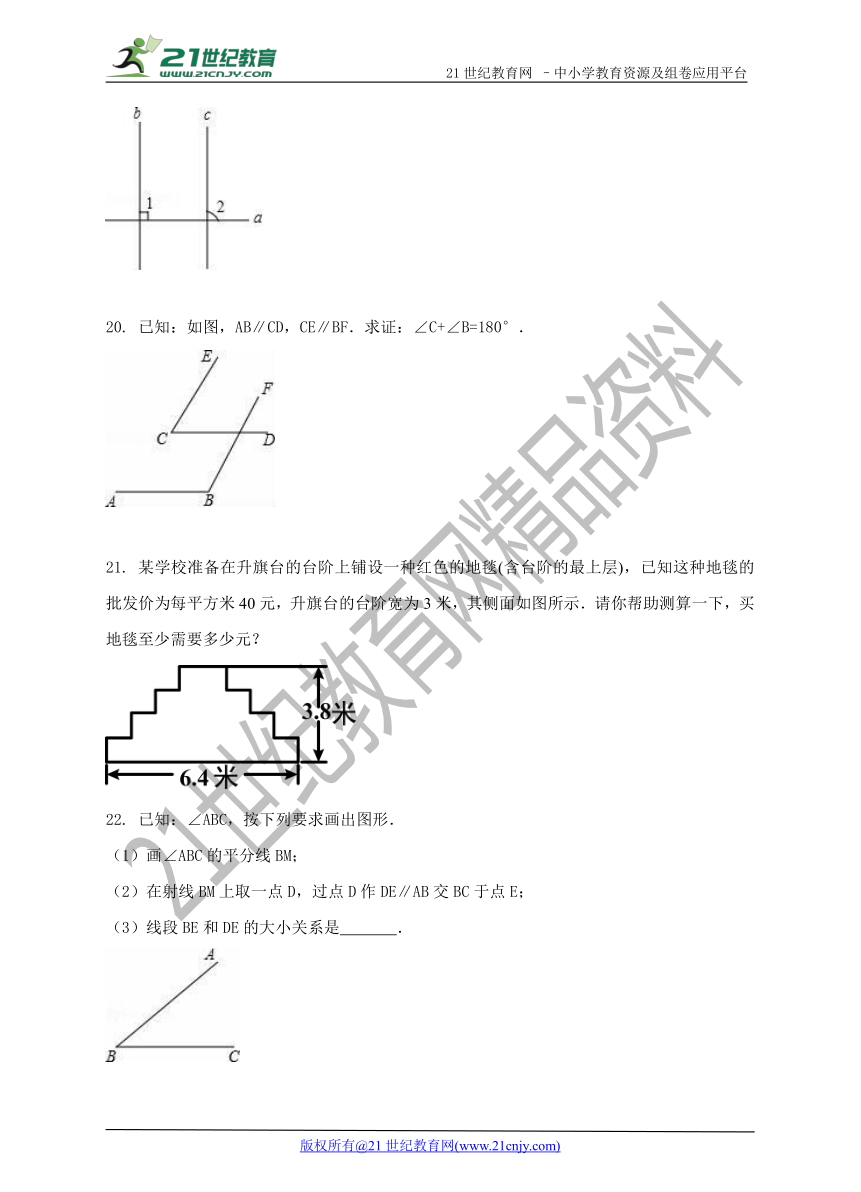
19. 证明填空:如图,已知直线b∥c,a⊥b
求证:a⊥c
证明:∵a⊥b(已知)
∴∠1=90°( )
又b∥c( )
∴∠1=∠2( )
∴∠2=∠1=90°( )
∴a⊥c( )
20. 已知:如图,AB∥CD,CE∥BF.求证:∠C+∠B=180°.
21. 某学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶的最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图所示.请你帮助测算一下,买地毯至少需要多少元?
22. 已知:∠ABC,按下列要求画出图形.
(1)画∠ABC的平分线BM;
(2)在射线BM上取一点D,过点D作DE∥AB交BC于点E;
(3)线段BE和DE的大小关系是 .
23. 如图,(1)已知AB∥CD,EF∥MN,∠1=110°,求∠2和∠4的度数;
(2)观察∠1与∠2,∠1与∠4边之间的关系,请你根据(1)的结果进行归纳.试着用文字表述这一规律;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.
24. 已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点.
(1)如图1,当点P在线段AB上(不与A、B两点重合)运动时,∠1、∠2、∠3之间有怎样的大小关系?请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠1、∠2、∠3之间的大小关系为 ;
(3)如图3,当点P在线段BA的延长线上运动时,∠1、∠2、∠3之间的大小关系为 .
参考答案:
一、选择题(本大题共10小题)
1. C
分析:距离是长度;在同一平面内,过不在直线上的点,才有且只有一条直线和已知直线平行;与同一条直线垂直的两条直线平行.
解:A、两点之间的距离是两点间的线段的长度,故本选项错误;
B、在同一平面内,过不在直线上的点,有且只有一条直线和已知直线平行,故本选项错误;
C、同一平面内,过一点有且只有一条直线与已知直线垂直,正确;
D、在同一平面内与同一条直线垂直的两条直线互相平行,故本选项错误.故答案选C。
2. A
分析:先根据平行线的性质求出∠3的度数,再由补角的定义即可得出结论.
解:∵直线a∥b,∠1=108°,
∴∠1=∠3=108°.
∵∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣108°=72°.
故选A.
3. D
分析:根据平移的性质,对选项进行一一分析,排除错误答案.
解:①中是旋转运动,不是平移;
②是平移;
③中是旋转运动,不是平移;
④是平移.故选D.
4. C
分析:先根据平行线的性质,求得∠B的度数,再根据直角三角形的性质,求得∠2的度数.
解:∵直线a∥b,∠1=46°,
∴∠B=∠1=46°,
又∵AC⊥AB,
∴∠2=90°﹣∠B=44°.
故选C
5. D
分析:首先根据题意画出图形,由∠A的两边与∠B的两边互相平行,根据平行线的性质,即可求得∠B的度数.
解:如图1:∵∠A的两边与∠B的两边互相平行,
∴∠1=∠A,∠B=∠1,
∵∠A=20°,
∴∠B=∠A=20°;
如图2:∵∠A的两边与∠B的两边互相平行,
∴∠1=∠A,∠1+∠B=180°,
∴∠B=180°﹣∠A=160°.
故选D.
6. D
分析:根据同位角的定义进行分析解答。
解:因为不知道直线AB和CD是否平行,平行时同位角相等,不平行时同位角不相等,所以无法确定同位角的大小关系,故选D.
7. A
分析:两次拐弯后,行驶方向与原来相同,说明两次拐弯后的方向是平行的.对题中的四个选项提供的条件,运用平行线的判定进行判断,能判定两直线平行者即为正确答案.
解:如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选A.
8. D
分析:根据平行线的性质进行判断即可.
解:因为l1∥l2,
所以∠1=(180°﹣∠2)+∠3,
可得:∠1+∠2﹣∠3=180°,
故选D
9. C
分析:根据题意做辅助线可作EF//AB,利用平行线的性质可解答.
解:如图,过点E向右作EF∥CD,则∠FED=∠γ;由AB∥CD,可知EF∥AB,所以∠α+∠AEF=180°,即∠AEF=180°-∠α.不难看出∠β=∠FED+∠AEF,由此得到∠β=∠γ+∠AEF=∠γ+180°-∠α,即
∠α+∠β-∠γ=180°,故选C.
10. D
分析:平行线的性质,平角定义,对顶角的性质,三角形内角和定理。
解:∵,∴∠ABn=。∴∠ABC=600。
又∵∠ACB=,∠A=450,
∴根据三角形内角和定理,得=1800-600-450=750。故选D。
二、填空题(本大题共8小题)
11. 分析:延长BC与a相交,先求出所得内错角的度数,再根据三角形外角性质即可求出.
解:如图,延长BC与a相交,
∵a∥b,∴∠1=∠50°;
∴∠ACB=∠1+28°=50°+28°=78°,
故应填78.
12. 分析:利用平移法求面积
解:根据平移的法则可得:草地的面积=(12-2)×6=60(平方厘米).
13. 分析:利用平行线的性质和翻折变换的性质即可求得.
解:∵∠ABC=120°,纸条的上下对边是平行的,
∴∠BCD=∠ABC=120°;
∵是折叠得到的∠1,
∴∠1=0.5×120°=60°.
故答案为:60°.
14.分析:先由AB∥CD,可得∠1+∠BEF=180°,而∠1=50°,易求∠BEF,而EG是∠BEF的角平分线,从而可求∠BEG,又AB∥CD,可知∠2=∠BEG,即可求∠2.
解:∵AB∥CD,
∴∠1+∠BEF=180°,
又∵∠1=50°,
∴∠BEF=130°,
又∵EG平分∠BEF,
∴∠FEG=∠BEG=65°,
∵AB∥CD,
∴∠2=∠BEG=65°.
故答案为:65°.
15.分析:根据平移的基本性质,得出四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC即可得出答案.
解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
16. 分析:根据对顶角及其平角的定义综合解答即可.
解:∵∠1=∠BOF,
∴∠3=∠AOC,∴∠1+∠2+∠3=180°
故答案为:180°.
17. 分析:利用平行线间的距离进行解答即可。
解:因为DE⊥AB,所以B与CD两平行线间距离是1.5cm, 则点C到AB的距离是1.5cm。
18.分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,
∴∠1=∠PAB.
又∵AB∥CD,
PE∥CD,
∴∠2=∠PCD,
∴∠1+∠2=∠PAB+∠PCD,
而∠APC=∠1+∠2,
∴∠APC=∠PAB+∠PCD.
故答案为:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
三、计算题(本大题共6小题)
19.分析:首先根据垂直定义可得∠1=90°,再根据平行线的性质可得∠2=∠1=90°,进而得到a⊥c.
证明:∵a⊥b(已知)
∴∠1=90°(垂直的定义 )
又b∥c(已知 )
∴∠1=∠2(两直线平行,同位角相等 )
∴∠2=∠1=90°(等量代换 )
∴a⊥c(垂直的定义 ),
故答案为:垂直的定义,已知,两直线平行,同位角相等,等量代换,垂直的定义.
20. 分析:根据两直线平行,内错角相等可得∠C=∠CDB,再根据两直线平行,同旁内角互补证明.
证明:∵AB∥CD,CE∥BF,
∴∠CDB+∠B=180°,
∠C=∠CDB,
∴∠C+∠B=180°.
21. 解:如图,平移线段,构成一个矩形,长,宽分别为6.4米,3.8米,
所以地毯的长度为6.4+3.8+3.8=14(米),地毯的面积为14×3=42(平方米),
所以买地毯至少需要42×40=1680(元).
答:买地毯至少需要1680元.
22. 分析:(1)根据角平分线的做法画出∠ABC的平分线BM;
(2)根据同位角相等,两直线平行画∠DEC=∠ABC,交BC于点E;
(3)根据平行线的性质以及角平分线定义得出∠BDE=∠DBE,再根据等角对等边即可得到BE=DE.
解:(1)(2)如图所示;
(3)如图,BE=DE,理由如下:
∵BM平分∠ABC,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE;
∴∠BDE=∠DBE,
∴BE=DE.
故答案为BE=DE.
23. 分析:(1)根据两直线平行同位角相等、两直线平行同旁内角互补即可解决问题.
(2)通过观察利用(1)的结果可以得到解决.
(3)利用(2)的结论这两个角互补,设未知数列出方程解决.
解:(1)解:∵AB∥CD,
∴∠1=∠2,
∵EF∥MN,
∴∠2+∠4=180°,
∵∠1=110°,
∴∠2=110°,∠4=70°.
(2)观察发现∠1=∠2,∠1+∠=180°,
规律:如果两个角的两边分别平行那么这两个角相等或互补.
(3)设这两个角分别为x,2x.
由结论(2)可知这两个角互补,x+2x=180°,解得x=60°,
所以这两个角分别为60°和120°.
24.分析:(1)过点P作a的平行线,根据平行线的性质进行解题;
(2)过点P作b的平行线PE,由平行线的性质可得出a∥b∥PE,由此即可得出结论;
(3)设直线AC与DP交于点F,由三角形外角的性质可得出∠1+∠3=∠PFA,再由平行线的性质即可得出结论.
解:(1)如图1,过点P作PE∥a,则∠1=∠CPE.
∵a∥b,PE∥a,
∴PE∥b,
∴∠2=∠DPE,
∴∠3=∠1+∠2;
(2)如图2,过点P作PE∥b,则∠2=∠EPD,
∵直线a∥b,
∴a∥PE,
∴∠1=∠3+∠EPD,即∠1=∠2+∠3.
故答案为:∠1=∠2+∠3;
(3)如图3,设直线AC与DP交于点F,
∵∠PFA是△PCF的外角,
∴∠PFA=∠1+∠3,
∵a∥b,
∴∠2=∠PFA,即∠2=∠1+∠3.
故答案为:∠2=∠1+∠3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
沪科版七年级下册数学第十章平行线、相交线与平移单元检测试题
一、选择题(本大题共10小题)
1. 下列说法正确的是( )
A.两点之间的距离是两点间的线段
B.同一平面内,过一点有且只有一条直线与已知直线平行
C.与同一条直线垂直的两条直线也垂直
D.同一平面内,过一点有且只有一条直线与已知直线垂直
2. a,b,c是同一平面内任意三条直线,交点可能有( )
A.1个或2个或3个 B.0个或1个或2个或3个
C.1个或2个 D.都不对
3.在以下现象中,属于平移的是( )
①在挡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动.
A.①② B.①③ C.②③ D.②④
4. 已知:如图,直线a∥b,AC⊥AB于A,AC交直线b于点C,∠1=46°,则∠2的度数是( )
A.50° B.45° C.44° D.30°
5. 已知∠A的两边与∠B的两边互相平行,且∠A=20°,则∠B的度数为( )
A.20° B.80° C.160° D.20°或160°
6. 如图,有三条公路,其中AC与AB垂直,小明和小亮分别从A,B两点沿AC,BC同时出发骑车到C城,若他们同时到达,则下列判断中正确的是( )
A.小亮骑车的速度快
B.小明骑车的速度快
C.两人骑车的速度一样快
D.因为不知道公路的长度,所以无法判断他们骑车速度的快慢
7. 某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯角度可能是( )
A.第一次左拐30°,第二次右拐30° B.第一次右拐50°,第二次左拐130°
C.第一次右拐50°,第二次右拐130° D.第一次左拐50°,第二次左拐120°
8. 如图,直线l1∥l2,则下列式子成立的是( )
A.∠1+∠2+∠3=180° B.∠1﹣∠2+∠3=180°
C.∠2+∠3﹣∠1=180° D.∠1+∠2﹣∠3=180°
9. 如图,如果AB ∥CD ,则∠α,∠β,∠γ之间的关系是 ( )
A. ∠α+∠β+∠γ=180° B. ∠α-∠β+∠γ=180°
C.∠α+∠β-∠γ=180° D.∠α+∠β+∠γ=270°
10. 小明同学把一个含有450角的直角三角板在如图所示的两条平行线上,测得,则的度数是( )
A.450 B.550 C.650 D.750
二、填空题(本大题共8小题)
11. 如图,直线a∥b,则∠ACB= 度.
12.如图在一块长为12cm,宽为6cm的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2cm)则空白部分表示的草地面积是 。
13. 如图,一张宽度相等的纸条,折叠后,若∠ABC=120°,则∠1的度数为 .
14. 如图,已知AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=50°,则∠2的度数为 .
15.如图,将周长为8的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为 。
16. 如图,直线CD、EF相交于点O,则∠1+∠2+∠3的度数是 度.
17. 如图,DE⊥AB于点E,经测量AD=BC=1.8 cm,DE=1.5 cm.,AB与CD两平行线间距离是 .点C到AB的距离是 .
18. 已知,如图,AB∥CD,分别探讨下面四个图形中∠APC与∠PAB,∠PCD之间的关系(温馨提示:添加适当辅助线)
(1)在图1中,∠APC与∠PAB,∠PCD之间的关系是: .
(2)在图2中,∠APC与∠PAB,∠PCD之间的关系是: .
(3)在图3中,∠APC与∠PAB,∠PCD之间的关系是: .
(4)在图4中,∠APC与∠PAB,∠PCD之间的关系是: .
三、计算题(本大题共6小题)
19. 证明填空:如图,已知直线b∥c,a⊥b
求证:a⊥c
证明:∵a⊥b(已知)
∴∠1=90°( )
又b∥c( )
∴∠1=∠2( )
∴∠2=∠1=90°( )
∴a⊥c( )
20. 已知:如图,AB∥CD,CE∥BF.求证:∠C+∠B=180°.
21. 某学校准备在升旗台的台阶上铺设一种红色的地毯(含台阶的最上层),已知这种地毯的批发价为每平方米40元,升旗台的台阶宽为3米,其侧面如图所示.请你帮助测算一下,买地毯至少需要多少元?
22. 已知:∠ABC,按下列要求画出图形.
(1)画∠ABC的平分线BM;
(2)在射线BM上取一点D,过点D作DE∥AB交BC于点E;
(3)线段BE和DE的大小关系是 .
23. 如图,(1)已知AB∥CD,EF∥MN,∠1=110°,求∠2和∠4的度数;
(2)观察∠1与∠2,∠1与∠4边之间的关系,请你根据(1)的结果进行归纳.试着用文字表述这一规律;
(3)利用(2)的结论解答:如果两个角的两边分别平行,其中一角是另一个角的两倍,求这两个角的大小.
24. 已知:如图,直线a∥b,直线c与直线a、b分别相交于C、D两点,直线d与直线a、b分别相交于A、B两点.
(1)如图1,当点P在线段AB上(不与A、B两点重合)运动时,∠1、∠2、∠3之间有怎样的大小关系?请说明理由;
(2)如图2,当点P在线段AB的延长线上运动时,∠1、∠2、∠3之间的大小关系为 ;
(3)如图3,当点P在线段BA的延长线上运动时,∠1、∠2、∠3之间的大小关系为 .
参考答案:
一、选择题(本大题共10小题)
1. C
分析:距离是长度;在同一平面内,过不在直线上的点,才有且只有一条直线和已知直线平行;与同一条直线垂直的两条直线平行.
解:A、两点之间的距离是两点间的线段的长度,故本选项错误;
B、在同一平面内,过不在直线上的点,有且只有一条直线和已知直线平行,故本选项错误;
C、同一平面内,过一点有且只有一条直线与已知直线垂直,正确;
D、在同一平面内与同一条直线垂直的两条直线互相平行,故本选项错误.故答案选C。
2. A
分析:先根据平行线的性质求出∠3的度数,再由补角的定义即可得出结论.
解:∵直线a∥b,∠1=108°,
∴∠1=∠3=108°.
∵∠2+∠3=180°,
∴∠2=180°﹣∠3=180°﹣108°=72°.
故选A.
3. D
分析:根据平移的性质,对选项进行一一分析,排除错误答案.
解:①中是旋转运动,不是平移;
②是平移;
③中是旋转运动,不是平移;
④是平移.故选D.
4. C
分析:先根据平行线的性质,求得∠B的度数,再根据直角三角形的性质,求得∠2的度数.
解:∵直线a∥b,∠1=46°,
∴∠B=∠1=46°,
又∵AC⊥AB,
∴∠2=90°﹣∠B=44°.
故选C
5. D
分析:首先根据题意画出图形,由∠A的两边与∠B的两边互相平行,根据平行线的性质,即可求得∠B的度数.
解:如图1:∵∠A的两边与∠B的两边互相平行,
∴∠1=∠A,∠B=∠1,
∵∠A=20°,
∴∠B=∠A=20°;
如图2:∵∠A的两边与∠B的两边互相平行,
∴∠1=∠A,∠1+∠B=180°,
∴∠B=180°﹣∠A=160°.
故选D.
6. D
分析:根据同位角的定义进行分析解答。
解:因为不知道直线AB和CD是否平行,平行时同位角相等,不平行时同位角不相等,所以无法确定同位角的大小关系,故选D.
7. A
分析:两次拐弯后,行驶方向与原来相同,说明两次拐弯后的方向是平行的.对题中的四个选项提供的条件,运用平行线的判定进行判断,能判定两直线平行者即为正确答案.
解:如图所示(实线为行驶路线):
A符合“同位角相等,两直线平行”的判定,其余均不符合平行线的判定.
故选A.
8. D
分析:根据平行线的性质进行判断即可.
解:因为l1∥l2,
所以∠1=(180°﹣∠2)+∠3,
可得:∠1+∠2﹣∠3=180°,
故选D
9. C
分析:根据题意做辅助线可作EF//AB,利用平行线的性质可解答.
解:如图,过点E向右作EF∥CD,则∠FED=∠γ;由AB∥CD,可知EF∥AB,所以∠α+∠AEF=180°,即∠AEF=180°-∠α.不难看出∠β=∠FED+∠AEF,由此得到∠β=∠γ+∠AEF=∠γ+180°-∠α,即
∠α+∠β-∠γ=180°,故选C.
10. D
分析:平行线的性质,平角定义,对顶角的性质,三角形内角和定理。
解:∵,∴∠ABn=。∴∠ABC=600。
又∵∠ACB=,∠A=450,
∴根据三角形内角和定理,得=1800-600-450=750。故选D。
二、填空题(本大题共8小题)
11. 分析:延长BC与a相交,先求出所得内错角的度数,再根据三角形外角性质即可求出.
解:如图,延长BC与a相交,
∵a∥b,∴∠1=∠50°;
∴∠ACB=∠1+28°=50°+28°=78°,
故应填78.
12. 分析:利用平移法求面积
解:根据平移的法则可得:草地的面积=(12-2)×6=60(平方厘米).
13. 分析:利用平行线的性质和翻折变换的性质即可求得.
解:∵∠ABC=120°,纸条的上下对边是平行的,
∴∠BCD=∠ABC=120°;
∵是折叠得到的∠1,
∴∠1=0.5×120°=60°.
故答案为:60°.
14.分析:先由AB∥CD,可得∠1+∠BEF=180°,而∠1=50°,易求∠BEF,而EG是∠BEF的角平分线,从而可求∠BEG,又AB∥CD,可知∠2=∠BEG,即可求∠2.
解:∵AB∥CD,
∴∠1+∠BEF=180°,
又∵∠1=50°,
∴∠BEF=130°,
又∵EG平分∠BEF,
∴∠FEG=∠BEG=65°,
∵AB∥CD,
∴∠2=∠BEG=65°.
故答案为:65°.
15.分析:根据平移的基本性质,得出四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC即可得出答案.
解:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
16. 分析:根据对顶角及其平角的定义综合解答即可.
解:∵∠1=∠BOF,
∴∠3=∠AOC,∴∠1+∠2+∠3=180°
故答案为:180°.
17. 分析:利用平行线间的距离进行解答即可。
解:因为DE⊥AB,所以B与CD两平行线间距离是1.5cm, 则点C到AB的距离是1.5cm。
18.分析:(1)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,同旁内角互补,即可求得答案;
(2)首先过点P作PE∥AB,由AB∥CD,即可得AB∥PE∥CD,然后根据两直线平行,内错角相等,即可求得答案;
(3)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案;
(4)由AB∥CD,根据两直线平行,同位角线相等,以及三角形外角的性质,即可求得答案.
解:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
(5)在图2中,求证:∠APC=∠PAB+∠PCD.
证明:过P点作PE∥AB,
∴∠1=∠PAB.
又∵AB∥CD,
PE∥CD,
∴∠2=∠PCD,
∴∠1+∠2=∠PAB+∠PCD,
而∠APC=∠1+∠2,
∴∠APC=∠PAB+∠PCD.
故答案为:(1)∠APC+∠PAB+∠PCD=360°;
(2)∠APC=∠PAB+∠PCD;
(3)∠PAB=∠APC+∠PCD;
(4)∠PCD=∠APC+∠PAB.
三、计算题(本大题共6小题)
19.分析:首先根据垂直定义可得∠1=90°,再根据平行线的性质可得∠2=∠1=90°,进而得到a⊥c.
证明:∵a⊥b(已知)
∴∠1=90°(垂直的定义 )
又b∥c(已知 )
∴∠1=∠2(两直线平行,同位角相等 )
∴∠2=∠1=90°(等量代换 )
∴a⊥c(垂直的定义 ),
故答案为:垂直的定义,已知,两直线平行,同位角相等,等量代换,垂直的定义.
20. 分析:根据两直线平行,内错角相等可得∠C=∠CDB,再根据两直线平行,同旁内角互补证明.
证明:∵AB∥CD,CE∥BF,
∴∠CDB+∠B=180°,
∠C=∠CDB,
∴∠C+∠B=180°.
21. 解:如图,平移线段,构成一个矩形,长,宽分别为6.4米,3.8米,
所以地毯的长度为6.4+3.8+3.8=14(米),地毯的面积为14×3=42(平方米),
所以买地毯至少需要42×40=1680(元).
答:买地毯至少需要1680元.
22. 分析:(1)根据角平分线的做法画出∠ABC的平分线BM;
(2)根据同位角相等,两直线平行画∠DEC=∠ABC,交BC于点E;
(3)根据平行线的性质以及角平分线定义得出∠BDE=∠DBE,再根据等角对等边即可得到BE=DE.
解:(1)(2)如图所示;
(3)如图,BE=DE,理由如下:
∵BM平分∠ABC,
∴∠ABD=∠DBE,
∵DE∥AB,
∴∠ABD=∠BDE;
∴∠BDE=∠DBE,
∴BE=DE.
故答案为BE=DE.
23. 分析:(1)根据两直线平行同位角相等、两直线平行同旁内角互补即可解决问题.
(2)通过观察利用(1)的结果可以得到解决.
(3)利用(2)的结论这两个角互补,设未知数列出方程解决.
解:(1)解:∵AB∥CD,
∴∠1=∠2,
∵EF∥MN,
∴∠2+∠4=180°,
∵∠1=110°,
∴∠2=110°,∠4=70°.
(2)观察发现∠1=∠2,∠1+∠=180°,
规律:如果两个角的两边分别平行那么这两个角相等或互补.
(3)设这两个角分别为x,2x.
由结论(2)可知这两个角互补,x+2x=180°,解得x=60°,
所以这两个角分别为60°和120°.
24.分析:(1)过点P作a的平行线,根据平行线的性质进行解题;
(2)过点P作b的平行线PE,由平行线的性质可得出a∥b∥PE,由此即可得出结论;
(3)设直线AC与DP交于点F,由三角形外角的性质可得出∠1+∠3=∠PFA,再由平行线的性质即可得出结论.
解:(1)如图1,过点P作PE∥a,则∠1=∠CPE.
∵a∥b,PE∥a,
∴PE∥b,
∴∠2=∠DPE,
∴∠3=∠1+∠2;
(2)如图2,过点P作PE∥b,则∠2=∠EPD,
∵直线a∥b,
∴a∥PE,
∴∠1=∠3+∠EPD,即∠1=∠2+∠3.
故答案为:∠1=∠2+∠3;
(3)如图3,设直线AC与DP交于点F,
∵∠PFA是△PCF的外角,
∴∠PFA=∠1+∠3,
∵a∥b,
∴∠2=∠PFA,即∠2=∠1+∠3.
故答案为:∠2=∠1+∠3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
