6.2方差同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
湘教版七年级下册数学6.2方差同步练习
一、选择题(本大题共8小题)
1. 下列特征量不能反映一组数据集中趋势的是( )
A.众数 B.中位数 C.方差 D.平均数
2. 已知一组数据:3,3,4,7,8,则它的方差为( ).
A、4.4 B、4.5 C、4.3 D、4.6
3. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为,,,,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4 B.2,3,2 C.3,2,0.4 D.3,3,2
5. 为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5, B.5,5,10 C.6,5.5, D.5,5,
6. 某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩及其方差S2如表所示:
甲 乙 丙 丁
(环) 8.4 8.6 8.6 7.6
S2 0.74 0.56 0.94 1.92
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
7. 在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
8. 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
二、填空题(本大题共6小题)
9. 已知一组数据为1,2,3,4,5,则这组数据的方差为 .
10. 若甲、乙、丙、丁四位同学一学期4次数学测试的平均成绩恰好都是85分,方差分别为S甲2=0.80,S乙2=1.31,S丙2=1.72,S丁2=0.42,则成绩最稳定的同学是 。
11. 甲乙两人在相同情况下各射靶10次,环数的方差分别是,,则射击稳定性高的是 .
12. 甲乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷)
经计算,甲=10,乙=10,试根据这组数据估计 种水稻品种的产量比较稳定。
13. 跳远运动员李刚对训练效果进行测试,6次跳远的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9.(单位:m)这六次成绩的平均数为7.8,方差为.如果李刚再跳两次,成绩分别为7.7,7.9.则李刚这8次跳远成绩的方差 (填“变大”、“不变”或“变小”).
14. 已知样本数据x1,x2,…xn的方差为4,则数据2x1+3,2x2+3,…2xn+3的方差是 .
三、计算题(本大题共4小题)
15. 为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据(单位:s)如下表:
编号类型 一 二 三 四 五 六 七 八 九 十
甲种电子钟 1 -3 -4 4 2 -2 2 -1 -1 2
乙种电子钟 4 -3 -1 2 -2 1 -2 2 -2 1
(1)计算甲、乙两种电子钟走时误差的平均数.
(2)计算甲、乙两种电子钟走时误差的方差.
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你会买哪种电子钟?为什么?
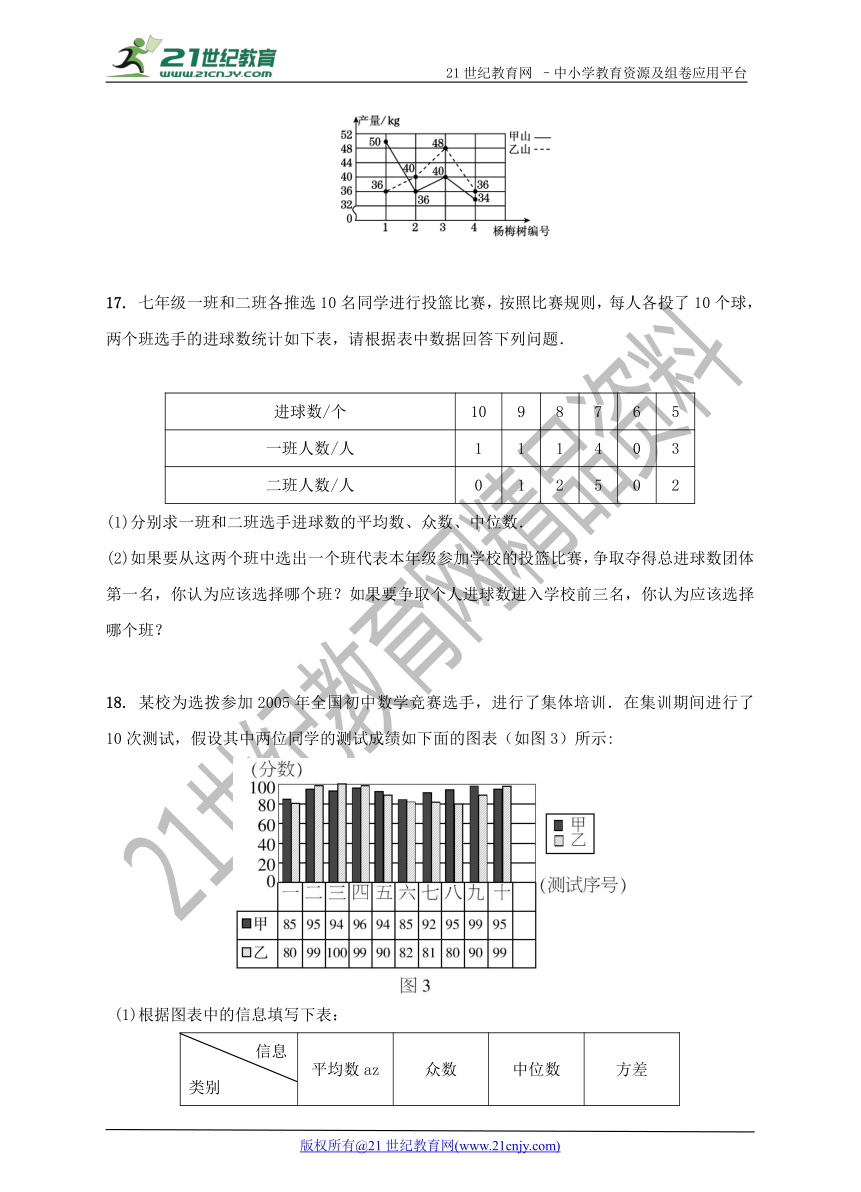
16. 王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率为98%,现已挂果,经济效益初步显现.为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵树的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算估计,哪个山上的杨梅产量较稳定.
17. 七年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答下列问题.
进球数/个 10 9 8 7 6 5
一班人数/人 1 1 1 4 0 3
二班人数/人 0 1 2 5 0 2
(1)分别求一班和二班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表本年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
18. 某校为选拨参加2005年全国初中数学竞赛选手,进行了集体培训.在集训期间进行了10次测试,假设其中两位同学的测试成绩如下面的图表(如图3)所示:
(1)根据图表中的信息填写下表:
信息类别 平均数az 众数 中位数 方差
甲 93 95 18.8
乙 90 90 68.8
(2)这两位同学的测试成绩各有什么特点(从不同的角度分别说出一条即可)?
(3)为了使参赛选手取得好成绩,应该选谁参加比赛?为什么?
参考答案:
一、选择题(本大题共8小题)
1. C
分析:根据中位数、众数、平均数和方差的意义进行判断.
解:数据的平均数、众数、中位数是描述一组数据集中趋势的特征量,极差、方差是衡量一组数据偏离其平均数的大小(即波动大小)的特征数.
故选C.
2. A
分析:根据平均数的计算公式先算出这组数据的平均数,再根据方差公式进行计算即可.
解:这组数据的平均数是:(3+3+4+7+8)÷5=5,
则这组数据的方差为: [(3﹣5)2+(3﹣5)2+(4﹣5)2+(7﹣5)2+(8﹣5)2]=4.4.
故答案为:4.4.故选A
3. D
分析:本题考查方差的意义:方差越大,数据的波动越大,说明数据分布比较分散;方差越小,数据的波动越小,说明数据分布比较集中,数据越稳定。
解:根据方差越小,数据波动越小,越稳定,可知丁的方差最小,最稳定。故选D。
4.A
分析:先根据平均数的定义求出x的值,再根据众数、中位数的定义和方差公式分别进行解答即可.
解:根据题意, =3,解得:x=3,
∴这组数据从小到大排列为:2,3,3,3,4;
则这组数据的中位数为3,
这组数据3出现的次数最多,出现了3次,故众数为3;
其方差是:×[(2﹣3)2+3×(3﹣3)2+(4﹣3)2]=0.4,
故选A.
5. D
分析:根据平均数,可得x的值,根据众数的定义、中位数的定义、方差的定义,可得答案.
解:由5,7,x,3,4,6.已知他们平均每人捐5本,得
x=5.
众数是5,中位数是5,
方差=,
故选:D.
6.B
分析:从平均成绩分析乙和丙要比甲和丁好,从方差分析甲和乙的成绩比丙和丁稳定,综合两个方面可选出乙.
解:根据平均成绩可得乙和丙要比甲和丁好,根据方差可得甲和乙的成绩比丙和丁稳定,
因此要选择一名成绩高且发挥稳定的学生参赛,因选择乙,
故选:B
7. C
分析:分别求出甲、乙的平均数、众数、中位数及方差可逐一判断.
解:A、==8, ==8,故此选项正确;
B、甲得分次数最多是8分,即众数为8分,乙得分最多的是9分,即众数为9分,故此选项正确;
C、∵甲得分从小到大排列为:7、8、8、8、9,∴甲的中位数是8分;
∵乙得分从小到大排列为:6、7、9、9、9,∴乙的中位数是9分;故此选项错误;
D、∵=×[(8﹣8)2+(7﹣8)2+(9﹣8)2+(8﹣8)2+(8﹣8)2]=×2=0.4,
=×[(7﹣8)2+(9﹣8)2+(6﹣8)2+(9﹣8)2+(9﹣8)2]=×8=1.6,
∴<,故D正确;
故选:C.
8.D
分析:根据方差的计算公式求出丁的成绩的方差,根据方差的性质解答即可.
解:由图可知丁射击10次的成绩为:8、8、9、7、8、8、9、7、8、8,
则丁的成绩的平均数为:×(8+8+9+7+8+8+9+7+8+8)=8,
丁的成绩的方差为:×[(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2]=0.4,
∵丁的成绩的方差最小,
∴丁的成绩最稳定,
∴参赛选手应选丁,
故选:D.
二、填空题(本大题共6小题)
9.分析:先求出这5个数的平均数,然后利用方差公式求解即可.
解:平均数为=(1+2+3+4+5)÷5=3,
S2= [(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
故答案为:2.
10. 分析:首先比较出S甲2,S乙2,S丙2,S丁2的大小关系,然后根据方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,判断出成绩最稳定的同学是谁即可.
解:∵S甲2=0.80,S乙2=1.31,S丙2=1.72,S丁2=0.42,
∴S丁2<S甲2<S乙2<S丙2,
∴成绩最稳定的同学是丁.
11. 分析:根据方差的意义判断.方差是反映数据波动大小的量,方差越小,越稳定.
解:∵S甲2<S乙2,
∴甲射击稳定程度高.
故选A.
12.分析:本题考查数据分析中的方差特性.一般情况下,在比较的数据平均数相等或近似相等时,方差值越大,波动就大,所反映该组数据不稳定(或不整齐或波动较大).
解:甲=10,乙=10,可以比较表中数据偏离平均数10(吨/公顷)比较大的是乙.
13.分析:根据平均数的定义先求出这组数据的平均数,再根据方差公式求出这组数据的方差,然后进行比较即可求出答案.
解:∵李刚再跳两次,成绩分别为7.7,7.9,
∴这组数据的平均数是=7.8,
∴这8次跳远成绩的方差是:
S2= [(7.6﹣7.8)2+(7.8﹣7.8)2+2×(7.7﹣7.8)2+(7.8﹣7.8)2+(8.0﹣7.8)2+2×(7.9﹣7.8)2]=,
,
∴方差变大;
故答案为:变大.
14.分析:首先设原数据的平均数为 ,则新数据的平均数为2+3,然后利用方差的公式计算得出答案,求出标准差即可.
解:设原数据的平均数为,则新数据的平均数为2 +3,
则其方差为 [(x1-)2+(x2-)2+…+(xn-)2]=4,
则新数据的方差为:[(2x1+3-2 -3)2+(2x2+3-2 -3)2+…+(2xn+3-2 -3)2]
=4×[(x1-)2+(x2-)2+…+(xn-)2]
=16.故答案是16.
三、计算题(本大题共4小题)
15. 解析:(1)甲种电子钟走时误差的平均数是:(1-3-4+4+2-2+2-1-1+2)=0,
乙种电子钟走时误差的平均数是:(4-3-1+2-2+1-2+2-2+1)=0.
(2)S2甲= [(1-0)2+(-3-0)2+…+(2-0)2]= ×60=6(s2),
S2乙= [(4-0)2+(-3-0)2+…+(1-0)2]= ×48=4.8(s2),
∴甲乙两种电子钟走时误差的方差分别是6s2和4.8s2;(3)我会买乙种电子钟,因为两种类型的电子钟价格相同,且甲的方差比乙的大,说明乙的稳定性更好,故乙种电子钟的质量更优.
16. 分析:(1)根据平均数的定义进行计算;(2)计算方差进行计算即可。
解:(1)(千克)
(千克)
总产量为(千克);
(2)(千克2)
(千克2)
∴
答:乙山上的杨梅产量较稳定。
17.分析:(1)利用平均数、中位数和众数的定义直接求出求出;
(2)根据方差和个人发挥的最好成绩进行选择.
解:(1)一班进球平均数:(10×1+9×1+8×1+7×4+6×0+5×3)=7(个),
二班进球平均数:(10×0+9×1+8×2+7×5+6×0+5×2)=7(个),
一班投中7个球的有4人,人数最多,故众数为7(个);
二班投中7个球的有5人,人数最多,故众数为7(个);
一班中位数:第五第六名同学进7个球,故中位数为7(个);
二班中位数:第五第六名同学进7个球,故中位数为7(个).
(2)一班的方差S12=[(10-7)2+(9-7)2+(8-7)2+4×(7-7)2+0×(6-7)2+3×(5-7)2]=2.6,
二班的方差S22=[0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+(6-7)2+2×(5-7)2]=1.4,
二班选手水平发挥更稳定,争取夺得总进球数团体第一名,应该选择二班;
一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班.
18. 分析:(1)对甲的数据由小到大进行整理,可得甲的中位数;可直接得到乙的众数;
(2)此题是开放题目,因此学生的回答是多样的,例如:甲考试成绩较稳定,因为方差,极差较小(或甲的平均数比乙的平均数高);乙有潜力,因为乙的最好成绩比甲的最好成绩高等;
(3)此题的选择也是不一的,例如:选甲,因为10次测验,甲有8次不少于90分,而乙仅有6次;选乙,因为乙有4次在99分以上.解:(1)甲的中位数==94.5,乙的众数是99;(2)从稳定性看:甲考试成绩较稳定,因为方差,极差较小;从平均数看:甲的平均数比乙的平均数高;乙有潜力,因为乙的最好成绩比甲的最好成绩高.从众数看:乙的成绩比甲好.从中位数看:甲比乙的成绩好.(3)10次测验,甲有8次不少于90分,而乙仅有6次,若想获奖可能性较大,可选甲参赛;
若想拿到更好的名次可选乙,因为乙有4次在99分以上.
参考答案:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
湘教版七年级下册数学6.2方差同步练习
一、选择题(本大题共8小题)
1. 下列特征量不能反映一组数据集中趋势的是( )
A.众数 B.中位数 C.方差 D.平均数
2. 已知一组数据:3,3,4,7,8,则它的方差为( ).
A、4.4 B、4.5 C、4.3 D、4.6
3. 甲、乙、丙、丁四人进行射击测试,每人10次射击成绩的平均数都为8.8环,方差分别为,,,,则四人中成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
4. 一组数据2,x,4,3,3的平均数是3,则这组数据的中位数、众数、方差分别是( )
A.3,3,0.4 B.2,3,2 C.3,2,0.4 D.3,3,2
5. 为了响应学校“书香校园”建设,阳光班的同学们积极捐书,其中宏志学习小组的同学捐书册数分别是:5,7,x,3,4,6.已知他们平均每人捐5本,则这组数据的众数、中位数和方差分别是( )
A.5,5, B.5,5,10 C.6,5.5, D.5,5,
6. 某体校要从四名射击选手中选拔一名参加省体育运动会,选拔赛中每名选手连续射靶10次,他们各自的平均成绩及其方差S2如表所示:
甲 乙 丙 丁
(环) 8.4 8.6 8.6 7.6
S2 0.74 0.56 0.94 1.92
如果要选出一名成绩高且发挥稳定的选手参赛,则应选择的选手是( )
A.甲 B.乙 C.丙 D.丁
7. 在“爱我永州”中学生演讲比赛中,五位评委分别给甲、乙两位选手的评分如下:
甲:8、7、9、8、8
乙:7、9、6、9、9
则下列说法中错误的是( )
A.甲、乙得分的平均数都是8
B.甲得分的众数是8,乙得分的众数是9
C.甲得分的中位数是9,乙得分的中位数是6
D.甲得分的方差比乙得分的方差小
8. 某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
二、填空题(本大题共6小题)
9. 已知一组数据为1,2,3,4,5,则这组数据的方差为 .
10. 若甲、乙、丙、丁四位同学一学期4次数学测试的平均成绩恰好都是85分,方差分别为S甲2=0.80,S乙2=1.31,S丙2=1.72,S丁2=0.42,则成绩最稳定的同学是 。
11. 甲乙两人在相同情况下各射靶10次,环数的方差分别是,,则射击稳定性高的是 .
12. 甲乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷)
经计算,甲=10,乙=10,试根据这组数据估计 种水稻品种的产量比较稳定。
13. 跳远运动员李刚对训练效果进行测试,6次跳远的成绩如下:7.6,7.8,7.7,7.8,8.0,7.9.(单位:m)这六次成绩的平均数为7.8,方差为.如果李刚再跳两次,成绩分别为7.7,7.9.则李刚这8次跳远成绩的方差 (填“变大”、“不变”或“变小”).
14. 已知样本数据x1,x2,…xn的方差为4,则数据2x1+3,2x2+3,…2xn+3的方差是 .
三、计算题(本大题共4小题)
15. 为了比较市场上甲、乙两种电子钟每日走时误差的情况,从这两种电子钟中,各随机抽取10台进行测试,两种电子钟走时误差的数据(单位:s)如下表:
编号类型 一 二 三 四 五 六 七 八 九 十
甲种电子钟 1 -3 -4 4 2 -2 2 -1 -1 2
乙种电子钟 4 -3 -1 2 -2 1 -2 2 -2 1
(1)计算甲、乙两种电子钟走时误差的平均数.
(2)计算甲、乙两种电子钟走时误差的方差.
(3)根据经验,走时稳定性较好的电子钟质量更优.若两种类型的电子钟价格相同,请问:你会买哪种电子钟?为什么?
16. 王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活率为98%,现已挂果,经济效益初步显现.为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵树的产量如折线统计图所示.
(1)分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;
(2)试通过计算估计,哪个山上的杨梅产量较稳定.
17. 七年级一班和二班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球,两个班选手的进球数统计如下表,请根据表中数据回答下列问题.
进球数/个 10 9 8 7 6 5
一班人数/人 1 1 1 4 0 3
二班人数/人 0 1 2 5 0 2
(1)分别求一班和二班选手进球数的平均数、众数、中位数.
(2)如果要从这两个班中选出一个班代表本年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班?如果要争取个人进球数进入学校前三名,你认为应该选择哪个班?
18. 某校为选拨参加2005年全国初中数学竞赛选手,进行了集体培训.在集训期间进行了10次测试,假设其中两位同学的测试成绩如下面的图表(如图3)所示:
(1)根据图表中的信息填写下表:
信息类别 平均数az 众数 中位数 方差
甲 93 95 18.8
乙 90 90 68.8
(2)这两位同学的测试成绩各有什么特点(从不同的角度分别说出一条即可)?
(3)为了使参赛选手取得好成绩,应该选谁参加比赛?为什么?
参考答案:
一、选择题(本大题共8小题)
1. C
分析:根据中位数、众数、平均数和方差的意义进行判断.
解:数据的平均数、众数、中位数是描述一组数据集中趋势的特征量,极差、方差是衡量一组数据偏离其平均数的大小(即波动大小)的特征数.
故选C.
2. A
分析:根据平均数的计算公式先算出这组数据的平均数,再根据方差公式进行计算即可.
解:这组数据的平均数是:(3+3+4+7+8)÷5=5,
则这组数据的方差为: [(3﹣5)2+(3﹣5)2+(4﹣5)2+(7﹣5)2+(8﹣5)2]=4.4.
故答案为:4.4.故选A
3. D
分析:本题考查方差的意义:方差越大,数据的波动越大,说明数据分布比较分散;方差越小,数据的波动越小,说明数据分布比较集中,数据越稳定。
解:根据方差越小,数据波动越小,越稳定,可知丁的方差最小,最稳定。故选D。
4.A
分析:先根据平均数的定义求出x的值,再根据众数、中位数的定义和方差公式分别进行解答即可.
解:根据题意, =3,解得:x=3,
∴这组数据从小到大排列为:2,3,3,3,4;
则这组数据的中位数为3,
这组数据3出现的次数最多,出现了3次,故众数为3;
其方差是:×[(2﹣3)2+3×(3﹣3)2+(4﹣3)2]=0.4,
故选A.
5. D
分析:根据平均数,可得x的值,根据众数的定义、中位数的定义、方差的定义,可得答案.
解:由5,7,x,3,4,6.已知他们平均每人捐5本,得
x=5.
众数是5,中位数是5,
方差=,
故选:D.
6.B
分析:从平均成绩分析乙和丙要比甲和丁好,从方差分析甲和乙的成绩比丙和丁稳定,综合两个方面可选出乙.
解:根据平均成绩可得乙和丙要比甲和丁好,根据方差可得甲和乙的成绩比丙和丁稳定,
因此要选择一名成绩高且发挥稳定的学生参赛,因选择乙,
故选:B
7. C
分析:分别求出甲、乙的平均数、众数、中位数及方差可逐一判断.
解:A、==8, ==8,故此选项正确;
B、甲得分次数最多是8分,即众数为8分,乙得分最多的是9分,即众数为9分,故此选项正确;
C、∵甲得分从小到大排列为:7、8、8、8、9,∴甲的中位数是8分;
∵乙得分从小到大排列为:6、7、9、9、9,∴乙的中位数是9分;故此选项错误;
D、∵=×[(8﹣8)2+(7﹣8)2+(9﹣8)2+(8﹣8)2+(8﹣8)2]=×2=0.4,
=×[(7﹣8)2+(9﹣8)2+(6﹣8)2+(9﹣8)2+(9﹣8)2]=×8=1.6,
∴<,故D正确;
故选:C.
8.D
分析:根据方差的计算公式求出丁的成绩的方差,根据方差的性质解答即可.
解:由图可知丁射击10次的成绩为:8、8、9、7、8、8、9、7、8、8,
则丁的成绩的平均数为:×(8+8+9+7+8+8+9+7+8+8)=8,
丁的成绩的方差为:×[(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2]=0.4,
∵丁的成绩的方差最小,
∴丁的成绩最稳定,
∴参赛选手应选丁,
故选:D.
二、填空题(本大题共6小题)
9.分析:先求出这5个数的平均数,然后利用方差公式求解即可.
解:平均数为=(1+2+3+4+5)÷5=3,
S2= [(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
故答案为:2.
10. 分析:首先比较出S甲2,S乙2,S丙2,S丁2的大小关系,然后根据方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好,判断出成绩最稳定的同学是谁即可.
解:∵S甲2=0.80,S乙2=1.31,S丙2=1.72,S丁2=0.42,
∴S丁2<S甲2<S乙2<S丙2,
∴成绩最稳定的同学是丁.
11. 分析:根据方差的意义判断.方差是反映数据波动大小的量,方差越小,越稳定.
解:∵S甲2<S乙2,
∴甲射击稳定程度高.
故选A.
12.分析:本题考查数据分析中的方差特性.一般情况下,在比较的数据平均数相等或近似相等时,方差值越大,波动就大,所反映该组数据不稳定(或不整齐或波动较大).
解:甲=10,乙=10,可以比较表中数据偏离平均数10(吨/公顷)比较大的是乙.
13.分析:根据平均数的定义先求出这组数据的平均数,再根据方差公式求出这组数据的方差,然后进行比较即可求出答案.
解:∵李刚再跳两次,成绩分别为7.7,7.9,
∴这组数据的平均数是=7.8,
∴这8次跳远成绩的方差是:
S2= [(7.6﹣7.8)2+(7.8﹣7.8)2+2×(7.7﹣7.8)2+(7.8﹣7.8)2+(8.0﹣7.8)2+2×(7.9﹣7.8)2]=,
,
∴方差变大;
故答案为:变大.
14.分析:首先设原数据的平均数为 ,则新数据的平均数为2+3,然后利用方差的公式计算得出答案,求出标准差即可.
解:设原数据的平均数为,则新数据的平均数为2 +3,
则其方差为 [(x1-)2+(x2-)2+…+(xn-)2]=4,
则新数据的方差为:[(2x1+3-2 -3)2+(2x2+3-2 -3)2+…+(2xn+3-2 -3)2]
=4×[(x1-)2+(x2-)2+…+(xn-)2]
=16.故答案是16.
三、计算题(本大题共4小题)
15. 解析:(1)甲种电子钟走时误差的平均数是:(1-3-4+4+2-2+2-1-1+2)=0,
乙种电子钟走时误差的平均数是:(4-3-1+2-2+1-2+2-2+1)=0.
(2)S2甲= [(1-0)2+(-3-0)2+…+(2-0)2]= ×60=6(s2),
S2乙= [(4-0)2+(-3-0)2+…+(1-0)2]= ×48=4.8(s2),
∴甲乙两种电子钟走时误差的方差分别是6s2和4.8s2;(3)我会买乙种电子钟,因为两种类型的电子钟价格相同,且甲的方差比乙的大,说明乙的稳定性更好,故乙种电子钟的质量更优.
16. 分析:(1)根据平均数的定义进行计算;(2)计算方差进行计算即可。
解:(1)(千克)
(千克)
总产量为(千克);
(2)(千克2)
(千克2)
∴
答:乙山上的杨梅产量较稳定。
17.分析:(1)利用平均数、中位数和众数的定义直接求出求出;
(2)根据方差和个人发挥的最好成绩进行选择.
解:(1)一班进球平均数:(10×1+9×1+8×1+7×4+6×0+5×3)=7(个),
二班进球平均数:(10×0+9×1+8×2+7×5+6×0+5×2)=7(个),
一班投中7个球的有4人,人数最多,故众数为7(个);
二班投中7个球的有5人,人数最多,故众数为7(个);
一班中位数:第五第六名同学进7个球,故中位数为7(个);
二班中位数:第五第六名同学进7个球,故中位数为7(个).
(2)一班的方差S12=[(10-7)2+(9-7)2+(8-7)2+4×(7-7)2+0×(6-7)2+3×(5-7)2]=2.6,
二班的方差S22=[0×(10-7)2+(9-7)2+2×(8-7)2+5×(7-7)2+(6-7)2+2×(5-7)2]=1.4,
二班选手水平发挥更稳定,争取夺得总进球数团体第一名,应该选择二班;
一班前三名选手的成绩突出,分别进10个、9个、8个球,如果要争取个人进球数进入学校前三名,应该选择一班.
18. 分析:(1)对甲的数据由小到大进行整理,可得甲的中位数;可直接得到乙的众数;
(2)此题是开放题目,因此学生的回答是多样的,例如:甲考试成绩较稳定,因为方差,极差较小(或甲的平均数比乙的平均数高);乙有潜力,因为乙的最好成绩比甲的最好成绩高等;
(3)此题的选择也是不一的,例如:选甲,因为10次测验,甲有8次不少于90分,而乙仅有6次;选乙,因为乙有4次在99分以上.解:(1)甲的中位数==94.5,乙的众数是99;(2)从稳定性看:甲考试成绩较稳定,因为方差,极差较小;从平均数看:甲的平均数比乙的平均数高;乙有潜力,因为乙的最好成绩比甲的最好成绩高.从众数看:乙的成绩比甲好.从中位数看:甲比乙的成绩好.(3)10次测验,甲有8次不少于90分,而乙仅有6次,若想获奖可能性较大,可选甲参赛;
若想拿到更好的名次可选乙,因为乙有4次在99分以上.
参考答案:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
