7.2.2用坐标表示平移课件
图片预览



文档简介
(共23张PPT)
2.连接各组对应点的线段平行且相等。
1.平移变换不改变图形的形状、大小;
回
顾
与
复
习
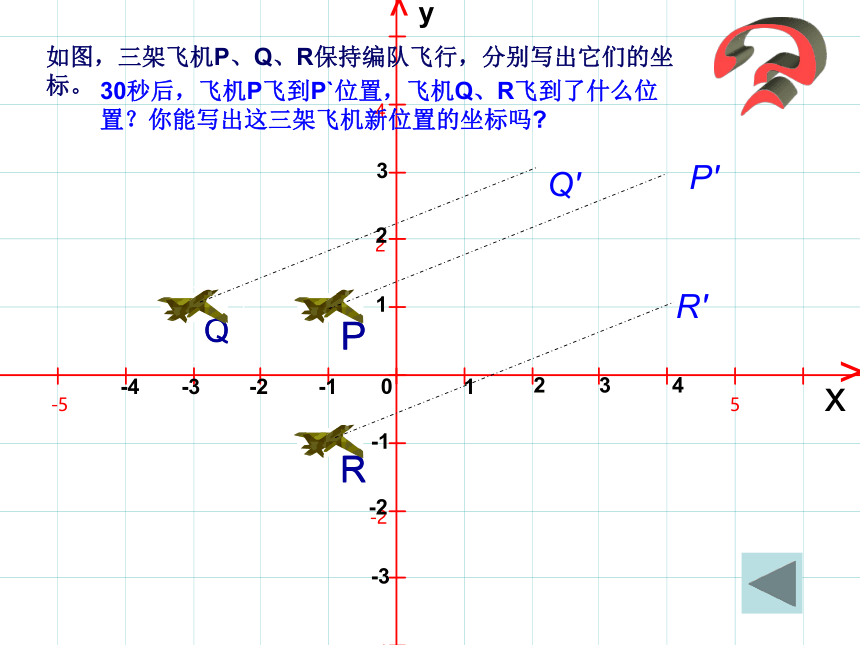
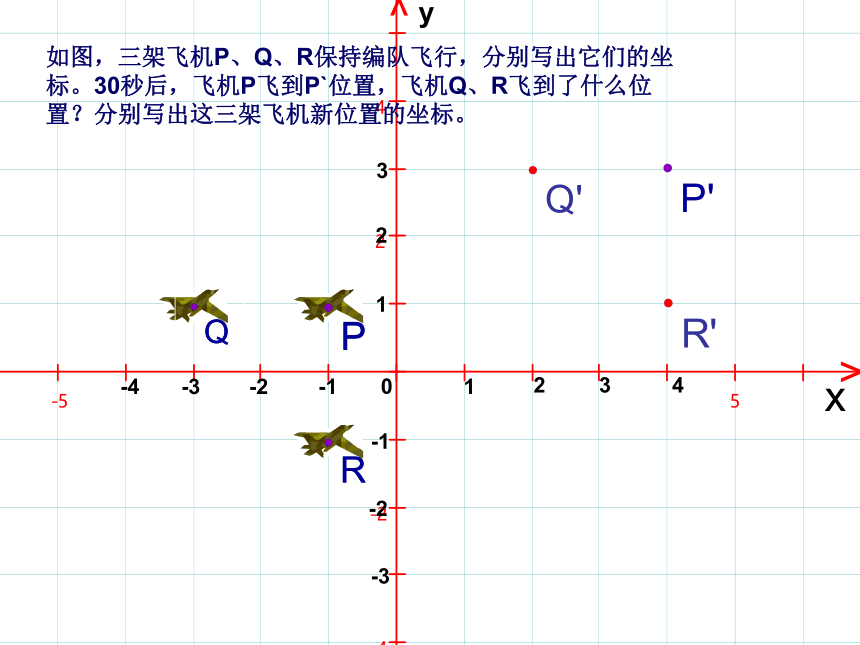
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗
Q′
P′
R′
-3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
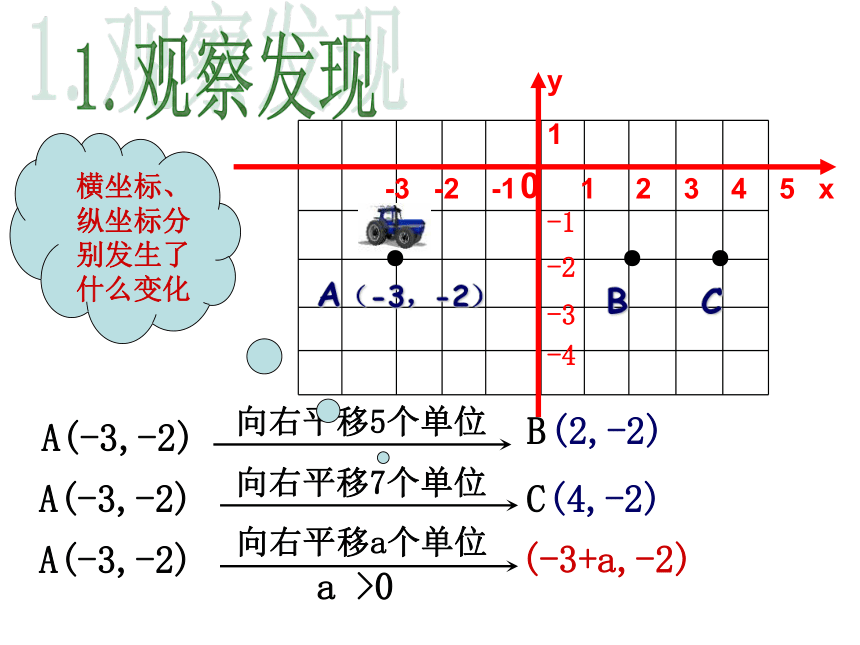
A(-3,-2)
A(-3,-2)
向右平移5个单位
B
(2,-2)
B
C
A(-3,-2)
向右平移7个单位
C
(4,-2)
(-3+a,-2)
A(-3,-2)
向右平移a个单位
a >0
横坐标、纵坐标分别发生了什么变化
●
●
●
-4- 3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
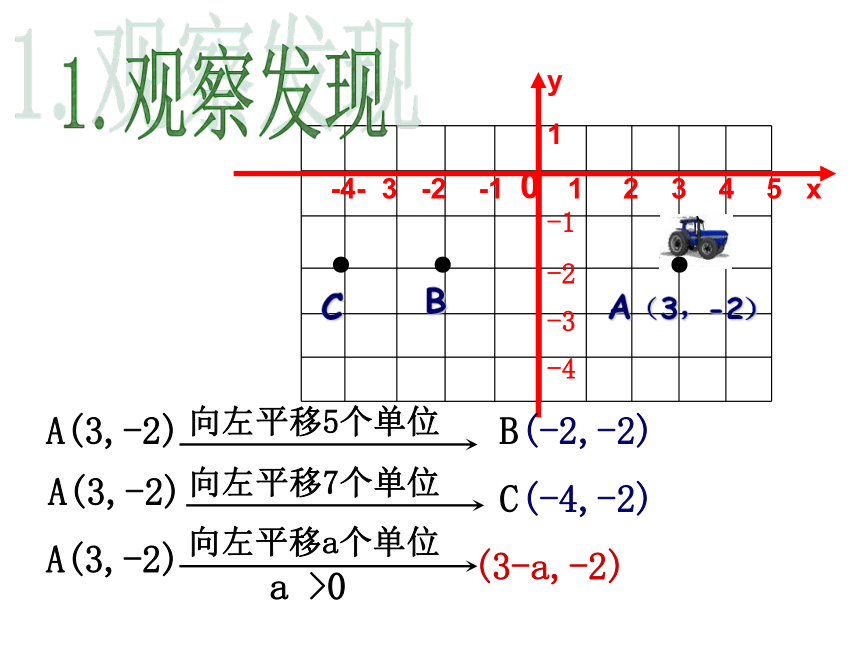
A(3,-2)
A(3,-2)
向左平移5个单位
B
(-2,-2)
B
C
A(3,-2)
向左平移7个单位
C
(-4,-2)
(3-a,-2)
A(3,-2)
向左平移a个单位
a >0
●
●
●
B′
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
A
B
A′
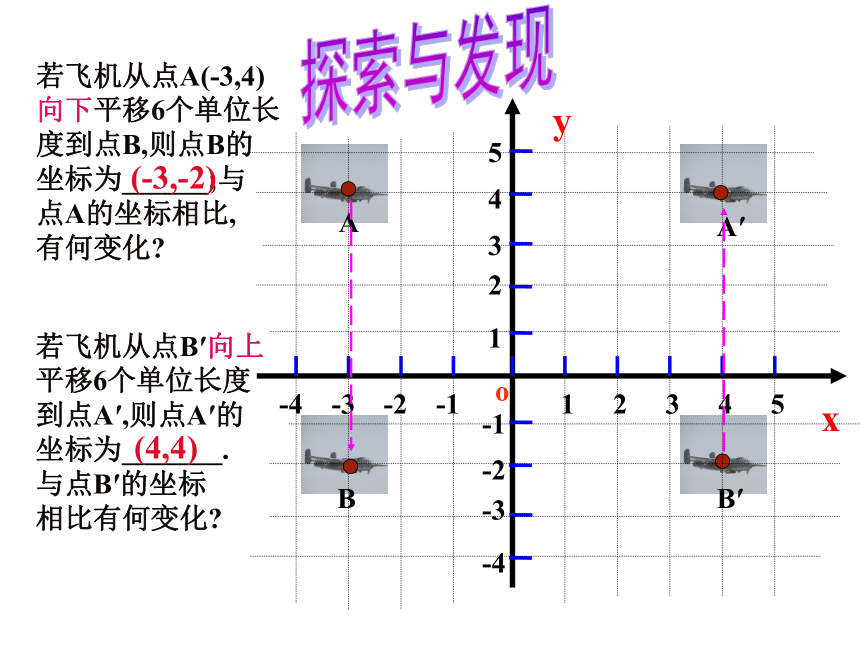
若飞机从点A(-3,4)
向下平移6个单位长
度到点B,则点B的
坐标为______;与
点A的坐标相比,
有何变化
若飞机从点B′向上
平移6个单位长度
到点A′,则点A′的
坐标为_______.
与点B′的坐标
相比有何变化
(-3,-2)
(4,4)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
总结规律1:图形平移与点的坐标变化 间的关系
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?分别写出这三架飞机新位置的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
探索图形上点的坐标变化与图形平移间的关系
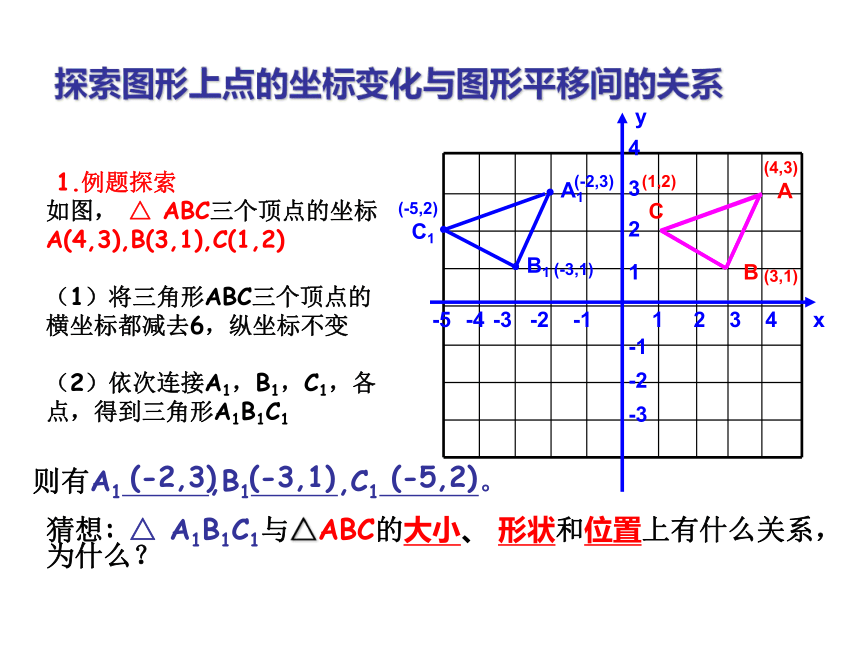
1.例题探索
如图, △ ABC三个顶点的坐标
A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
(2)依次连接A1,B1,C1,各
点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
^
y
>
x
0
1
1
4
3
2
2
3
4
5
-6
-5
-4
-3
-2
-1
-1
-2
-3
-4
如果将三角形ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,这时图形在哪儿?把它画出来!
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2
在平面直角坐标系中,有一点P(-9,6),
若将P:
(1)向左平移2个单位长度,所得点的坐标为______;
(2)向右平移3个单位长度,所得点的坐标为______;
(3)向下平移4个单位长度,所得点的坐标为______;
(4)向上平移3个单位长度,所得点的坐标为______;
1.将点A(-3,2)向下平移3个单位,
再向右平移4个单位得点B,则B点坐
标是
2.将点P(0,-2)向左平移2个单位,
再向上平移4个单位得点Q(x,y),则
xy=
(1,-1)
-4
1、如果A,B的坐标分别为A(-4,5),B(-4,2),将点A向___平移___个单位长度得到点B;将点B向___平移___个单位长度得到点A 。
2、如果P、Q的坐标分别为P(-3,-5),Q(2,-5),,将点P向___平移___个单位长度得到点Q;将点Q向___平移___个单位长度得到点P。
下
3
上
3
右
5
左
5
线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
(1,2)
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
有相距5个单位的两点 A(-3,a),B(b,4),
AB//x轴,则a= ___ ,b= ___ 。
A
B
4
2或-8
1.将点P(m,1)向右平移5个单位长度,得
到点Q(3,1),则点P坐标为
(-2,1)
2.将点P(m+1,n -2)向上平移3个单位长
度,得到点Q(2,1- n),则点A(m,n)坐
标为
解:m +1=2 ,
n -2 +3 =1- n
故,m=1,n=0
所以,点A坐标为(1,0)
(1,0)
如图△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移到△A1B1C1。
求A1、B1、C1的坐标
(2)
A1(3,6)
B1(1,4)
C1(7,3)
(1)
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(3)
0
(2)
小
结
如图与(1)比较,请抢答:
(2)(3)中的三角形发生了哪些变化?
图中直角三角形的顶点坐标分别了什么变化?
回顾所学
你能运用图形尽可能具体地对今天所学的知识进行一番回顾吗
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
A(-2,4)
知识要点
图形平移与点的坐标变化间的关系,以及图形上点的坐标变化与图形平移间的关系
作业:习题7.2 第5、6、7题
谢谢观赏, 欢迎指导!
2.连接各组对应点的线段平行且相等。
1.平移变换不改变图形的形状、大小;
回
顾
与
复
习
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?你能写出这三架飞机新位置的坐标吗
Q′
P′
R′
-3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(-3,-2)
A(-3,-2)
向右平移5个单位
B
(2,-2)
B
C
A(-3,-2)
向右平移7个单位
C
(4,-2)
(-3+a,-2)
A(-3,-2)
向右平移a个单位
a >0
横坐标、纵坐标分别发生了什么变化
●
●
●
-4- 3 -2 -1 1 2 3 4 5 x
y
0
1
-1
-2
-3
-4
A(3,-2)
A(3,-2)
向左平移5个单位
B
(-2,-2)
B
C
A(3,-2)
向左平移7个单位
C
(-4,-2)
(3-a,-2)
A(3,-2)
向左平移a个单位
a >0
●
●
●
B′
3
1
4
2
5
-2
-4
-1
-3
o
1
2
3
4
5
-4
-3
-2
-1
x
y
A
B
A′
若飞机从点A(-3,4)
向下平移6个单位长
度到点B,则点B的
坐标为______;与
点A的坐标相比,
有何变化
若飞机从点B′向上
平移6个单位长度
到点A′,则点A′的
坐标为_______.
与点B′的坐标
相比有何变化
(-3,-2)
(4,4)
(1)左、右平移:
向右平移a个单位
(2)上、下平移:
原图形上的点(x,y) ,
向左平移a个单位
原图形上的点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
向下平移b个单位
原图形上的点(x,y) ,
(x,y+b)
(x,y-b)
总结规律1:图形平移与点的坐标变化 间的关系
如图,三架飞机P、Q、R保持编队飞行,分别写出它们的坐标。30秒后,飞机P飞到P`位置,飞机Q、R飞到了什么位置?分别写出这三架飞机新位置的坐标。
^
y
>
x
0
1
1
2
3
4
3
2
-1
-2
-3
-1
-2
-3
-4
探索图形上点的坐标变化与图形平移间的关系
1.例题探索
如图, △ ABC三个顶点的坐标
A(4,3),B(3,1),C(1,2)
(1)将三角形ABC三个顶点的
横坐标都减去6,纵坐标不变
(2)依次连接A1,B1,C1,各
点,得到三角形A1B1C1
猜想: △ A1B1C1与△ABC的大小、 形状和位置上有什么关系,为什么?
则有A1 ,B1 ,C1 。
(-2,3)
(-3,1)
(-5,2)
-3 -2 -1 1 2 3 4 x
3
2
1
-2
-1
-3
4
y
A
B
C
-5
-4
A1
B1
C1
(4,3)
(1,2)
(3,1)
(-2,3)
(-3,1)
(-5,2)
^
y
>
x
0
1
1
4
3
2
2
3
4
5
-6
-5
-4
-3
-2
-1
-1
-2
-3
-4
如果将三角形ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,这时图形在哪儿?把它画出来!
(1)横坐标变化,纵坐标不变:
向右平移a个单位
原图形上的点(x,y) ,
(x+a,y)
图形上点的坐标变化与图形平移间的关系
向左平移a个单位
原图形上的点(x,y) ,
(x-a,y)
向上平移b个单位
原图形上的点(x,y) ,
(x,y+b)
向下平移b个单位
原图形上的点(x,y) ,
(x,y-b)
(2)横坐标不变,纵坐标变化:
总结规律2
在平面直角坐标系中,有一点P(-9,6),
若将P:
(1)向左平移2个单位长度,所得点的坐标为______;
(2)向右平移3个单位长度,所得点的坐标为______;
(3)向下平移4个单位长度,所得点的坐标为______;
(4)向上平移3个单位长度,所得点的坐标为______;
1.将点A(-3,2)向下平移3个单位,
再向右平移4个单位得点B,则B点坐
标是
2.将点P(0,-2)向左平移2个单位,
再向上平移4个单位得点Q(x,y),则
xy=
(1,-1)
-4
1、如果A,B的坐标分别为A(-4,5),B(-4,2),将点A向___平移___个单位长度得到点B;将点B向___平移___个单位长度得到点A 。
2、如果P、Q的坐标分别为P(-3,-5),Q(2,-5),,将点P向___平移___个单位长度得到点Q;将点Q向___平移___个单位长度得到点P。
下
3
上
3
右
5
左
5
线段CD是由线段AB平移得到的。
点A(–1,4)的对应点为C(4,7),则点B(–4,–1)的对应点D的坐标为________。
(1,2)
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
有相距5个单位的两点 A(-3,a),B(b,4),
AB//x轴,则a= ___ ,b= ___ 。
A
B
4
2或-8
1.将点P(m,1)向右平移5个单位长度,得
到点Q(3,1),则点P坐标为
(-2,1)
2.将点P(m+1,n -2)向上平移3个单位长
度,得到点Q(2,1- n),则点A(m,n)坐
标为
解:m +1=2 ,
n -2 +3 =1- n
故,m=1,n=0
所以,点A坐标为(1,0)
(1,0)
如图△ABC中任意一点P(x0,y0)经平移后对应点为P1(x0+5,y0+3),将△ABC作同样的平移到△A1B1C1。
求A1、B1、C1的坐标
(2)
A1(3,6)
B1(1,4)
C1(7,3)
(1)
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
0
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
2
1
-1
-2
-3
-4
-2
2
4
1
2
3
4
-
1
-
2
-
3
-
4
1
2
-
1
-
2
-
3
x
y
(3)
0
(2)
小
结
如图与(1)比较,请抢答:
(2)(3)中的三角形发生了哪些变化?
图中直角三角形的顶点坐标分别了什么变化?
回顾所学
你能运用图形尽可能具体地对今天所学的知识进行一番回顾吗
x
Y
0
1
4
2
3
-4
-1
-3
-2
1
4
2
3
-1
-2
-3
A(-2,4)
知识要点
图形平移与点的坐标变化间的关系,以及图形上点的坐标变化与图形平移间的关系
作业:习题7.2 第5、6、7题
谢谢观赏, 欢迎指导!
