19.2.2 课时1一次函数 同步练习
图片预览


文档简介
《一次函数》练习
一、选择——基础知识运用
1.在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是( )21世纪教育网版权所有
A.正比例函数 B.反比例函数
C.图象不经过原点的一次函数 D.二次函数
2.下列函数中,y是x的一次函数的是( )
①y=x-6;②y= ;③y= ;④y=7-x.
A.①②③ B.①③④ C.①②③④ D.②③④
3.如果y=(m-2)xm2?3+2是一次函数,那么m的值是( )
A.2 B.-2 C.±2 D.±
4.一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A. B.
C. D.
5.下列函数图象不可能是一次函数y=ax-(a-2)图象的是( )
A. B.
C. D.
二、解答——知识提高运用
6.如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0)。21教育网
(1)直线AB的解析式为 。
(2)点A的坐标为 ,AC的长为 。
(3)若动点P(x,y)在直线AB上,则△PAC中AC边上的高= (用含x的式子表示),其中x的取值范围为 。21cnjy.com
(4)若△PAC的面积为6,试确定点P的坐标。
7.作出函数y=|3x-5|的图象。
8.已知一次函数y=(4-k)x-2k2+32。
(1)k为何值时,它的图象经过原点;
(2)k为何值时,它的图象经过点(0,-2);
(3)k为何值时,它的图象平行于直线y=-x;
(4)k为何值时,y随x的增大而减小。
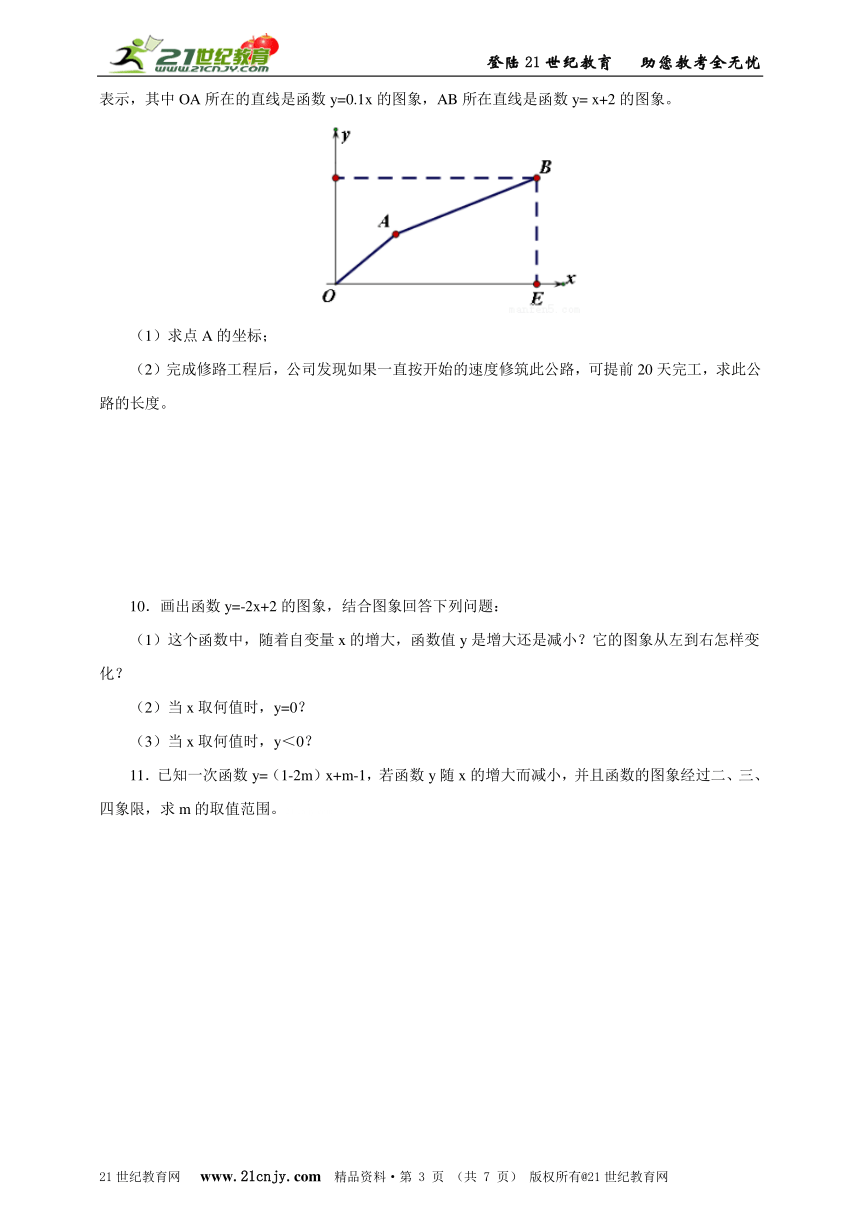
9.翔志琼公司修筑一条公路,开始修筑若干天以后,公司抽调了一部力量去完成其他任务,所以施工速度有所降低。修筑公路的里程y(千米)和所用时间x(天)的关系用下图所示的折线OAB表示,其中OA所在的直线是函数y=0.1x的图象,AB所在直线是函数y= x+2的图象。
(1)求点A的坐标;
(2)完成修路工程后,公司发现如果一直按开始的速度修筑此公路,可提前20天完工,求此公路的长度。
10.画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)这个函数中,随着自变量x的增大,函数值y是增大还是减小?它的图象从左到右怎样变化?
(2)当x取何值时,y=0?
(3)当x取何值时,y<0?
11.已知一次函数y=(1-2m)x+m-1,若函数y随x的增大而减小,并且函数的图象经过二、三、四象限,求m的取值范围。21·cn·jy·com
参考答案
一、选择——基础知识运用
1.【答案】A
【解析】设原来溶液中糖和水分别有ag和bg。
根据题意可知x:y=a:b,整理得:y=x。
故选:A。
2.【答案】B
【解析】①y=x-6符合一次函数的定义,故本选项正确;
②y=是反比例函数;故本选项错误;
③y= ,属于正比例函数,是一次函数的特殊形式,故本选项正确;
④y=7-x符合一次函数的定义,故本选项正确;
综上所述,符合题意的是①③④;
故选B。
3.【答案】B
【解析】∵y=(m-2)xm2?3+2是一次函数,
∴m2-3=1,m-2≠0,
解得m=-2。
故选:B。
4.【答案】C
【解析】(1)当m>0,n>0时,mn>0,
一次函数y=mx+n的图象一、二、三象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(2)当m>0,n<0时,mn<0,
一次函数y=mx+n的图象一、三、四象限,
正比例函数y=mnx的图象过二、四象限,C选项符合;
(3)当m<0,n<0时,mn>0,
一次函数y=mx+n的图象二、三、四象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(4)当m<0,n>0时,mn<0,
一次函数y=mx+n的图象一、二、四象限,
正比例函数y=mnx的图象过二、四象限,无符合项。
故选C。
5.【答案】B
【解析】根据图象知:
A、a>0,-(a-2)>0.解得0<a<2,所以有可能;
B、a<0,-(a-2)<0.解得两不等式没有公共部分,所以不可能;
C、a<0,-(a-2)>0.解得a<0,所以有可能;
D、a>0,-(a-2)<0.解得a>2,所以有可能。
故选B。
二、解答——知识提高运用
6.【答案】(1)∵点B在直线y=-2x+b的图象上,
∴4=-2×0+b,b=4,
∴直线AB的解析式为y=-2x+4。
故答案为:y=-2x+4。
(2)令y=-2x+4中的y=0,
则有0=-2x+4,解得:x=2。
∴点A的坐标为(2,0),AC=2-(-4)=6.
故答案为:(2,0);6。
(3)∵AC边在x轴上,且点P的坐标为(x,y),
∴△PAC中AC边上的高=|y|=|-2x+4|。
∵y≠0,即-2x+4≠0,
解得:x≠2。
故答案为:|-2x+4|;x≠2。
(4)∵AC=6,
∴S△PAC= AC?|y|=6,
解得:y=±2,
当y=2时,有-2x+4=2,解得:x=1;
当y=-2时,有-2x+4=-2,解得:x=3.
故点P的坐标为(1,2)或(3,-2)。
7.【答案】当3x-5<0时,y=-3x+5,
当3x-5≥0时,y=3x-5,
分别在同一坐标系内作这两个函数在相应自变量范围内的图象,
如图所示:
8.【答案】(1)∵一次函数y=(4-k)x-2k2+32的图象经过原点,
∴-2k2+32=0
解得:k=±4
∵4-k≠0
∴k=-4;
(2)∵一次函数y=(4-k)x-2k2+32的图象经过(0,-2),
∴-2k2+32=-2
解得:k=±
(3)∵一次函数y=(4-k)x-2k2+32的图象平行于直线y=-x,
∴4-k=-1
∴k=5;
(4)∵一次函数y=(4-k)x-2k2+32中y随x的增大而减小
∴4-k<0
∴k>4。
9.【答案】(1)由题意得
y=0.1x;,y= x+2
解得:x=60;y=6
点A的坐标为(60,6);
(2)由y=0.1x,y=x+2得
x=10y,x=15(y﹣2),
根据题意得:
15(y﹣2)﹣10y=20
解得y=10
答:此公路的长度为10千米。
10.【答案】函数y=-2x+2的图象为:
(1)由图象知:这个函数中,随着x的增大,y将减小,图象从左向右下降。
(2)由图象知:当x=1时,y=0。
(3)由图象知:当x>1时,y<0。
11.【答案】根据一次函数的性质,函数y随x的增大而减小,则1-2m<0,
解得m>;
函数的图象经过二、三、四象限,说明图象与y轴的交点在x轴下方,即m-1<0,
解得m<1;
所以m的取值范围为:<m<1。
一、选择——基础知识运用
1.在糖水中继续放入糖x(g)、水y(g),并使糖完全溶解,如果甜度保持不变,那么y与x的函数关系一定是( )21世纪教育网版权所有
A.正比例函数 B.反比例函数
C.图象不经过原点的一次函数 D.二次函数
2.下列函数中,y是x的一次函数的是( )
①y=x-6;②y= ;③y= ;④y=7-x.
A.①②③ B.①③④ C.①②③④ D.②③④
3.如果y=(m-2)xm2?3+2是一次函数,那么m的值是( )
A.2 B.-2 C.±2 D.±
4.一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )
A. B.
C. D.
5.下列函数图象不可能是一次函数y=ax-(a-2)图象的是( )
A. B.
C. D.
二、解答——知识提高运用
6.如图,直线y=-2x+b与x轴,y轴分别相交于A、B两点,点B的坐标为(0,4),点C的坐标为(-4,0)。21教育网
(1)直线AB的解析式为 。
(2)点A的坐标为 ,AC的长为 。
(3)若动点P(x,y)在直线AB上,则△PAC中AC边上的高= (用含x的式子表示),其中x的取值范围为 。21cnjy.com
(4)若△PAC的面积为6,试确定点P的坐标。
7.作出函数y=|3x-5|的图象。
8.已知一次函数y=(4-k)x-2k2+32。
(1)k为何值时,它的图象经过原点;
(2)k为何值时,它的图象经过点(0,-2);
(3)k为何值时,它的图象平行于直线y=-x;
(4)k为何值时,y随x的增大而减小。
9.翔志琼公司修筑一条公路,开始修筑若干天以后,公司抽调了一部力量去完成其他任务,所以施工速度有所降低。修筑公路的里程y(千米)和所用时间x(天)的关系用下图所示的折线OAB表示,其中OA所在的直线是函数y=0.1x的图象,AB所在直线是函数y= x+2的图象。
(1)求点A的坐标;
(2)完成修路工程后,公司发现如果一直按开始的速度修筑此公路,可提前20天完工,求此公路的长度。
10.画出函数y=-2x+2的图象,结合图象回答下列问题:
(1)这个函数中,随着自变量x的增大,函数值y是增大还是减小?它的图象从左到右怎样变化?
(2)当x取何值时,y=0?
(3)当x取何值时,y<0?
11.已知一次函数y=(1-2m)x+m-1,若函数y随x的增大而减小,并且函数的图象经过二、三、四象限,求m的取值范围。21·cn·jy·com
参考答案
一、选择——基础知识运用
1.【答案】A
【解析】设原来溶液中糖和水分别有ag和bg。
根据题意可知x:y=a:b,整理得:y=x。
故选:A。
2.【答案】B
【解析】①y=x-6符合一次函数的定义,故本选项正确;
②y=是反比例函数;故本选项错误;
③y= ,属于正比例函数,是一次函数的特殊形式,故本选项正确;
④y=7-x符合一次函数的定义,故本选项正确;
综上所述,符合题意的是①③④;
故选B。
3.【答案】B
【解析】∵y=(m-2)xm2?3+2是一次函数,
∴m2-3=1,m-2≠0,
解得m=-2。
故选:B。
4.【答案】C
【解析】(1)当m>0,n>0时,mn>0,
一次函数y=mx+n的图象一、二、三象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(2)当m>0,n<0时,mn<0,
一次函数y=mx+n的图象一、三、四象限,
正比例函数y=mnx的图象过二、四象限,C选项符合;
(3)当m<0,n<0时,mn>0,
一次函数y=mx+n的图象二、三、四象限,
正比例函数y=mnx的图象过一、三象限,无符合项;
(4)当m<0,n>0时,mn<0,
一次函数y=mx+n的图象一、二、四象限,
正比例函数y=mnx的图象过二、四象限,无符合项。
故选C。
5.【答案】B
【解析】根据图象知:
A、a>0,-(a-2)>0.解得0<a<2,所以有可能;
B、a<0,-(a-2)<0.解得两不等式没有公共部分,所以不可能;
C、a<0,-(a-2)>0.解得a<0,所以有可能;
D、a>0,-(a-2)<0.解得a>2,所以有可能。
故选B。
二、解答——知识提高运用
6.【答案】(1)∵点B在直线y=-2x+b的图象上,
∴4=-2×0+b,b=4,
∴直线AB的解析式为y=-2x+4。
故答案为:y=-2x+4。
(2)令y=-2x+4中的y=0,
则有0=-2x+4,解得:x=2。
∴点A的坐标为(2,0),AC=2-(-4)=6.
故答案为:(2,0);6。
(3)∵AC边在x轴上,且点P的坐标为(x,y),
∴△PAC中AC边上的高=|y|=|-2x+4|。
∵y≠0,即-2x+4≠0,
解得:x≠2。
故答案为:|-2x+4|;x≠2。
(4)∵AC=6,
∴S△PAC= AC?|y|=6,
解得:y=±2,
当y=2时,有-2x+4=2,解得:x=1;
当y=-2时,有-2x+4=-2,解得:x=3.
故点P的坐标为(1,2)或(3,-2)。
7.【答案】当3x-5<0时,y=-3x+5,
当3x-5≥0时,y=3x-5,
分别在同一坐标系内作这两个函数在相应自变量范围内的图象,
如图所示:
8.【答案】(1)∵一次函数y=(4-k)x-2k2+32的图象经过原点,
∴-2k2+32=0
解得:k=±4
∵4-k≠0
∴k=-4;
(2)∵一次函数y=(4-k)x-2k2+32的图象经过(0,-2),
∴-2k2+32=-2
解得:k=±
(3)∵一次函数y=(4-k)x-2k2+32的图象平行于直线y=-x,
∴4-k=-1
∴k=5;
(4)∵一次函数y=(4-k)x-2k2+32中y随x的增大而减小
∴4-k<0
∴k>4。
9.【答案】(1)由题意得
y=0.1x;,y= x+2
解得:x=60;y=6
点A的坐标为(60,6);
(2)由y=0.1x,y=x+2得
x=10y,x=15(y﹣2),
根据题意得:
15(y﹣2)﹣10y=20
解得y=10
答:此公路的长度为10千米。
10.【答案】函数y=-2x+2的图象为:
(1)由图象知:这个函数中,随着x的增大,y将减小,图象从左向右下降。
(2)由图象知:当x=1时,y=0。
(3)由图象知:当x>1时,y<0。
11.【答案】根据一次函数的性质,函数y随x的增大而减小,则1-2m<0,
解得m>;
函数的图象经过二、三、四象限,说明图象与y轴的交点在x轴下方,即m-1<0,
解得m<1;
所以m的取值范围为:<m<1。
