陕西省黄陵中学2016-2017学年高二4月月考数学(理)试题(普通班) Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2016-2017学年高二4月月考数学(理)试题(普通班) Word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 221.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-29 00:00:00 | ||
图片预览


文档简介
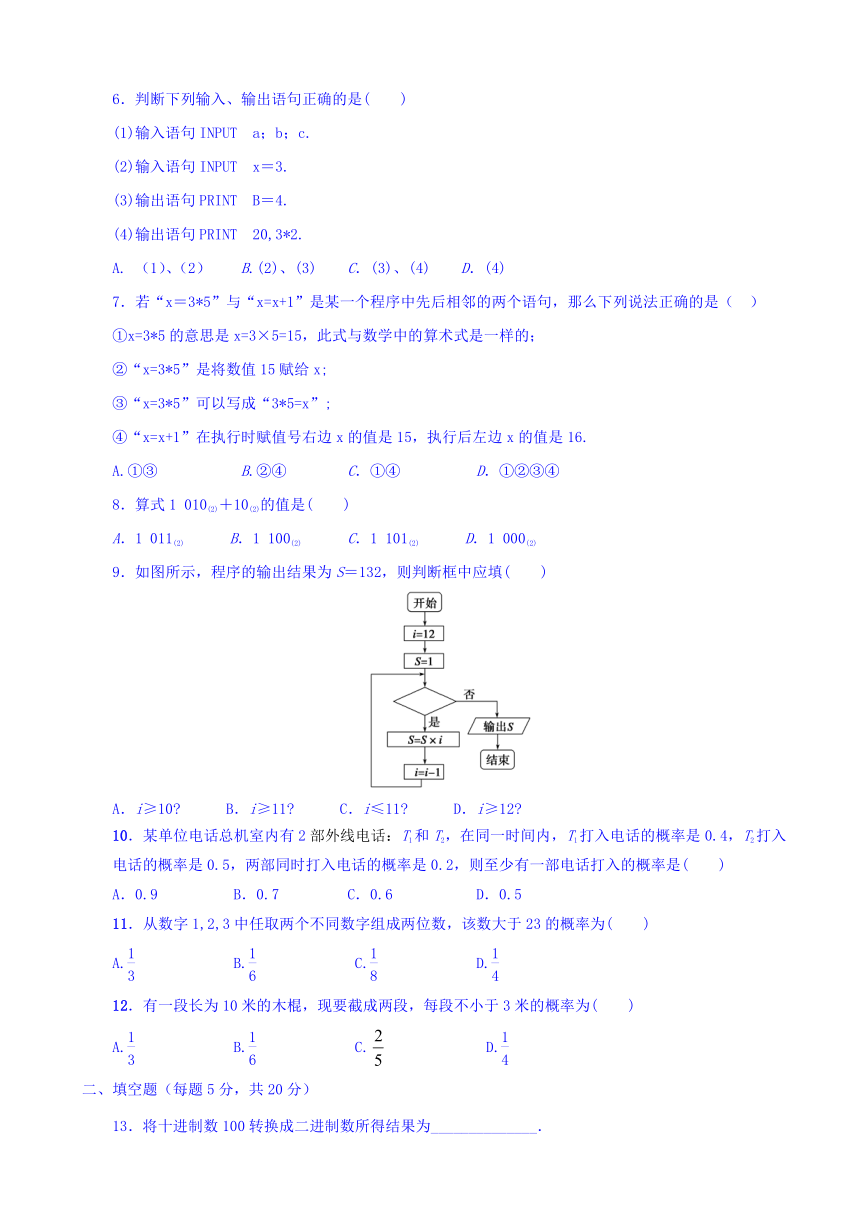
高二普通班数学(理科)第二学月月考试题
一、选择题(每题5分,共60分)
1.下列关于算法的说法正确的有( )
①求解某一类问题的算法是唯一的;
②算法必须在有限步操作之后停止;
③算法的每一步操作必须是明确的,不能有歧义;
④算法执行后一定产生明确的结果.
A.1个
B.2个
C.3个
D.4个
2.下边是一个算法的程序框图,当输入的x值为3时,输出y的结果恰好是,则处的关系式是( )
A.y=x3
B.y=3-x
C.y=3x
D.y=x
3.使用秦九韶算法求P(x)=anxn+an-1xn-1+…+a1x+a0在x=x0时的值可减少运算次数,做加法和乘法的次数分别是( )
A.n,n
B.n,
C.n,2n+1
D.2n+1,
4.对满足A
B的非空集合A、B有下列四个命题:
①若任取x∈A,则x∈B是必然事件;
②若x A,则x∈B是不可能事件;
③若任取x∈B,则x∈A是随机事件;
④若x B,则x A是必然事件,其正确命题的个数为( )
A.4
B.3
C.2
D.1
5.下列说法正确的是( )
A.任何事件的概率总是在(0,1)之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
6.判断下列输入、输出语句正确的是( )
(1)输入语句INPUT a;b;c.
(2)输入语句INPUT x=3.
(3)输出语句PRINT B=4.
(4)输出语句PRINT 20,3
2.
A.
(1)、(2)
B.(2)、(3)
C.(3)、(4)
D.(4)
7.若“x=3
5”与“x=x+1”是某一个程序中先后相邻的两个语句,那么下列说法正确的是(
)
①x=3
5的意思是x=3×5=15,此式与数学中的算术式是一样的;
②“x=3
5”是将数值15赋给x;
③“x=3
5”可以写成“3
5=x”;
④“x=x+1”在执行时赋值号右边x的值是15,执行后左边x的值是16.
A.①③
B.②④
C.①④
D.①②③④
8.算式1
010(2)+10(2)的值是( )
A.1
011(2)
B.1
100(2)
C.1
101(2)
D.1
000(2)
9.如图所示,程序的输出结果为S=132,则判断框中应填( )
A.i≥10
B.i≥11
C.i≤11
D.i≥12
10.某单位电话总机室内有2部外线电话:T1和T2,在同一时间内,T1打入电话的概率是0.4,T2打入电话的概率是0.5,两部同时打入电话的概率是0.2,则至少有一部电话打入的概率是( )
A.0.9
B.0.7
C.0.6
D.0.5
11.从数字1,2,3中任取两个不同数字组成两位数,该数大于23的概率为( )
A.
B.
C.
D.
12.有一段长为10米的木棍,现要截成两段,每段不小于3米的概率为(
)
A.
B.
C.
D.
二、填空题(每题5分,共20分)
13.将十进制数100转换成二进制数所得结果为______________.
14.下边程序运行后,输出的值为________.
15.三个数72、120、168的最大公约数是________.
16.有1杯2
L的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1
L,这一小杯水中含有细菌的概率是________.
三、解答题(17.18.19.20.21每题12分,22每题10分,共70分)
17.某校举行运动会,高二·一班有男乒乓球运动员4名,女乒乓球运动员3名,现要选一男一女运动员组成混合双打组合代表本班参赛,试列出全部可能的结果,若某女乒乓球运动员为国家一级运动员,则她参赛的概率是多少?
18.黄种人群中各种血型的人所占的比例如下:
血型
A
B
AB
O
该血型的人所占比例(%)
28
29
8
35
已知同种血型的人可以输血,O型血可以输给任一种血型的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
19.已知函数y=,试编写程序,输入x的值后输出y的值.
20.下列语句是求S=2+3+4+…+99的一个程序.请回答问题:
(1)程序中是否有错误?若有请加以改正;
(2)把程序改成另一种类型的循环语句.
21.在闭区间上任取两个实数,则它们的和不大于1的概率是多少?
22.(10分)画出求12-22+32-42+…+992-1002的值的程序框图.
答案
一、选择题(每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
A
B
C
D
B
B
B
B
A
C
二、填空题(每题5分,共20分)
;
14.
120
;
24
;
16.
;
三、
17.解 由于男生从4人中任意选取,女生从3人中任意选取,为了得到试验的全部结果,我们设男生为A,B,C,D,女生为1,2,3,我们可以用一个“数对”来表示随机选取的结果.如(A,1)表示:从男生中随机选取的是男生A,从女生中选取的是女生1,可用列举法列出所有可能的结果.如下表所示,设“国家一级运动员参赛”为事件E.
1
2
3
A
(A,1)
(A,2)
(A,3)
B
(B,1)
(B,2)
(B,3)
C
(C,1)
(C,2)
(C,3)
D
(D,1)
(D,2)
(D,3)
由上表可知,可能的结果总数是12个.设该国家一级运动员为编号1,她参赛的可能事件有4个,故她参赛的概率为P(E)==.
18.解 (1)对任一人,其血型为A、B、AB、O型血的事件分别记为A′、B′、C′、D′,它们是互斥的.由已知,有
P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.
因为B、O型血可以输给B型血的人,故“可以输给B型血的人”为事件B′∪D′.根据互斥事件的加法公式,有
P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64.
(2)由于A、AB型血不能输给B型血的人,故“不能输给B型血的人”为事件A′∪C′,且P(A′∪C′)=P(A′)+P(C′)=0.28+0.08=0.36.
答 任找一人,其血可以输给小明的概率为0.64,其血不能输给小明的概率为0.36.
19.解 程序为:
INPUT
x IF
x>0
THEN y=2
x^2-1
ELSE
IF
x=0
THEN
y=2
x+1
ELSE
y=-2
x^2+4
END
IF
END
IF
PRINT
y
END
20.解 (1)有两处错误:
①语句i=1应为i=2.
②语句LOOP
UNTIL
i>=99应为LOOP
UNTIL
i>99
(2)改为WHILE型循环语句
21.答案.
解析
如图所示
P==.
22.答案。
女
结
果
男
一、选择题(每题5分,共60分)
1.下列关于算法的说法正确的有( )
①求解某一类问题的算法是唯一的;
②算法必须在有限步操作之后停止;
③算法的每一步操作必须是明确的,不能有歧义;
④算法执行后一定产生明确的结果.
A.1个
B.2个
C.3个
D.4个
2.下边是一个算法的程序框图,当输入的x值为3时,输出y的结果恰好是,则处的关系式是( )
A.y=x3
B.y=3-x
C.y=3x
D.y=x
3.使用秦九韶算法求P(x)=anxn+an-1xn-1+…+a1x+a0在x=x0时的值可减少运算次数,做加法和乘法的次数分别是( )
A.n,n
B.n,
C.n,2n+1
D.2n+1,
4.对满足A
B的非空集合A、B有下列四个命题:
①若任取x∈A,则x∈B是必然事件;
②若x A,则x∈B是不可能事件;
③若任取x∈B,则x∈A是随机事件;
④若x B,则x A是必然事件,其正确命题的个数为( )
A.4
B.3
C.2
D.1
5.下列说法正确的是( )
A.任何事件的概率总是在(0,1)之间
B.频率是客观存在的,与试验次数无关
C.随着试验次数的增加,频率一般会越来越接近概率
D.概率是随机的,在试验前不能确定
6.判断下列输入、输出语句正确的是( )
(1)输入语句INPUT a;b;c.
(2)输入语句INPUT x=3.
(3)输出语句PRINT B=4.
(4)输出语句PRINT 20,3
2.
A.
(1)、(2)
B.(2)、(3)
C.(3)、(4)
D.(4)
7.若“x=3
5”与“x=x+1”是某一个程序中先后相邻的两个语句,那么下列说法正确的是(
)
①x=3
5的意思是x=3×5=15,此式与数学中的算术式是一样的;
②“x=3
5”是将数值15赋给x;
③“x=3
5”可以写成“3
5=x”;
④“x=x+1”在执行时赋值号右边x的值是15,执行后左边x的值是16.
A.①③
B.②④
C.①④
D.①②③④
8.算式1
010(2)+10(2)的值是( )
A.1
011(2)
B.1
100(2)
C.1
101(2)
D.1
000(2)
9.如图所示,程序的输出结果为S=132,则判断框中应填( )
A.i≥10
B.i≥11
C.i≤11
D.i≥12
10.某单位电话总机室内有2部外线电话:T1和T2,在同一时间内,T1打入电话的概率是0.4,T2打入电话的概率是0.5,两部同时打入电话的概率是0.2,则至少有一部电话打入的概率是( )
A.0.9
B.0.7
C.0.6
D.0.5
11.从数字1,2,3中任取两个不同数字组成两位数,该数大于23的概率为( )
A.
B.
C.
D.
12.有一段长为10米的木棍,现要截成两段,每段不小于3米的概率为(
)
A.
B.
C.
D.
二、填空题(每题5分,共20分)
13.将十进制数100转换成二进制数所得结果为______________.
14.下边程序运行后,输出的值为________.
15.三个数72、120、168的最大公约数是________.
16.有1杯2
L的水,其中含有1个细菌,用一个小杯从这杯水中取出0.1
L,这一小杯水中含有细菌的概率是________.
三、解答题(17.18.19.20.21每题12分,22每题10分,共70分)
17.某校举行运动会,高二·一班有男乒乓球运动员4名,女乒乓球运动员3名,现要选一男一女运动员组成混合双打组合代表本班参赛,试列出全部可能的结果,若某女乒乓球运动员为国家一级运动员,则她参赛的概率是多少?
18.黄种人群中各种血型的人所占的比例如下:
血型
A
B
AB
O
该血型的人所占比例(%)
28
29
8
35
已知同种血型的人可以输血,O型血可以输给任一种血型的人,其他不同血型的人不能互相输血,小明是B型血,若小明因病需要输血,问:
(1)任找一个人,其血可以输给小明的概率是多少?
(2)任找一个人,其血不能输给小明的概率是多少?
19.已知函数y=,试编写程序,输入x的值后输出y的值.
20.下列语句是求S=2+3+4+…+99的一个程序.请回答问题:
(1)程序中是否有错误?若有请加以改正;
(2)把程序改成另一种类型的循环语句.
21.在闭区间上任取两个实数,则它们的和不大于1的概率是多少?
22.(10分)画出求12-22+32-42+…+992-1002的值的程序框图.
答案
一、选择题(每题5分,共60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
A
B
C
D
B
B
B
B
A
C
二、填空题(每题5分,共20分)
;
14.
120
;
24
;
16.
;
三、
17.解 由于男生从4人中任意选取,女生从3人中任意选取,为了得到试验的全部结果,我们设男生为A,B,C,D,女生为1,2,3,我们可以用一个“数对”来表示随机选取的结果.如(A,1)表示:从男生中随机选取的是男生A,从女生中选取的是女生1,可用列举法列出所有可能的结果.如下表所示,设“国家一级运动员参赛”为事件E.
1
2
3
A
(A,1)
(A,2)
(A,3)
B
(B,1)
(B,2)
(B,3)
C
(C,1)
(C,2)
(C,3)
D
(D,1)
(D,2)
(D,3)
由上表可知,可能的结果总数是12个.设该国家一级运动员为编号1,她参赛的可能事件有4个,故她参赛的概率为P(E)==.
18.解 (1)对任一人,其血型为A、B、AB、O型血的事件分别记为A′、B′、C′、D′,它们是互斥的.由已知,有
P(A′)=0.28,P(B′)=0.29,P(C′)=0.08,P(D′)=0.35.
因为B、O型血可以输给B型血的人,故“可以输给B型血的人”为事件B′∪D′.根据互斥事件的加法公式,有
P(B′∪D′)=P(B′)+P(D′)=0.29+0.35=0.64.
(2)由于A、AB型血不能输给B型血的人,故“不能输给B型血的人”为事件A′∪C′,且P(A′∪C′)=P(A′)+P(C′)=0.28+0.08=0.36.
答 任找一人,其血可以输给小明的概率为0.64,其血不能输给小明的概率为0.36.
19.解 程序为:
INPUT
x IF
x>0
THEN y=2
x^2-1
ELSE
IF
x=0
THEN
y=2
x+1
ELSE
y=-2
x^2+4
END
IF
END
IF
y
END
20.解 (1)有两处错误:
①语句i=1应为i=2.
②语句LOOP
UNTIL
i>=99应为LOOP
UNTIL
i>99
(2)改为WHILE型循环语句
21.答案.
解析
如图所示
P==.
22.答案。
女
结
果
男
同课章节目录
