八年级数学上册函数及一次函数有关内容讲学案
文档属性
| 名称 | 八年级数学上册函数及一次函数有关内容讲学案 |  | |
| 格式 | zip | ||
| 文件大小 | 162.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-29 15:16:40 | ||
图片预览


文档简介
函数及一次函数有关内容
【本讲教育信息】
一.
教学内容:
函数及一次函数有关内容
学习目标:
1.
理解常量、变量以及函数的概念,知道函数的三种表示方法;
2.
掌握一次函数y=kx+b和正比例函数y=kx的概念、它们之间的关系以及会用待定系数法求这两个函数的关系式;
3.
能通过图形、表格等搜集信息并处理信息,学会表达思想.
二.
重点、难点:
1.
函数、一次函数、正比例函数的概念,函数的三种表示方法、待定系数法、识图等能力是重点;
2.
函数概念的理解是难点.
三.
知识要点:
1.
函数:
一般地,如果在一个变化的过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有惟一的值与它对应,那么我们称y是x的函数.其中,x是自变量,y是因变量.
2.
函数的三种表示方法:
表格法,图像法,关系式法
3.
一次函数与正比例函数:
(1)一次函数:一般地,如果两个变量x与y之间的函数关系可以写成y=kx+b(k,b为常数,且k≠0)的形式,那么称y是x的一次函数.需要注意的是:k≠0;
(2)正比例函数:若一次函数y=kx+b中的b=0,则一次函数变为:y=kx,这时我们称y是x的正比例函数.正比例函数是一次函数的特例.
4.
待定系数法:
【典型例题】
例1.
下列问题中的两个变量是否是函数关系
(1)一个正方形的边长是3cm,它的边长减少x
cm后,得到的新正方形的周长是y
cm,y可以看成是x的函数吗
(2)y是x的倒数,y是x的函数吗
(3)某人的身高是他本人年龄的函数吗
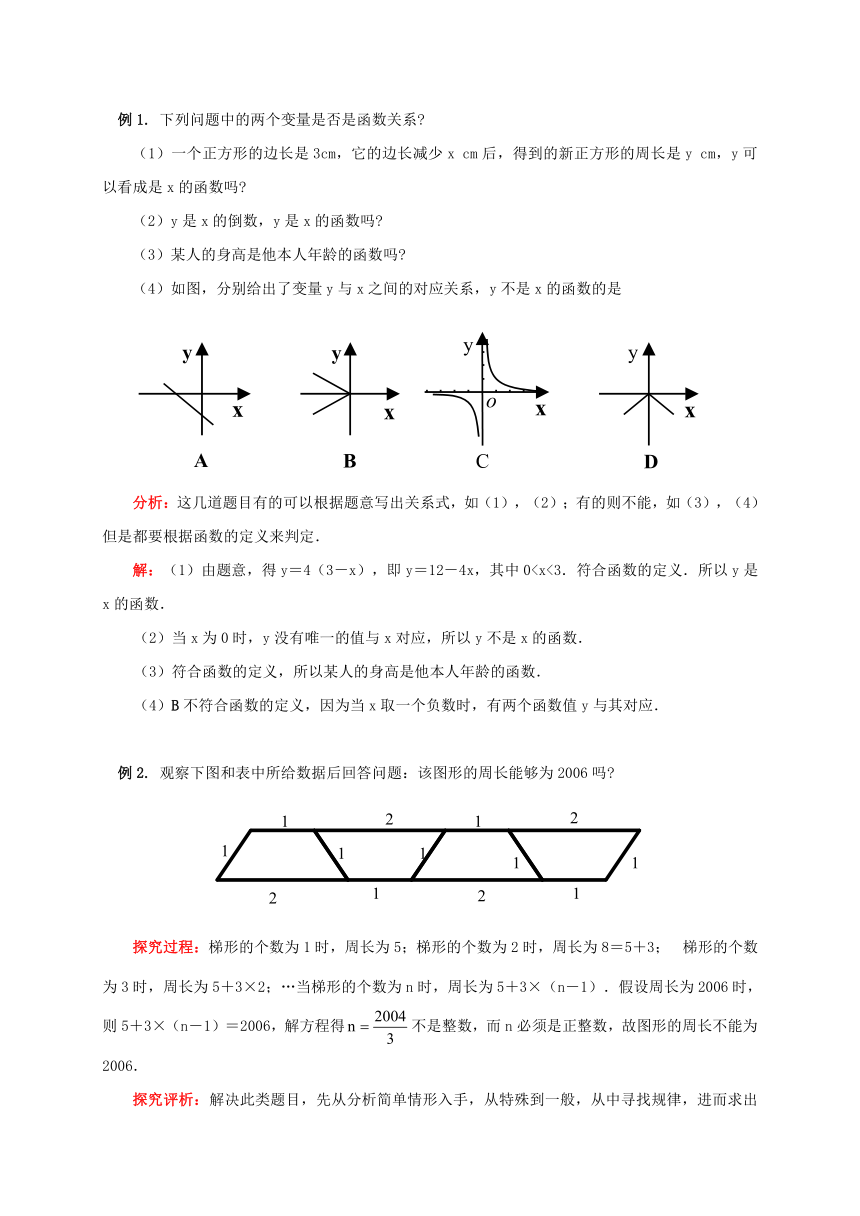
(4)如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是
分析:这几道题目有的可以根据题意写出关系式,如(1),(2);有的则不能,如(3),(4)但是都要根据函数的定义来判定.
解:(1)由题意,得y=4(3-x),即y=12-4x,其中0(2)当x为0时,y没有唯一的值与x对应,所以y不是x的函数.
(3)符合函数的定义,所以某人的身高是他本人年龄的函数.
(4)B不符合函数的定义,因为当x取一个负数时,有两个函数值y与其对应.
例2.
观察下图和表中所给数据后回答问题:该图形的周长能够为2006吗
探究过程:梯形的个数为1时,周长为5;梯形的个数为2时,周长为8=5+3;梯形的个数为3时,周长为5+3×2;…当梯形的个数为n时,周长为5+3×(n-1).假设周长为2006时,则5+3×(n-1)=2006,解方程得不是整数,而n必须是正整数,故图形的周长不能为2006.
探究评析:解决此类题目,先从分析简单情形入手,从特殊到一般,从中寻找规律,进而求出两个变量之间的函数关系式,继而由自变量求函数值,或由函数值求自变量的值.本题就是求自变量的值.
例3.
仔细观察下图,回答下列问题:
(1)图中反映的是哪两个变量之间的关系
(2)A,B两点分别代表什么
(3)说一说速度是怎样随时间变化的
分析:本题用图形的形式反映了两个变量:速度与时间,即速度随时间变化的情况.
解:(1)图中反映的是速度随时间变化的情况;
(2)点A表示第9分钟时速度是20km/h;点B表示第15分钟时速度是0
km/h;
(3)从开始到第3分钟,速度从0
km/h增加到20
km/h;第3分钟到第9分钟,速度保持20
km/h;第9分钟到第12分钟,速度从20
km/h增加到60
km/h;第12分钟到15分钟,速度从60
km/h降低到0
km/h.
例4.
当m,n为何值时,函数
(1)是一次函数 (2)是正比例函数
分析:根据一次函数及正比例函数的标准形式,我们就可以得出相关的方程(组),求出m,n的值
解:(1)由题意得,
故当时,该函数为一次函数.
(2)由题意得,
故当时,该函数为正比例函数.
例5.
为了保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度.
第一套
第二套
椅子高度x/cm
40.0
37.0
桌子高度y/cm
75.0
70.2
(1)请确定y与x的函数关系式.
(2)现有一把高度为39cm的椅子和一张高度为78.2cm的课桌,它们是否配套 为什么
分析:解答本题的关键是将实际问题抽象成数学问题,既考查了用待定系数法求函数关系式,又考查了函数对应值的知识.求解时要认真审题,准确理解配套的意义.
解:(1)设y与x的函数关系式为.
由表格可知,当x=40.0时,y=75.0;当x=37.0时,y=70.2.
所以
所以,y与x的函数关系式为
(2)当椅子高度为x=39cm时,相配套的桌子的高度应为
.
所以,一把高度为39cm的椅子和一张高度为78.2cm的课桌不配套.
【模拟试题】(答题时间:45分钟)
1.
池中有水600m3,每小时抽出50
m3,则池中剩余水量Q与时间t的函数关系式
;
2.
一蜡烛长20cm,点燃后每小时燃烧5cm,剩余高度l(cm)与燃烧时间t(h)的函数关系式
;
3.
已知等腰三角形的面积为20cm2,底上的高h(cm)与底边为x(cm)之间的函数关系式
;
4.
某新生办理月票卡时一次存入50元,每次乘车刷卡扣费0.5元,则卡内剩余金额y(元)与刷卡次数x的关系式为
;
5.
一根弹簧原长18cm,挂重不超过24kg时,每增加1kg,弹簧就拉长0.5cm,弹簧的长度y(cm)与所挂物重x(kg)之间的函数关系式
;
6.
某公司业务员到A市出差,,打车从火车站到分公司的车费,起步价为8元(3km以内),超过3km每增加1km加收2.4元(不足1km按1km计算),车费P(元)与路程x(km)之间的函数关系式
;
7.
某移动公司为用户提供两种资费方式拨打市话.甲:拨打和接听市话0.20元/min,但每月要交10元月租费;乙:拨打和接听市话0.40元/min,不收月租费.甲,乙两种方式下的费用y1,y2(元)与拨打或接听电话时间t(min)之间的关系式
;
8.
某市民用电收费标准为每千瓦时0.52元,电费y(元)与用电千瓦时数x(千瓦时)之间的关系式
;
9.
某市电力公司为了鼓励居民用电,采用分段计费的方法计算电费:每月用电量不超过100千瓦时时,按每千瓦时0.57元计费;每月用电量超过100千瓦时时,其中的100千瓦时仍按原标准收费,超过部分按每千瓦时0.50元计费.设月用电x千瓦时时,应交电费y元,当0≤x≤100时,
y=
,当x>100时,y=
10.
“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则图中与故事情节相吻合的是(
)
11.
小刚和他的爸爸、爷爷同时从家中出发到达同一个目的地后都立即返回,小刚去时骑自行车,返回时步行;爷爷去时步行,返回时骑自行车;爸爸往返都步行,三人步行的速度不等,小刚与爷爷的骑车的速度相等,每个人的行走路程S与时间t的关系分别是图中三个图象中的一个.走完一个往返,小刚用了
分钟;爷爷用了
分钟;爸爸用了
分钟.
12.
随着海峡两岸交流日益增强,通过“零关税”进入我市的一种台湾水果,其进货成本是每吨0.5万元,这种水果市场上的销售量y(吨)是每吨的销售价x(万元)的一次函数,且当x=0.6时,y=2.4;当x=1时,y=2.
(1)求出销售量y(吨)与每吨的销售价x(万元)之间的函数关系式;
(2)若销售利润为(万元),写出与x之间的函数关系式.
13.
地表以下岩层的温度y(℃)随着所处的深度x变化而变化,在一定范围内,y可以近似地看作是x的一次函数,并且当岩层所处深度是7km和10km时,它的温度分别是263℃和370℃,求这个函数的关系式.
【试题答案】
1.
Q
=600-50t
2.
l=20-5t
3.
4.
y=50-0.5x
5.
y=18+0.5x(0≤x≤24)
6.
7.
8.
y=0.52x
9.
y=0.57x,y=57+0.5(x-100)
10.
D
11.
21,26,24
12.
(1)y=-x+3,(2)ω=-x2+3.5x-1.5
13.
【本讲教育信息】
一.
教学内容:
函数及一次函数有关内容
学习目标:
1.
理解常量、变量以及函数的概念,知道函数的三种表示方法;
2.
掌握一次函数y=kx+b和正比例函数y=kx的概念、它们之间的关系以及会用待定系数法求这两个函数的关系式;
3.
能通过图形、表格等搜集信息并处理信息,学会表达思想.
二.
重点、难点:
1.
函数、一次函数、正比例函数的概念,函数的三种表示方法、待定系数法、识图等能力是重点;
2.
函数概念的理解是难点.
三.
知识要点:
1.
函数:
一般地,如果在一个变化的过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有惟一的值与它对应,那么我们称y是x的函数.其中,x是自变量,y是因变量.
2.
函数的三种表示方法:
表格法,图像法,关系式法
3.
一次函数与正比例函数:
(1)一次函数:一般地,如果两个变量x与y之间的函数关系可以写成y=kx+b(k,b为常数,且k≠0)的形式,那么称y是x的一次函数.需要注意的是:k≠0;
(2)正比例函数:若一次函数y=kx+b中的b=0,则一次函数变为:y=kx,这时我们称y是x的正比例函数.正比例函数是一次函数的特例.
4.
待定系数法:
【典型例题】
例1.
下列问题中的两个变量是否是函数关系
(1)一个正方形的边长是3cm,它的边长减少x
cm后,得到的新正方形的周长是y
cm,y可以看成是x的函数吗
(2)y是x的倒数,y是x的函数吗
(3)某人的身高是他本人年龄的函数吗
(4)如图,分别给出了变量y与x之间的对应关系,y不是x的函数的是
分析:这几道题目有的可以根据题意写出关系式,如(1),(2);有的则不能,如(3),(4)但是都要根据函数的定义来判定.
解:(1)由题意,得y=4(3-x),即y=12-4x,其中0
(3)符合函数的定义,所以某人的身高是他本人年龄的函数.
(4)B不符合函数的定义,因为当x取一个负数时,有两个函数值y与其对应.
例2.
观察下图和表中所给数据后回答问题:该图形的周长能够为2006吗
探究过程:梯形的个数为1时,周长为5;梯形的个数为2时,周长为8=5+3;梯形的个数为3时,周长为5+3×2;…当梯形的个数为n时,周长为5+3×(n-1).假设周长为2006时,则5+3×(n-1)=2006,解方程得不是整数,而n必须是正整数,故图形的周长不能为2006.
探究评析:解决此类题目,先从分析简单情形入手,从特殊到一般,从中寻找规律,进而求出两个变量之间的函数关系式,继而由自变量求函数值,或由函数值求自变量的值.本题就是求自变量的值.
例3.
仔细观察下图,回答下列问题:
(1)图中反映的是哪两个变量之间的关系
(2)A,B两点分别代表什么
(3)说一说速度是怎样随时间变化的
分析:本题用图形的形式反映了两个变量:速度与时间,即速度随时间变化的情况.
解:(1)图中反映的是速度随时间变化的情况;
(2)点A表示第9分钟时速度是20km/h;点B表示第15分钟时速度是0
km/h;
(3)从开始到第3分钟,速度从0
km/h增加到20
km/h;第3分钟到第9分钟,速度保持20
km/h;第9分钟到第12分钟,速度从20
km/h增加到60
km/h;第12分钟到15分钟,速度从60
km/h降低到0
km/h.
例4.
当m,n为何值时,函数
(1)是一次函数 (2)是正比例函数
分析:根据一次函数及正比例函数的标准形式,我们就可以得出相关的方程(组),求出m,n的值
解:(1)由题意得,
故当时,该函数为一次函数.
(2)由题意得,
故当时,该函数为正比例函数.
例5.
为了保护学生视力,课桌椅的高度都是按一定的关系配套设计的,研究表明:假设课桌的高度为ycm,椅子的高度为xcm,则y应是x的一次函数,下表列出两套符合条件的课桌椅的高度.
第一套
第二套
椅子高度x/cm
40.0
37.0
桌子高度y/cm
75.0
70.2
(1)请确定y与x的函数关系式.
(2)现有一把高度为39cm的椅子和一张高度为78.2cm的课桌,它们是否配套 为什么
分析:解答本题的关键是将实际问题抽象成数学问题,既考查了用待定系数法求函数关系式,又考查了函数对应值的知识.求解时要认真审题,准确理解配套的意义.
解:(1)设y与x的函数关系式为.
由表格可知,当x=40.0时,y=75.0;当x=37.0时,y=70.2.
所以
所以,y与x的函数关系式为
(2)当椅子高度为x=39cm时,相配套的桌子的高度应为
.
所以,一把高度为39cm的椅子和一张高度为78.2cm的课桌不配套.
【模拟试题】(答题时间:45分钟)
1.
池中有水600m3,每小时抽出50
m3,则池中剩余水量Q与时间t的函数关系式
;
2.
一蜡烛长20cm,点燃后每小时燃烧5cm,剩余高度l(cm)与燃烧时间t(h)的函数关系式
;
3.
已知等腰三角形的面积为20cm2,底上的高h(cm)与底边为x(cm)之间的函数关系式
;
4.
某新生办理月票卡时一次存入50元,每次乘车刷卡扣费0.5元,则卡内剩余金额y(元)与刷卡次数x的关系式为
;
5.
一根弹簧原长18cm,挂重不超过24kg时,每增加1kg,弹簧就拉长0.5cm,弹簧的长度y(cm)与所挂物重x(kg)之间的函数关系式
;
6.
某公司业务员到A市出差,,打车从火车站到分公司的车费,起步价为8元(3km以内),超过3km每增加1km加收2.4元(不足1km按1km计算),车费P(元)与路程x(km)之间的函数关系式
;
7.
某移动公司为用户提供两种资费方式拨打市话.甲:拨打和接听市话0.20元/min,但每月要交10元月租费;乙:拨打和接听市话0.40元/min,不收月租费.甲,乙两种方式下的费用y1,y2(元)与拨打或接听电话时间t(min)之间的关系式
;
8.
某市民用电收费标准为每千瓦时0.52元,电费y(元)与用电千瓦时数x(千瓦时)之间的关系式
;
9.
某市电力公司为了鼓励居民用电,采用分段计费的方法计算电费:每月用电量不超过100千瓦时时,按每千瓦时0.57元计费;每月用电量超过100千瓦时时,其中的100千瓦时仍按原标准收费,超过部分按每千瓦时0.50元计费.设月用电x千瓦时时,应交电费y元,当0≤x≤100时,
y=
,当x>100时,y=
10.
“龟兔赛跑”讲述了这样的故事:领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉.当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点.用S1、S2分别表示乌龟和兔子所行的路程,t为时间,则图中与故事情节相吻合的是(
)
11.
小刚和他的爸爸、爷爷同时从家中出发到达同一个目的地后都立即返回,小刚去时骑自行车,返回时步行;爷爷去时步行,返回时骑自行车;爸爸往返都步行,三人步行的速度不等,小刚与爷爷的骑车的速度相等,每个人的行走路程S与时间t的关系分别是图中三个图象中的一个.走完一个往返,小刚用了
分钟;爷爷用了
分钟;爸爸用了
分钟.
12.
随着海峡两岸交流日益增强,通过“零关税”进入我市的一种台湾水果,其进货成本是每吨0.5万元,这种水果市场上的销售量y(吨)是每吨的销售价x(万元)的一次函数,且当x=0.6时,y=2.4;当x=1时,y=2.
(1)求出销售量y(吨)与每吨的销售价x(万元)之间的函数关系式;
(2)若销售利润为(万元),写出与x之间的函数关系式.
13.
地表以下岩层的温度y(℃)随着所处的深度x变化而变化,在一定范围内,y可以近似地看作是x的一次函数,并且当岩层所处深度是7km和10km时,它的温度分别是263℃和370℃,求这个函数的关系式.
【试题答案】
1.
Q
=600-50t
2.
l=20-5t
3.
4.
y=50-0.5x
5.
y=18+0.5x(0≤x≤24)
6.
7.
8.
y=0.52x
9.
y=0.57x,y=57+0.5(x-100)
10.
D
11.
21,26,24
12.
(1)y=-x+3,(2)ω=-x2+3.5x-1.5
13.
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
