八年级数学上册第五章平面直角坐标系讲学案
文档属性
| 名称 | 八年级数学上册第五章平面直角坐标系讲学案 |  | |
| 格式 | zip | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-29 15:19:09 | ||
图片预览


文档简介
平面直角坐标系
【本讲教育信息】
一.
教学内容:
平面直角坐标系
[目标]
1.
认识平面直角坐标系,知道点的坐标及象限的含义.
2.
能够在给定的直角坐标系中,根据点的坐标指出点的位置,会由点的位置写出点的坐标.
3.
掌握对称点的坐标关系.
4.
理解点的坐标的数值变化与点的位置变化的关系.
二
知识要点:
1.
平面上有____且互相__的2条数轴构成平面直角坐标系.水平方向的数轴称为___,竖直方向的数轴称为___,公共原点称为___.写出某点的坐标时,___应写在____的前面.
2.
各象限点的符号特征:
象限
第一
第二
第三
第四
符号
(+,+)
x轴上的点,__坐标为0
y轴上的点,__坐标为0
3.
点的坐标特征:
(1)平行于坐标轴的直线上的点:平行于x轴的直线上不同的两个点的__坐标相同,__坐标不同;平行于y轴的直线上不同的两个点的__坐标相同,__坐标不同.
(2)象限角平分线上的点:第一、三象限角平分线上的点的横、纵坐标___,可表示为(x,x);第二、四象限角平分线上的点的横、纵坐标_____,可表示为( ).
(3)对称的点P(a,b)
关于x轴对称的点的坐标为( , ),
关于y轴对称的点的坐标为( , ),关于原点对称的点的坐标为( , )
4.
图形变换后点的坐标特征:
图形左右平移,对应点的__坐标变化,__坐标不变;图形上下平移,对应点的__坐标变化,__坐标不变
【典型例题】
例1.
已知平面直角坐标系中两点A(x,1)、B(-5,y)
(1)若点A、B关于x轴对称,则x=____,y=____;
(2)若点A、B关于y轴对称,则x=____,y=_____;
(3)若点A、B关于原点对称,则x=____,y=_____.
答案:略
例2.
已知点P(2m一5,m一1),当m为何值时:
(1)点P在二、四象限的角平分线上;
(2)点P在一、三象限的角平分线上.
答案:略
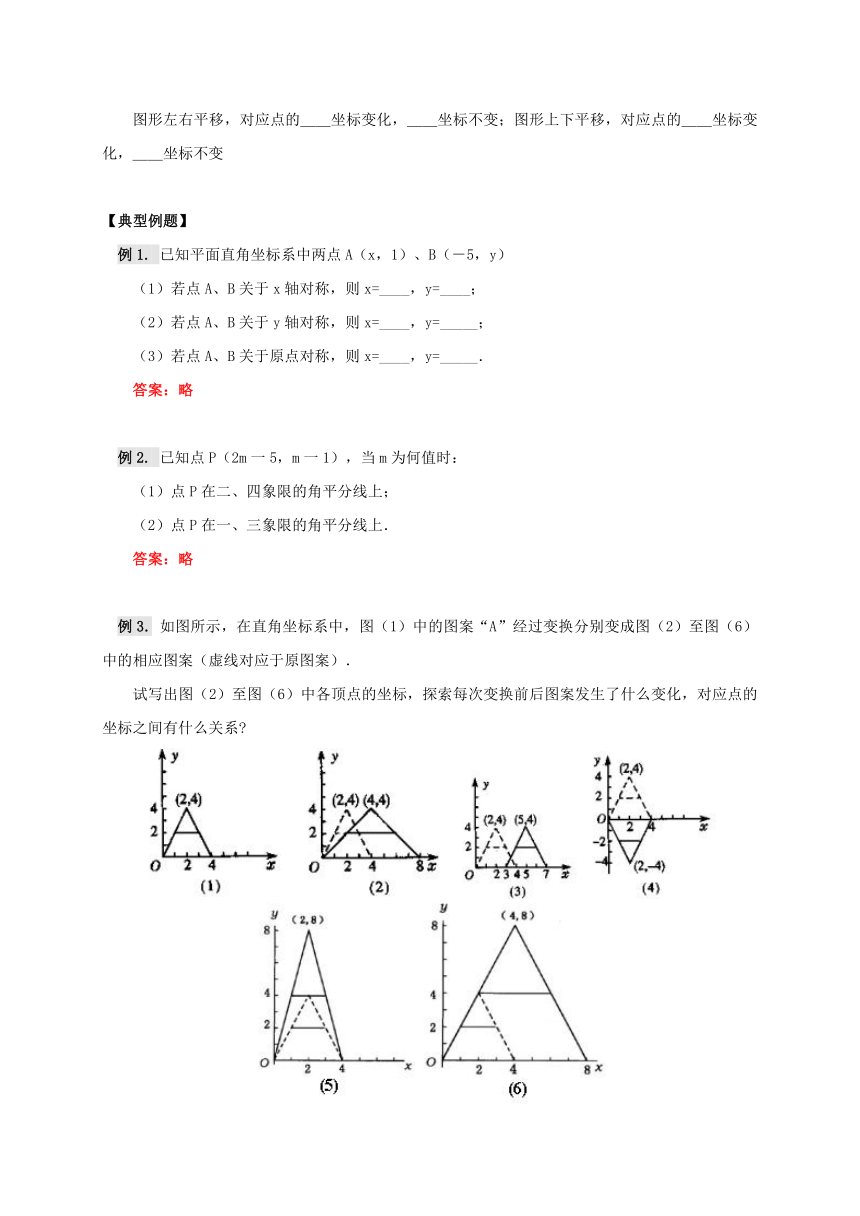
例3.
如图所示,在直角坐标系中,图(1)中的图案“A”经过变换分别变成图(2)至图(6)中的相应图案(虚线对应于原图案).
试写出图(2)至图(6)中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系
答案:略
例4.
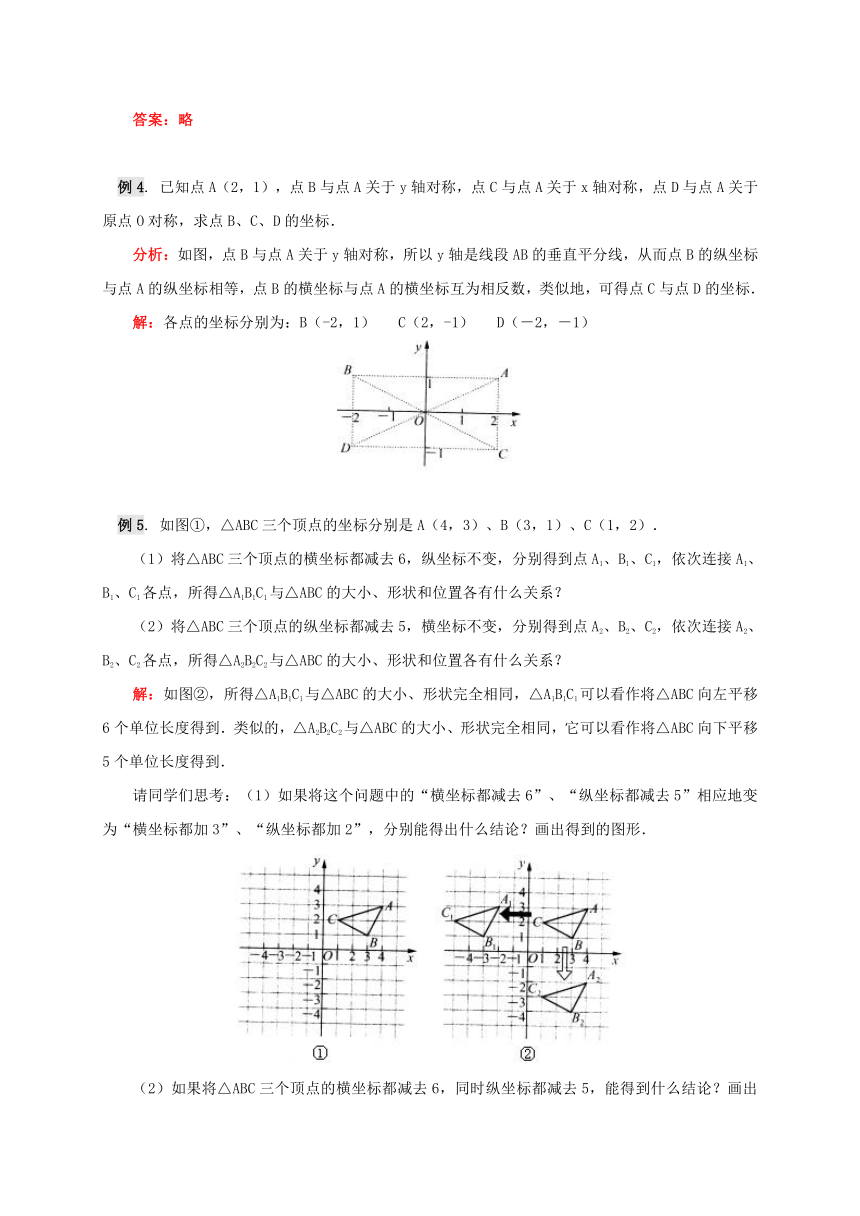
已知点A(2,1),点B与点A关于y轴对称,点C与点A关于x轴对称,点D与点A关于原点O对称,求点B、C、D的坐标.
分析:如图,点B与点A关于y轴对称,所以y轴是线段AB的垂直平分线,从而点B的纵坐标与点A的纵坐标相等,点B的横坐标与点A的横坐标互为相反数,类似地,可得点C与点D的坐标.
解:各点的坐标分别为:B(-2,1)
C(2,-1)
D(-2,-1)
例5.
如图①,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接A1、B1、C1各点,所得△A1B1C1与△ABC的大小、形状和位置各有什么关系?
(2)将△ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2各点,所得△A2B2C2与△ABC的大小、形状和位置各有什么关系?
解:如图②,所得△A1B1C1与△ABC的大小、形状完全相同,△A1B1C1可以看作将△ABC向左平移6个单位长度得到.类似的,△A2B2C2与△ABC的大小、形状完全相同,它可以看作将△ABC向下平移5个单位长度得到.
请同学们思考:(1)如果将这个问题中的“横坐标都减去6”、“纵坐标都减去5”相应地变为“横坐标都加3”、“纵坐标都加2”,分别能得出什么结论?画出得到的图形.
(2)如果将△ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,能得到什么结论?画出得到的图形.
(3)在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减)一个正数a,相应的新图形就是把原图形向____________(或向_______)平移_________
个单位长度;如果把它各个点的纵坐标都加(或减)一个正数b,相应的新图形就是把原图形向________(或向___________)平移______个单位长度.
例6.
已知:点A(6,2)、B(2,-4),求S△AOB(O为坐标原点).
分析:解决这种图形的面积问题,需要认真挖掘图形特点,转化仍是解决问题的重要手段.
解:因为A(6,2)、B(2,-4).
过点A作AC⊥y轴,垂足为C,
过点B作BD⊥y轴,垂足为D,
所以AC=6,OC=2,BD=2,OD=4.
所以S△AOB=S直角梯形BACD-S△AOC-△BOD.
所以S△AOB=(2+6)×(2+4)×
-×6×2-×4×2=14
【模拟试题】(答题时间:40分钟)
一、选择题(每题3分,共30分)
1.
下列点中,位于直角坐标系第二象限的点是(
)
A.
(2,1)
B.
(-2,-1)
C.
(-2,1)
D.
(2,-1)
2.
在直角坐标系中,点A(3,1),点B(3,3),则线段AB的中点坐标是(
)
A.
(2,3)
B.
(3,2)
C.
(6,2)
D.
(6,4)
3.
在直角坐标系中,点A(2,0),点B(0,2),则线段AB的中点到原点的距离是(
)
A.
B.
1
C.
D.
2
4.
在直角坐标系中,点A(2,1)向左平移4个单位长度,再向下平移2个单位长度后的坐标为(
)
A.
(4,3)
B.
(-2,-1)
C.
(4,-1)
D.
(-2,3)
5.
若点P在第四象限,且到两条坐标轴的距离都是4,则点P的坐标为(
)
A.
(-4,4)
B.
(-4,-4)
C.
(4,-4)
D.
(4,4)
6.
点A(-4,-4)到原点的距离为(
)
A.
3
B.
4
C.
5
D.
7.
点A(-2,-3)和点B(2,3)在直角坐标系中(
)
A.
关于x轴对称
B.
关于y轴对称
C.
关于原点对称
D.
不关于坐标轴和原点对称
8.
一辆汽车行驶的路程与行驶时间的关系如图所示.下列说法正确的是(
)
A.
前3h中汽车的速度越来越快
B.
3h后汽车静止不动
C.
3h后汽车以相同的速度行驶
D.
前3h汽车以相同速度行驶
9.
如图,直角坐标系中,正方形ABCD的面积是(
)
A.
1
B.
2
C.
4
D.
10.
若xy>0,则点(x,y)在直角坐标系中位于(
)
A.
x轴上
B.
y轴上
C.
第一或第三象限
D.
第二或第四象限
二、填空题(每空2分,共16分)
11.
在直角坐标系中,点A(-3,m)与点B(n,1)关于x轴对称,则m=________,n=________.
12.
点P(a+1,a-1)在直角坐标系的y轴上,则点P坐标为________.
13.
在直角坐标系中,点A(x,y),且.试写出两个满足这些条件的点:________.
14.
在直角坐标系中,点A(-1,1),将线段OA(O为坐标原点)绕点O逆时针旋转得线段OB,则点B的坐标是________.
15.
点P(a,3)到y轴的距离为4,则a的值为________.
16.
在直角坐标系中,点A(0,2),点P(x,0)为x轴上的一个动点,当x=________时,线段PA的长得到最小值,最小值是________.
三、解答题(第17题、18题各9分,第19、20、21题各12分,共54分)
17.
下表记录的是某市某天一昼夜温度变化的数据:
时刻/时
0
2
4
6
8
10
12
14
16
18
20
22
24
温度/℃
-3
-5
-6.5
-4
0
4
7.5
10
8
5
1
-1
-2
请根据表格数据回答下列问题:
(1)早晨6时和中午12时的气温各是多少度?
(2)这一天的温差是多少度?
(3)这一天内温度上升的时段是几时至几时?
18.
已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为5.试求点N的坐标.
19.
如图,Rt△ABC中,∠C=90°,AC=BC,AB=4,试建立适当的直角坐标系,写出各顶点的坐标.
20.
在同一直角坐标系中分别描出点A(-3,0)、B(2,0)、C(1,3),再用线段将这三点首尾顺次连接起来.求△ABC的面积与周长.
21.
在平面直角坐标系中,分别描出点A(-1,0),B(0,2),C(1,0),D(0,-2).
(1)试判断四边形ABCD的形状;
(2)若B、D两点不动,你能通过变动点A、C的位置使四边形ABCD成为正方形吗?若能,请写出变动后的点A、C的坐标.
【试题答案】
一、选择题
1.C
2.B
3.C
4.B
5.C
6.D
7.C
8.B
9.B
10.C
二、填空题
11.
-1,-3
12.(0,-2)
13.
答案不限
14.
(0,-)
15.±
4
16.
0,
2
三、解答题
17.
(1)-4℃,7.5℃
(2)16.5℃
(3)4点-14点
18.
N
(±5,
2)
19.
答案不限
20.
S△ABC=7.5
C△ABC=+10
21.(1)菱形
(2)A(-2,
0)
C(2,
0)
【本讲教育信息】
一.
教学内容:
平面直角坐标系
[目标]
1.
认识平面直角坐标系,知道点的坐标及象限的含义.
2.
能够在给定的直角坐标系中,根据点的坐标指出点的位置,会由点的位置写出点的坐标.
3.
掌握对称点的坐标关系.
4.
理解点的坐标的数值变化与点的位置变化的关系.
二
知识要点:
1.
平面上有____且互相__的2条数轴构成平面直角坐标系.水平方向的数轴称为___,竖直方向的数轴称为___,公共原点称为___.写出某点的坐标时,___应写在____的前面.
2.
各象限点的符号特征:
象限
第一
第二
第三
第四
符号
(+,+)
x轴上的点,__坐标为0
y轴上的点,__坐标为0
3.
点的坐标特征:
(1)平行于坐标轴的直线上的点:平行于x轴的直线上不同的两个点的__坐标相同,__坐标不同;平行于y轴的直线上不同的两个点的__坐标相同,__坐标不同.
(2)象限角平分线上的点:第一、三象限角平分线上的点的横、纵坐标___,可表示为(x,x);第二、四象限角平分线上的点的横、纵坐标_____,可表示为( ).
(3)对称的点P(a,b)
关于x轴对称的点的坐标为( , ),
关于y轴对称的点的坐标为( , ),关于原点对称的点的坐标为( , )
4.
图形变换后点的坐标特征:
图形左右平移,对应点的__坐标变化,__坐标不变;图形上下平移,对应点的__坐标变化,__坐标不变
【典型例题】
例1.
已知平面直角坐标系中两点A(x,1)、B(-5,y)
(1)若点A、B关于x轴对称,则x=____,y=____;
(2)若点A、B关于y轴对称,则x=____,y=_____;
(3)若点A、B关于原点对称,则x=____,y=_____.
答案:略
例2.
已知点P(2m一5,m一1),当m为何值时:
(1)点P在二、四象限的角平分线上;
(2)点P在一、三象限的角平分线上.
答案:略
例3.
如图所示,在直角坐标系中,图(1)中的图案“A”经过变换分别变成图(2)至图(6)中的相应图案(虚线对应于原图案).
试写出图(2)至图(6)中各顶点的坐标,探索每次变换前后图案发生了什么变化,对应点的坐标之间有什么关系
答案:略
例4.
已知点A(2,1),点B与点A关于y轴对称,点C与点A关于x轴对称,点D与点A关于原点O对称,求点B、C、D的坐标.
分析:如图,点B与点A关于y轴对称,所以y轴是线段AB的垂直平分线,从而点B的纵坐标与点A的纵坐标相等,点B的横坐标与点A的横坐标互为相反数,类似地,可得点C与点D的坐标.
解:各点的坐标分别为:B(-2,1)
C(2,-1)
D(-2,-1)
例5.
如图①,△ABC三个顶点的坐标分别是A(4,3)、B(3,1)、C(1,2).
(1)将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1、B1、C1,依次连接A1、B1、C1各点,所得△A1B1C1与△ABC的大小、形状和位置各有什么关系?
(2)将△ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2、B2、C2,依次连接A2、B2、C2各点,所得△A2B2C2与△ABC的大小、形状和位置各有什么关系?
解:如图②,所得△A1B1C1与△ABC的大小、形状完全相同,△A1B1C1可以看作将△ABC向左平移6个单位长度得到.类似的,△A2B2C2与△ABC的大小、形状完全相同,它可以看作将△ABC向下平移5个单位长度得到.
请同学们思考:(1)如果将这个问题中的“横坐标都减去6”、“纵坐标都减去5”相应地变为“横坐标都加3”、“纵坐标都加2”,分别能得出什么结论?画出得到的图形.
(2)如果将△ABC三个顶点的横坐标都减去6,同时纵坐标都减去5,能得到什么结论?画出得到的图形.
(3)在平面直角坐标系内,如果把一个图形各个点的横坐标都加(或减)一个正数a,相应的新图形就是把原图形向____________(或向_______)平移_________
个单位长度;如果把它各个点的纵坐标都加(或减)一个正数b,相应的新图形就是把原图形向________(或向___________)平移______个单位长度.
例6.
已知:点A(6,2)、B(2,-4),求S△AOB(O为坐标原点).
分析:解决这种图形的面积问题,需要认真挖掘图形特点,转化仍是解决问题的重要手段.
解:因为A(6,2)、B(2,-4).
过点A作AC⊥y轴,垂足为C,
过点B作BD⊥y轴,垂足为D,
所以AC=6,OC=2,BD=2,OD=4.
所以S△AOB=S直角梯形BACD-S△AOC-△BOD.
所以S△AOB=(2+6)×(2+4)×
-×6×2-×4×2=14
【模拟试题】(答题时间:40分钟)
一、选择题(每题3分,共30分)
1.
下列点中,位于直角坐标系第二象限的点是(
)
A.
(2,1)
B.
(-2,-1)
C.
(-2,1)
D.
(2,-1)
2.
在直角坐标系中,点A(3,1),点B(3,3),则线段AB的中点坐标是(
)
A.
(2,3)
B.
(3,2)
C.
(6,2)
D.
(6,4)
3.
在直角坐标系中,点A(2,0),点B(0,2),则线段AB的中点到原点的距离是(
)
A.
B.
1
C.
D.
2
4.
在直角坐标系中,点A(2,1)向左平移4个单位长度,再向下平移2个单位长度后的坐标为(
)
A.
(4,3)
B.
(-2,-1)
C.
(4,-1)
D.
(-2,3)
5.
若点P在第四象限,且到两条坐标轴的距离都是4,则点P的坐标为(
)
A.
(-4,4)
B.
(-4,-4)
C.
(4,-4)
D.
(4,4)
6.
点A(-4,-4)到原点的距离为(
)
A.
3
B.
4
C.
5
D.
7.
点A(-2,-3)和点B(2,3)在直角坐标系中(
)
A.
关于x轴对称
B.
关于y轴对称
C.
关于原点对称
D.
不关于坐标轴和原点对称
8.
一辆汽车行驶的路程与行驶时间的关系如图所示.下列说法正确的是(
)
A.
前3h中汽车的速度越来越快
B.
3h后汽车静止不动
C.
3h后汽车以相同的速度行驶
D.
前3h汽车以相同速度行驶
9.
如图,直角坐标系中,正方形ABCD的面积是(
)
A.
1
B.
2
C.
4
D.
10.
若xy>0,则点(x,y)在直角坐标系中位于(
)
A.
x轴上
B.
y轴上
C.
第一或第三象限
D.
第二或第四象限
二、填空题(每空2分,共16分)
11.
在直角坐标系中,点A(-3,m)与点B(n,1)关于x轴对称,则m=________,n=________.
12.
点P(a+1,a-1)在直角坐标系的y轴上,则点P坐标为________.
13.
在直角坐标系中,点A(x,y),且.试写出两个满足这些条件的点:________.
14.
在直角坐标系中,点A(-1,1),将线段OA(O为坐标原点)绕点O逆时针旋转得线段OB,则点B的坐标是________.
15.
点P(a,3)到y轴的距离为4,则a的值为________.
16.
在直角坐标系中,点A(0,2),点P(x,0)为x轴上的一个动点,当x=________时,线段PA的长得到最小值,最小值是________.
三、解答题(第17题、18题各9分,第19、20、21题各12分,共54分)
17.
下表记录的是某市某天一昼夜温度变化的数据:
时刻/时
0
2
4
6
8
10
12
14
16
18
20
22
24
温度/℃
-3
-5
-6.5
-4
0
4
7.5
10
8
5
1
-1
-2
请根据表格数据回答下列问题:
(1)早晨6时和中午12时的气温各是多少度?
(2)这一天的温差是多少度?
(3)这一天内温度上升的时段是几时至几时?
18.
已知点M(3,2)与点N(x,y)在同一条平行于x轴的直线上,且点N到y轴的距离为5.试求点N的坐标.
19.
如图,Rt△ABC中,∠C=90°,AC=BC,AB=4,试建立适当的直角坐标系,写出各顶点的坐标.
20.
在同一直角坐标系中分别描出点A(-3,0)、B(2,0)、C(1,3),再用线段将这三点首尾顺次连接起来.求△ABC的面积与周长.
21.
在平面直角坐标系中,分别描出点A(-1,0),B(0,2),C(1,0),D(0,-2).
(1)试判断四边形ABCD的形状;
(2)若B、D两点不动,你能通过变动点A、C的位置使四边形ABCD成为正方形吗?若能,请写出变动后的点A、C的坐标.
【试题答案】
一、选择题
1.C
2.B
3.C
4.B
5.C
6.D
7.C
8.B
9.B
10.C
二、填空题
11.
-1,-3
12.(0,-2)
13.
答案不限
14.
(0,-)
15.±
4
16.
0,
2
三、解答题
17.
(1)-4℃,7.5℃
(2)16.5℃
(3)4点-14点
18.
N
(±5,
2)
19.
答案不限
20.
S△ABC=7.5
C△ABC=+10
21.(1)菱形
(2)A(-2,
0)
C(2,
0)
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
