八年级数学上册一次函数的图像、性质和应用、二元一次方程组讲学案
文档属性
| 名称 | 八年级数学上册一次函数的图像、性质和应用、二元一次方程组讲学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 187.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-04-29 00:00:00 | ||
图片预览


文档简介
一次函数的图像、性质和应用;二元一次方程组
【本讲教育信息】
一.
教学内容:
一次函数的图像、性质和应用;二元一次方程组的图像解法
[学习目标]
1.
理解一次函数的图像是一条直线以及它的性质,会画一次函数的图像.
2.
会应用一次函数的性质解决实际问题,能够用图像法解二元一次方程组.
3.
通过学习,进一步体会“数形结合”的数学思想方法以及数学建模的思想.
二.
重点、难点:
能够熟练地用描点法、两点法画出一次函数的图像,用图像法解二元一次方程组,理解一次函数性质并会应用一次函数解决问题是重点;难点是对一次函数性质的理解以及应用一次函数解决问题.
三.
知识要点:
1.
一次函数与正比例函数的图像
一般地,一次函数的图像是过(),(0,b)的一条直线;特殊的,正比例函数的图像是过(0,0),(1,k)的一条直线.
直线是由直线向上或向下平移单位得到的.或者说直线是由直线向右或向左平移单位得到的.
2.
一次函数的性质
(1)增减性:如果,那么y的值随x值的增大而增大;
如果,那么y的值随x值的增大而减小
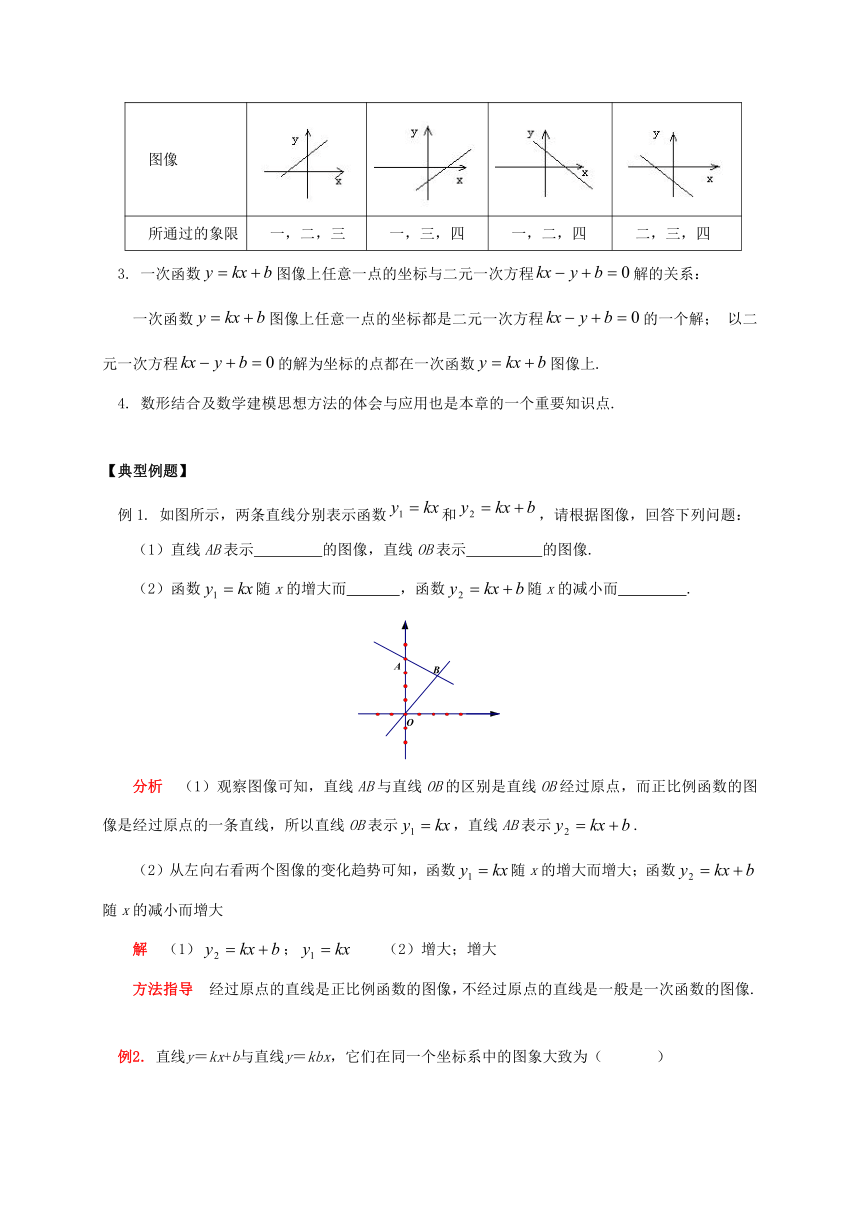
(2)所通过的象限如下表
k,b的符号
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
图像
所通过的象限
一,二,三
一,三,四
一,二,四
二,三,四
3.
一次函数图像上任意一点的坐标与二元一次方程解的关系:
一次函数图像上任意一点的坐标都是二元一次方程的一个解;
以二元一次方程的解为坐标的点都在一次函数图像上.
4.
数形结合及数学建模思想方法的体会与应用也是本章的一个重要知识点.
【典型例题】
例1.
如图所示,两条直线分别表示函数和,请根据图像,回答下列问题:
(1)直线AB表示
的图像,直线OB表示
的图像.
(2)函数随x的增大而
,函数随x的减小而
.
分析
(1)观察图像可知,直线AB与直线OB的区别是直线OB经过原点,而正比例函数的图像是经过原点的一条直线,所以直线OB表示,直线AB表示.
(2)从左向右看两个图像的变化趋势可知,函数随x的增大而增大;函数随x的减小而增大
解
(1);
(2)增大;增大
方法指导
经过原点的直线是正比例函数的图像,不经过原点的直线是一般是一次函数的图像.
例2.
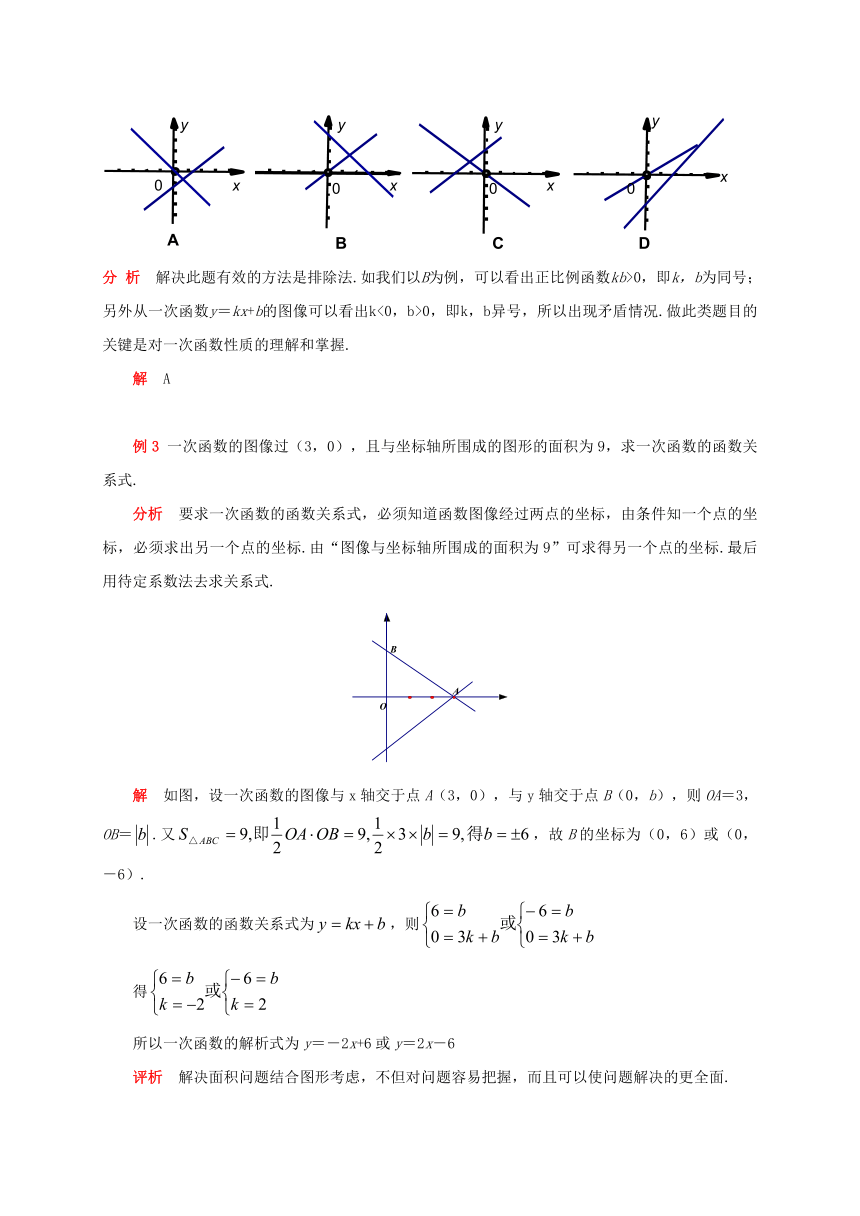
直线y=kx+b与直线y=kbx,它们在同一个坐标系中的图象大致为(
)
分
析
解决此题有效的方法是排除法.如我们以B为例,可以看出正比例函数kb>0,即k,b为同号;另外从一次函数y=kx+b的图像可以看出k<0,b>0,即k,b异号,所以出现矛盾情况.做此类题目的关键是对一次函数性质的理解和掌握.
解
A
例3
一次函数的图像过(3,0),且与坐标轴所围成的图形的面积为9,求一次函数的函数关系式.
分析
要求一次函数的函数关系式,必须知道函数图像经过两点的坐标,由条件知一个点的坐标,必须求出另一个点的坐标.由“图像与坐标轴所围成的面积为9”可求得另一个点的坐标.最后用待定系数法去求关系式.
解
如图,设一次函数的图像与x轴交于点A(3,0),与y轴交于点B(0,b),则OA=3,OB=.又,故B的坐标为(0,6)或(0,-6).
设一次函数的函数关系式为,则
得
所以一次函数的解析式为y=-2x+6或y=2x-6
评析
解决面积问题结合图形考虑,不但对问题容易把握,而且可以使问题解决的更全面.
例4
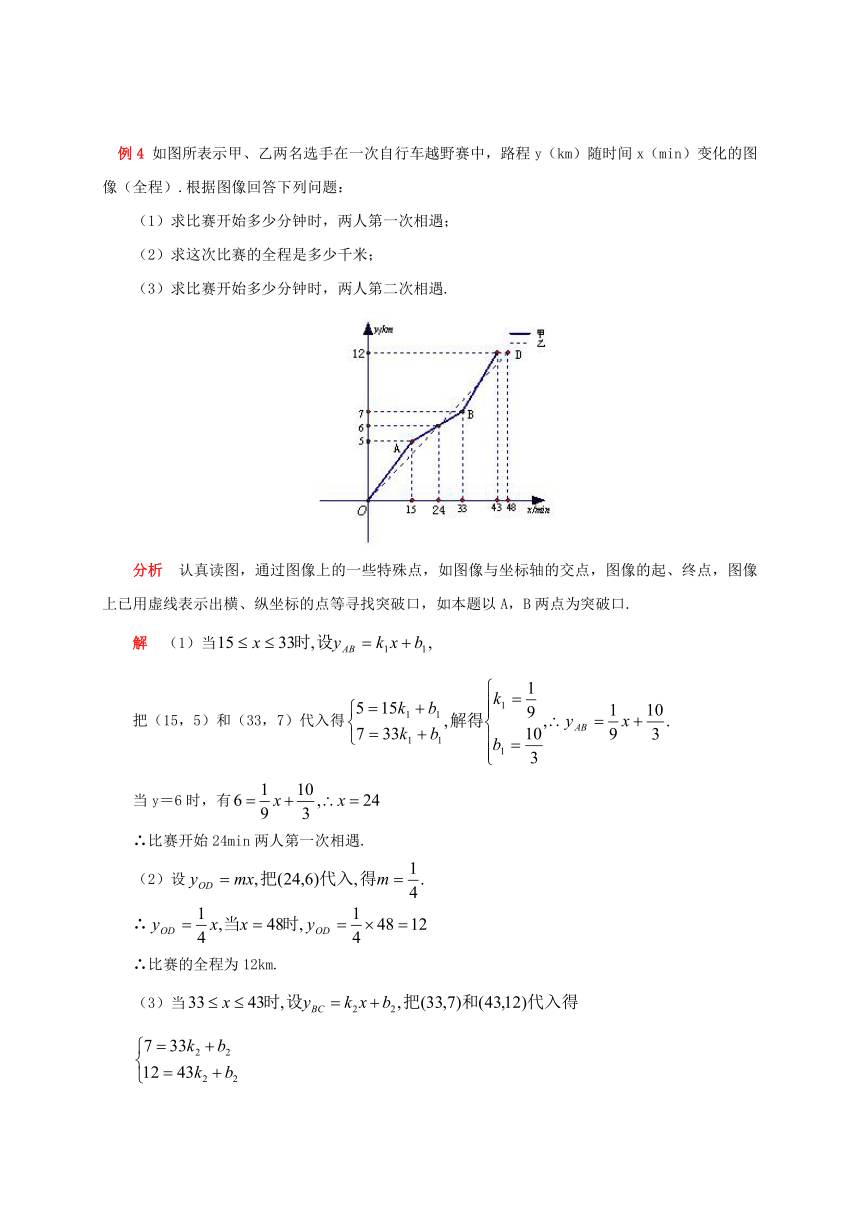
如图所表示甲、乙两名选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图像(全程).根据图像回答下列问题:
(1)求比赛开始多少分钟时,两人第一次相遇;
(2)求这次比赛的全程是多少千米;
(3)求比赛开始多少分钟时,两人第二次相遇.
分析
认真读图,通过图像上的一些特殊点,如图像与坐标轴的交点,图像的起、终点,图像上已用虚线表示出横、纵坐标的点等寻找突破口,如本题以A,B两点为突破口.
解
(1)当
把(15,5)和(33,7)代入得
当y=6时,有
∴比赛开始24min两人第一次相遇.
(2)设
∴
∴比赛的全程为12km.
(3)当
解得
解方程组
∴比赛开始38min两人第二次相遇.
评析
本题体现了从形到数的转化,是数形结合的具体运用,也是待定系数法的具体应用,此方法与方程、方程组的解法密不可分.
例5
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示.请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是
,从点燃到燃尽所用的时间分别是
;
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
分析
(1)纵轴表示蜡烛的高度.
(2)因为图像都是线段,所以它们的函数关系式都是一次函数.根据图像上提供的点的坐标用待定系数法分别求解.
(3)求出两条线段的交点坐标,结合图像的位置求解.
解
(1)30cm,
25cm;
2h,
2.5h
(2)设甲蜡烛燃烧时y与x函数关系式为
观察可知,它的图像经过点(2,0),
(0,30)
所以
解得
所以甲蜡烛燃烧时函数关系式为
设乙蜡烛燃烧时y与x函数关系式为
观察可知,它的图像经过点(2.5,0),
(0,25)
所以
解得
∴乙蜡烛燃烧时函数关系式为:
(3)当甲蜡烛与乙蜡烛的高度相等时,则
所以x=1时,甲蜡烛与乙蜡烛的高度相等.
观察图像可知,当甲蜡烛比乙蜡烛低.
方法指导
第(3)小问要抓住交点的意义,并结合图像求解.
例6
学校有一批复印任务,原来有甲复印社承接,按每100页40元计费.现在乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如图
根据图像回答下列问题:
(1)乙复印社的每月承包费是多少
(2)当每月复印多少页时,两复印社实际收费相同
(3)如果每月复印页数在1200页左右,那么学校应选择哪个复印社比较合算
分析
由图像可知,乙的图像与y轴的交点坐标为(0,200),说明乙每月的承包费为200元;而“收费相同”在图像上的反映就是两条直线的交点位置;对于选择哪家复印社比较合算,那就要看当x=1200时,哪条直线的位置“较低”了.
解
(1)乙复印社的每月承包费为200元;
(2)从图像上观察可知,当每月复印800页时,两复印社实际收费相同;
(3)如果每月复印页数在1200页左右,也就是当x=1200时,其在乙图像上的点低于甲图像上的点,故说明学校应选择乙复印社比较合算.
评析
根据条件,本题还可以依据图像写出收费y(元)与复印页数x(页)之间的函数关系式,甲为y=0.4x,乙为y=0.15x+200.这样就可以通过解方程以及计算来求出第(2),(3)问了.
【模拟试题】(答题时间:60分钟)
1.
若函数的图象经过点(1,2),则函数的表达式可能是
(写出一个即可)
2.
一次函数y=kx+b满足kb>0且y随x的增大而减小,则此函数图象不经过
(
)
A、第1象限
B、第2象限
C、第3象限
D、第4象限
3.
两个一次函数y1=mx+n,y2=nx+m,它们在同一坐标系中的图象可能是下图中的
(
)
4.
在函数y=-2x+3中,当自变量x满足
时,图象在第一象限.
5.
已知一次函数y=kx+b的图象经过点(0,1)且不经过第四象限,则满足以上条件的一个一次函数的解析式为
6.
某污水处理厂的一个净化池设有2个进水口和1个出水口,三个水口至少打开一个,每个进水口进水速度由图甲给出,出水口出水的速度由图乙给出.某一天0点到6点,该水池的蓄水量与时间的函数关系如图丙所示.通过对图象的观察,小亮得出了以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水;(3)4点到6点不进水也不出水.其中正确的是
(
)
A、(1)
B、(1)(2)
C、(1)(3)
D、(1)(2)(3)
7.
如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,能表示这个一次函数的解析式为
(
)
A.
2x-y+3=0
B.
x-y-3=0
C.
2y-x+3=0
D.
x+y-3=0
8.
如图,表示甲骑电动自行车和乙驾驶汽车均行驶90km的过程中,行驶的路程与经过的时间的函数关系,请根据图象填空:
出发早,早了
小时,
先到达,先到
小时,电动自行车的速度为
km/h,汽车的速度为
km/h.
9.
已知正比例函数y=k1x的图象与一次函数y=
k2x-9的图象相交于点P(3,-6).
(1)求k1、k2的值;
(2)如果一次函数y=
k1x-9的图象与x轴交于点A,求A的坐标.
10.
某出版社出版一种适合中学生阅读的科普读物,若该读物首次印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册)
5000
8000
10000
15000
……
成本y(元)
28500
36000
41000
53500
……
(1)经过对上表数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入48000元,那么能印读物多少册?
11.
某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,下图表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1、y2的解析式;
(2)解释图中表示的两种方案是如何付推销费的;
(3)如果你是推销员,应如何选择付费方案?
12.
电视台为某个广告公司特约播放甲、乙两部连续剧.经调查,播放甲连续剧平均每集有收视观众20万人次,播放乙连续剧平均每集有收视观众15万人次,公司要求电视台每周共播放7集.
(1)设一周内甲连续剧播x集,甲、乙两部连续剧观众的人次的总和为y万人次,求y关于x的函数关系式;
(2)已知电视台每周只能为该公司提供不超过300分钟的播放时间,并且播放甲连续剧每集需50分钟,播放乙连续剧每集需35分钟,请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集,才能使得每周收看甲、乙连续剧的观众的人次总和最大,并求出这个最大值.
【试题答案】
1.
y
=2x
2.
A
3.
B
4.
5.
y=x+1
6.
C
7.
D
8.
电动车,
2
,
汽车,
2
,
18
km/h,
60
km/h.
9.
(1)k1=-2,k2=1;
(2)(9,0)
10.
(1)
(2)12800
11.
(1)
(2)第一种情况是按照推销的件数提成;第二种情况是先付给推销员300元,然后再按推销的件数提成.
(3)当推销产品的件数等于30件时,两种方案一样,
然后再分大于30件和小于30件来考虑
12.
(1)y=5x+105
(2)略
【本讲教育信息】
一.
教学内容:
一次函数的图像、性质和应用;二元一次方程组的图像解法
[学习目标]
1.
理解一次函数的图像是一条直线以及它的性质,会画一次函数的图像.
2.
会应用一次函数的性质解决实际问题,能够用图像法解二元一次方程组.
3.
通过学习,进一步体会“数形结合”的数学思想方法以及数学建模的思想.
二.
重点、难点:
能够熟练地用描点法、两点法画出一次函数的图像,用图像法解二元一次方程组,理解一次函数性质并会应用一次函数解决问题是重点;难点是对一次函数性质的理解以及应用一次函数解决问题.
三.
知识要点:
1.
一次函数与正比例函数的图像
一般地,一次函数的图像是过(),(0,b)的一条直线;特殊的,正比例函数的图像是过(0,0),(1,k)的一条直线.
直线是由直线向上或向下平移单位得到的.或者说直线是由直线向右或向左平移单位得到的.
2.
一次函数的性质
(1)增减性:如果,那么y的值随x值的增大而增大;
如果,那么y的值随x值的增大而减小
(2)所通过的象限如下表
k,b的符号
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
图像
所通过的象限
一,二,三
一,三,四
一,二,四
二,三,四
3.
一次函数图像上任意一点的坐标与二元一次方程解的关系:
一次函数图像上任意一点的坐标都是二元一次方程的一个解;
以二元一次方程的解为坐标的点都在一次函数图像上.
4.
数形结合及数学建模思想方法的体会与应用也是本章的一个重要知识点.
【典型例题】
例1.
如图所示,两条直线分别表示函数和,请根据图像,回答下列问题:
(1)直线AB表示
的图像,直线OB表示
的图像.
(2)函数随x的增大而
,函数随x的减小而
.
分析
(1)观察图像可知,直线AB与直线OB的区别是直线OB经过原点,而正比例函数的图像是经过原点的一条直线,所以直线OB表示,直线AB表示.
(2)从左向右看两个图像的变化趋势可知,函数随x的增大而增大;函数随x的减小而增大
解
(1);
(2)增大;增大
方法指导
经过原点的直线是正比例函数的图像,不经过原点的直线是一般是一次函数的图像.
例2.
直线y=kx+b与直线y=kbx,它们在同一个坐标系中的图象大致为(
)
分
析
解决此题有效的方法是排除法.如我们以B为例,可以看出正比例函数kb>0,即k,b为同号;另外从一次函数y=kx+b的图像可以看出k<0,b>0,即k,b异号,所以出现矛盾情况.做此类题目的关键是对一次函数性质的理解和掌握.
解
A
例3
一次函数的图像过(3,0),且与坐标轴所围成的图形的面积为9,求一次函数的函数关系式.
分析
要求一次函数的函数关系式,必须知道函数图像经过两点的坐标,由条件知一个点的坐标,必须求出另一个点的坐标.由“图像与坐标轴所围成的面积为9”可求得另一个点的坐标.最后用待定系数法去求关系式.
解
如图,设一次函数的图像与x轴交于点A(3,0),与y轴交于点B(0,b),则OA=3,OB=.又,故B的坐标为(0,6)或(0,-6).
设一次函数的函数关系式为,则
得
所以一次函数的解析式为y=-2x+6或y=2x-6
评析
解决面积问题结合图形考虑,不但对问题容易把握,而且可以使问题解决的更全面.
例4
如图所表示甲、乙两名选手在一次自行车越野赛中,路程y(km)随时间x(min)变化的图像(全程).根据图像回答下列问题:
(1)求比赛开始多少分钟时,两人第一次相遇;
(2)求这次比赛的全程是多少千米;
(3)求比赛开始多少分钟时,两人第二次相遇.
分析
认真读图,通过图像上的一些特殊点,如图像与坐标轴的交点,图像的起、终点,图像上已用虚线表示出横、纵坐标的点等寻找突破口,如本题以A,B两点为突破口.
解
(1)当
把(15,5)和(33,7)代入得
当y=6时,有
∴比赛开始24min两人第一次相遇.
(2)设
∴
∴比赛的全程为12km.
(3)当
解得
解方程组
∴比赛开始38min两人第二次相遇.
评析
本题体现了从形到数的转化,是数形结合的具体运用,也是待定系数法的具体应用,此方法与方程、方程组的解法密不可分.
例5
在一次蜡烛燃烧实验中,甲、乙两根蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)的关系如图所示.请根据图象所提供的信息解答下列问题:
(1)甲、乙两根蜡烛燃烧前的高度分别是
,从点燃到燃尽所用的时间分别是
;
(2)分别求甲、乙两根蜡烛燃烧时y与x之间的函数关系式;
(3)当x为何值时,甲、乙两根蜡烛在燃烧过程中的高度相等?
分析
(1)纵轴表示蜡烛的高度.
(2)因为图像都是线段,所以它们的函数关系式都是一次函数.根据图像上提供的点的坐标用待定系数法分别求解.
(3)求出两条线段的交点坐标,结合图像的位置求解.
解
(1)30cm,
25cm;
2h,
2.5h
(2)设甲蜡烛燃烧时y与x函数关系式为
观察可知,它的图像经过点(2,0),
(0,30)
所以
解得
所以甲蜡烛燃烧时函数关系式为
设乙蜡烛燃烧时y与x函数关系式为
观察可知,它的图像经过点(2.5,0),
(0,25)
所以
解得
∴乙蜡烛燃烧时函数关系式为:
(3)当甲蜡烛与乙蜡烛的高度相等时,则
所以x=1时,甲蜡烛与乙蜡烛的高度相等.
观察图像可知,当甲蜡烛比乙蜡烛低.
方法指导
第(3)小问要抓住交点的意义,并结合图像求解.
例6
学校有一批复印任务,原来有甲复印社承接,按每100页40元计费.现在乙复印社表示:若学校先按月付给一定数额的承包费,则可按每100页15元收费.两复印社每月收费情况如图
根据图像回答下列问题:
(1)乙复印社的每月承包费是多少
(2)当每月复印多少页时,两复印社实际收费相同
(3)如果每月复印页数在1200页左右,那么学校应选择哪个复印社比较合算
分析
由图像可知,乙的图像与y轴的交点坐标为(0,200),说明乙每月的承包费为200元;而“收费相同”在图像上的反映就是两条直线的交点位置;对于选择哪家复印社比较合算,那就要看当x=1200时,哪条直线的位置“较低”了.
解
(1)乙复印社的每月承包费为200元;
(2)从图像上观察可知,当每月复印800页时,两复印社实际收费相同;
(3)如果每月复印页数在1200页左右,也就是当x=1200时,其在乙图像上的点低于甲图像上的点,故说明学校应选择乙复印社比较合算.
评析
根据条件,本题还可以依据图像写出收费y(元)与复印页数x(页)之间的函数关系式,甲为y=0.4x,乙为y=0.15x+200.这样就可以通过解方程以及计算来求出第(2),(3)问了.
【模拟试题】(答题时间:60分钟)
1.
若函数的图象经过点(1,2),则函数的表达式可能是
(写出一个即可)
2.
一次函数y=kx+b满足kb>0且y随x的增大而减小,则此函数图象不经过
(
)
A、第1象限
B、第2象限
C、第3象限
D、第4象限
3.
两个一次函数y1=mx+n,y2=nx+m,它们在同一坐标系中的图象可能是下图中的
(
)
4.
在函数y=-2x+3中,当自变量x满足
时,图象在第一象限.
5.
已知一次函数y=kx+b的图象经过点(0,1)且不经过第四象限,则满足以上条件的一个一次函数的解析式为
6.
某污水处理厂的一个净化池设有2个进水口和1个出水口,三个水口至少打开一个,每个进水口进水速度由图甲给出,出水口出水的速度由图乙给出.某一天0点到6点,该水池的蓄水量与时间的函数关系如图丙所示.通过对图象的观察,小亮得出了以下三个论断:(1)0点到3点只进水不出水;(2)3点到4点不进水只出水;(3)4点到6点不进水也不出水.其中正确的是
(
)
A、(1)
B、(1)(2)
C、(1)(3)
D、(1)(2)(3)
7.
如图,过点A的一次函数的图象与正比例函数y=2x的图象相交于点B,能表示这个一次函数的解析式为
(
)
A.
2x-y+3=0
B.
x-y-3=0
C.
2y-x+3=0
D.
x+y-3=0
8.
如图,表示甲骑电动自行车和乙驾驶汽车均行驶90km的过程中,行驶的路程与经过的时间的函数关系,请根据图象填空:
出发早,早了
小时,
先到达,先到
小时,电动自行车的速度为
km/h,汽车的速度为
km/h.
9.
已知正比例函数y=k1x的图象与一次函数y=
k2x-9的图象相交于点P(3,-6).
(1)求k1、k2的值;
(2)如果一次函数y=
k1x-9的图象与x轴交于点A,求A的坐标.
10.
某出版社出版一种适合中学生阅读的科普读物,若该读物首次印刷的印数不少于5000册时,投入的成本与印数间的相应数据如下:
印数x(册)
5000
8000
10000
15000
……
成本y(元)
28500
36000
41000
53500
……
(1)经过对上表数据的探究,发现这种读物的投入成本y(元)是印数x(册)的一次函数,求这个一次函数的解析式(不要求写出x的取值范围);
(2)如果出版社投入48000元,那么能印读物多少册?
11.
某公司推销一种产品,设x(件)是推销产品的数量,y(元)是推销费,下图表示了公司每月付给推销员推销费的两种方案,看图解答下列问题:
(1)求y1、y2的解析式;
(2)解释图中表示的两种方案是如何付推销费的;
(3)如果你是推销员,应如何选择付费方案?
12.
电视台为某个广告公司特约播放甲、乙两部连续剧.经调查,播放甲连续剧平均每集有收视观众20万人次,播放乙连续剧平均每集有收视观众15万人次,公司要求电视台每周共播放7集.
(1)设一周内甲连续剧播x集,甲、乙两部连续剧观众的人次的总和为y万人次,求y关于x的函数关系式;
(2)已知电视台每周只能为该公司提供不超过300分钟的播放时间,并且播放甲连续剧每集需50分钟,播放乙连续剧每集需35分钟,请你用所学知识求电视台每周应播放甲、乙两部连续剧各多少集,才能使得每周收看甲、乙连续剧的观众的人次总和最大,并求出这个最大值.
【试题答案】
1.
y
=2x
2.
A
3.
B
4.
5.
y=x+1
6.
C
7.
D
8.
电动车,
2
,
汽车,
2
,
18
km/h,
60
km/h.
9.
(1)k1=-2,k2=1;
(2)(9,0)
10.
(1)
(2)12800
11.
(1)
(2)第一种情况是按照推销的件数提成;第二种情况是先付给推销员300元,然后再按推销的件数提成.
(3)当推销产品的件数等于30件时,两种方案一样,
然后再分大于30件和小于30件来考虑
12.
(1)y=5x+105
(2)略
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
