江苏省徐州市2016-2017学年高二下期中考试理科数学试题 Word版含答案
文档属性
| 名称 | 江苏省徐州市2016-2017学年高二下期中考试理科数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 321.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-02 06:58:21 | ||
图片预览



文档简介
江苏省徐州市2016-2017学年高二下期中考试
理科数学试题
第Ⅰ卷(共70分)
一、填空题(每题5分,满分70分,将答案填在答题纸上)
1.复数
.
2.用反证法证明命题:“三角形的内角中至少有一个不大于”时,结论的否定是
..
3.从1到10的正整数中,任意抽取两个相加所得的和为奇数的不同情形的种数是
.(用数字作答).
4.由:①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形,写一个“三段论”形式的推理,则作为大前提、小前提和结论的依次为
.(写序号)
5.设:为纯虚数,且,则
.
6.观察下列各式:9-1=8,16-4=12,25-9=16,36-16=20,……,这些等式反映了自然数间的某种规律,设表示自然数,用关于的等式表示为
.
7.若,则的值为
.
8.现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是的正方形,其中一个的某顶点恰好是另一个的中心,则这两个正方形重叠部分的面积恒为.类比到空间,有两个棱长均为的正方体,若其中一个的某顶点恰好是另一个的中心,则这两个正方体重叠部分的体积恒为
.
9.用数学归纳法证明不等式成立,起始值应取为
.
10.用数学归纳法证明:,在第二步证明从到成立时,左边增加的项数是
(用含有的式子作答).
11.某班某天要安排语文、数学、政治、英语、体育、艺术6节课,要求数学课排在前3节,体育课不
排在第1节,则不同的排法种数为
.(用数字作答)
12.已知复数满足等式(是虚数单位).则的最小值是
.
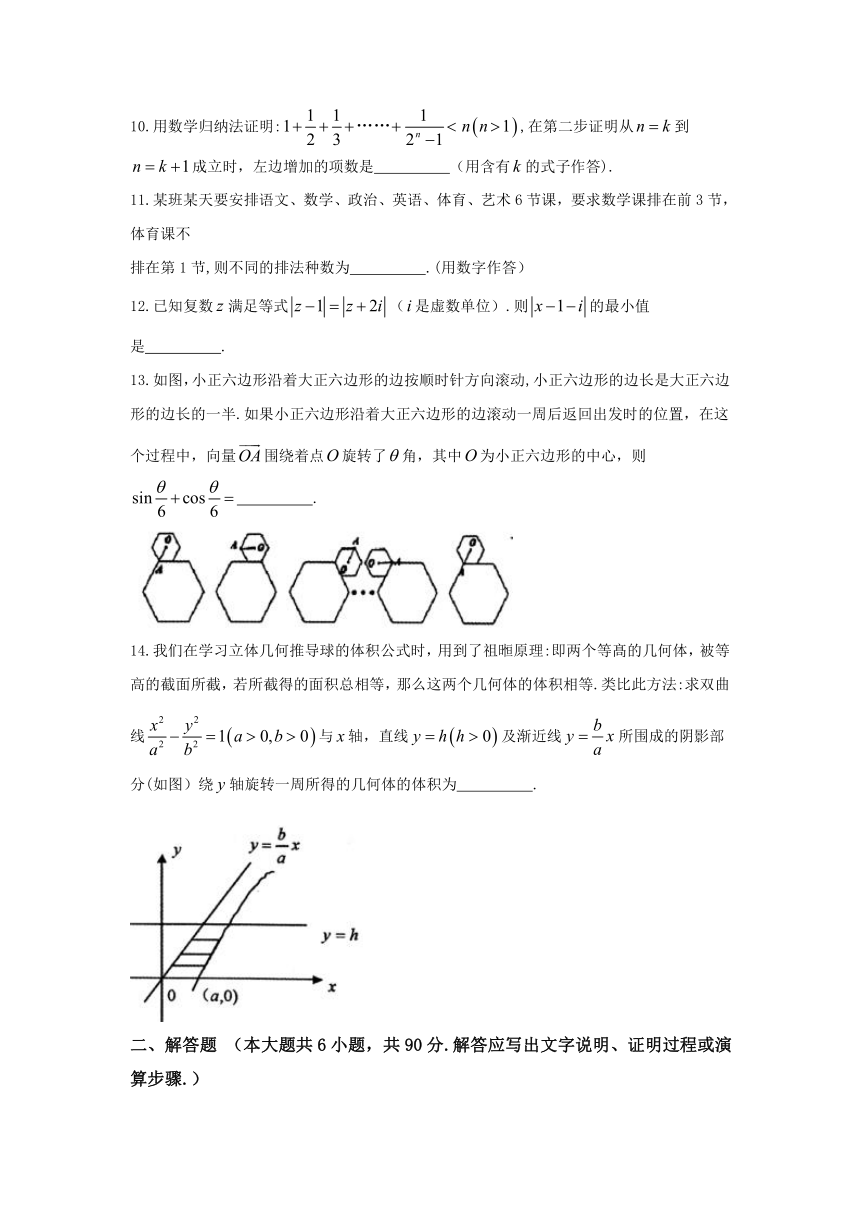
13.如图,小正六边形沿着大正六边形的边按顺时针方向滚动,小正六边形的边长是大正六边形的边长的一半.如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中,向量围绕着点旋转了角,其中为小正六边形的中心,则
.
14.我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等髙的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线与轴,直线及渐近线所围成的阴影部分(如图)绕轴旋转一周所得的几何体的体积为
.
二、解答题
(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)
15.设复数(,,是虚数单位),且复数满足,复数在复平面上对应的点在第一、三象限的角平分线上.
⑴求复数;
(2)若为纯虚数(其中),求实数的值.
16.阅读材料:根据两角和与差的正弦公式,有:,
,由得,令,,有,,代入得.
(1)利用上述结论,试求的值;
(2)类比上述推证方法,根据两角和与差的余弦公式,证明:.
17.已知的展开式中第3项的系数与第5项的系数之比为.
(1)求的值;
(2)求展开式中的常数项.
18.有男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
(3)既要有队长,又要有女运动员.
19.(1)找出一个等比数列,使得1,,4为其中的三项,并指出分别是的第几项;
(2)证明:
为无理数;
(3)证明:1,,4不可能为同一等差数列中的三项.
20.已知函数,,的图象恒过定点,且点既在的图象上,又在的导函数的图象上.
⑴求,的值;
(2)设,当且时,判断的符号,并说明理由;
(3)求证:
(且).
试卷答案
一、填空题
1..
2.三个角全大于.
3.25.
4..
5..
6..
7.1
8..
9.8.
10..
11.312
12..
13.-1.
14..
二、解答题
15.解⑴设,由得:.①
又复数在复平面上对应的点在第一、三象限的角平分线上,则即.②.
由①②联立方程组,解得,或,,
,∴,.
∴.
⑵由,可得
,
为纯虚数,∴,
解得.
16.解(1);
(2)因为,,
由得,
令,,有,,代入得.
17.解:⑴展开式的通项为,
∴展开式中第3项与第5项的系数分别为,,据题意得,
解得;
(2)∴展开式的通项为,
令得,
∴展开式中的常数项为.
18.解⑴第一步:选3名男运动员,有种选法.
第二步:选2名女运动员,有种选法.
共有(种)选法.
⑵“至少1名女运动员”的反面为“全是男运动员”.
从10人中任选5人,有种选法,其中全是男运动员的选法有种.
所以“至少有1名女运动员”的选法有(种).
(3)当有女队长时,其他人选法任意,共有种选法.不选女队长时,必选男队长,共有种选法.其中不含女运动员的选法有种,所以不选女队长时共有种选法.故既要有队长,又要有女运动员的选法有(种).
19.解(1)取首项为1,公比为,则,
则,,.
(2)证明:假设是有理数,则存在互质整数,,使得,
则,所以为偶数,设,为整数,则,所以也为偶数,
则,有公约数2,这与,互质相矛盾,
所以假设不成立,所以是有理数.
(3)证明:假设1,,4是同一等差数列中的三项,
且分别为第项且互不相等,
设公差为,显然,则,,
消去得,,
由都为整数,所以为有理数,
由(2)得是无理数,所以等式不可能成立,
所以假设不成立,即1,,4不可能为同一等差数列中的三项.
20.解⑴因为,所以恒过,所以,,所以,因为,,所以,即,;
(2)答:,即证且时,,异号;
因为,所以当时,,
因为,所以在单调递减,
又,所以,所以,
当时,,
因为,所以,所以,综上得证.
(3)由(2)知:当时,,
即,令,所以,
所以,,……,,
以上个式子相加,即得,
所以.
另法:(3)数学归纳法证明如下:
①时,左边,右边,左边-右边
∴左边>右边,所以,当时,不等式成立.
②假设当时,不等式成立,即成立.
那么,当时,左边,而右边,
要证:,即证:,
即证:,即证★,
由(2)知:当时,,且,所以,即,
∵∴∴★成立
所以,当时,不等式成立.
由①②知,(且)不等式成立.
理科数学试题
第Ⅰ卷(共70分)
一、填空题(每题5分,满分70分,将答案填在答题纸上)
1.复数
.
2.用反证法证明命题:“三角形的内角中至少有一个不大于”时,结论的否定是
..
3.从1到10的正整数中,任意抽取两个相加所得的和为奇数的不同情形的种数是
.(用数字作答).
4.由:①正方形的对角线相等;②矩形的对角线相等;③正方形是矩形,写一个“三段论”形式的推理,则作为大前提、小前提和结论的依次为
.(写序号)
5.设:为纯虚数,且,则
.
6.观察下列各式:9-1=8,16-4=12,25-9=16,36-16=20,……,这些等式反映了自然数间的某种规律,设表示自然数,用关于的等式表示为
.
7.若,则的值为
.
8.现有一个关于平面图形的命题:如图,同一个平面内有两个边长都是的正方形,其中一个的某顶点恰好是另一个的中心,则这两个正方形重叠部分的面积恒为.类比到空间,有两个棱长均为的正方体,若其中一个的某顶点恰好是另一个的中心,则这两个正方体重叠部分的体积恒为
.
9.用数学归纳法证明不等式成立,起始值应取为
.
10.用数学归纳法证明:,在第二步证明从到成立时,左边增加的项数是
(用含有的式子作答).
11.某班某天要安排语文、数学、政治、英语、体育、艺术6节课,要求数学课排在前3节,体育课不
排在第1节,则不同的排法种数为
.(用数字作答)
12.已知复数满足等式(是虚数单位).则的最小值是
.
13.如图,小正六边形沿着大正六边形的边按顺时针方向滚动,小正六边形的边长是大正六边形的边长的一半.如果小正六边形沿着大正六边形的边滚动一周后返回出发时的位置,在这个过程中,向量围绕着点旋转了角,其中为小正六边形的中心,则
.
14.我们在学习立体几何推导球的体积公式时,用到了祖暅原理:即两个等髙的几何体,被等高的截面所截,若所截得的面积总相等,那么这两个几何体的体积相等.类比此方法:求双曲线与轴,直线及渐近线所围成的阴影部分(如图)绕轴旋转一周所得的几何体的体积为
.
二、解答题
(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤.)
15.设复数(,,是虚数单位),且复数满足,复数在复平面上对应的点在第一、三象限的角平分线上.
⑴求复数;
(2)若为纯虚数(其中),求实数的值.
16.阅读材料:根据两角和与差的正弦公式,有:,
,由得,令,,有,,代入得.
(1)利用上述结论,试求的值;
(2)类比上述推证方法,根据两角和与差的余弦公式,证明:.
17.已知的展开式中第3项的系数与第5项的系数之比为.
(1)求的值;
(2)求展开式中的常数项.
18.有男运动员6名,女运动员4名,其中男女队长各1名.选派5人外出比赛,在下列情形中各有多少种选派方法?
(1)男运动员3名,女运动员2名;
(2)至少有1名女运动员;
(3)既要有队长,又要有女运动员.
19.(1)找出一个等比数列,使得1,,4为其中的三项,并指出分别是的第几项;
(2)证明:
为无理数;
(3)证明:1,,4不可能为同一等差数列中的三项.
20.已知函数,,的图象恒过定点,且点既在的图象上,又在的导函数的图象上.
⑴求,的值;
(2)设,当且时,判断的符号,并说明理由;
(3)求证:
(且).
试卷答案
一、填空题
1..
2.三个角全大于.
3.25.
4..
5..
6..
7.1
8..
9.8.
10..
11.312
12..
13.-1.
14..
二、解答题
15.解⑴设,由得:.①
又复数在复平面上对应的点在第一、三象限的角平分线上,则即.②.
由①②联立方程组,解得,或,,
,∴,.
∴.
⑵由,可得
,
为纯虚数,∴,
解得.
16.解(1);
(2)因为,,
由得,
令,,有,,代入得.
17.解:⑴展开式的通项为,
∴展开式中第3项与第5项的系数分别为,,据题意得,
解得;
(2)∴展开式的通项为,
令得,
∴展开式中的常数项为.
18.解⑴第一步:选3名男运动员,有种选法.
第二步:选2名女运动员,有种选法.
共有(种)选法.
⑵“至少1名女运动员”的反面为“全是男运动员”.
从10人中任选5人,有种选法,其中全是男运动员的选法有种.
所以“至少有1名女运动员”的选法有(种).
(3)当有女队长时,其他人选法任意,共有种选法.不选女队长时,必选男队长,共有种选法.其中不含女运动员的选法有种,所以不选女队长时共有种选法.故既要有队长,又要有女运动员的选法有(种).
19.解(1)取首项为1,公比为,则,
则,,.
(2)证明:假设是有理数,则存在互质整数,,使得,
则,所以为偶数,设,为整数,则,所以也为偶数,
则,有公约数2,这与,互质相矛盾,
所以假设不成立,所以是有理数.
(3)证明:假设1,,4是同一等差数列中的三项,
且分别为第项且互不相等,
设公差为,显然,则,,
消去得,,
由都为整数,所以为有理数,
由(2)得是无理数,所以等式不可能成立,
所以假设不成立,即1,,4不可能为同一等差数列中的三项.
20.解⑴因为,所以恒过,所以,,所以,因为,,所以,即,;
(2)答:,即证且时,,异号;
因为,所以当时,,
因为,所以在单调递减,
又,所以,所以,
当时,,
因为,所以,所以,综上得证.
(3)由(2)知:当时,,
即,令,所以,
所以,,……,,
以上个式子相加,即得,
所以.
另法:(3)数学归纳法证明如下:
①时,左边,右边,左边-右边
∴左边>右边,所以,当时,不等式成立.
②假设当时,不等式成立,即成立.
那么,当时,左边,而右边,
要证:,即证:,
即证:,即证★,
由(2)知:当时,,且,所以,即,
∵∴∴★成立
所以,当时,不等式成立.
由①②知,(且)不等式成立.
同课章节目录
