陕西省黄陵中学高新部2016-2017学年高一下学期期中考试数学试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学高新部2016-2017学年高一下学期期中考试数学试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 211.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-04 21:28:21 | ||
图片预览



文档简介
黄陵中学高新部2016-2017学年度第二学期期中考试
高一数学试题
(时间120分钟,满分150分)
一、选择题(共12小题,每小题5分,共60分)
1.已知直线l∥平面α,P∈α,那么过点P且平行于l的直线( )
A.只有一条,不在平面α内
B.只有一条,在平面α内
C.有两条,不一定都在平面α内
D.有无数条,不一定都在平面α内
2.三棱锥S ABC中,E,F分别是SB,SC上的点,且EF∥平面ABC,则( )
A.EF与BC相交
B.EF与BC平行
C.EF与BC异面
D.以上均有可能
3.直线a∥平面α,α内有n条直线交于一点,那么这n条直线中与直线a平行的( )
A.至少有一条
B.至多有一条
C.有且只有一条
D.没有
4.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线l:x-y-1=0对称,则圆C2的方程为( )
A.(x-2)2+(y+2)2=1
B.(x+2)2+(y-2)2=1
C.(x-2)2+(y-2)2=1
D.(x-2)2+(y-1)2=1
5.面积为Q的正方形,绕其一边旋转一周,则所得几何体的侧面积为( )
A.πQ
B.2πQ
C.3πQ
D.4πQ
6.关于直线m,n与平面α,β,有下列四个命题:
①m∥α,n∥β且α∥β,则m∥n;
②m⊥α,n⊥β
且α⊥β,则m⊥n;
③m⊥α,n∥β
且α∥β,则m⊥n;
④m∥α,n⊥β且α⊥β,则m∥n.
其中真命题的序号是( )
A.①②
B.③④
C.①④
D.②③
7.平面直角坐标系中,直线x+y+2=0的斜率为( )
A.
B.-
C.
D.-
8.直线ax+by=1(a,b均不为0)与两坐标轴围成的三角形的面积为( )
A.ab
B.|ab|
C.
D.
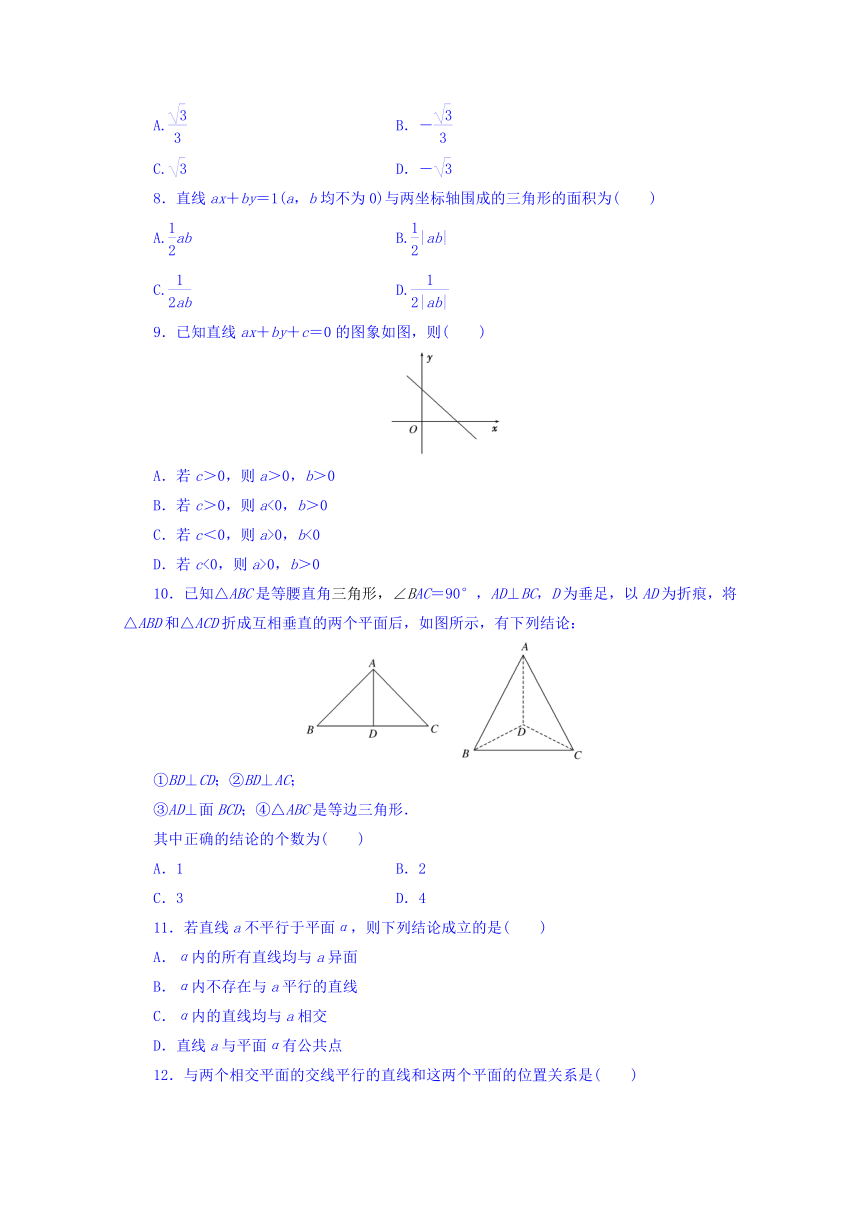
9.已知直线ax+by+c=0的图象如图,则( )
A.若c>0,则a>0,b>0
B.若c>0,则a<0,b>0
C.若c<0,则a>0,b<0
D.若c<0,则a>0,b>0
10.已知△ABC是等腰直角三角形,∠BAC=90°,AD⊥BC,D为垂足,以AD为折痕,将△ABD和△ACD折成互相垂直的两个平面后,如图所示,有下列结论:
①BD⊥CD;②BD⊥AC;
③AD⊥面BCD;④△ABC是等边三角形.
其中正确的结论的个数为( )
A.1
B.2
C.3
D.4
11.若直线a不平行于平面α,则下列结论成立的是( )
A.α内的所有直线均与a异面
B.α内不存在与a平行的直线
C.α内的直线均与a相交
D.直线a与平面α有公共点
12.与两个相交平面的交线平行的直线和这两个平面的位置关系是( )
A.都平行
B.都相交
C.在两平面内
D.至少和其中一个平行
二、填空题(共4小题,每小题5分,共20分)
13.A,B是直线l外两点,过A,B且与l平行的平面有________个.
14.圆x2+y2-4x-2y-11=0上的点到直线x+y-13=0的最大距离与最小距离之差是________.
15.在三棱柱ABC A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是________.
16.在长方体ABCD A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有________个.
三、解答题(共6小题,共70分,解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)求与点P(4,3)的距离为5,且在两坐标轴的截距相等的直线方程.
18.(本小题满分12分)已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0,直线l1:x-3y-3=0.
(1)求证:不论m取何值,圆心必在直线l1上;
(2)与l1平行的直线中,哪些与圆相交、相切、相离.
19.(本小题满分12分)设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
20.(本小题满分12分)如图,在底面为平行四边形的四棱锥P ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.求证:
(1)AC⊥PB;
(2)PB∥平面AEC.
21.(本小题满分12分)如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC=CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD.
(1)求证:平面PAD⊥平面PCD;
(2)若E是PC的中点,求三棱锥A PEB的体积.
22.(本小题满分12分)已知三角形的顶点坐标是A(-5,0),B(3,-3),C(0,2),试求这个三角形的三条边所在直线的方程.
参考答案及解析
1.解析:如图所示,
因为l∥平面α,P∈α,
所以直线l与点P确定一个平面β,
α∩β=m,
所以P∈m,所以l∥m且m是唯一的.
答案:B
2.解析:由线面平行的性质定理可知EF∥BC.
答案:
B
3.解析:直线a和该交点确定一个平面,由线面平行的性质得,此平面与平面α的交线与a平行,故至多有一条.
答案:4.解析:选A 可知C1(-1,
1),直线l的斜率为1,设圆C2的圆心坐标为(a,b),则kC1C2=,线段C1C2的中点为.∵圆C2与圆C1关于直线l对称,∴线段C1C2被直线l垂直平分,∴有解得
∴圆C2的方程为(x-2)2+(y+2)2=1,故选A.
解析:选B 设正方形边长为a,则a=,S侧=2π·a·a=2πQ
6.解析:选D 对于①,m与n可能平行,可能相交,也可能异面,所以①是假命题;②是真命题;对于③,m⊥α,α∥β m⊥β,若n∥β,必有m⊥n,所以③是真命题,从而④是假命题,故选D.
7.答案:B
8.答案:D
9.答案:D
10.解析:选D ∵AD⊥BD,AD⊥CD,∴∠BDC是二面角B AD C的平面角.又平面ABD⊥平面ACD,∴∠BDC=90°,∴BD⊥CD,同时,AD⊥平面BCD,
BD⊥平面ACD,∴BD⊥AC,∵DA=DB=DC,
∴Rt△ABD、Rt△BCD、Rt△ACD全等,
∴△ABC是等边三角形,故①②③④均正确.
11.解析:若直线a不平行平面α,则a∩α=A或a α,故D项正确.
答案:D
12.解析:若该直线不属于任何一个平面,则其与两平面平行;若该直线属于其中一个平面,则其必和另一个平面平行.
答案:D
13.解析:当直线AB与l相交时,有0个;当直线AB与l异面时,有1个;当直线AB∥l时,有无数个.
答案:0,1或无数个
14.解析:圆的标准方程为(x-2)2+(y-1)2=16,圆心到直线的距离为d==5,所以,圆上的点到直线的最大距离为5+4,圆上的点到直线的最小距离为5-4,所以,
最大距离与最小距离之差是8.
答案:8
15.解析:过A作AE⊥BC于点E,则易知AE⊥面BB1C1C,则∠ADE即为所求,又tan∠ADE==,故∠ADE=60°.
答案:60°
16.解析:如图所示,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.
答案:3
17.解:设所求直线方程为y=kx或+=1(a≠0).
对于y=kx,5=,9k2+24k+16=0,
解之得k=-.
对于x+y=a,5=,
解之得a=7+5或7-5.
故所求直线方程为y=-x或x+y-7-5=0或x+y-7+5=0.
18.解:(1)证明:将圆的方程化为标准方程为
(x-3m)2+2=25,
∴圆心是(3m,m-1).
∵3m-3(m-1)-3=0,
∴不论m取何值,圆心必在直线l1上.
(2)设与直线l1平行的直线l2的方程为x-3y+b=0(b≠-3),
则圆心到直线l2的距离为d==.
∵圆的半径r=5,
∴当d<r,即<5,
亦即-5-3当d=r,即=5,b=-5-3或b=5-3时,直线与圆相切;
当d>r,即>5,b<-5-3或b>5-3时,直线与圆相离.
19.解:(1)当a=-1时,直线l的方程为y+3=0,不符合题意;
当a≠-1时,直线l在x轴上的截距为,在y轴上的截距为a-2,因为l在两坐标轴上的截距相等,
所以=a-2,解得a=2或a=0,
所以直线l的方程为3x+y=0或x+y+2=0.
(2)将直线l的方程化为y=-(a+1)x+a-2,所以或
解得a≤-1.
综上所述,实数a的取值范围是{a|a≤-1}.
20.解:(1)由PA⊥平面ABCD可得PA⊥AC,又AB⊥AC,所以AC⊥平面PAB,
所以AC⊥PB.
(2)连接BD交AC于点O,连接EO,则EO是△PDB的中位线,
所以EO∥PB.
又因为PB 面AEC,EO 面AEC,所以PB∥平面AEC.
21.解:(1)
证明:∵PD⊥底面ABCD,
∴PD⊥AD.
又由于CP∥AB,CP⊥CB,AB=BC,
∴ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,故AD⊥平面PCD,
∵AD 平面PAD,
∴平面PAD⊥平面PCD.
(2)∵AD∥BC,又BC 平面PBC,AD 平面PBC,
∴AD∥平面PBC,
∴点A到平面PBC的距离即为点D到平面PBC的距离.
又∵PD=DC,E是PC的中点,
∴DE⊥PC.
由(1)知有AD⊥平面PCD,∴AD⊥DE.
由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,可得DE⊥平面PBC.
∴DE=,PC=2,
又∵AD⊥平面PCD,
∴AD⊥CP,
∵AD∥BC,∴CP⊥BC,
∴S△PEB=S△PBC=×=,
∴VA PEB=VD PEB=×DE×S△PEB=.
22.解:直线AB的斜率kAB==-,过点A(-5,0),由点斜式得直线AB的方程为y=-(x+5),即3x+8y+15=0;同理,kBC==-,kAC==,直线BC,AC的方程分别为5x+3y-6=0,2x-5y+10=0.
高一数学试题
(时间120分钟,满分150分)
一、选择题(共12小题,每小题5分,共60分)
1.已知直线l∥平面α,P∈α,那么过点P且平行于l的直线( )
A.只有一条,不在平面α内
B.只有一条,在平面α内
C.有两条,不一定都在平面α内
D.有无数条,不一定都在平面α内
2.三棱锥S ABC中,E,F分别是SB,SC上的点,且EF∥平面ABC,则( )
A.EF与BC相交
B.EF与BC平行
C.EF与BC异面
D.以上均有可能
3.直线a∥平面α,α内有n条直线交于一点,那么这n条直线中与直线a平行的( )
A.至少有一条
B.至多有一条
C.有且只有一条
D.没有
4.已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线l:x-y-1=0对称,则圆C2的方程为( )
A.(x-2)2+(y+2)2=1
B.(x+2)2+(y-2)2=1
C.(x-2)2+(y-2)2=1
D.(x-2)2+(y-1)2=1
5.面积为Q的正方形,绕其一边旋转一周,则所得几何体的侧面积为( )
A.πQ
B.2πQ
C.3πQ
D.4πQ
6.关于直线m,n与平面α,β,有下列四个命题:
①m∥α,n∥β且α∥β,则m∥n;
②m⊥α,n⊥β
且α⊥β,则m⊥n;
③m⊥α,n∥β
且α∥β,则m⊥n;
④m∥α,n⊥β且α⊥β,则m∥n.
其中真命题的序号是( )
A.①②
B.③④
C.①④
D.②③
7.平面直角坐标系中,直线x+y+2=0的斜率为( )
A.
B.-
C.
D.-
8.直线ax+by=1(a,b均不为0)与两坐标轴围成的三角形的面积为( )
A.ab
B.|ab|
C.
D.
9.已知直线ax+by+c=0的图象如图,则( )
A.若c>0,则a>0,b>0
B.若c>0,则a<0,b>0
C.若c<0,则a>0,b<0
D.若c<0,则a>0,b>0
10.已知△ABC是等腰直角三角形,∠BAC=90°,AD⊥BC,D为垂足,以AD为折痕,将△ABD和△ACD折成互相垂直的两个平面后,如图所示,有下列结论:
①BD⊥CD;②BD⊥AC;
③AD⊥面BCD;④△ABC是等边三角形.
其中正确的结论的个数为( )
A.1
B.2
C.3
D.4
11.若直线a不平行于平面α,则下列结论成立的是( )
A.α内的所有直线均与a异面
B.α内不存在与a平行的直线
C.α内的直线均与a相交
D.直线a与平面α有公共点
12.与两个相交平面的交线平行的直线和这两个平面的位置关系是( )
A.都平行
B.都相交
C.在两平面内
D.至少和其中一个平行
二、填空题(共4小题,每小题5分,共20分)
13.A,B是直线l外两点,过A,B且与l平行的平面有________个.
14.圆x2+y2-4x-2y-11=0上的点到直线x+y-13=0的最大距离与最小距离之差是________.
15.在三棱柱ABC A1B1C1中,各棱长相等,侧棱垂直于底面,点D是侧面BB1C1C的中心,则AD与平面BB1C1C所成角的大小是________.
16.在长方体ABCD A1B1C1D1的六个表面与六个对角面(面AA1C1C、面ABC1D、面ADC1B1、面BB1D1D、面A1BCD1及面A1B1CD)所在的平面中,与棱AA1平行的平面共有________个.
三、解答题(共6小题,共70分,解答时应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)求与点P(4,3)的距离为5,且在两坐标轴的截距相等的直线方程.
18.(本小题满分12分)已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0,直线l1:x-3y-3=0.
(1)求证:不论m取何值,圆心必在直线l1上;
(2)与l1平行的直线中,哪些与圆相交、相切、相离.
19.(本小题满分12分)设直线l的方程为(a+1)x+y+2-a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
20.(本小题满分12分)如图,在底面为平行四边形的四棱锥P ABCD中,AB⊥AC,PA⊥平面ABCD,且PA=AB,点E是PD的中点.求证:
(1)AC⊥PB;
(2)PB∥平面AEC.
21.(本小题满分12分)如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC=CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD.
(1)求证:平面PAD⊥平面PCD;
(2)若E是PC的中点,求三棱锥A PEB的体积.
22.(本小题满分12分)已知三角形的顶点坐标是A(-5,0),B(3,-3),C(0,2),试求这个三角形的三条边所在直线的方程.
参考答案及解析
1.解析:如图所示,
因为l∥平面α,P∈α,
所以直线l与点P确定一个平面β,
α∩β=m,
所以P∈m,所以l∥m且m是唯一的.
答案:B
2.解析:由线面平行的性质定理可知EF∥BC.
答案:
B
3.解析:直线a和该交点确定一个平面,由线面平行的性质得,此平面与平面α的交线与a平行,故至多有一条.
答案:4.解析:选A 可知C1(-1,
1),直线l的斜率为1,设圆C2的圆心坐标为(a,b),则kC1C2=,线段C1C2的中点为.∵圆C2与圆C1关于直线l对称,∴线段C1C2被直线l垂直平分,∴有解得
∴圆C2的方程为(x-2)2+(y+2)2=1,故选A.
解析:选B 设正方形边长为a,则a=,S侧=2π·a·a=2πQ
6.解析:选D 对于①,m与n可能平行,可能相交,也可能异面,所以①是假命题;②是真命题;对于③,m⊥α,α∥β m⊥β,若n∥β,必有m⊥n,所以③是真命题,从而④是假命题,故选D.
7.答案:B
8.答案:D
9.答案:D
10.解析:选D ∵AD⊥BD,AD⊥CD,∴∠BDC是二面角B AD C的平面角.又平面ABD⊥平面ACD,∴∠BDC=90°,∴BD⊥CD,同时,AD⊥平面BCD,
BD⊥平面ACD,∴BD⊥AC,∵DA=DB=DC,
∴Rt△ABD、Rt△BCD、Rt△ACD全等,
∴△ABC是等边三角形,故①②③④均正确.
11.解析:若直线a不平行平面α,则a∩α=A或a α,故D项正确.
答案:D
12.解析:若该直线不属于任何一个平面,则其与两平面平行;若该直线属于其中一个平面,则其必和另一个平面平行.
答案:D
13.解析:当直线AB与l相交时,有0个;当直线AB与l异面时,有1个;当直线AB∥l时,有无数个.
答案:0,1或无数个
14.解析:圆的标准方程为(x-2)2+(y-1)2=16,圆心到直线的距离为d==5,所以,圆上的点到直线的最大距离为5+4,圆上的点到直线的最小距离为5-4,所以,
最大距离与最小距离之差是8.
答案:8
15.解析:过A作AE⊥BC于点E,则易知AE⊥面BB1C1C,则∠ADE即为所求,又tan∠ADE==,故∠ADE=60°.
答案:60°
16.解析:如图所示,结合图形可知AA1∥平面BB1C1C,AA1∥平面DD1C1C,AA1∥平面BB1D1D.
答案:3
17.解:设所求直线方程为y=kx或+=1(a≠0).
对于y=kx,5=,9k2+24k+16=0,
解之得k=-.
对于x+y=a,5=,
解之得a=7+5或7-5.
故所求直线方程为y=-x或x+y-7-5=0或x+y-7+5=0.
18.解:(1)证明:将圆的方程化为标准方程为
(x-3m)2+2=25,
∴圆心是(3m,m-1).
∵3m-3(m-1)-3=0,
∴不论m取何值,圆心必在直线l1上.
(2)设与直线l1平行的直线l2的方程为x-3y+b=0(b≠-3),
则圆心到直线l2的距离为d==.
∵圆的半径r=5,
∴当d<r,即<5,
亦即-5-3
当d>r,即>5,b<-5-3或b>5-3时,直线与圆相离.
19.解:(1)当a=-1时,直线l的方程为y+3=0,不符合题意;
当a≠-1时,直线l在x轴上的截距为,在y轴上的截距为a-2,因为l在两坐标轴上的截距相等,
所以=a-2,解得a=2或a=0,
所以直线l的方程为3x+y=0或x+y+2=0.
(2)将直线l的方程化为y=-(a+1)x+a-2,所以或
解得a≤-1.
综上所述,实数a的取值范围是{a|a≤-1}.
20.解:(1)由PA⊥平面ABCD可得PA⊥AC,又AB⊥AC,所以AC⊥平面PAB,
所以AC⊥PB.
(2)连接BD交AC于点O,连接EO,则EO是△PDB的中位线,
所以EO∥PB.
又因为PB 面AEC,EO 面AEC,所以PB∥平面AEC.
21.解:(1)
证明:∵PD⊥底面ABCD,
∴PD⊥AD.
又由于CP∥AB,CP⊥CB,AB=BC,
∴ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,故AD⊥平面PCD,
∵AD 平面PAD,
∴平面PAD⊥平面PCD.
(2)∵AD∥BC,又BC 平面PBC,AD 平面PBC,
∴AD∥平面PBC,
∴点A到平面PBC的距离即为点D到平面PBC的距离.
又∵PD=DC,E是PC的中点,
∴DE⊥PC.
由(1)知有AD⊥平面PCD,∴AD⊥DE.
由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,可得DE⊥平面PBC.
∴DE=,PC=2,
又∵AD⊥平面PCD,
∴AD⊥CP,
∵AD∥BC,∴CP⊥BC,
∴S△PEB=S△PBC=×=,
∴VA PEB=VD PEB=×DE×S△PEB=.
22.解:直线AB的斜率kAB==-,过点A(-5,0),由点斜式得直线AB的方程为y=-(x+5),即3x+8y+15=0;同理,kBC==-,kAC==,直线BC,AC的方程分别为5x+3y-6=0,2x-5y+10=0.
同课章节目录
