湖南省双峰县一中2016-2017学年高一下学期期中考试数学(文)试卷
文档属性
| 名称 | 湖南省双峰县一中2016-2017学年高一下学期期中考试数学(文)试卷 |
|
|
| 格式 | zip | ||
| 文件大小 | 341.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-05 16:26:41 | ||
图片预览




文档简介
双峰一中2017年上学期高一期中考试试题数学(文科)
一.选择题:
1.把38化为二进制数为(
)
A.
B.
C.
D.
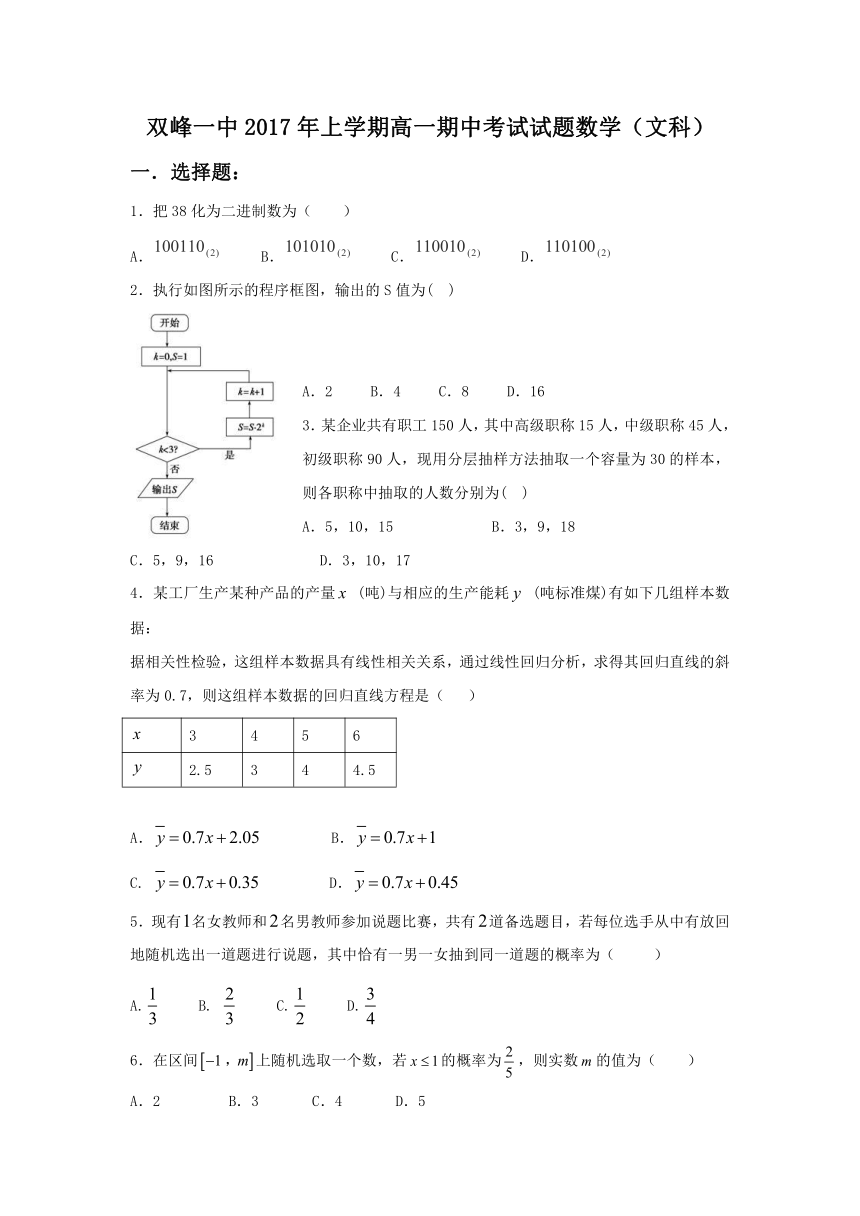
2.执行如图所示的程序框图,输出的S值为(
)
A.2
B.4
C.8
D.16
3.某企业共有职工150人,其中高级职称
( http: / / www.21cnjy.com )15人,中级职称45人,初级职称90人,现用分层抽样方法抽取一个容量为30的样本,则各职称中抽取的人数分别为(
)
A.5,10,15
B.3,9,18
C.5,9,16
D.3,10,17
4.某工厂生产某种产品的产量
(吨)与相应的生产能耗
(吨标准煤)有如下几组样本数据:
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是(
)
3
4
5
6
2.5
3
4
4.5
A.
B.
C.
D.
5.现有名女教师和名男教师参加说题比赛,共有道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为(
)
A.
B.
C.
D.
6.在区间上随机选取一个数,若的概率为,则实数的值为(
)
A.2
B.3
C.4
D.5
7.某扇形的半径为,它的弧长为,那么该扇形圆心角为
A.2°
B.2
C.4°
D.4
8.已知,则的值为(
)
A、
B、
C、
D、
9.已知tan,是关于x的方程x2-kx+k2-3=0的两个实根,且3π<<,则cos+sin=
(
)
A.
B.
C.
-
D.
-
10.要得到函数的图象,只需要将函数的图象(
)
A.向左平移个单位
B.向右平移个单位
C.向左平移个单位
D.向右平移个单位
11.函数的部分图象如图所示,则函数的解析式为(
)
( http: / / www.21cnjy.com )
A.
B.
C.
D.
12.已知函数,若与()图象的公共点中,相邻两个公共点的距离的最大值为,则的值为(
)
A.
B.1
C.
D.2
二.填空题:
13.为了了解某校高三男生的身体状况,抽查
( http: / / www.21cnjy.com )了部分男生的体重,将所得数据整理后,画出了频率分布直方图(如下图).已知图中从左到右的前3个小组的频率之比为1﹕2﹕3,第2小组的频数为12,则被抽查的男生的人数是
.
( http: / / www.21cnjy.com )
14.已知样本数据的方差,则样本数据的方差为
.
15.已知函数与函数的部分图像如右图所示,则____________.
( http: / / www.21cnjy.com )
16.给出如下五个结论:
①y=sinx在第一象限内是增函数;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cosx+sin(-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+|的最小正周期为π.
其中正确结论的序号是 .
三.解答题:
17.(10分)某校从高二年级学生中随机抽
( http: / / www.21cnjy.com )取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
18.一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
投入促销费用x(万元)
2
3
5
6
商场实际营销额y(万元)
100
200
300
400
(1)求出x,y之间的回归直线方程=x+;
(2)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
(注:
)
19.投掷一个质地均匀的、
( http: / / www.21cnjy.com )每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
20.已知.
(1)若,求的值;
(2)若为第二象限角,且,求的值.
21.已知函数()的最小正周期为.
(1)求函数的单调增区间;
(2)将函数的图像向左平移个单位,再向上平移个单位,得到函数的图像.求在区间上零点的个数.
22.如图为函数的部分图象.
(1)求函数解析式;
(2)若方程在上有两个不相等的实数根,则实数的取值范围.
数学(文科)
参考答案
一:选择题
1.A
2.C
3.B
4.C
5.C
6.C
7.B
8.A
9.C
10.B
11.B
12.C
二:填空题
13.48
14.12
15.
16.④
三:解答题
17.(1)860(2)75,75,74.2
【解析】
试题分析:(1)根据频率分布直方图可求
( http: / / www.21cnjy.com )得成绩不低于60分的概率值,结合样本容量可求得相应的人数;(2)众数为出现的次数最多的数,中位数为由小到大排列后的位于中间的数,平均数为各组的频率与该组的频数成绩之和
试题解析:(1)成绩不低于60分所占的频率为:1-(0.004+0.010)
10=0.86
所以成绩不低于60分的人数估计值为:1000
0.86=860(人)
-----------5分
(2)众数估计值:75
------------6分
设中位数为x,则(x-70)
0.032=0.5-0.04-0.1-0.2,解得x=75
---------8分
平均数估计值:s----10分
考点:频率分布直方图
18.
(1)因为x==4,y==250,
则=4+1+1+4=10,
(xi-x)(yi-y)=(-2)×(-150)+(-1)×(-50)+1×50+2×150=700,
所以=
( http: / / www.21cnjy.com )==70,
=y-x=250-70×4=-30.
故所求的回归直线方程为=70x-30.
(2)由题意得70x-30≥600,即x≥=9,所以若该商场计划营销额不低于600万元,则至少要投入9万元的促销费用.
19.(1)
(2)
【解析】
试题分析:(1)本小题是古典概型问
( http: / / www.21cnjy.com )题,欲求出点P落在区域C:x2+y2≤10内的概率,只须求出满足:x2+y2≤10上的点P的坐标有多少个,再将求得的值与整个点P的坐标个数求比值即得.(2)本小题是几何概型问题,欲求豆子落在区域M上的概率,只须求出满足:“豆子落在区域M上的概率”的区域的面积,再将求得的面积值与整个区域C的面积求比值即得试题解析:(1)以0、2、4为横、纵坐标的点P有(0,0)、(0,2)、(0,4)、(2,0)、(2,2)、(2,4)、(4,0)、(4,2)、(4,4)共9个,而这些点中,落在区域C内的点有:(0,0)、(0,2)、(2,0)、(2,2)共4个,∴所求概率为P=.
(2)∵区域M的面积为4,而区域C的面积为10π,
∴所求概率为P==.
( http: / / www.21cnjy.com )
考点:古典概型概率与几何概型概率
20.(1);(2).
【解析】
试题分析:(1)根据三角恒等变换的公式,化简,即可求解当时,的值;(2)由,解得,进而求解的值.
试题解析:
.
(1).
(2),∴,
∵是第二象限角,∴,
∴.
考点:三角函数的化简求值.
21.(1)函数的单调增区间;(2)在上有个零点.
【解析】
试题分析:(1)先由三角函数的周期计算公式得到,从而可确定,将当成一个整体,由正弦函数的性质得到,解出的范围,写成区间即是所求函数的单调递增区间;(2)将函数的图像向左平移个单位,再向上平移1个单位,得到的图像,即,由正弦函数的图像与性质得到该函数在一个周期内函数零点的个数,而恰为个周期,从而可得在上零点的个数.
试题解析:(1)由周期为,得,得
由正弦函数的单调增区间得
,得
所以函数的单调增区间
(2)将函数的图像向左平移个单位,再向上平移1个单位
得到的图像,所以
令,得或
所以函数在每个周期上恰有两个零点,恰为个周期,故在上有个零点.
考点:1.三角函数的图像与性质;2.函数的零点.
22.(1);(2).
【解析】【试题分析】(1)依据题设借助函数的图像探求函数解析式中的参数;(2)画出函数的图像借助图形的直观探求参数的范围。
(1)由题中的图象知,
,
,即,所以,
根据五点作图法,令,得到,
因为,所以,
.
(2)由在上的图象知,当上有两个不同的实根.
点睛:本题以函数的图像为背景,设置了三道与正弦函数图像有关的问题,旨在考查形如的三角函数的图像与性质。求解第一问时,依据题设借助函数的图像中的数据信息探求出函数解析式中的参数;解答第二问时,画出函数的图像借助图形的直观探求参数使得问题获解。
一.选择题:
1.把38化为二进制数为(
)
A.
B.
C.
D.
2.执行如图所示的程序框图,输出的S值为(
)
A.2
B.4
C.8
D.16
3.某企业共有职工150人,其中高级职称
( http: / / www.21cnjy.com )15人,中级职称45人,初级职称90人,现用分层抽样方法抽取一个容量为30的样本,则各职称中抽取的人数分别为(
)
A.5,10,15
B.3,9,18
C.5,9,16
D.3,10,17
4.某工厂生产某种产品的产量
(吨)与相应的生产能耗
(吨标准煤)有如下几组样本数据:
据相关性检验,这组样本数据具有线性相关关系,通过线性回归分析,求得其回归直线的斜率为0.7,则这组样本数据的回归直线方程是(
)
3
4
5
6
2.5
3
4
4.5
A.
B.
C.
D.
5.现有名女教师和名男教师参加说题比赛,共有道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为(
)
A.
B.
C.
D.
6.在区间上随机选取一个数,若的概率为,则实数的值为(
)
A.2
B.3
C.4
D.5
7.某扇形的半径为,它的弧长为,那么该扇形圆心角为
A.2°
B.2
C.4°
D.4
8.已知,则的值为(
)
A、
B、
C、
D、
9.已知tan,是关于x的方程x2-kx+k2-3=0的两个实根,且3π<<,则cos+sin=
(
)
A.
B.
C.
-
D.
-
10.要得到函数的图象,只需要将函数的图象(
)
A.向左平移个单位
B.向右平移个单位
C.向左平移个单位
D.向右平移个单位
11.函数的部分图象如图所示,则函数的解析式为(
)
( http: / / www.21cnjy.com )
A.
B.
C.
D.
12.已知函数,若与()图象的公共点中,相邻两个公共点的距离的最大值为,则的值为(
)
A.
B.1
C.
D.2
二.填空题:
13.为了了解某校高三男生的身体状况,抽查
( http: / / www.21cnjy.com )了部分男生的体重,将所得数据整理后,画出了频率分布直方图(如下图).已知图中从左到右的前3个小组的频率之比为1﹕2﹕3,第2小组的频数为12,则被抽查的男生的人数是
.
( http: / / www.21cnjy.com )
14.已知样本数据的方差,则样本数据的方差为
.
15.已知函数与函数的部分图像如右图所示,则____________.
( http: / / www.21cnjy.com )
16.给出如下五个结论:
①y=sinx在第一象限内是增函数;
②存在区间(a,b),使y=cosx为减函数而sinx<0;
③y=tanx在其定义域内为增函数;
④y=cosx+sin(-x)既有最大值和最小值,又是偶函数;
⑤y=sin|2x+|的最小正周期为π.
其中正确结论的序号是 .
三.解答题:
17.(10分)某校从高二年级学生中随机抽
( http: / / www.21cnjy.com )取50名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100],得到如图所示的频率分布直方图.
(1)若该校高二年级共有学生1000人,试估计成绩不低于60分的人数;
(2)求该校高二年级全体学生期中考试成绩的众数、中位数和平均数的估计值.
18.一家商场为了确定营销策略,进行了投入促销费用x和商场实际销售额y的试验,得到如下四组数据.
投入促销费用x(万元)
2
3
5
6
商场实际营销额y(万元)
100
200
300
400
(1)求出x,y之间的回归直线方程=x+;
(2)若该商场计划营销额不低于600万元,则至少要投入多少万元的促销费用?
(注:
)
19.投掷一个质地均匀的、
( http: / / www.21cnjy.com )每个面上标有一个数字的正方体玩具,它的六个面中,有两个面标的数字是0,两个面标的数字是2,两个面标的数字是4,将此玩具连续抛掷两次,以两次朝上一面的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域C:x2+y2≤10内的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒豆子,求豆子落在区域M上的概率.
20.已知.
(1)若,求的值;
(2)若为第二象限角,且,求的值.
21.已知函数()的最小正周期为.
(1)求函数的单调增区间;
(2)将函数的图像向左平移个单位,再向上平移个单位,得到函数的图像.求在区间上零点的个数.
22.如图为函数的部分图象.
(1)求函数解析式;
(2)若方程在上有两个不相等的实数根,则实数的取值范围.
数学(文科)
参考答案
一:选择题
1.A
2.C
3.B
4.C
5.C
6.C
7.B
8.A
9.C
10.B
11.B
12.C
二:填空题
13.48
14.12
15.
16.④
三:解答题
17.(1)860(2)75,75,74.2
【解析】
试题分析:(1)根据频率分布直方图可求
( http: / / www.21cnjy.com )得成绩不低于60分的概率值,结合样本容量可求得相应的人数;(2)众数为出现的次数最多的数,中位数为由小到大排列后的位于中间的数,平均数为各组的频率与该组的频数成绩之和
试题解析:(1)成绩不低于60分所占的频率为:1-(0.004+0.010)
10=0.86
所以成绩不低于60分的人数估计值为:1000
0.86=860(人)
-----------5分
(2)众数估计值:75
------------6分
设中位数为x,则(x-70)
0.032=0.5-0.04-0.1-0.2,解得x=75
---------8分
平均数估计值:s----10分
考点:频率分布直方图
18.
(1)因为x==4,y==250,
则=4+1+1+4=10,
(xi-x)(yi-y)=(-2)×(-150)+(-1)×(-50)+1×50+2×150=700,
所以=
( http: / / www.21cnjy.com )==70,
=y-x=250-70×4=-30.
故所求的回归直线方程为=70x-30.
(2)由题意得70x-30≥600,即x≥=9,所以若该商场计划营销额不低于600万元,则至少要投入9万元的促销费用.
19.(1)
(2)
【解析】
试题分析:(1)本小题是古典概型问
( http: / / www.21cnjy.com )题,欲求出点P落在区域C:x2+y2≤10内的概率,只须求出满足:x2+y2≤10上的点P的坐标有多少个,再将求得的值与整个点P的坐标个数求比值即得.(2)本小题是几何概型问题,欲求豆子落在区域M上的概率,只须求出满足:“豆子落在区域M上的概率”的区域的面积,再将求得的面积值与整个区域C的面积求比值即得试题解析:(1)以0、2、4为横、纵坐标的点P有(0,0)、(0,2)、(0,4)、(2,0)、(2,2)、(2,4)、(4,0)、(4,2)、(4,4)共9个,而这些点中,落在区域C内的点有:(0,0)、(0,2)、(2,0)、(2,2)共4个,∴所求概率为P=.
(2)∵区域M的面积为4,而区域C的面积为10π,
∴所求概率为P==.
( http: / / www.21cnjy.com )
考点:古典概型概率与几何概型概率
20.(1);(2).
【解析】
试题分析:(1)根据三角恒等变换的公式,化简,即可求解当时,的值;(2)由,解得,进而求解的值.
试题解析:
.
(1).
(2),∴,
∵是第二象限角,∴,
∴.
考点:三角函数的化简求值.
21.(1)函数的单调增区间;(2)在上有个零点.
【解析】
试题分析:(1)先由三角函数的周期计算公式得到,从而可确定,将当成一个整体,由正弦函数的性质得到,解出的范围,写成区间即是所求函数的单调递增区间;(2)将函数的图像向左平移个单位,再向上平移1个单位,得到的图像,即,由正弦函数的图像与性质得到该函数在一个周期内函数零点的个数,而恰为个周期,从而可得在上零点的个数.
试题解析:(1)由周期为,得,得
由正弦函数的单调增区间得
,得
所以函数的单调增区间
(2)将函数的图像向左平移个单位,再向上平移1个单位
得到的图像,所以
令,得或
所以函数在每个周期上恰有两个零点,恰为个周期,故在上有个零点.
考点:1.三角函数的图像与性质;2.函数的零点.
22.(1);(2).
【解析】【试题分析】(1)依据题设借助函数的图像探求函数解析式中的参数;(2)画出函数的图像借助图形的直观探求参数的范围。
(1)由题中的图象知,
,
,即,所以,
根据五点作图法,令,得到,
因为,所以,
.
(2)由在上的图象知,当上有两个不同的实根.
点睛:本题以函数的图像为背景,设置了三道与正弦函数图像有关的问题,旨在考查形如的三角函数的图像与性质。求解第一问时,依据题设借助函数的图像中的数据信息探求出函数解析式中的参数;解答第二问时,画出函数的图像借助图形的直观探求参数使得问题获解。
同课章节目录
