陕西省黄陵中学高新部2016-2017学年高二下学期期中考试数学(文)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学高新部2016-2017学年高二下学期期中考试数学(文)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 303.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-07 20:37:44 | ||
图片预览



文档简介
黄陵中学高新部2016-2017学年度第二学期期中考试
高二文科数学
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下面说法:
①演绎推理是由一般到特殊的推理;②演绎推理得到的结论一定是正确的;③演绎推理的一般模式是“三段论”的形式;④演绎推理得到结论的正确与否与大前提、小前提和推理形式有关;⑤运用三段论推理时,大前提和小前提都不可以省略.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
2.“所有9的倍数都是3的倍数,某奇数是9的倍数,故某奇数是3的倍数.”上述推理是( )
A.小前提错
B.结论错
C.正确的
D.大前提错
3.推理过程“大前提:________,小前提:四边形ABCD是矩形.结论:四边形ABCD的对角线相等.”应补充的大前提是( )
A.正方形的对角线相等
B.矩形的对角线相等
C.等腰梯形的对角线相等
D.矩形的对边平行且相等
4.下图所示的是“概率”知识的( )
A.流程图
B.结构图
C.程序框图
D.直方图
5.有一段“三段论”,推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是函数f(x)=x3的极值点.以上推理中( )
A.大前提错误
B.小前提错误
C.推理形式错误
D.结论正确
6.用反证法证明“方程ax2+bx+c=0(a≠0)至多有两个解”的假设中,正确的是( )
A.至多有一个解
B.有且只有两个解
C.至少有三个解
D.至少有两个解
7.若a,b,c均为实数,则下面四个结论均是正确的:
①ab=ba;②(ab)c=a(bc);③若ab=bc,b≠0,则a-c=0;④若ab=0,则a=0或b=0.
对向量a,b,c,用类比的思想可得到以下四个结论:
①a·b=b·a;
②(a·b)c=a(b·c);
③若a·b=b·c,b≠0,则a=c;
④若a·b=0,则a=0或b=0.
其中结论正确的有( )
A.0个
B.1个
C.2个
D.3个
8.已知x>0,不等式x+≥2,x+≥3,x+≥4,…,可推广为x+≥n+1,则a的值为( )
A.n2
B.nn
C.2n
D.22n-2
9.下列各数中,纯虚数的个数是( )
2+,i,0i,5i+8,i(1-),0.618
A.0
B.1
C.2
D.3
10.下列命题中,正确命题的个数是( )
①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
A.0
B.1
C.2
D.3
11.根据调查,制作了一个城市消费结构图如下:
不属于市中心居民消费的是( )
A.新服装
B.家电
C.文化消费
D.服务消费
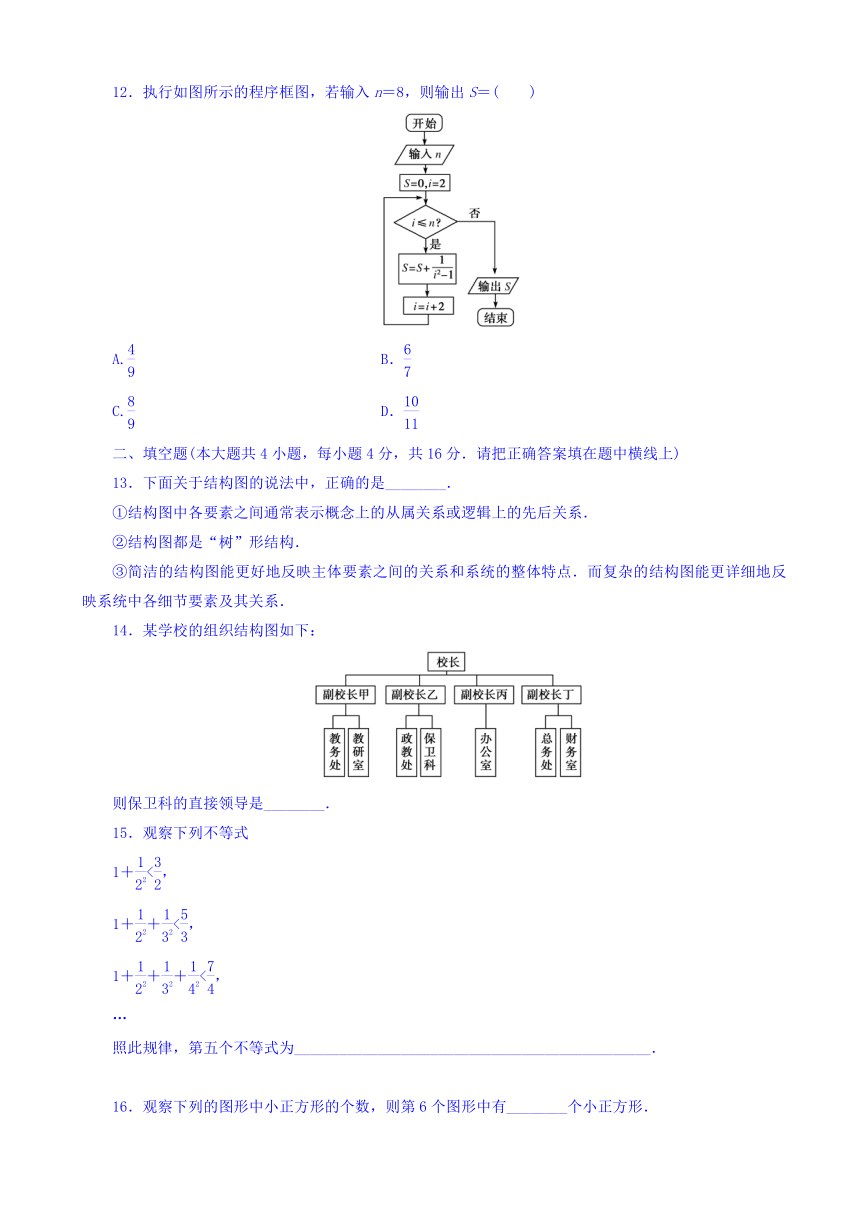
12.执行如图所示的程序框图,若输入n=8,则输出S=( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题4分,共16分.请把正确答案填在题中横线上)
13.下面关于结构图的说法中,正确的是________.
①结构图中各要素之间通常表示概念上的从属关系或逻辑上的先后关系.
②结构图都是“树”形结构.
③简洁的结构图能更好地反映主体要素之间的关系和系统的整体特点.而复杂的结构图能更详细地反映系统中各细节要素及其关系.
14.某学校的组织结构图如下:
则保卫科的直接领导是________.
15.观察下列不等式
1+<,
1++<,
1+++<,
…
照此规律,第五个不等式为_______________________________________________.
16.观察下列的图形中小正方形的个数,则第6个图形中有________个小正方形.
三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知非零实数a,b,c构成公差不为0的等差数列,求证:,,不能构成等差数列.
18.(本小题满分12分)中央电视台少儿频道主持人鞠萍,堪称一名节水高手.在一期节目中她谈到自己生活中的节水小窍门——做饭、淘米、洗菜的水留下来擦地或者浇花,洗衣服剩下的水留下冲卫生间.这样全家一个月节省消费10元多,一年下来就节省120多元.试用所学的框图知识表示她的节水过程.
19.(本小题满分12分)若a,b,c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+.求证:a,b,c中至少有一个大于0.
20.(本小题满分12分)观察下列各式:
1=1,1+=,1++=,1+++=,由上述等式能得到怎样的结论?写出结论并加以证明.
21.(本小题满分13分)某药厂生产某产品的工艺过程:
(1)备料、前处理、提取、制粒、压片、包衣、颗粒分装、包装.
(2)提取环节经检验,合格,进入下个工序,否则返回前处理.
(3)包衣、颗粒分装两环节检验合格进入下个工序,否则为废品.
画出生产该产品的工序流程图.
22.(本小题满分13分)满足z+是实数,且z+3的实部与虚部是相反数的虚数z是否存在?若存在,求出虚数z,若不存在,请说明理由.
答案
1.解析: ①③④都正确.
答案: C
2.解析: 演绎推理的结论不会超出前提所界定的范围,所以在演绎推理中,只要前提和推理形式正确,其结论就必然正确,故选C.
答案: C
3.解析: 由三段论的一般模式知应选B.
答案: B
4.解析: 这是关于“概率”的知识结构图.
答案: B
5.解析: 在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析其大前提的形式:“对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点”,不难得到结论.因为大前提是:“对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点”,不是真命题,因为对于可导函数f(x),如果f′(x0)=0,且满足当x>x0时和当x答案: A
6.解析: “至多n个”的反设应为“至少n+1个”.故选C.
答案: C
7.解析: 利用类比思想结合向量的定义及性质,特别是向量的数量积的定义可知①正确,②③④不正确.
答案: B
8解析: 由x+≥2,x+=x+≥3,x+=x+≥4,…,可推广为x+≥n+1,故a=nn.
答案: B
9.解析: 根据纯虚数的定义知,i,i(1-)是纯虚数.
答案: C
10.解析: ①由于x,y∈C,
所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,①是假命题.
②由于两个虚数不能比较大小,
∴②是假命题.
③当x=1,y=i时,x2+y2=0成立,
∴③是假命题.
答案: A
11.答案: B
12.解析: 运行一次后,S=0+=,i=4;运行两次后S=+=,i=6;运行三次后S=+=,i=8;运行四次后S=+=,i=10,10>8,不再循环,输出S.
答案: A
13.解析: 由结构图的功能知①③正确,结构图也可以是“环”形结构,②不正确.
答案: ①③
14.解析: 由结构图可知,保卫科的直接领导为副校长乙.
答案: 副校长乙
15.解析: 先观察左边,第一个不等式为2项相加,第二个不等式为3项相加,第三个不等式为4项相加,则第五个不等式应为6项相加,右边分子为分母的2倍减1,分母即为所对应项数,故应填1+++++<.
答案: 1+++++<16.解析: 第1个图中有3个小正方形,第2个有3+3=6个小正方形,第3个有6+4=10个小正方形,第4个图形有10+5=15个小正方形,第5个图形有15+6=21个小正方形,第6个图形中有21+7=28个小正方形.
16.答案: 28
17.证明: 假设,,能构成等差数列,则=+,
因此b(a+c)=2ac.
而由于a,b,c构成等差数列可得2b=a+c,
∴(a+c)2=4ac,即(a-c)2=0,于是得a=b=c,
这与a,b,c构成公差不为0的等差数列矛盾.
故假设不成立,即,,不能构成等差数列.
18.解析: 如下图所示:
19.证明: 假设a,b,c都不大于0,
即a≤0,b≤0,c≤0,
所以a+b+c≤0.
而a+b+c=++
=(x2-2x)+(y2-2y)+(z2-2z)+π
=(x-1)2+(y-1)2+(z-1)2+π-3.
所以a+b+c>0,这与a+b+c≤0矛盾,故a,b,c中至少有一个大于0
20.解析: 通过观察上面给出的各个式子,可以发现这些等式中蕴涵的基本规律,这个规律可以用一个等式来表示,即1+++…+
=(n∈N
).
这一结论的证明如下:
由于=
=2,
∴1+++…+
=2
=2=.
21.解析: 该产品的工序流程图:
22.解析: 存在.
设虚数z=x+yi(x,y∈R,且y≠0).
z+=x+yi+
=x++i.
由已知得,
∵y≠0,
∴,
解得或.
∴存在虚数z=-1-2i或z=-2-i满足以上条件.
高二文科数学
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.下面说法:
①演绎推理是由一般到特殊的推理;②演绎推理得到的结论一定是正确的;③演绎推理的一般模式是“三段论”的形式;④演绎推理得到结论的正确与否与大前提、小前提和推理形式有关;⑤运用三段论推理时,大前提和小前提都不可以省略.
其中正确的有( )
A.1个
B.2个
C.3个
D.4个
2.“所有9的倍数都是3的倍数,某奇数是9的倍数,故某奇数是3的倍数.”上述推理是( )
A.小前提错
B.结论错
C.正确的
D.大前提错
3.推理过程“大前提:________,小前提:四边形ABCD是矩形.结论:四边形ABCD的对角线相等.”应补充的大前提是( )
A.正方形的对角线相等
B.矩形的对角线相等
C.等腰梯形的对角线相等
D.矩形的对边平行且相等
4.下图所示的是“概率”知识的( )
A.流程图
B.结构图
C.程序框图
D.直方图
5.有一段“三段论”,推理是这样的:对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点,因为f(x)=x3在x=0处的导数值f′(0)=0,所以x=0是函数f(x)=x3的极值点.以上推理中( )
A.大前提错误
B.小前提错误
C.推理形式错误
D.结论正确
6.用反证法证明“方程ax2+bx+c=0(a≠0)至多有两个解”的假设中,正确的是( )
A.至多有一个解
B.有且只有两个解
C.至少有三个解
D.至少有两个解
7.若a,b,c均为实数,则下面四个结论均是正确的:
①ab=ba;②(ab)c=a(bc);③若ab=bc,b≠0,则a-c=0;④若ab=0,则a=0或b=0.
对向量a,b,c,用类比的思想可得到以下四个结论:
①a·b=b·a;
②(a·b)c=a(b·c);
③若a·b=b·c,b≠0,则a=c;
④若a·b=0,则a=0或b=0.
其中结论正确的有( )
A.0个
B.1个
C.2个
D.3个
8.已知x>0,不等式x+≥2,x+≥3,x+≥4,…,可推广为x+≥n+1,则a的值为( )
A.n2
B.nn
C.2n
D.22n-2
9.下列各数中,纯虚数的个数是( )
2+,i,0i,5i+8,i(1-),0.618
A.0
B.1
C.2
D.3
10.下列命题中,正确命题的个数是( )
①若x,y∈C,则x+yi=1+i的充要条件是x=y=1;
②若a,b∈R且a>b,则a+i>b+i;
③若x2+y2=0,则x=y=0.
A.0
B.1
C.2
D.3
11.根据调查,制作了一个城市消费结构图如下:
不属于市中心居民消费的是( )
A.新服装
B.家电
C.文化消费
D.服务消费
12.执行如图所示的程序框图,若输入n=8,则输出S=( )
A.
B.
C.
D.
二、填空题(本大题共4小题,每小题4分,共16分.请把正确答案填在题中横线上)
13.下面关于结构图的说法中,正确的是________.
①结构图中各要素之间通常表示概念上的从属关系或逻辑上的先后关系.
②结构图都是“树”形结构.
③简洁的结构图能更好地反映主体要素之间的关系和系统的整体特点.而复杂的结构图能更详细地反映系统中各细节要素及其关系.
14.某学校的组织结构图如下:
则保卫科的直接领导是________.
15.观察下列不等式
1+<,
1++<,
1+++<,
…
照此规律,第五个不等式为_______________________________________________.
16.观察下列的图形中小正方形的个数,则第6个图形中有________个小正方形.
三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)
17.(本小题满分12分)已知非零实数a,b,c构成公差不为0的等差数列,求证:,,不能构成等差数列.
18.(本小题满分12分)中央电视台少儿频道主持人鞠萍,堪称一名节水高手.在一期节目中她谈到自己生活中的节水小窍门——做饭、淘米、洗菜的水留下来擦地或者浇花,洗衣服剩下的水留下冲卫生间.这样全家一个月节省消费10元多,一年下来就节省120多元.试用所学的框图知识表示她的节水过程.
19.(本小题满分12分)若a,b,c均为实数,且a=x2-2y+,b=y2-2z+,c=z2-2x+.求证:a,b,c中至少有一个大于0.
20.(本小题满分12分)观察下列各式:
1=1,1+=,1++=,1+++=,由上述等式能得到怎样的结论?写出结论并加以证明.
21.(本小题满分13分)某药厂生产某产品的工艺过程:
(1)备料、前处理、提取、制粒、压片、包衣、颗粒分装、包装.
(2)提取环节经检验,合格,进入下个工序,否则返回前处理.
(3)包衣、颗粒分装两环节检验合格进入下个工序,否则为废品.
画出生产该产品的工序流程图.
22.(本小题满分13分)满足z+是实数,且z+3的实部与虚部是相反数的虚数z是否存在?若存在,求出虚数z,若不存在,请说明理由.
答案
1.解析: ①③④都正确.
答案: C
2.解析: 演绎推理的结论不会超出前提所界定的范围,所以在演绎推理中,只要前提和推理形式正确,其结论就必然正确,故选C.
答案: C
3.解析: 由三段论的一般模式知应选B.
答案: B
4.解析: 这是关于“概率”的知识结构图.
答案: B
5.解析: 在使用三段论推理证明中,如果命题是错误的,则可能是“大前提”错误,也可能是“小前提”错误,也可能是推理形式错误,我们分析其大前提的形式:“对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点”,不难得到结论.因为大前提是:“对于可导函数f(x),如果f′(x0)=0,那么x=x0是函数f(x)的极值点”,不是真命题,因为对于可导函数f(x),如果f′(x0)=0,且满足当x>x0时和当x
6.解析: “至多n个”的反设应为“至少n+1个”.故选C.
答案: C
7.解析: 利用类比思想结合向量的定义及性质,特别是向量的数量积的定义可知①正确,②③④不正确.
答案: B
8解析: 由x+≥2,x+=x+≥3,x+=x+≥4,…,可推广为x+≥n+1,故a=nn.
答案: B
9.解析: 根据纯虚数的定义知,i,i(1-)是纯虚数.
答案: C
10.解析: ①由于x,y∈C,
所以x+yi不一定是复数的代数形式,不符合复数相等的充要条件,①是假命题.
②由于两个虚数不能比较大小,
∴②是假命题.
③当x=1,y=i时,x2+y2=0成立,
∴③是假命题.
答案: A
11.答案: B
12.解析: 运行一次后,S=0+=,i=4;运行两次后S=+=,i=6;运行三次后S=+=,i=8;运行四次后S=+=,i=10,10>8,不再循环,输出S.
答案: A
13.解析: 由结构图的功能知①③正确,结构图也可以是“环”形结构,②不正确.
答案: ①③
14.解析: 由结构图可知,保卫科的直接领导为副校长乙.
答案: 副校长乙
15.解析: 先观察左边,第一个不等式为2项相加,第二个不等式为3项相加,第三个不等式为4项相加,则第五个不等式应为6项相加,右边分子为分母的2倍减1,分母即为所对应项数,故应填1+++++<.
答案: 1+++++<16.解析: 第1个图中有3个小正方形,第2个有3+3=6个小正方形,第3个有6+4=10个小正方形,第4个图形有10+5=15个小正方形,第5个图形有15+6=21个小正方形,第6个图形中有21+7=28个小正方形.
16.答案: 28
17.证明: 假设,,能构成等差数列,则=+,
因此b(a+c)=2ac.
而由于a,b,c构成等差数列可得2b=a+c,
∴(a+c)2=4ac,即(a-c)2=0,于是得a=b=c,
这与a,b,c构成公差不为0的等差数列矛盾.
故假设不成立,即,,不能构成等差数列.
18.解析: 如下图所示:
19.证明: 假设a,b,c都不大于0,
即a≤0,b≤0,c≤0,
所以a+b+c≤0.
而a+b+c=++
=(x2-2x)+(y2-2y)+(z2-2z)+π
=(x-1)2+(y-1)2+(z-1)2+π-3.
所以a+b+c>0,这与a+b+c≤0矛盾,故a,b,c中至少有一个大于0
20.解析: 通过观察上面给出的各个式子,可以发现这些等式中蕴涵的基本规律,这个规律可以用一个等式来表示,即1+++…+
=(n∈N
).
这一结论的证明如下:
由于=
=2,
∴1+++…+
=2
=2=.
21.解析: 该产品的工序流程图:
22.解析: 存在.
设虚数z=x+yi(x,y∈R,且y≠0).
z+=x+yi+
=x++i.
由已知得,
∵y≠0,
∴,
解得或.
∴存在虚数z=-1-2i或z=-2-i满足以上条件.
同课章节目录
