陕西省黄陵中学2016-2017学年高二(重点班)下学期期中考试数学(理)试题 Word版含答案
文档属性
| 名称 | 陕西省黄陵中学2016-2017学年高二(重点班)下学期期中考试数学(理)试题 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 196.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-07 21:22:11 | ||
图片预览


文档简介
高二重点班期中考试理科数学
一、选择题(每小题5分,共60分)
1.向量=(2,-3)对应的复数为( )
A.z=2-3i
B.z=2+3i
C.z=3+2i
D.z=-3-2i
2.已知0<a<2,复数z=a+i(i是虚数单位),则|z|的取值范围是( )
A.(1,)
B.(1,)
C.(1,3)
D.(1,5)
3.在复平面内,向量对应的复数是2+i,向量对应的复数是-1-3i,则向量对应的复数为( )
A.1-2i
B.-1+2i
C.3+4i
D.-3-4i
4.若复数z1=1+5i,z2=-3+7i,则复数z=z1-z2在复平面内对应的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.设z1=2+bi,z2=a+i,当z1+z2=0时,复数a+bi为( )
A.1+i
B.2+i
C.3
D.-2-i
6.设向量,,对应的复数分别为z1,z2,z3,那么( )
A.z1+z2+z3=0
B.z1-z2-z3=0
C.z1-z2+z3=0
D.z1+z2-z3=0
7.复数z=(a2-1)+(a2-a-6)i对应的点在第四象限,则实数a的取值范围是( )
A.(-2,-1)
B.(1,3)
C.(-2,-1)∪(-1,3)
D.(-2,-1)∪(1,3)
8.设复数z=(3-4i)(1+2i)(i是虚数单位),则复数z的虚部为( )
A.-2
B.2
C.-2i
D.2i
9.已知复数z=i(1+i)(i为虚数单位),则复数z在复平面上所对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.复数=( )
A.2-i
B.1-2i
C.-2+i
D.-1+2i
11.流程图描述动态过程,关于其“终点”的描述,较为恰当的是( )
A.只允许有一个“终点”
B.只允许有两个“终点”
C.可以有一个或多个“终点”
D.以上皆不正确
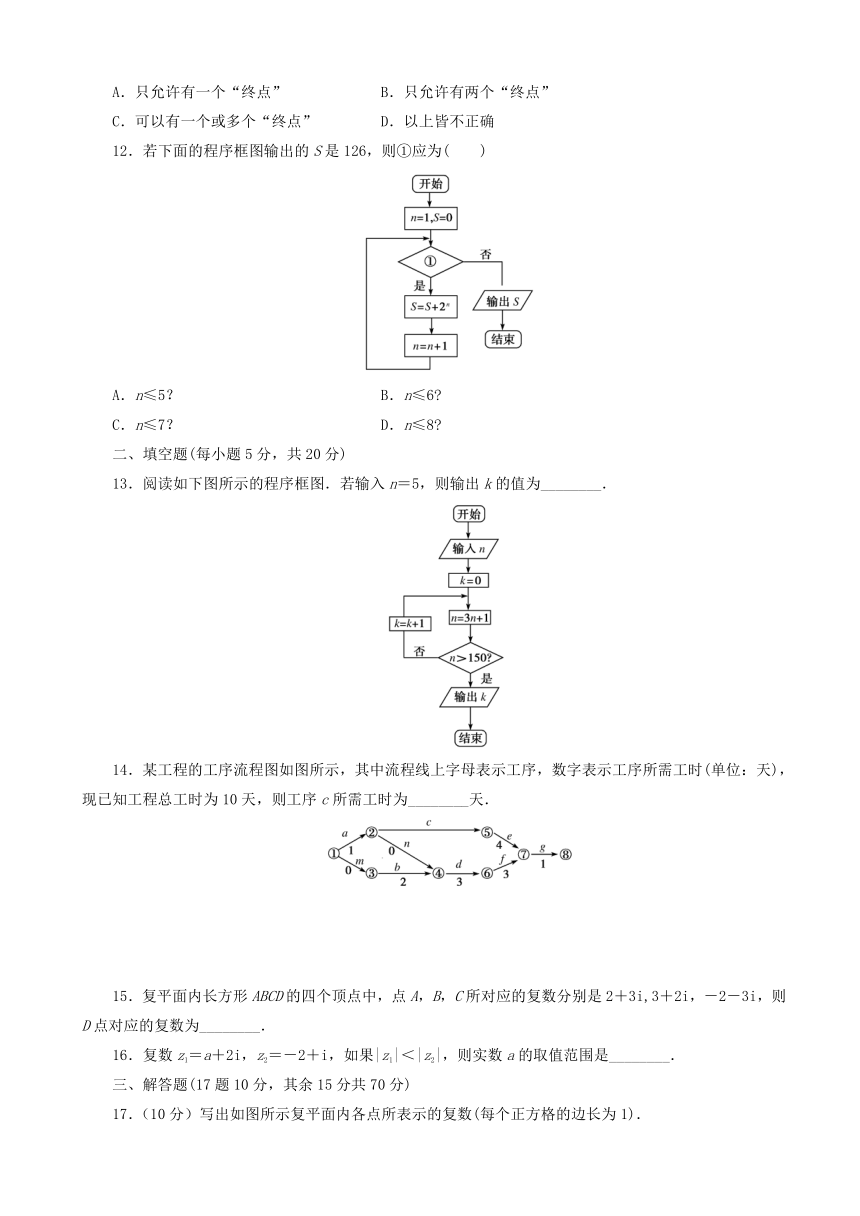
12.若下面的程序框图输出的S是126,则①应为( )
A.n≤5?
B.n≤6
C.n≤7?
D.n≤8
二、填空题(每小题5分,共20分)
13.阅读如下图所示的程序框图.若输入n=5,则输出k的值为________.
14.某工程的工序流程图如图所示,其中流程线上字母表示工序,数字表示工序所需工时(单位:天),现已知工程总工时为10天,则工序c所需工时为________天.
15.复平面内长方形ABCD的四个顶点中,点A,B,C所对应的复数分别是2+3i,3+2i,-2-3i,则D点对应的复数为________.
16.复数z1=a+2i,z2=-2+i,如果|z1|<|z2|,则实数a的取值范围是________.
三、解答题(17题10分,其余15分共70分)
17.(10分)写出如图所示复平面内各点所表示的复数(每个正方格的边长为1).
18.已知m∈R,复数z=+(m2+2m-3)i.则当m为何值时,
(1)z∈R
(2)z是纯虚数?
(3)z对应的点位于复平面第二象限?
(4)z对应的点在直线x+y+3=0上?
19.满足z+是实数,且z+3的实部与虚部是相反数的虚数z是否存在?若存在,求出虚数z,若不存在,请说明理由.
20.已知z1=cos
θ+isin
θ,z2=cos
α+isin
α(θ,α∈R),求|z1+z2|的取值范围.
21.已知数列{an}的前n项和Sn=1+λan.其中λ≠0.
(1)证明{an}是等比数列,并求其通项公式;
(2)若S3=,求λ.
参考答案
1解析: 因为相等的向量对应的复数相等,与向量=(2,-3)相等的向量是=(2,-3),而向量=(2,-3)对应的复数是z=2-3i,所以向量=(2,-3)对应的复数是z=2-3i.
答案: A
2解析: |z|=.∵0<a<2,
∴1<a2+1<5,∴|z|∈(1,).
答案: B
3解析: 由题意知=(2,1),=(-1,-3).
=+=(-1,-3)+(-2,-1)=(-3,-4),
∴对应的复数为-3-4i.
答案: D
4解析: z=z1-z2=(1+5i)-(-3+7i)=4-2i.
答案: D
5解析: 由z1+z2=0,得解得故选D.
答案: D
6解析: ∵+-=-=0.∴z1+z2-z3=0.
答案: D
7解析: 复数z=(a2-1)+(a2-a-6)i对应的点的坐标为(a2-1,a2-a-6),据题意有
解得-2答案: D
8解析: 由z=(3-4i)(1+2i)=11+2i,所以复数z的虚部为2.
答案: B
9解析: 因为z=i(1+i)=-1+i,所以z在复平面上对应的点位于第二象限.
答案: B
10解析: ===-2+i.
答案: C
11解析: 流程图有一个“起点”,但可以有一个或多个“终点”,故选C.
答案: C
12解析: 由循环体可知:0+21+22+23+24+25+26=126.
答案: B
13.解析: 执行程序框图可得n=5,k=0;n=16,k=1;n=49,k=2;n=148,k=3;n=148×3+1>150,循环结束,故输出的k值为3.
答案: 3
14解析: 由工序流程图可知a,c,e,g是一个完整的工程流程,且工序a所需工时为1天,工序e所需工时为4天,工序g所需工时为1天,已知工程总工时为10天,故工序c所需工时为4天.
答案: 4
15解析: 由题意可知A(2,3),B(3,2),C(-2,-3),设D(x,y),则=,即(x-2,y-3)=(-5,-5),解得
故D点对应的复数为-3-2i.
答案: -3-2i
16解析: ∵|z1|=,|z2|=,
∴<,∴-1<a<1.
答案: (-1,1)
17解析: 如题图所示,点A的坐标为(4,3),
则点A对应的复数为4+3i.
同理可知点B,C,F,G,H,O对应的复数分别为:
3-3i,-3+2i,-2,5i,-5i,0.
18解析: 复数z=a+bi(a,b∈R),当且仅当b=0时,z∈R;当且仅当a=0且b≠0时,z为纯虚数;当a<0,b>0时,z对应的点位于复平面的第二象限;复数z对应的点的坐标是直线方程的解,则这个点就在这条直线上.
(1)由m2+2m-3=0且m-1≠0,得m=-3.故当m=-3时,z∈R.
(2)由
解得m=0,或m=-2.
故当m=0,或m=-2时,z为纯虚数.
(3)由解得m<-3.
故当m<-3时,z对应的点位于复平面的第二象限.
(4)由+(m2+2m-3)+3=0,
解得m=0或m=-2.
故当m=0或m=-2时,z对应的点在直线x+y+3=0上.
19解析: 存在.
设虚数z=x+yi(x,y∈R,且y≠0).
z+=x+yi+
=x++i.
由已知得,
∵y≠0,
∴,
解得或.
∴存在虚数z=-1-2i或z=-2-i满足以上条件.
20解析: 方法一:∵z1+z2=cos
θ+isin
θ+cos
α+isin
α
=(cos
θ+cos
α)+i(sin
θ+sin
α),
∴|z1+z2|2=(cos
θ+cos
α)2+(sin
θ+sin
α)2
=2+2(cos
θcos
α+sin
θsin
α)=2+2cos(θ-α),
由于(2+2cos(θ-α))∈[0,4],
∴|z1+z2|∈[0,2].
方法二:∵|z1|=|z2|=1,
又||z1|-|z2||≤|z1+z2|≤|z1|+|z2|,
∴0≤|z1+z2|≤2,即|z1+z2|∈[0,2].
21[解析] (1)由题意得a1=S1=1+λa1,
故λ≠1,a1=,a1≠0.
由Sn=1+λan,Sn+1=1+λan+1得an+1=λan+1-λan,
即an+1(λ-1)=λan.
由a1≠0,λ≠0且λ≠1得an≠0,
所以=.
因此{an}是首项为,公比为的等比数列,
于是an=()n-1.
(2)由(1)得Sn=1-()n.
由S5=得1-()5=,即()5=.
解得λ=-1.
一、选择题(每小题5分,共60分)
1.向量=(2,-3)对应的复数为( )
A.z=2-3i
B.z=2+3i
C.z=3+2i
D.z=-3-2i
2.已知0<a<2,复数z=a+i(i是虚数单位),则|z|的取值范围是( )
A.(1,)
B.(1,)
C.(1,3)
D.(1,5)
3.在复平面内,向量对应的复数是2+i,向量对应的复数是-1-3i,则向量对应的复数为( )
A.1-2i
B.-1+2i
C.3+4i
D.-3-4i
4.若复数z1=1+5i,z2=-3+7i,则复数z=z1-z2在复平面内对应的点在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.设z1=2+bi,z2=a+i,当z1+z2=0时,复数a+bi为( )
A.1+i
B.2+i
C.3
D.-2-i
6.设向量,,对应的复数分别为z1,z2,z3,那么( )
A.z1+z2+z3=0
B.z1-z2-z3=0
C.z1-z2+z3=0
D.z1+z2-z3=0
7.复数z=(a2-1)+(a2-a-6)i对应的点在第四象限,则实数a的取值范围是( )
A.(-2,-1)
B.(1,3)
C.(-2,-1)∪(-1,3)
D.(-2,-1)∪(1,3)
8.设复数z=(3-4i)(1+2i)(i是虚数单位),则复数z的虚部为( )
A.-2
B.2
C.-2i
D.2i
9.已知复数z=i(1+i)(i为虚数单位),则复数z在复平面上所对应的点位于( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
10.复数=( )
A.2-i
B.1-2i
C.-2+i
D.-1+2i
11.流程图描述动态过程,关于其“终点”的描述,较为恰当的是( )
A.只允许有一个“终点”
B.只允许有两个“终点”
C.可以有一个或多个“终点”
D.以上皆不正确
12.若下面的程序框图输出的S是126,则①应为( )
A.n≤5?
B.n≤6
C.n≤7?
D.n≤8
二、填空题(每小题5分,共20分)
13.阅读如下图所示的程序框图.若输入n=5,则输出k的值为________.
14.某工程的工序流程图如图所示,其中流程线上字母表示工序,数字表示工序所需工时(单位:天),现已知工程总工时为10天,则工序c所需工时为________天.
15.复平面内长方形ABCD的四个顶点中,点A,B,C所对应的复数分别是2+3i,3+2i,-2-3i,则D点对应的复数为________.
16.复数z1=a+2i,z2=-2+i,如果|z1|<|z2|,则实数a的取值范围是________.
三、解答题(17题10分,其余15分共70分)
17.(10分)写出如图所示复平面内各点所表示的复数(每个正方格的边长为1).
18.已知m∈R,复数z=+(m2+2m-3)i.则当m为何值时,
(1)z∈R
(2)z是纯虚数?
(3)z对应的点位于复平面第二象限?
(4)z对应的点在直线x+y+3=0上?
19.满足z+是实数,且z+3的实部与虚部是相反数的虚数z是否存在?若存在,求出虚数z,若不存在,请说明理由.
20.已知z1=cos
θ+isin
θ,z2=cos
α+isin
α(θ,α∈R),求|z1+z2|的取值范围.
21.已知数列{an}的前n项和Sn=1+λan.其中λ≠0.
(1)证明{an}是等比数列,并求其通项公式;
(2)若S3=,求λ.
参考答案
1解析: 因为相等的向量对应的复数相等,与向量=(2,-3)相等的向量是=(2,-3),而向量=(2,-3)对应的复数是z=2-3i,所以向量=(2,-3)对应的复数是z=2-3i.
答案: A
2解析: |z|=.∵0<a<2,
∴1<a2+1<5,∴|z|∈(1,).
答案: B
3解析: 由题意知=(2,1),=(-1,-3).
=+=(-1,-3)+(-2,-1)=(-3,-4),
∴对应的复数为-3-4i.
答案: D
4解析: z=z1-z2=(1+5i)-(-3+7i)=4-2i.
答案: D
5解析: 由z1+z2=0,得解得故选D.
答案: D
6解析: ∵+-=-=0.∴z1+z2-z3=0.
答案: D
7解析: 复数z=(a2-1)+(a2-a-6)i对应的点的坐标为(a2-1,a2-a-6),据题意有
解得-2
8解析: 由z=(3-4i)(1+2i)=11+2i,所以复数z的虚部为2.
答案: B
9解析: 因为z=i(1+i)=-1+i,所以z在复平面上对应的点位于第二象限.
答案: B
10解析: ===-2+i.
答案: C
11解析: 流程图有一个“起点”,但可以有一个或多个“终点”,故选C.
答案: C
12解析: 由循环体可知:0+21+22+23+24+25+26=126.
答案: B
13.解析: 执行程序框图可得n=5,k=0;n=16,k=1;n=49,k=2;n=148,k=3;n=148×3+1>150,循环结束,故输出的k值为3.
答案: 3
14解析: 由工序流程图可知a,c,e,g是一个完整的工程流程,且工序a所需工时为1天,工序e所需工时为4天,工序g所需工时为1天,已知工程总工时为10天,故工序c所需工时为4天.
答案: 4
15解析: 由题意可知A(2,3),B(3,2),C(-2,-3),设D(x,y),则=,即(x-2,y-3)=(-5,-5),解得
故D点对应的复数为-3-2i.
答案: -3-2i
16解析: ∵|z1|=,|z2|=,
∴<,∴-1<a<1.
答案: (-1,1)
17解析: 如题图所示,点A的坐标为(4,3),
则点A对应的复数为4+3i.
同理可知点B,C,F,G,H,O对应的复数分别为:
3-3i,-3+2i,-2,5i,-5i,0.
18解析: 复数z=a+bi(a,b∈R),当且仅当b=0时,z∈R;当且仅当a=0且b≠0时,z为纯虚数;当a<0,b>0时,z对应的点位于复平面的第二象限;复数z对应的点的坐标是直线方程的解,则这个点就在这条直线上.
(1)由m2+2m-3=0且m-1≠0,得m=-3.故当m=-3时,z∈R.
(2)由
解得m=0,或m=-2.
故当m=0,或m=-2时,z为纯虚数.
(3)由解得m<-3.
故当m<-3时,z对应的点位于复平面的第二象限.
(4)由+(m2+2m-3)+3=0,
解得m=0或m=-2.
故当m=0或m=-2时,z对应的点在直线x+y+3=0上.
19解析: 存在.
设虚数z=x+yi(x,y∈R,且y≠0).
z+=x+yi+
=x++i.
由已知得,
∵y≠0,
∴,
解得或.
∴存在虚数z=-1-2i或z=-2-i满足以上条件.
20解析: 方法一:∵z1+z2=cos
θ+isin
θ+cos
α+isin
α
=(cos
θ+cos
α)+i(sin
θ+sin
α),
∴|z1+z2|2=(cos
θ+cos
α)2+(sin
θ+sin
α)2
=2+2(cos
θcos
α+sin
θsin
α)=2+2cos(θ-α),
由于(2+2cos(θ-α))∈[0,4],
∴|z1+z2|∈[0,2].
方法二:∵|z1|=|z2|=1,
又||z1|-|z2||≤|z1+z2|≤|z1|+|z2|,
∴0≤|z1+z2|≤2,即|z1+z2|∈[0,2].
21[解析] (1)由题意得a1=S1=1+λa1,
故λ≠1,a1=,a1≠0.
由Sn=1+λan,Sn+1=1+λan+1得an+1=λan+1-λan,
即an+1(λ-1)=λan.
由a1≠0,λ≠0且λ≠1得an≠0,
所以=.
因此{an}是首项为,公比为的等比数列,
于是an=()n-1.
(2)由(1)得Sn=1-()n.
由S5=得1-()5=,即()5=.
解得λ=-1.
同课章节目录
