3.1图形的平移同步练习（解析版）

3.1图形的平移同步练习
一、单选题（共8题）
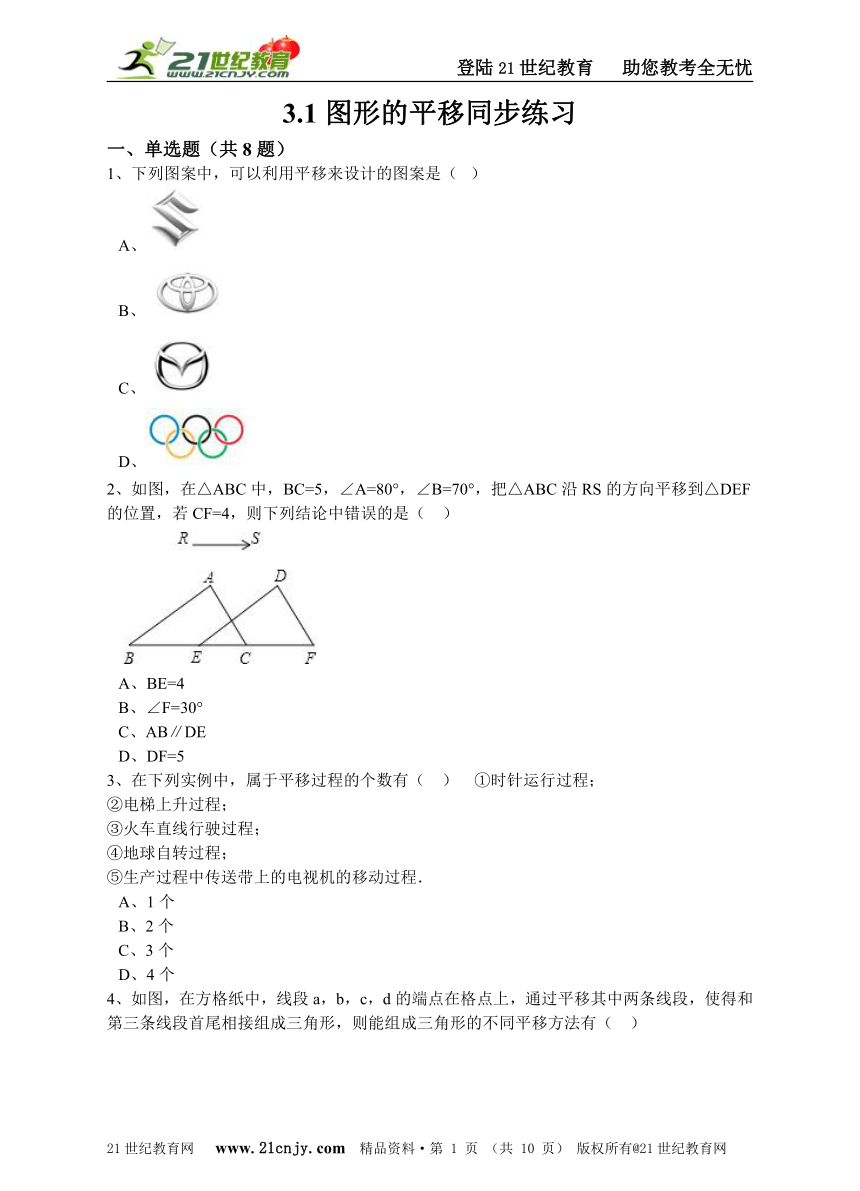
1、下列图案中，可以利用平移来设计的图案是（? ）
A、B、C、D、
2、如图，在△ABC中，BC=5，∠A=80°，∠B=70°，把△ABC沿RS的方向平移到△DEF的位置，若CF=4，则下列结论中错误的是（?? ）

A、BE=4B、∠F=30°C、AB∥DED、DF=5
3、在下列实例中，属于平移过程的个数有（?? ） ①时针运行过程；②电梯上升过程；③火车直线行驶过程；④地球自转过程；⑤生产过程中传送带上的电视机的移动过程．
A、1个B、2个C、3个D、4个
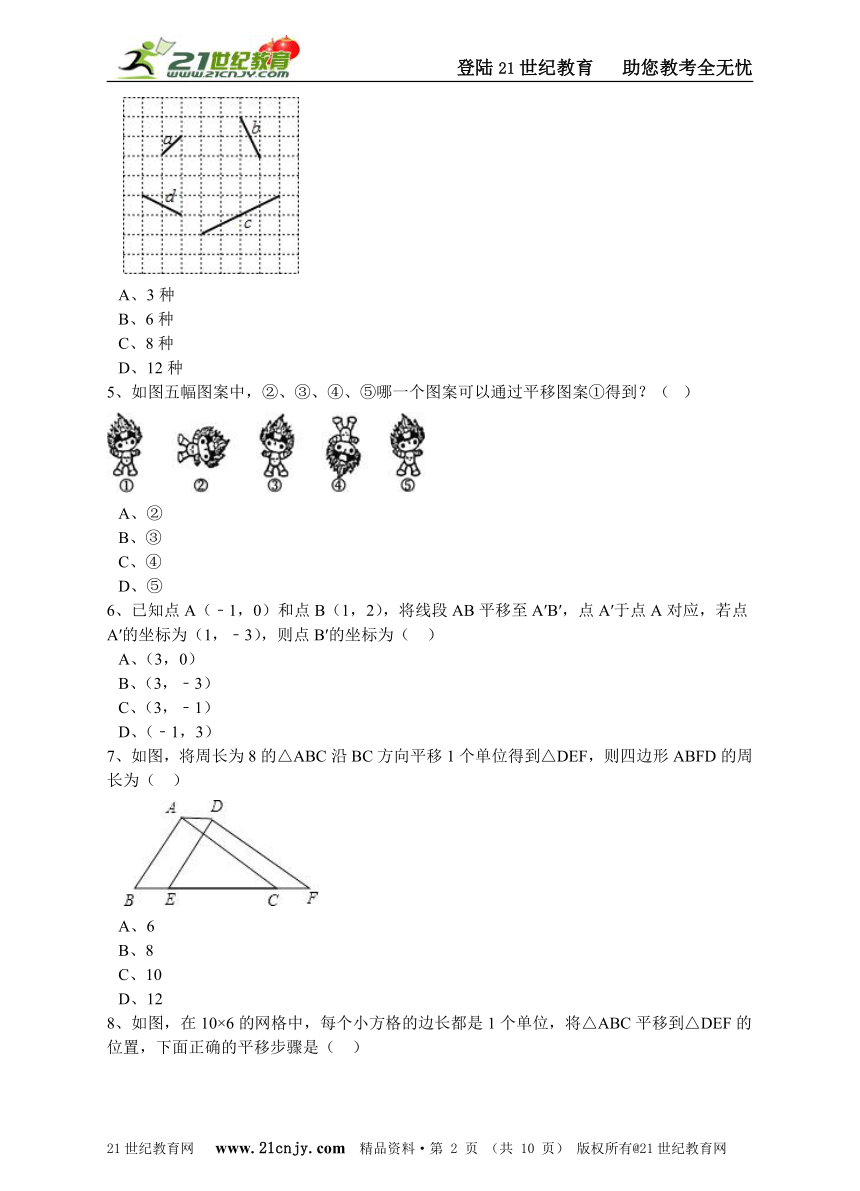
4、如图，在方格纸中，线段a，b，c，d的端点在格点上，通过平移其中两条线段，使得和第三条线段首尾相接组成三角形，则能组成三角形的不同平移方法有（?? ）

A、3种B、6种C、8种D、12种
5、如图五幅图案中，②、③、④、⑤哪一个图案可以通过平移图案①得到？（? ）
A、②B、③C、④D、⑤
6、已知点A（﹣1，0）和点B（1，2），将线段AB平移至A′B′，点A′于点A对应，若点A′的坐标为（1，﹣3），则点B′的坐标为（?? ） 21·世纪*教育网
A、（3，0）B、（3，﹣3）C、（3，﹣1）D、（﹣1，3）
7、如图，将周长为8的△ABC沿BC方向平移1个单位得到△DEF，则四边形ABFD的周长为（?? ）www-2-1-cnjy-com

A、6B、8C、10D、12
8、如图，在10×6的网格中，每个小方格的边长都是1个单位，将△ABC平移到△DEF的位置，下面正确的平移步骤是（?? ）【版权所有：21教育】
A、先向左平移5个单位，再向下平移2个单位B、先向右平移5个单位，再向下平移2个单位C、先向左平移5个单位，再向上平移2个单位D、先向右平移5个单位，再向下平移2个单位
二、填空题（共5题）
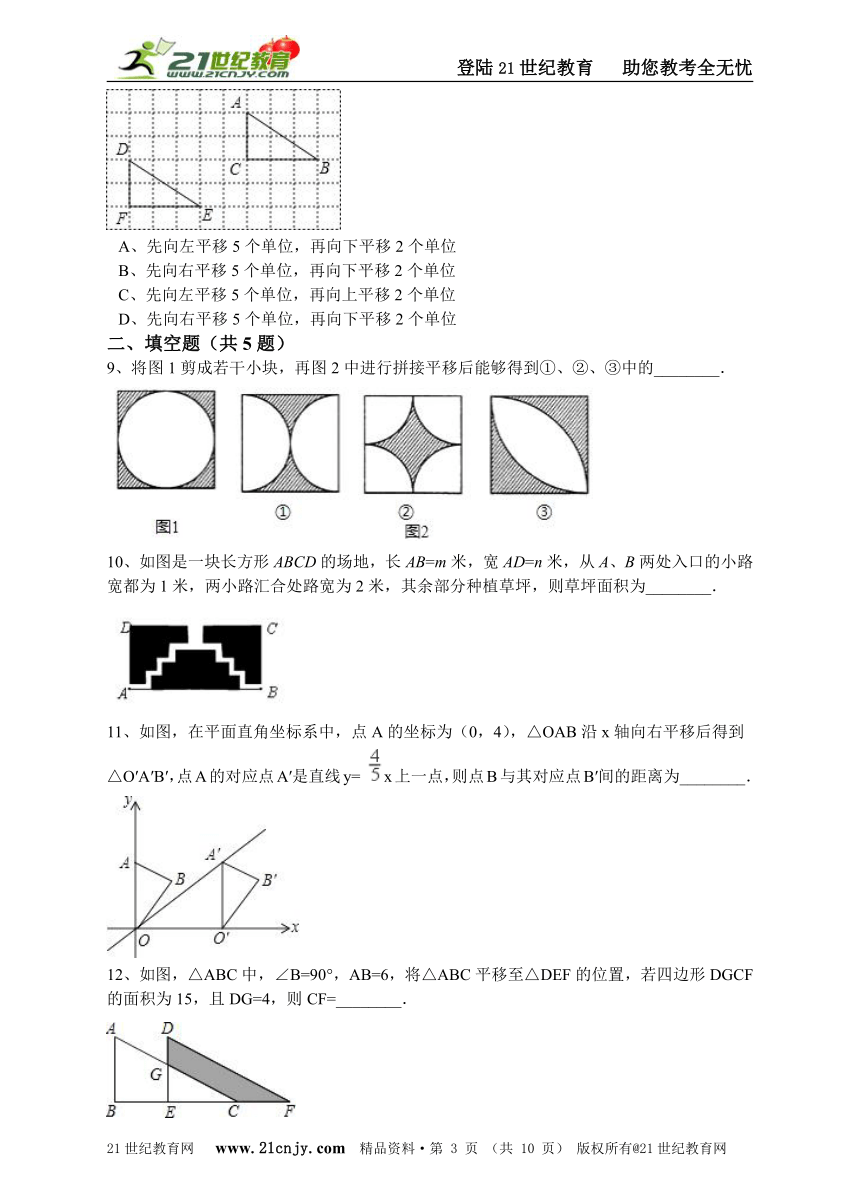
9、将图1剪成若干小块，再图2中进行拼接平移后能够得到①、②、③中的________．

10、如图是一块长方形ABCD的场地，长AB=m米，宽AD=n米，从A、B两处入口的小路宽都为1米，两小路汇合处路宽为2米，其余部分种植草坪，则草坪面积为________．
11、如图，在平面直角坐标系中，点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，点A的对应点A′是直线y= x上一点，则点B与其对应点B′间的距离为________．
12、如图，△ABC中，∠B=90°，AB=6，将△ABC平移至△DEF的位置，若四边形DGCF的面积为15，且DG=4，则CF=________．【来源：21cnj*y.co*m】
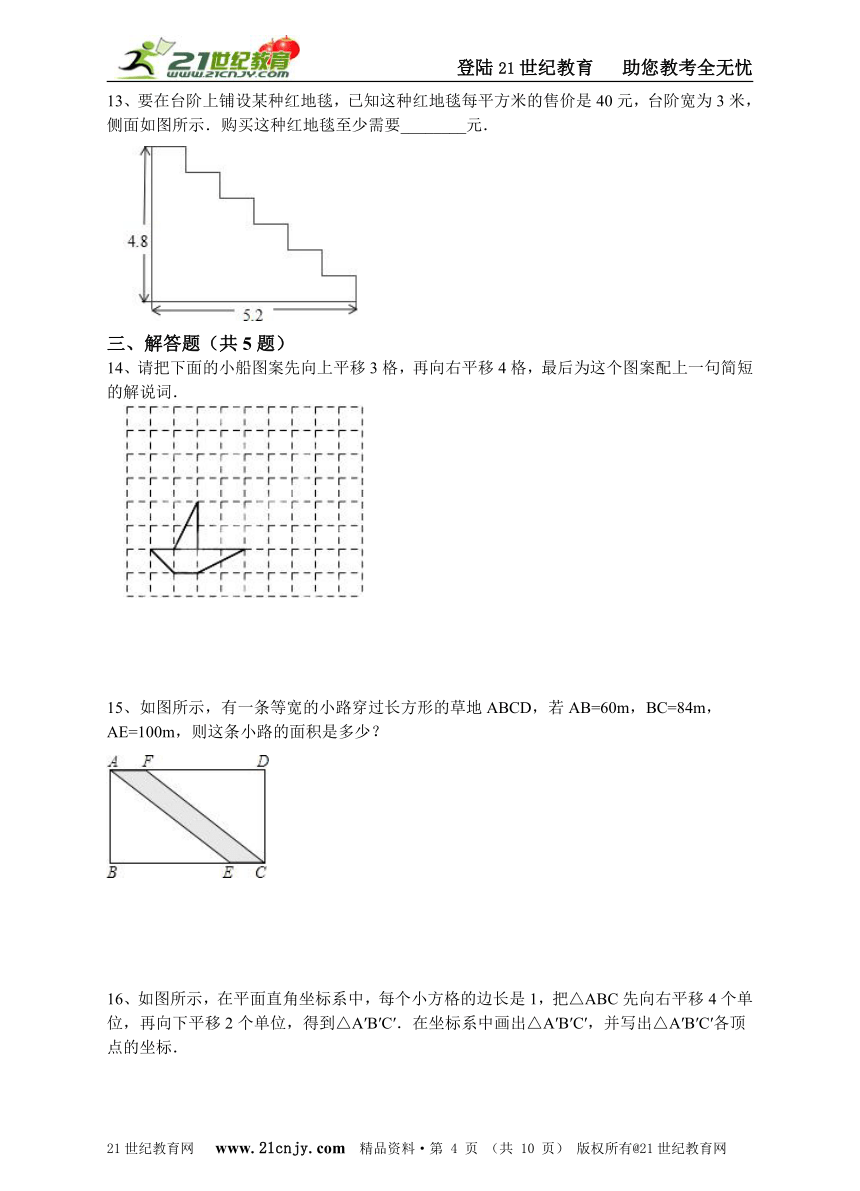
13、要在台阶上铺设某种红地毯，已知这种红地毯每平方米的售价是40元，台阶宽为3米，侧面如图所示．购买这种红地毯至少需要________元．21*cnjy*com

三、解答题（共5题）
14、请把下面的小船图案先向上平移3格，再向右平移4格，最后为这个图案配上一句简短的解说词．

如图所示，有一条等宽的小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，则这条小路的面积是多少？
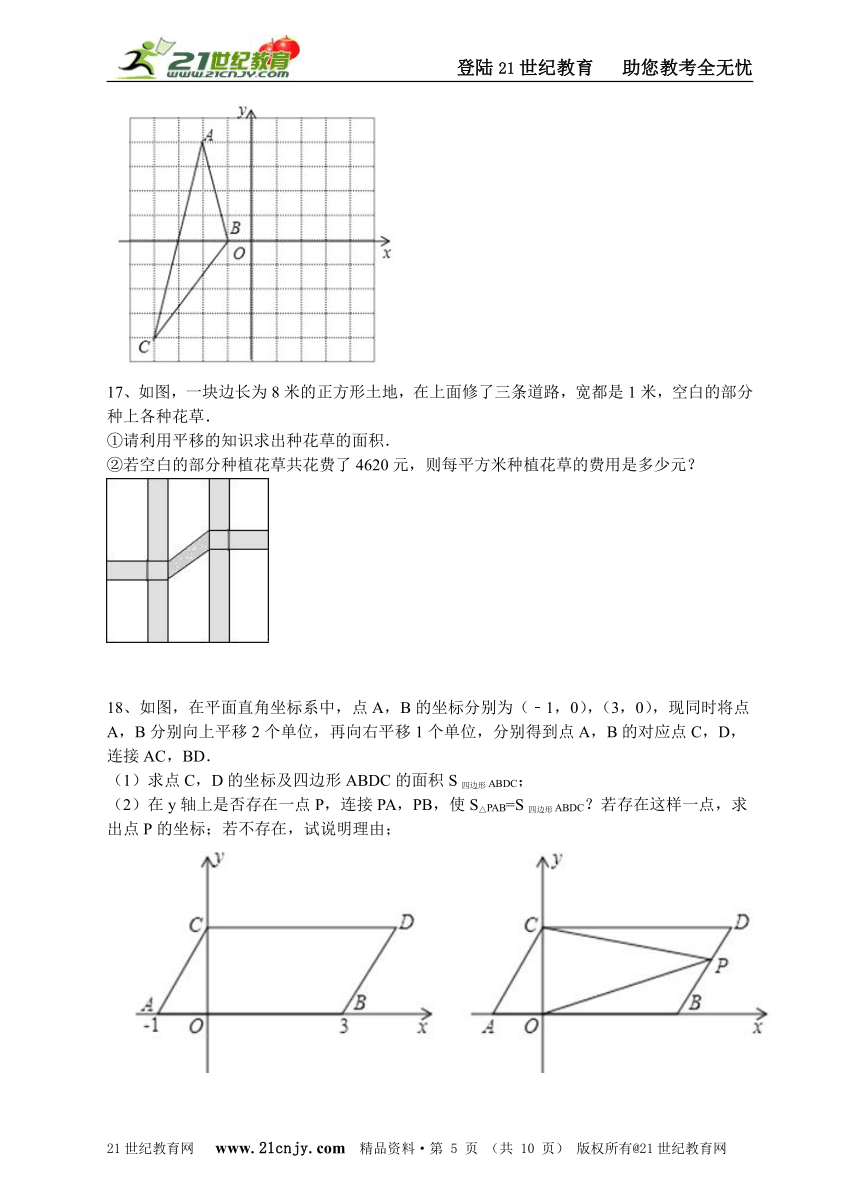
16、如图所示，在平面直角坐标系中，每个小方格的边长是1，把△ABC先向右平移4个单位，再向下平移2个单位，得到△A′B′C′．在坐标系中画出△A′B′C′，并写出△A′B′C′各顶点的坐标．
17、如图，一块边长为8米的正方形土地，在上面修了三条道路，宽都是1米，空白的部分种上各种花草．①请利用平移的知识求出种花草的面积．②若空白的部分种植花草共花费了4620元，则每平方米种植花草的费用是多少元？21教育网
18、如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD．（1）求点C，D的坐标及四边形ABDC的面积S四边形ABDC；（2）在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在这样一点，求出点P的坐标；若不存在，试说明理由；
答案解析
一、单选题
1、D 解：A、是利用中心对称设计的，不合题意； B，C是利用轴对称设计的，不合题意；D、是利用平移设计的，符合题意．故选：D． 21·cn·jy·com

3、C 解：①时针运行是旋转，故此选项错误； ②电梯上升，是平移现象；③火车直线行驶，是平移现象；④地球自转，是旋转现象；⑤电视机在传送带上运动，是平移现象．故属于平移变换的个数有3个．故选：C． 2·1·c·n·j·y
4、B 解：由网格可知：a= ，b=d= ，c=2 ， 则能组成三角形的只有：a，b，d可以分别通过平移ab，ad，bd得到三角形，平移其中两条线段方法有两种，即能组成三角形的不同平移方法有6种．故选：B．www.21-cn-jy.com
5、D 解：A、图案①到图案②属于旋转变换，故错误； B、图案①到图案③属于旋转变换，故错误；C、图案①到图案④属于旋转变换，故错误；D、图案①到图案⑤形状与大小没有改变，符合平移性质，故正确；故选：D． 【来源：21·世纪·教育·网】
6、C 解：∵A（﹣1，0）平移后对应点A′的坐标为（1，﹣3），∴A点的平移方法是：先向右平移2个单位，再向下平移3个单位，∴B点的平移方法与A点的平移方法是相同的，∴B（1，2）平移后B′的坐标是：（3，﹣1）．故选：C．【出处：21教育名师】
7、C 解：根据题意，将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF， ∴AD=1，BF=BC+CF=BC+1，DF=AC；又∵AB+BC+AC=8，∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10．故选：C．
8、A 解：根据网格结构，观察对应点A、D，点A向左平移5个单位，再向下平移2个单位即可到达点D的位置，所以平移步骤是：先把△ABC向左平移5个单位，再向下平移2个单位．故选：A．21世纪教育网版权所有
二、填空题
9、①② 解：根据图形1可得剪成若干小块，再图2中进行拼接平移后能够得到①、②，不能拼成③， 故答案为：①②． 21教育名师原创作品
10、40 解：由图可知：矩形ABCD中去掉小路后，草坪正好可以拼成一个新的矩形，且它的长为：（m-2）米，宽为（n-1）米．所以草坪的面积应该是长×宽=（m-2）（n-1）故答案为（m-2）（n-1）．
11、5 解：如图，连接AA′、BB′．∵点A的坐标为（0，4），△OAB沿x轴向右平移后得到△O′A′B′，∴点A′的纵坐标是4．又∵点A的对应点在直线y= x上一点，∴4= x，解得x=5．∴点A′的坐标是（5，4），∴AA′=5．∴根据平移的性质知BB′=AA′=5．故答案为：5．
12、解：根据题意得，DE=AB=6；设BE=CF=x，∵CH∥DF．∴EG=6﹣4=2；EG：GD=EC：CF，即 2：4=EC：x，∴EC= x，∴EF=EC+CF= x，∴S△EFD= × x×6= x；S△ECG= ×2× x= x．∴S阴影部分= x﹣ x=15．解得：x= ．故答案为 ．
13、1200 解：利用平移线段，把楼梯的横竖向上向右平移，构成一个矩形，长宽分别为5.2米，4.8米， ∴地毯的长度为5.2+4.8=10米，地毯的面积为10×3=30平方米，∴购买这种红地毯至少需要30×40=1200元．故答案为：1200． 21*cnjy*com
三、解答题
14、解：如图所示：
解说词：两只小船在水中向前滑行
解：路等宽，得BE=DF， △ABE≌△CDF，由勾股定理，得BE= =80（m）S△ABE=60×80÷2=2400（m2）路的面积=矩形的面积﹣两个三角形的面积=84×60﹣2400×2=240（m2）．答：这条小路的面积是240m2 ． 2-1-c-n-j-y
16、解：△A′B′C′如图所示；?A'（2，2）；B'（3，﹣2）；C'（0，﹣6）．
17、解：①（8－2）×（8－1）＝6×7＝42?（米2）答：种花草的面积为42米2 ． ②4620÷42＝110（元）答：每平方米种植花草的费用是110元． 21cnjy.com