3.2图形的旋转同步练习（解析版）

3.2图形的旋转同步练习
一、单选题（共8题）
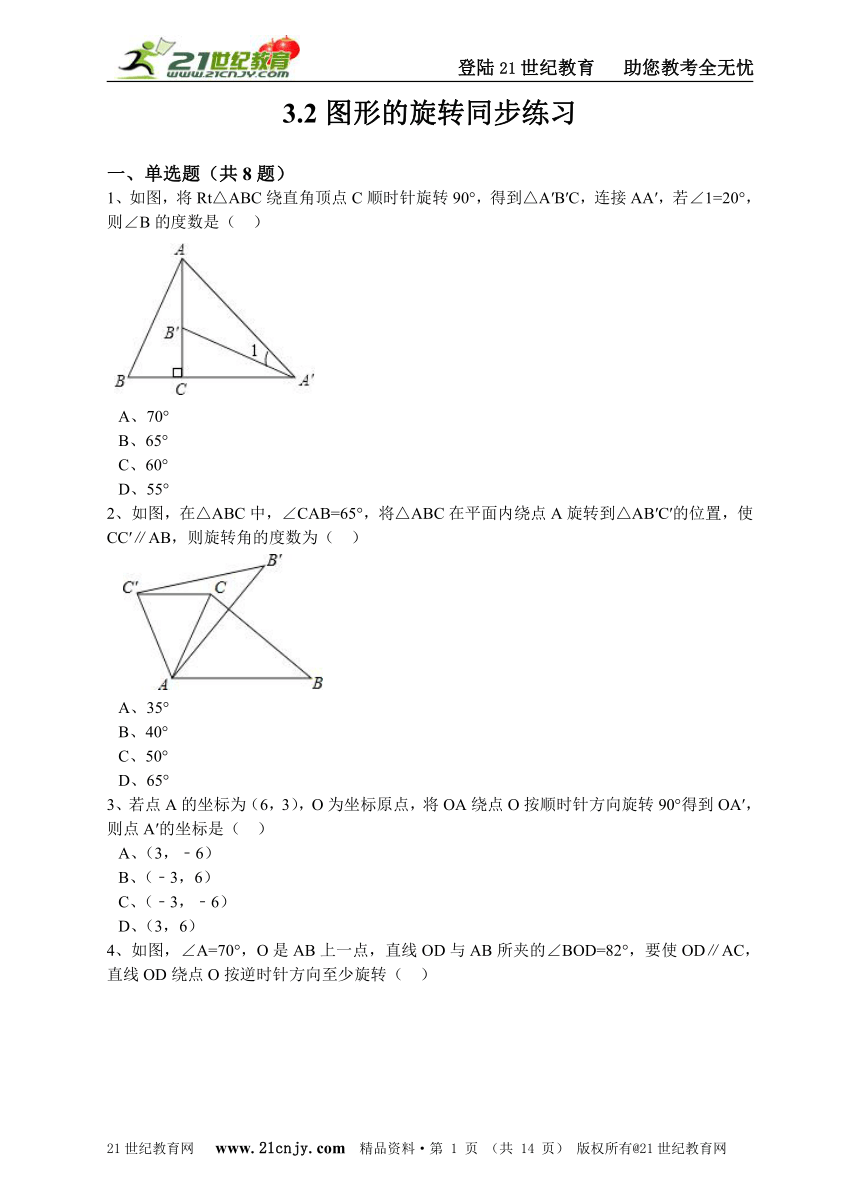
1、如图，将Rt△ABC绕直角顶点C顺时针旋转90°，得到△A′B′C，连接AA′，若∠1=20°，则∠B的度数是（?? ） www.21-cn-jy.com

A、70°B、65°C、60°D、55°
如图，在△ABC中，∠CAB=65°，将△ABC在平面内绕点A旋转到△AB′C′的位置，使CC′∥AB，则旋转角的度数为（?? ）【出处：21教育名师】

A、35°B、40°C、50°D、65°
3、若点A的坐标为（6，3），O为坐标原点，将OA绕点O按顺时针方向旋转90°得到OA′，则点A′的坐标是（?? ） 21教育网
A、（3，﹣6）B、（﹣3，6）C、（﹣3，﹣6）D、（3，6）
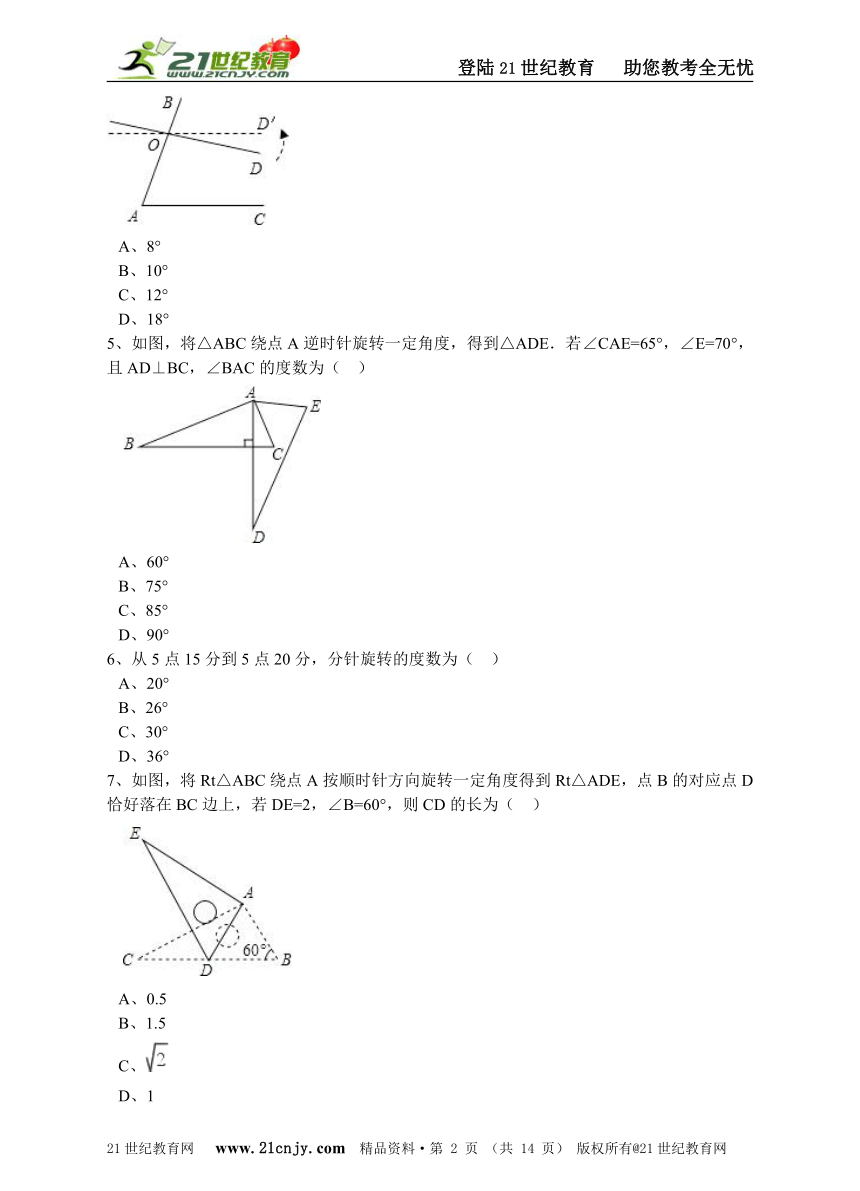
4、如图，∠A=70°，O是AB上一点，直线OD与AB所夹的∠BOD=82°，要使OD∥AC，直线OD绕点O按逆时针方向至少旋转（?? ） 【来源：21·世纪·教育·网】
A、8°B、10°C、12°D、18°
如图，将△ABC绕点A逆时针旋转一定角度，得到△ADE．若∠CAE=65°，∠E=70°，且AD⊥BC，∠BAC的度数为（?? ）www-2-1-cnjy-com

A、60°B、75°C、85°D、90°
6、从5点15分到5点20分，分针旋转的度数为（?? ）
A、20°B、26°C、30°D、36°
如图，将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若DE=2，∠B=60°，则CD的长为（?? ）21*cnjy*com

A、0.5B、1.5C、D、1
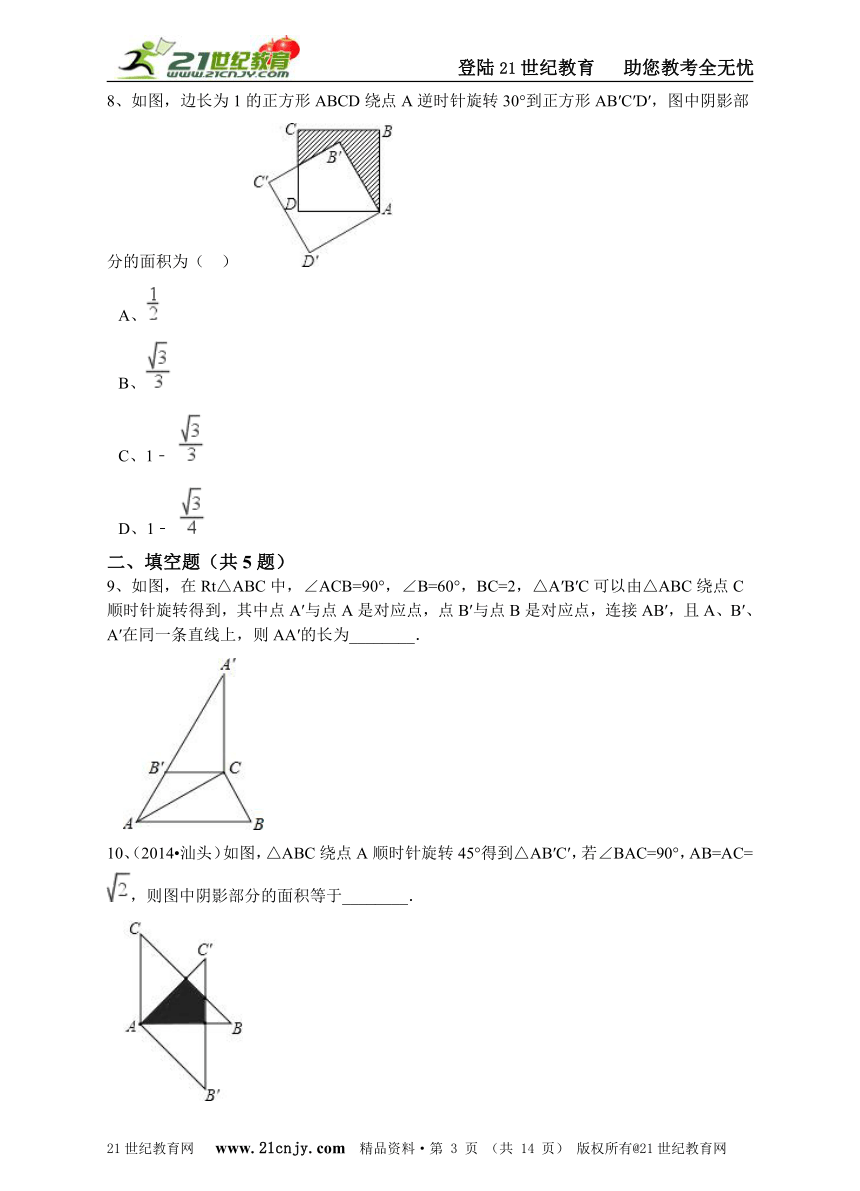
8、如图，边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′，图中阴影部分的面积为（?? ） 21*cnjy*com
A、B、C、1﹣ D、1﹣
二、填空题（共5题）
9、如图，在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2，△A′B′C可以由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，则AA′的长为________．

10、（2014?汕头）如图，△ABC绕点A顺时针旋转45°得到△AB′C′，若∠BAC=90°，AB=AC= ，则图中阴影部分的面积等于________．

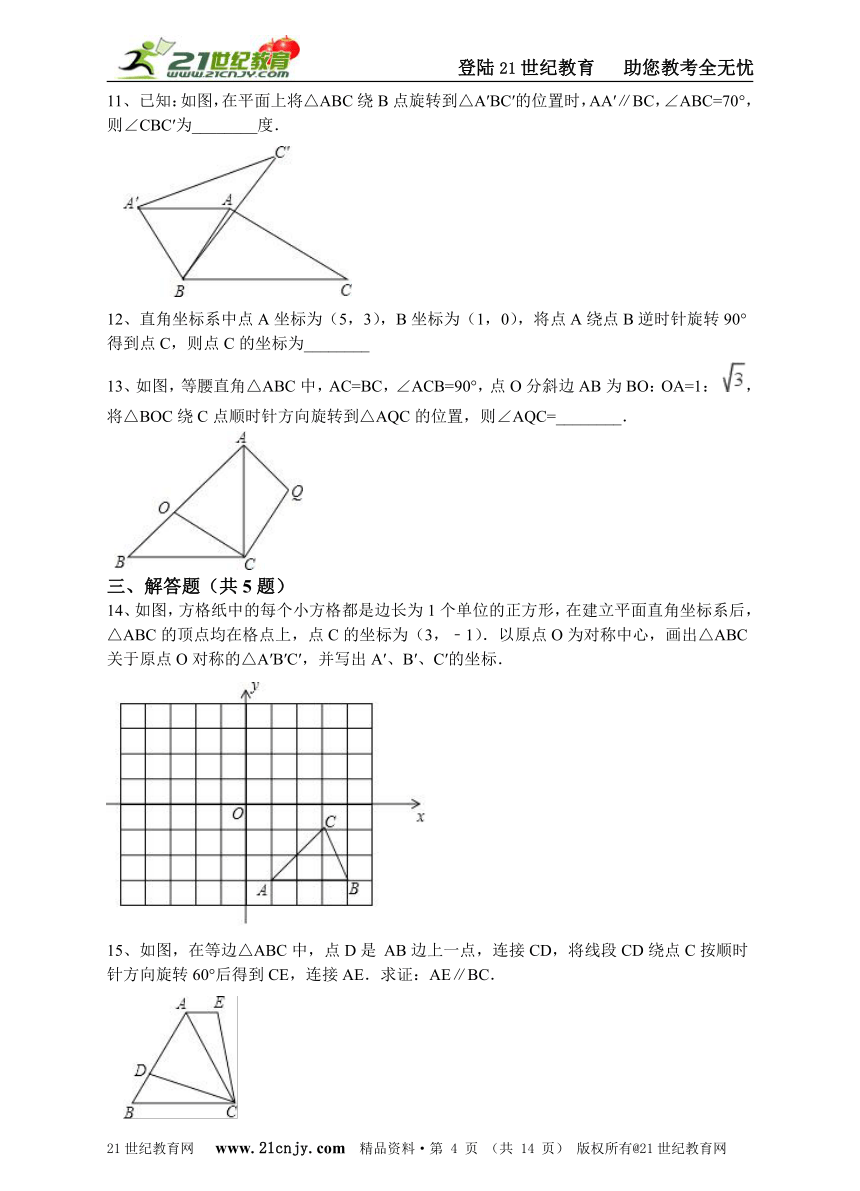
已知：如图，在平面上将△ABC绕B点旋转到△A′BC′的位置时，AA′∥BC，∠ABC=70°，则∠CBC′为________度．

12、直角坐标系中点A坐标为（5，3），B坐标为（1，0），将点A绕点B逆时针旋转90°得到点C，则点C的坐标为________
13、如图，等腰直角△ABC中，AC=BC，∠ACB=90°，点O分斜边AB为BO：OA=1： ，将△BOC绕C点顺时针方向旋转到△AQC的位置，则∠AQC=________．

三、解答题（共5题）
14、如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（3，﹣1）．以原点O为对称中心，画出△ABC关于原点O对称的△A′B′C′，并写出A′、B′、C′的坐标．
15、如图，在等边△ABC中，点D是 AB边上一点，连接CD，将线段CD绕点C按顺时针方向旋转60°后得到CE，连接AE．求证：AE∥BC．

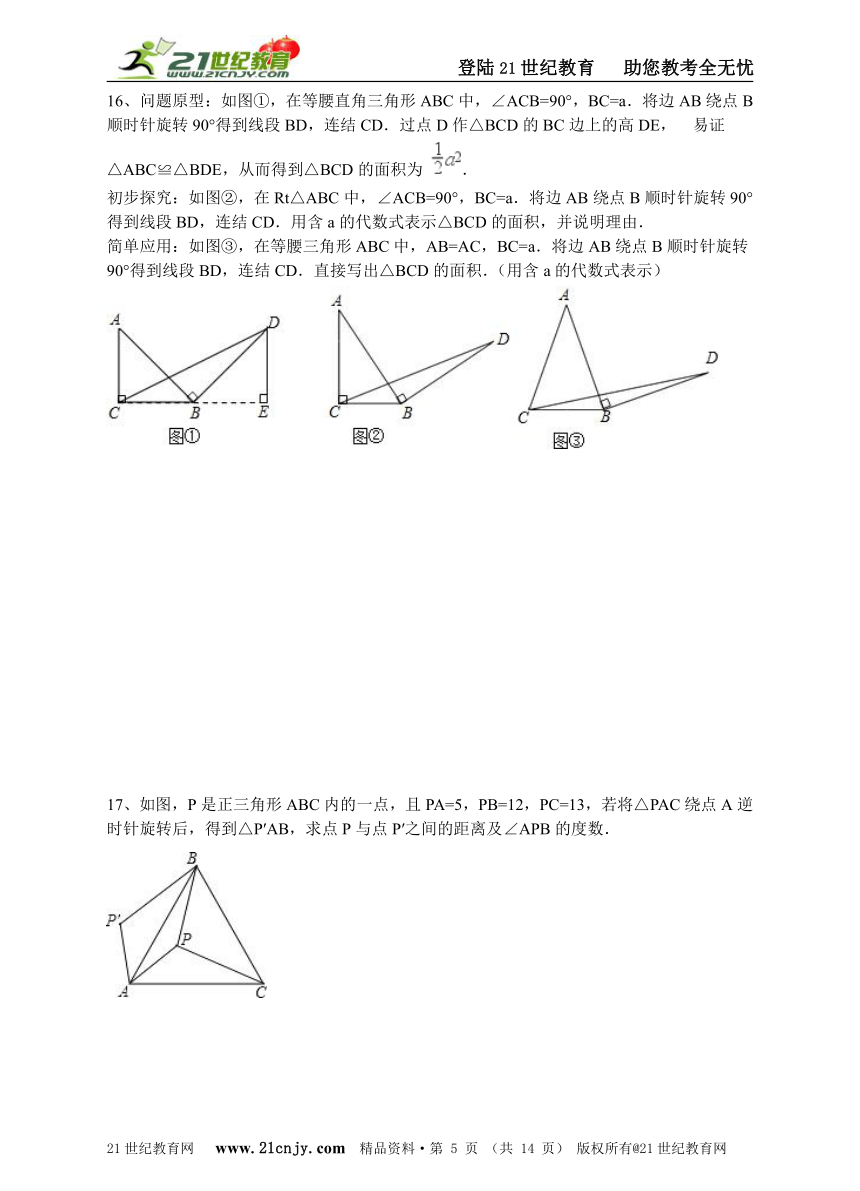
问题原型：如图①，在等腰直角三角形ABC中，∠ACB=90°，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．过点D作△BCD的BC边上的高DE， 易证△ABC≌△BDE，从而得到△BCD的面积为 ．初步探究：如图②，在Rt△ABC中，∠ACB=90°，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．用含a的代数式表示△BCD的面积，并说明理由．简单应用：如图③，在等腰三角形ABC中，AB=AC，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．直接写出△BCD的面积．（用含a的代数式表示）
17、如图，P是正三角形ABC内的一点，且PA=5，PB=12，PC=13，若将△PAC绕点A逆时针旋转后，得到△P′AB，求点P与点P′之间的距离及∠APB的度数． 21cnjy.com
18、如图，已知点D是等腰直角三角形ABC斜边BC上一点（不与点B重合），连AD，线段AD绕点A逆时针方向旋转90°得到线段AE，连CE，求证：BD⊥CE．


答案解析
一、单选题
1、B
2、C 解：∵CC′∥AB， ∴∠ACC′=∠CAB=65°，∵△ABC绕点A旋转得到△AB′C′，∴AC=AC′，∴∠CAC′=180°﹣2∠ACC′=180°﹣2×65°=50°，∴∠CAC′=∠BAB′=50°．21世纪教育网版权所有
故选C．3、A 解：由图知A点的坐标为（6，3），根据旋转中心O，旋转方向顺时针，旋转角度90°，画图，点A′的坐标是（3，﹣6）．故选：A． 4、C 解：∵AC∥OD′，∴∠BOD′=∠A=70°，∴∠DOD′=∠BOD﹣∠BOD′=82°﹣70°=12°，故选C． 21·cn·jy·com
5、C 解：根据旋转的性质知，∠EAC=∠BAD=65°，∠C=∠E=70°． 如图，设AD⊥BC于点F．则∠AFB=90°，∴在Rt△ABF中，∠B=90°﹣∠BAD=25°，∴在△ABC中，∠BAC=180°﹣∠B﹣∠C=180°﹣25°﹣70°=85°，即∠BAC的度数为85°．故选C． 2-1-c-n-j-y
6、C 解：∵分针旋转的速度为 =6（度/分钟）， ∴从5点15分到5点20分，分针旋转的度数为6×5=30（度），故选：C．21教育名师原创作品
7、D 解：由旋转得，DE=BC，AD=AB，∠B=∠ADE， ∴在Rt△ADE中，DE=2，∠ADE=60°，∴AB=1，BC=2，∵∠B=60°，∴BD=AB=1，∴CD=BC﹣BD=2﹣1=1，故选D．
8、C 解：如图，设B′C′与CD的交点为E，连接AE， 在Rt△AB′E和Rt△ADE中， ，∴Rt△AB′E≌Rt△ADE（HL），∴∠DAE=∠B′AE，∵旋转角为30°，∴∠DAB′=60°，∴∠DAE= ×60°=30°，∴DE=1× = ，∴阴影部分的面积=1×1﹣2×（ ×1× ）=1﹣ ．故选：C．
二、填空题
9、6 解：∵在Rt△ABC中，∠ACB=90°，∠B=60°，BC=2， ∴∠CAB=30°，故AB=4，∵△A′B′C由△ABC绕点C顺时针旋转得到，其中点A′与点A是对应点，点B′与点B是对应点，连接AB′，且A、B′、A′在同一条直线上，∴AB=A′B′=4，AC=A′C，∴∠CAA′=∠A′=30°，∴∠ACB′=∠B′AC=30°，∴AB′=B′C=2，∴AA′=2+4=6，故答案为6． 【版权所有：21教育】
10、﹣1 解：∵△ABC绕点A顺时针旋转45°得到△AB′C′，∠BAC=90°，AB=AC= ， ∴BC=2，∠C=∠B=∠CAC′=∠C′=45°，∴AD⊥BC，B′C′⊥AB，∴AD= BC=1，AF=FC′=sin45°AC′= AC′=1，∴图中阴影部分的面积等于：S△AFC′﹣S△DEC′= ×1×1﹣ ×（ ﹣1）2= ﹣1．故答案为： ﹣1．
11、40 解：∵AA′∥BC， ∴∠A′AB=∠ABC=70°．∵BA′=AB，∴∠BA′A=∠BAA′=70°，∴∠ABA′=40°，又∵∠A′BA+∠ABC'=∠CBC'+∠ABC'，∴∠CBC′=∠ABA′，即可得出∠CBC'=40°．故答案为：40°．21·世纪*教育网
（﹣2，4） 解：如图所示，点A绕点B逆时针旋转90°到点C， ∵A坐标为（5，3），B坐标为（1，0），∴AD=3，BD=4，∴AB=5，根据旋转的性质，AB=BC，∵∠ABC=90°，∴∠EBC+∠ABD=90°，∵∠DAB+∠ABD=90°，∴∠EBC=∠DAB．在△EBC和△BAD中，∴△EBC≌△BAD，∴CE=BD=4，BE=AD=3，∵OB=1，∴OE=2，∴C（﹣2，4）．故答案为：（﹣2，4）．
13、105° 解：连接OQ， ∵AC=BC，∠ACB=90°，∴∠BAC=∠B=45°，由旋转的性质可知：△AQC≌△BOC，∴AQ=BO，CQ=CO，∠QAC=∠B=45°，∠ACQ=∠BCO，∴∠OAQ=∠BAC+∠CAQ=90°，∠OCQ=∠OCA+∠ACQ=∠OCA+∠BCO=90°，∴∠OQC=45°，∵BO：OA=1： ，设BO=1，OA= ，∴AQ=1，则tan∠AQO= = ，∴∠AQO=60°，∴∠AQC=105°．
三、解答题
14、解：如图所示，△A′B′C′即为所求三角形： 其中A'（﹣1，3），B'（﹣4，3），C'（﹣3，1） 2·1·c·n·j·y
15、解：∵△ABC是等边三角形， ∴AC=BC，∠B=∠ACB=60°．∵线段CD绕点C顺时针旋转60°得到CE，∴CD=CE，∠DCE=60°，∴∠DCE=∠ACB，即∠BCD+∠DCA=∠DCA+∠ACE，∴∠BCD=∠ACE，在△BCD与△ACE中， ∴△BCD≌△ACE，∴∠EAC=∠B=60°，∴∠EAC=∠ACB，∴AE∥BC．
16、解：初步探究：△BCD的面积为 ． 理由：如图②，过点D作BC的垂线，与BC的延长线交于点E． ∴∠BED=∠ACB=90°．∵线段AB绕点B顺时针旋转90°得到线段BE，∴AB=BD，∠ABD=90°．∴∠ABC+∠DBE=90°．∵∠A+∠ABC=90°．∴∠A=∠DBE．在△ABC和△BDE中，，∴△ABC≌△BDE（AAS）∴BC=DE=a．∵S△BCD= BC?DE∴S△BCD= ；简单应用：如图③，过点A作AF⊥BC与F，过点D作DE⊥BC的延长线于点E， ∴∠AFB=∠E=90°，BF= BC= a．∴∠FAB+∠ABF=90°．∵∠ABD=90°，∴∠ABF+∠DBE=90°，∴∠FAB=∠EBD．∵线段BD是由线段AB旋转得到的，∴AB=BD．在△AFB和△BED中，，∴△AFB≌△BED（AAS），∴BF=DE= a．∵S△BCD= BC?DE，∴S△BCD= ? a?a= a2 ． ∴△BCD的面积为 ． 【来源：21cnj*y.co*m】

18、证明：∵△ABC为等腰直角三角形， ∴∠B=∠ACB=45°，∵线段AD绕点A逆时针方向旋转90°得到线段AE，∴∠ACE=∠B=45°，∴∠ACB+∠ACE=45°+45°=90°，即∠BCE=90°，∴BD⊥CE．