山东省龙口五中(五四学制)2016-2017学年九年级下学期期中考试数学试卷
文档属性
| 名称 | 山东省龙口五中(五四学制)2016-2017学年九年级下学期期中考试数学试卷 |  | |
| 格式 | zip | ||
| 文件大小 | 388.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-08 17:56:27 | ||
图片预览




文档简介
2016—2017学年第二学期期中考试
初四数学
说明:1.本卷共有三个大题,25个小题,全卷满分120分,考试时间120分钟.
2.本卷分为试题卷和答题卷,答案要求写在答题卷上,在试题卷上作答,不得分.
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1.有下列四个论断:-是有理数;是分数;1.232232223···是无理数;π是无理数,其中正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
2.据报道,目前我国“天河二号”超级计算机
( http: / / www.21cnjy.com )的运算速度位居全球第一,其运算速度达到了每秒338
600
000亿次,数字338
600
000用科学记数法(保留3个有效数字)可简洁表示为(
)
A.3.4×108
B.0.34×109
C.3.38×108
D.3.39×108
3.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
4.下列运算正确的是( )
A.x2+x3=x5
B.a3 a2=a6
C.(﹣x3)2÷x5=1
D.(﹣xy)3 (﹣xy)﹣2=﹣xy
5.一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是( )
( http: / / www.21cnjy.com )
A.2
B.3
C.4
D.5
6.
下列说法正确的个数是( )
①一组数据的众数只有一个;
②样
( http: / / www.21cnjy.com )本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④数据:1,1,3,1,1,2的众数为4; ⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
7.如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(
)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
8.平面直角坐标系中,已知、、三点,是一个动点,当周长最小时,的面积为
B.
C.
D.
9.若分式不论x取何值总有意义,则m的取值范围是(
)
A.m≥1
B.m≤1
C.m>1
D.m<1
10.
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为(
)
A.π
B.π
C.π
D.π
11.如图,已知抛物线y=
( http: / / www.21cnjy.com )ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论①abc>0;②a﹣b+c<0;
③阴影部分的面积为4;
④若c=﹣1,则b2=4a.中正确的有(
)
A.1个 B.2个 C.3个 D.4个
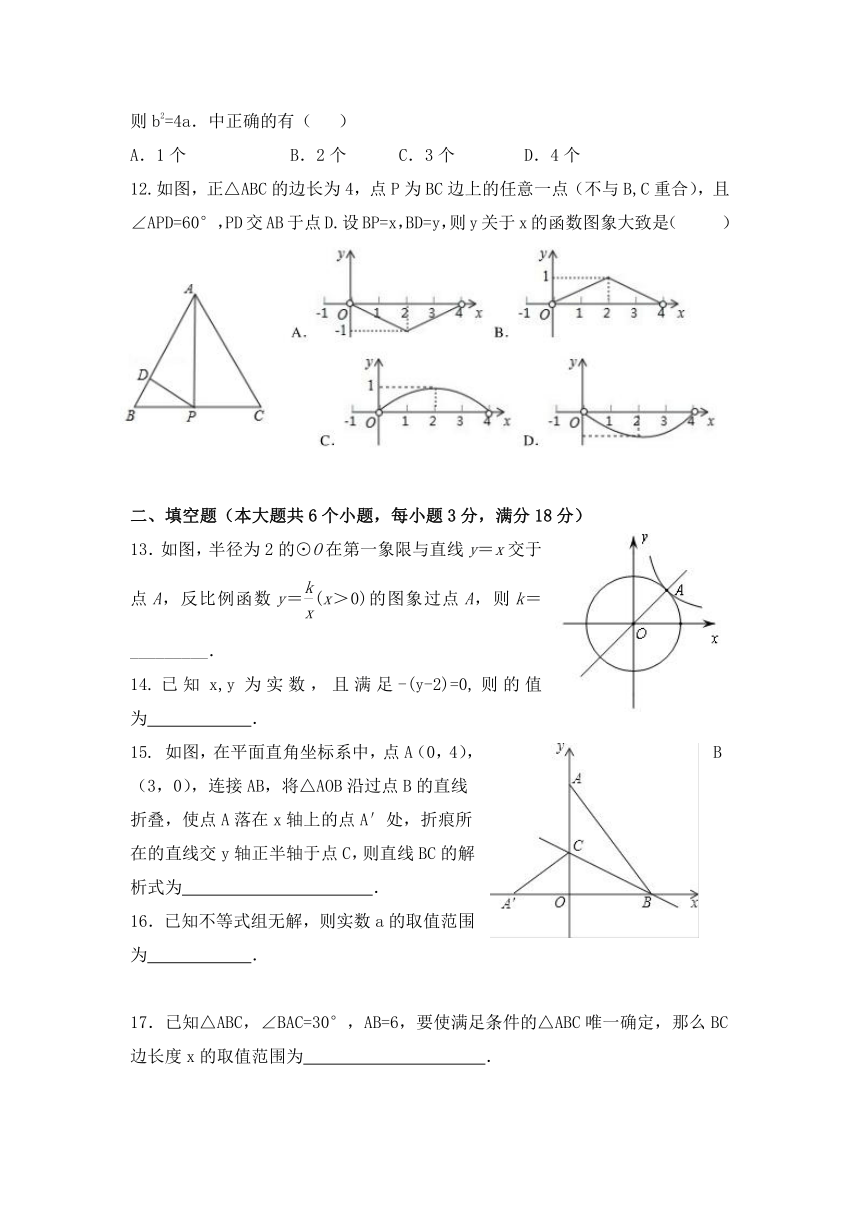
12.如图,正△ABC的边长为4,点P为BC边上的任意一点(不与B,C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是(
)
( http: / / www.21cnjy.com )
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.如图,半径为2的⊙O在第一象限与直线y=x交于点A,反比例函数y=(x>0)的图象过点A,则k=_________.
14.已知x,y为实数,且满足-(y-2)=0,则的值为 .
15.
如图,在平面直角坐标系中,点A
( http: / / www.21cnjy.com )(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为
.
16.已知不等式组无解,则实数a的取值范围为 .
17.已知△ABC,∠BAC=30
( http: / / www.21cnjy.com )°,AB=6,要使满足条件的△ABC唯一确定,那么BC边长度x的取值范围为
.
18.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点(0,1),(1,1),(1,0),(1,-1),(2,-1),(2,0),…,则点的坐标是
.
三、解答题(本大题共7小题,满分66分)
19.(本题满分6分)先化简,再求值:(+)÷,其中a与2,3构成△ABC的三边,且a为整数.
20.
(本题满分8分)
某校要求
( http: / / www.21cnjy.com )八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位
( http: / / www.21cnjy.com )男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
21.
(本题满分9分)如
( http: / / www.21cnjy.com )图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,
铅笔芯端点B可以绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18 时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18 不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,
求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9 ≈0.1564,com9 ≈0.9877 ,
sin18 ≈0.3090,
com18 ≈0.9511)
22.
(本题满分9分)
( http: / / www.21cnjy.com )
旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
23.
(本题满分11分)
如图,AB
( http: / / www.21cnjy.com )是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=,E是的中点,求EG ED的值.
( http: / / www.21cnjy.com )
24.(本题满分9分)在平面直角坐标系xOy中,抛物线(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
( http: / / www.21cnjy.com )
25.(本题满分14分)已知:如图,在
( http: / / www.21cnjy.com )矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
( http: / / www.21cnjy.com )
2016—2017学年第二学期期中考试
初四数学答题卷
一、选择题(本题共12个小题,每小题3分,满分36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.
;
15.
;17.
;14.
;
16.
;18.
.
三、解答题(本大题共7小题,满分66分)
19.
20.
21.(1)(2)
22.
23.
24.
25.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
备用图1
备用图2
备用图3
2016—2017学年第二学期期中考试
初四数学答案
选择题(本题共12个小题,每小题3分,满分36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
D
C
B
C
C
C
A
C
C
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.
2
;14.
;15.
y=﹣x+ ;16.a≤-1
;
17.x=3或x≥6;
18.
(20,0)
三、解答题(本大题共7小题,满分66分)
19.(本题满分6分)
原式=
··········3分
原式=1
··········6分
20.
(本题满分8分)
解:(1)a=5÷12.5%×40%=16,5÷12.5%=7÷b%,
∴b=17.5,
故答案为:16,17.5;··············2分
(2)600×[6÷(5÷12.5%)]=90(人),
故答案为:90;·················4分
(3)如图,∵共有20种等可能的结果,两名主持人恰为一男一女的有12种情况,
∴则P(恰好选到一男一女)==.
HYPERLINK
"http://www.21cnjy.com"
·········8分
21.
(本题满分9分)(1)
图1,作OC⊥AB,
∵OA=OB,
OC⊥AB,∴AC=BC,
∠AOC=∠BOC=∠AOB=9°,
在Rt△AOC
中,sin∠AOC
=
,
∴AC≈0.1564×10=1.564,
∴AB=2AC=3.128≈3.13.
∴所作圆的半径是3.13cm.
············4分
(2)图2,以点A为圆心,AB长为半径画弧,交OB于点C,
作AD⊥BC于点D;
∵AC=AB,
AD⊥BC,
∴BD=CD,
∠BAD=∠CAD=∠BAC,
∵∠AOB=18°,OA=OB
,AB=AC,
∴∠BAC=18°,
∴∠BAD=9°,
在Rt△BAD
中,
sin∠BAD
=
,
∴BD≈0.1564×3.128≈0.4892,
∴BC=2BD=0.9784≈0.98
∴铅笔芯折断部分的长度约为0.98cm.
··············9分
22.
(本题满分9分)
解:(1)由题意知,若观光车能全部租出,则0<x≤100,
由50x﹣1100>0,
解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元;················3分
(2)设每天的净收入为y元,
当0<x≤100时,y1=50x﹣1100,
∵y1随x的增大而增大,
∴当x=100时,y1的最大值为50×100﹣1100=3900;
当x>100时,
y2=(50﹣)x﹣1100
=﹣x2+70x﹣1100
=﹣(x﹣175)2+5025,
当x=175时,y2的最大值为5025,
5025>3900,
故当每辆车的日租金为175元时,每天的净收入最多是5025元.·······9分
23.
(本题满分11分)
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;············3分
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°﹣∠E,
又∵∠CFD=180°﹣∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;···········5分
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB=,BD=4,
∴AB=6,
∵E是的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3,
∵E是的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴=,
即EG ED=AE2=18.···············11分
24.
(本题满分9分)
解析:(1)将抛物线表达式变为顶点式,则抛物线顶点坐标为(1,-1);·············2分
(2)①m=1时,抛物线表达式为,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;··4分
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;又有抛物线表达式,令y=0,则,得到A、B两点坐标分别为(,0),(,0),即5个整点是以(1,0)为中心向两侧分散,进而得到,∴.·············9分
( http: / / www.21cnjy.com )
25.
(本题满分14分)
解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,
∴AC=10,
①当AP=PO=t,如图1,过P作PM⊥AO,
∴AM=AO=,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ADC,
∴,
∴AP=t=,
②当AP=AO=t=5,
∴当t为或5时,△AOP是等腰三角形;···········3分
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,
在△APO与△CEO中,
,
∴△AOP≌△COE,
∴CE=AP=t,
∵△CEH∽△ABC,
∴,
∴EH=,
∵DN==,
∵QM∥DN,
∴△CQM∽△CDN,
∴,即,
∴QM=,
∴DG=﹣=,
∵FQ∥AC,
∴△DFQ∽△DOC,
∴,
∴FQ=,
∴S五边形OECQF=S△OEC+S四边形OCQF=×5×+(+5) =﹣t2+t+12,
∴S与t的函数关系式为S=﹣t2+t+12;···········8分
(3)存在,
∵S△ACD=×6×8=24,
∴S五边形OECQF:S△ACD=(﹣t2+t+12):24=9:16,
解得t=,t=0,(不合题意,舍去),
∴t=时,
S五边形OECQF:S△ACD=9:16;
(4)如图3,过D作DM⊥PE于M,DN⊥AC于N,
∵∠POD=∠COD,
∴DM=DN=,
∴ON=OM==,
∵OP DM=3PD,
∴OP=5﹣t,
∴PM=﹣t,
∵PD2=PM2+DM2,
∴(8﹣t)2=(﹣t)2+()2,
解得:t=16(不合题意,舍去),t=
,
∴当t=
时,OD平分∠COP.················14分
初四数学
说明:1.本卷共有三个大题,25个小题,全卷满分120分,考试时间120分钟.
2.本卷分为试题卷和答题卷,答案要求写在答题卷上,在试题卷上作答,不得分.
一、选择题(本题共12个小题,每小题3分,满分36分)每小题都给出标号为A,B,C,D四个备选答案,其中有且只有一个是正确的.
1.有下列四个论断:-是有理数;是分数;1.232232223···是无理数;π是无理数,其中正确的个数是(
)
A.1个
B.2个
C.3个
D.4个
2.据报道,目前我国“天河二号”超级计算机
( http: / / www.21cnjy.com )的运算速度位居全球第一,其运算速度达到了每秒338
600
000亿次,数字338
600
000用科学记数法(保留3个有效数字)可简洁表示为(
)
A.3.4×108
B.0.34×109
C.3.38×108
D.3.39×108
3.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
4.下列运算正确的是( )
A.x2+x3=x5
B.a3 a2=a6
C.(﹣x3)2÷x5=1
D.(﹣xy)3 (﹣xy)﹣2=﹣xy
5.一个几何体由几个大小相同的小正方体搭成,其左视图和俯视图如图所示,则搭成这个几何体的小正方体的个数是( )
( http: / / www.21cnjy.com )
A.2
B.3
C.4
D.5
6.
下列说法正确的个数是( )
①一组数据的众数只有一个;
②样
( http: / / www.21cnjy.com )本的方差越小,波动性越小,说明样本稳定性越好;③一组数据的中位数一定是这组数据中的某一数据;④数据:1,1,3,1,1,2的众数为4; ⑤一组数据的方差一定是正数.
A.0个 B.1个 C.2个 D.4个
7.如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(
)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
8.平面直角坐标系中,已知、、三点,是一个动点,当周长最小时,的面积为
B.
C.
D.
9.若分式不论x取何值总有意义,则m的取值范围是(
)
A.m≥1
B.m≤1
C.m>1
D.m<1
10.
如图,方格纸中4个小正方形的边长均为1,则图中阴影部分三个小扇形的面积和为(
)
A.π
B.π
C.π
D.π
11.如图,已知抛物线y=
( http: / / www.21cnjy.com )ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为﹣2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论①abc>0;②a﹣b+c<0;
③阴影部分的面积为4;
④若c=﹣1,则b2=4a.中正确的有(
)
A.1个 B.2个 C.3个 D.4个
12.如图,正△ABC的边长为4,点P为BC边上的任意一点(不与B,C重合),且∠APD=60°,PD交AB于点D.设BP=x,BD=y,则y关于x的函数图象大致是(
)
( http: / / www.21cnjy.com )
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.如图,半径为2的⊙O在第一象限与直线y=x交于点A,反比例函数y=(x>0)的图象过点A,则k=_________.
14.已知x,y为实数,且满足-(y-2)=0,则的值为 .
15.
如图,在平面直角坐标系中,点A
( http: / / www.21cnjy.com )(0,4),B(3,0),连接AB,将△AOB沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为
.
16.已知不等式组无解,则实数a的取值范围为 .
17.已知△ABC,∠BAC=30
( http: / / www.21cnjy.com )°,AB=6,要使满足条件的△ABC唯一确定,那么BC边长度x的取值范围为
.
18.如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点(0,1),(1,1),(1,0),(1,-1),(2,-1),(2,0),…,则点的坐标是
.
三、解答题(本大题共7小题,满分66分)
19.(本题满分6分)先化简,再求值:(+)÷,其中a与2,3构成△ABC的三边,且a为整数.
20.
(本题满分8分)
某校要求
( http: / / www.21cnjy.com )八年级同学在课外活动中,必须在五项球类(篮球、足球、排球、羽毛球、乒乓球)活动中任选一项(只能选一项)参加训练,为了了解八年级学生参加球类活动的整体情况,现以八年级2班作为样本,对该班学生参加球类活动的情况进行统计,并绘制了如图所示的不完整统计表和扇形统计图:
八年级2班参加球类活动人数统计表
项目
篮球
足球
乒乓球
排球
羽毛球
人数
a
6
5
7
6
根据图中提供的信息,解答下列问题:
(1)a= ,b= ;
(2)该校八年级学生共有600人,则该年级参加足球活动的人数约 人;
(3)该班参加乒乓球活动的5位同学中,有3位
( http: / / www.21cnjy.com )男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
21.
(本题满分9分)如
( http: / / www.21cnjy.com )图1是一副创意卡通圆规,图2是其平面示意图,OA是支撑臂,OB是旋转臂,使用时,以点A为支撑点,
铅笔芯端点B可以绕点A旋转作出圆.已知OA=OB=10cm.
(1)当∠AOB=18 时,求所作圆的半径;(结果精确到0.01cm)
(2)保持∠AOB=18 不变,在旋转臂OB末端的铅笔芯折断了一截的情况下,作出的圆与(1)中所作圆的大小相等,
求铅笔芯折断部分的长度.(结果精确到0.01cm)
(参考数据:sin9 ≈0.1564,com9 ≈0.9877 ,
sin18 ≈0.3090,
com18 ≈0.9511)
22.
(本题满分9分)
( http: / / www.21cnjy.com )
旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
23.
(本题满分11分)
如图,AB
( http: / / www.21cnjy.com )是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.
(1)证明:∠E=∠C;
(2)若∠E=55°,求∠BDF的度数;
(3)设DE交AB于点G,若DF=4,cosB=,E是的中点,求EG ED的值.
( http: / / www.21cnjy.com )
24.(本题满分9分)在平面直角坐标系xOy中,抛物线(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
( http: / / www.21cnjy.com )
25.(本题满分14分)已知:如图,在
( http: / / www.21cnjy.com )矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点0.点P从点A出发,沿方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6),解答下列问题:
(1)当t为何值时,△AOP是等腰三角形?
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使S五边形OECQF:S△ACD=9:16?若存在,求出t的值;若不存在,请说明理由;
(4)在运动过程中,是否存在某一时刻t,使OD平分∠COP?若存在,求出t的值;若不存在,请说明理由.
( http: / / www.21cnjy.com )
2016—2017学年第二学期期中考试
初四数学答题卷
一、选择题(本题共12个小题,每小题3分,满分36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.
;
15.
;17.
;14.
;
16.
;18.
.
三、解答题(本大题共7小题,满分66分)
19.
20.
21.(1)(2)
22.
23.
24.
25.
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
备用图1
备用图2
备用图3
2016—2017学年第二学期期中考试
初四数学答案
选择题(本题共12个小题,每小题3分,满分36分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
D
B
D
C
B
C
C
C
A
C
C
二、填空题(本大题共6个小题,每小题3分,满分18分)
13.
2
;14.
;15.
y=﹣x+ ;16.a≤-1
;
17.x=3或x≥6;
18.
(20,0)
三、解答题(本大题共7小题,满分66分)
19.(本题满分6分)
原式=
··········3分
原式=1
··········6分
20.
(本题满分8分)
解:(1)a=5÷12.5%×40%=16,5÷12.5%=7÷b%,
∴b=17.5,
故答案为:16,17.5;··············2分
(2)600×[6÷(5÷12.5%)]=90(人),
故答案为:90;·················4分
(3)如图,∵共有20种等可能的结果,两名主持人恰为一男一女的有12种情况,
∴则P(恰好选到一男一女)==.
HYPERLINK
"http://www.21cnjy.com"
·········8分
21.
(本题满分9分)(1)
图1,作OC⊥AB,
∵OA=OB,
OC⊥AB,∴AC=BC,
∠AOC=∠BOC=∠AOB=9°,
在Rt△AOC
中,sin∠AOC
=
,
∴AC≈0.1564×10=1.564,
∴AB=2AC=3.128≈3.13.
∴所作圆的半径是3.13cm.
············4分
(2)图2,以点A为圆心,AB长为半径画弧,交OB于点C,
作AD⊥BC于点D;
∵AC=AB,
AD⊥BC,
∴BD=CD,
∠BAD=∠CAD=∠BAC,
∵∠AOB=18°,OA=OB
,AB=AC,
∴∠BAC=18°,
∴∠BAD=9°,
在Rt△BAD
中,
sin∠BAD
=
,
∴BD≈0.1564×3.128≈0.4892,
∴BC=2BD=0.9784≈0.98
∴铅笔芯折断部分的长度约为0.98cm.
··············9分
22.
(本题满分9分)
解:(1)由题意知,若观光车能全部租出,则0<x≤100,
由50x﹣1100>0,
解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元;················3分
(2)设每天的净收入为y元,
当0<x≤100时,y1=50x﹣1100,
∵y1随x的增大而增大,
∴当x=100时,y1的最大值为50×100﹣1100=3900;
当x>100时,
y2=(50﹣)x﹣1100
=﹣x2+70x﹣1100
=﹣(x﹣175)2+5025,
当x=175时,y2的最大值为5025,
5025>3900,
故当每辆车的日租金为175元时,每天的净收入最多是5025元.·······9分
23.
(本题满分11分)
(1)证明:连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,即AD⊥BC,
∵CD=BD,
∴AD垂直平分BC,
∴AB=AC,
∴∠B=∠C,
又∵∠B=∠E,
∴∠E=∠C;············3分
(2)解:∵四边形AEDF是⊙O的内接四边形,
∴∠AFD=180°﹣∠E,
又∵∠CFD=180°﹣∠AFD,
∴∠CFD=∠E=55°,
又∵∠E=∠C=55°,
∴∠BDF=∠C+∠CFD=110°;···········5分
(3)解:连接OE,
∵∠CFD=∠E=∠C,
∴FD=CD=BD=4,
在Rt△ABD中,cosB=,BD=4,
∴AB=6,
∵E是的中点,AB是⊙O的直径,
∴∠AOE=90°,
∵AO=OE=3,
∴AE=3,
∵E是的中点,
∴∠ADE=∠EAB,
∴△AEG∽△DEA,
∴=,
即EG ED=AE2=18.···············11分
24.
(本题满分9分)
解析:(1)将抛物线表达式变为顶点式,则抛物线顶点坐标为(1,-1);·············2分
(2)①m=1时,抛物线表达式为,因此A、B的坐标分别为(0,0)和(2,0),则线段AB上的整点有(0,0),(1,0),(2,0)共3个;··4分
②抛物线顶点为(1,-1),则由线段AB之间的部分及线段AB所围成的区域的整点的纵坐标只能为-1或者0,所以即要求AB线段上(含AB两点)必须有5个整点;又有抛物线表达式,令y=0,则,得到A、B两点坐标分别为(,0),(,0),即5个整点是以(1,0)为中心向两侧分散,进而得到,∴.·············9分
( http: / / www.21cnjy.com )
25.
(本题满分14分)
解:(1)∵在矩形ABCD中,AB=6cm,BC=8cm,
∴AC=10,
①当AP=PO=t,如图1,过P作PM⊥AO,
∴AM=AO=,
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ADC,
∴,
∴AP=t=,
②当AP=AO=t=5,
∴当t为或5时,△AOP是等腰三角形;···········3分
(2)作EH⊥AC于H,QM⊥AC于M,DN⊥AC于N,交QF于G,
在△APO与△CEO中,
,
∴△AOP≌△COE,
∴CE=AP=t,
∵△CEH∽△ABC,
∴,
∴EH=,
∵DN==,
∵QM∥DN,
∴△CQM∽△CDN,
∴,即,
∴QM=,
∴DG=﹣=,
∵FQ∥AC,
∴△DFQ∽△DOC,
∴,
∴FQ=,
∴S五边形OECQF=S△OEC+S四边形OCQF=×5×+(+5) =﹣t2+t+12,
∴S与t的函数关系式为S=﹣t2+t+12;···········8分
(3)存在,
∵S△ACD=×6×8=24,
∴S五边形OECQF:S△ACD=(﹣t2+t+12):24=9:16,
解得t=,t=0,(不合题意,舍去),
∴t=时,
S五边形OECQF:S△ACD=9:16;
(4)如图3,过D作DM⊥PE于M,DN⊥AC于N,
∵∠POD=∠COD,
∴DM=DN=,
∴ON=OM==,
∵OP DM=3PD,
∴OP=5﹣t,
∴PM=﹣t,
∵PD2=PM2+DM2,
∴(8﹣t)2=(﹣t)2+()2,
解得:t=16(不合题意,舍去),t=
,
∴当t=
时,OD平分∠COP.················14分
同课章节目录
