5.2 探索轴对称的性质 学案(含答案)
文档属性
| 名称 | 5.2 探索轴对称的性质 学案(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 907.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-12 00:00:00 | ||
图片预览

文档简介
5.2
探索轴对称的性质
【学习目标】
理解对应点所连的线段被对称轴垂直平分.
对应线段相等、对应角相等的性质.
【重点难点】
重点:理解“对应点所连的线段被对称轴垂直平分、对应线段相等、对应角相等”的性质.
难点:运用对称轴的性质
【学习过程】
情境导入
如下图所示,方格内的图形都是轴对称的,请画出它们的对称轴.
自主学习
一、掌握轴对称的性质
1.轴对称的性质
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等.
2.轴对称图形的性质
(1)轴对称图形对应点所连的线段被对称轴垂直平分;
(2)轴对称图形对应线段相等,对应角相等.
导学解疑:
一、展示点拨,归纳新知:
二、典例分析
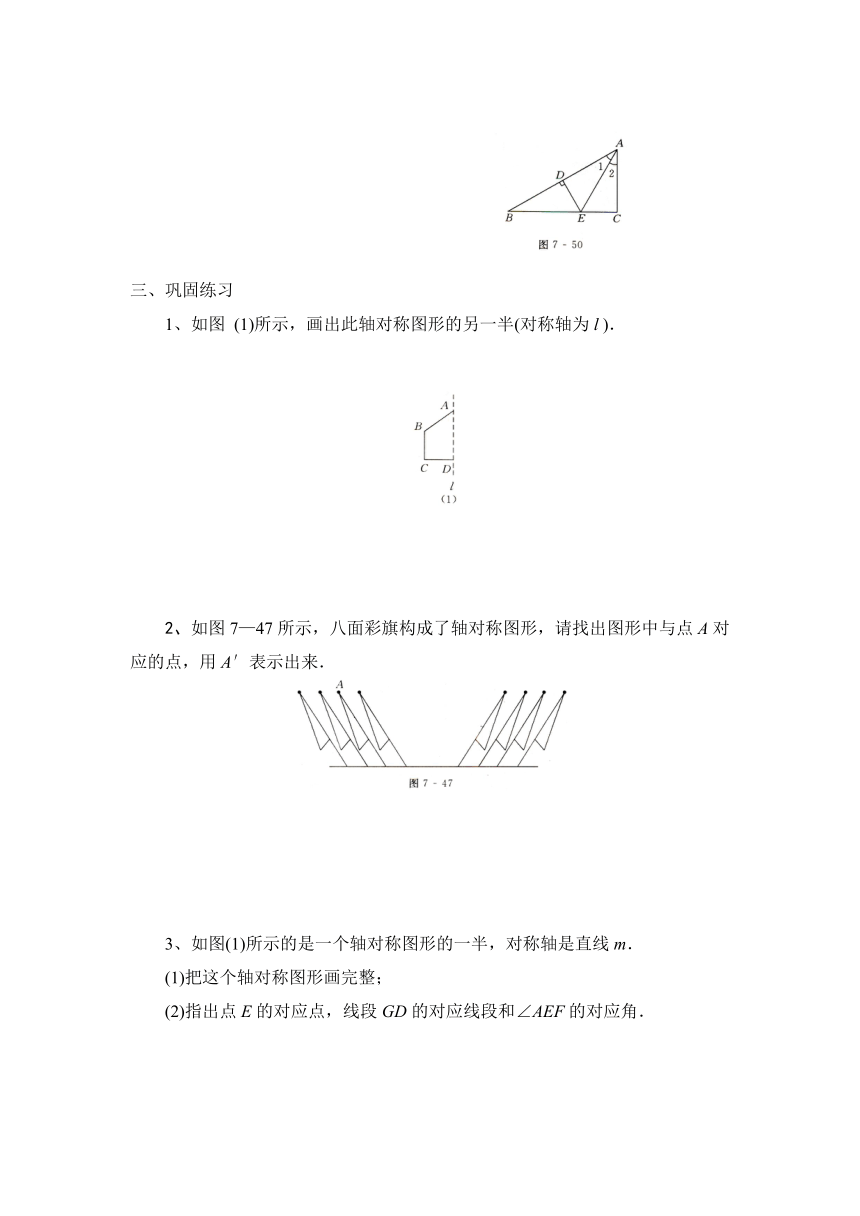
1、如图7—50所示,DE是ΔABC的AB边的垂直平分线,分别交AB,BC于D,E,AE平分∠BAC,若∠B=30°,求∠C的度数.
三、巩固练习
1、如图
(1)所示,画出此轴对称图形的另一半(对称轴为l
).
2、如图7—47所示,八面彩旗构成了轴对称图形,请找出图形中与点A对
应的点,用A′表示出来.
3、如图(1)所示的是一个轴对称图形的一半,对称轴是直线m.
(1)把这个轴对称图形画完整;
(2)指出点E的对应点,线段GD的对应线段和∠AEF的对应角.
成果检验
一、达标测评
1、如图7—52所示的矩形纸片,先沿虚线按箭头方向向右对折,接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形,然后将纸片打开,得到的图形是图7—53中的
(
)
二、总结延伸:
1.
本节课的收获:先由学生总结,老师启发补充
2.
本节课渗透的数学思想方法
3.
关于这一课的知识你还有不明白的地方吗?如果有请提出来,让老师和同学帮你解决。
答案
典例分析
1、【分析】由DE是AB边的垂直平分线,可知DE是ΔABE的对称轴,故对应角∠1=∠B。而AE是∠BAC的平分线,所以∠1=∠2.再由三角形内角和定理可求得∠C的度数.
解:因为DE是AB的垂直平分线,所以EA=EB,所以∠l=∠B.
又因为∠B=30°,所以∠1=30°.
因为AE平分∠BAC,所以∠2=∠1=30°,即∠BAC=60°.
所以∠C=180°-∠B-∠BAC=180°-30°-60°=90°.
【解题策略】
灵活运用线段垂直平分线、角平分线、三角形内角和的性质解决问题.
巩固练习
1、解:如图7—46(2)所示,过B点作l的垂线,取OB′=OB,B′是B点的对应点,同理找出C点的对应点C′,点A和D的对应点还是它本身,连接A′,B′,C′,D′,得到轴对称图形关于对称轴对称的另一半.
【解题策略】
解此题的关键是根据轴对称图形的性质画出关键点A,B,C,D关于直线l的对称点.
2、【分析】可以画出这个图形的对称轴,利用轴对称图形的性质进行判断.也可先
凭观察得出初步结论,然后进行验证.
解:如图7—48所示.
3、【分析】
这是一个由若干条线段组成的图形,并且图7—49(1)中已经有两条与直线m垂直的线段,这是可以利用的.把图形画完整的关键在于画出B,D两点的对应点.
解:(1)如图7—49(2)所示,延长DF到D′,使FD′=DF,延长BH到点B′,使
B′H=BH.然后连接AB′,CD′,AB’,交FD’,于点E′,CD′交AB′于点G′.
(2)点E的对应点是点E′,线段GD的对应线段是G′D′,∠AEF的对应角是∠AE′F.
【解题策略】
解题之前必须认真地分析,就本题来说,如果不仔细分析,那么很容易去画点G的对应点,结果是既费时又费力.
达标测评
1、【分析】由轴对称图形的性质可确定C项正确.故选C.
探索轴对称的性质
【学习目标】
理解对应点所连的线段被对称轴垂直平分.
对应线段相等、对应角相等的性质.
【重点难点】
重点:理解“对应点所连的线段被对称轴垂直平分、对应线段相等、对应角相等”的性质.
难点:运用对称轴的性质
【学习过程】
情境导入
如下图所示,方格内的图形都是轴对称的,请画出它们的对称轴.
自主学习
一、掌握轴对称的性质
1.轴对称的性质
(1)对应点所连的线段被对称轴垂直平分;
(2)对应线段相等,对应角相等.
2.轴对称图形的性质
(1)轴对称图形对应点所连的线段被对称轴垂直平分;
(2)轴对称图形对应线段相等,对应角相等.
导学解疑:
一、展示点拨,归纳新知:
二、典例分析
1、如图7—50所示,DE是ΔABC的AB边的垂直平分线,分别交AB,BC于D,E,AE平分∠BAC,若∠B=30°,求∠C的度数.
三、巩固练习
1、如图
(1)所示,画出此轴对称图形的另一半(对称轴为l
).
2、如图7—47所示,八面彩旗构成了轴对称图形,请找出图形中与点A对
应的点,用A′表示出来.
3、如图(1)所示的是一个轴对称图形的一半,对称轴是直线m.
(1)把这个轴对称图形画完整;
(2)指出点E的对应点,线段GD的对应线段和∠AEF的对应角.
成果检验
一、达标测评
1、如图7—52所示的矩形纸片,先沿虚线按箭头方向向右对折,接着将对折后的纸片沿虚线剪下一个小圆和一个小三角形,然后将纸片打开,得到的图形是图7—53中的
(
)
二、总结延伸:
1.
本节课的收获:先由学生总结,老师启发补充
2.
本节课渗透的数学思想方法
3.
关于这一课的知识你还有不明白的地方吗?如果有请提出来,让老师和同学帮你解决。
答案
典例分析
1、【分析】由DE是AB边的垂直平分线,可知DE是ΔABE的对称轴,故对应角∠1=∠B。而AE是∠BAC的平分线,所以∠1=∠2.再由三角形内角和定理可求得∠C的度数.
解:因为DE是AB的垂直平分线,所以EA=EB,所以∠l=∠B.
又因为∠B=30°,所以∠1=30°.
因为AE平分∠BAC,所以∠2=∠1=30°,即∠BAC=60°.
所以∠C=180°-∠B-∠BAC=180°-30°-60°=90°.
【解题策略】
灵活运用线段垂直平分线、角平分线、三角形内角和的性质解决问题.
巩固练习
1、解:如图7—46(2)所示,过B点作l的垂线,取OB′=OB,B′是B点的对应点,同理找出C点的对应点C′,点A和D的对应点还是它本身,连接A′,B′,C′,D′,得到轴对称图形关于对称轴对称的另一半.
【解题策略】
解此题的关键是根据轴对称图形的性质画出关键点A,B,C,D关于直线l的对称点.
2、【分析】可以画出这个图形的对称轴,利用轴对称图形的性质进行判断.也可先
凭观察得出初步结论,然后进行验证.
解:如图7—48所示.
3、【分析】
这是一个由若干条线段组成的图形,并且图7—49(1)中已经有两条与直线m垂直的线段,这是可以利用的.把图形画完整的关键在于画出B,D两点的对应点.
解:(1)如图7—49(2)所示,延长DF到D′,使FD′=DF,延长BH到点B′,使
B′H=BH.然后连接AB′,CD′,AB’,交FD’,于点E′,CD′交AB′于点G′.
(2)点E的对应点是点E′,线段GD的对应线段是G′D′,∠AEF的对应角是∠AE′F.
【解题策略】
解题之前必须认真地分析,就本题来说,如果不仔细分析,那么很容易去画点G的对应点,结果是既费时又费力.
达标测评
1、【分析】由轴对称图形的性质可确定C项正确.故选C.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
