1.4 整式的乘法 学案（含答案）

1.4
整式的乘法
【学习目标】
单项式与单项式相乘
单项式与多项式相乘
多项式与多项式相乘
【重点难点】
1、单项式与单项式相乘
2、单项式与多项式相乘
【学习过程】
情境导入
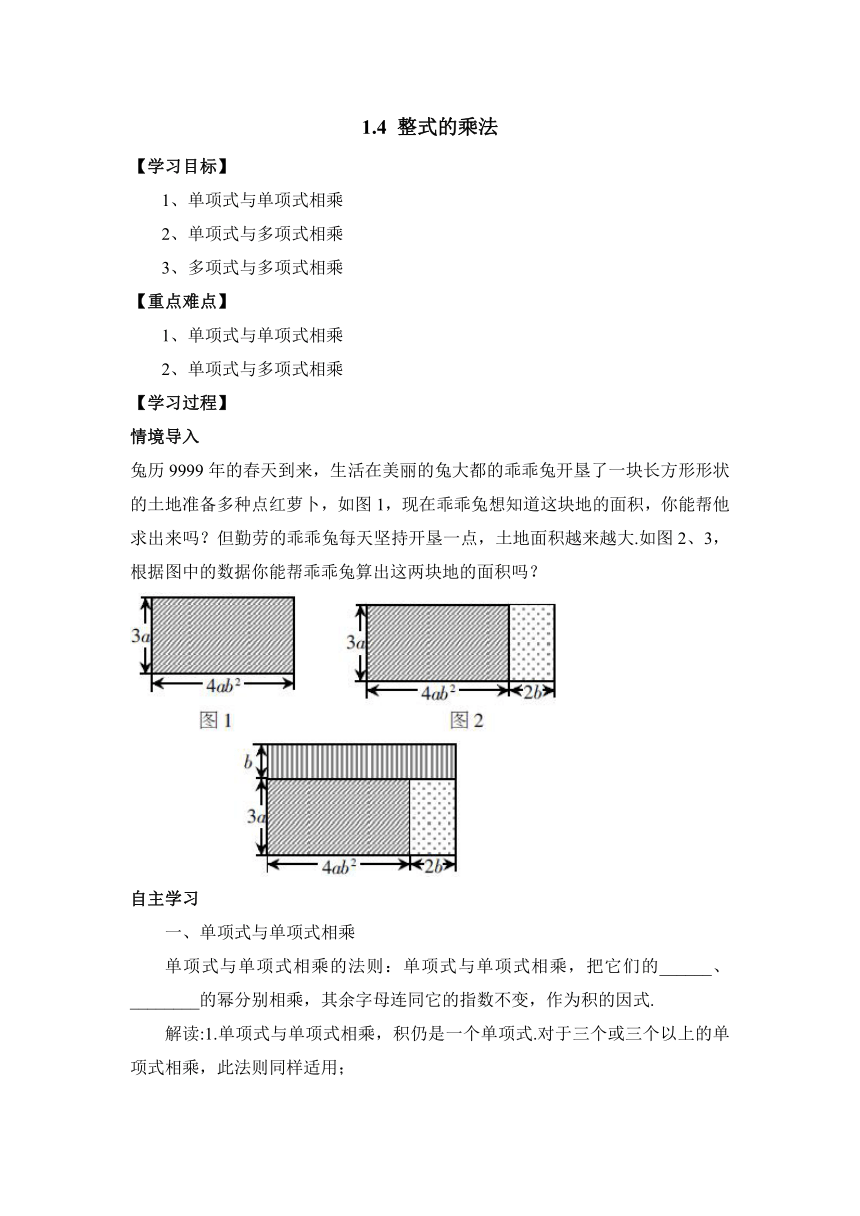
兔历9999年的春天到来，生活在美丽的兔大都的乖乖兔开垦了一块长方形形状的土地准备多种点红萝卜，如图1，现在乖乖兔想知道这块地的面积，你能帮他求出来吗？但勤劳的乖乖兔每天坚持开垦一点，土地面积越来越大.如图2、3，根据图中的数据你能帮乖乖兔算出这两块地的面积吗？
自主学习
一、单项式与单项式相乘
单项式与单项式相乘的法则：单项式与单项式相乘，把它们的______、________的幂分别相乘，其余字母连同它的指数不变，作为积的因式.
解读:1.单项式与单项式相乘，积仍是一个单项式.对于三个或三个以上的单项式相乘，此法则同样适用；
2.单项式与单项式相乘时，要先把各个单项式的系数相乘，作为积的系数，同时要注意系数的符号；
3.相同字母的幂相乘，实际上就是按照同底数幂的乘法法则进行，即底数不变，指数相加；
4.对于只在一个单项式里含有的字母，一定要把它连同指数写在积中，作为积的一个因式，切记不要将它漏掉.
二、单项式与多项式相乘
单项式与多项式相乘的法则：单项式与多项式相乘，就是根据分配律用单项式去乘多项式的______，再把所得的积______.
解读:1.该法则的实质是将单项式与多项式的相乘转化为单项式与单项式相乘；
法则中“每一项”的含义是无重无漏.在运算时，要按照一定的顺序进行，否则容易造成漏项或增项的错误，特别要注意多项式中的常数项；
在运算过程中，要注意各项的符号，尤其是负号的情形；
单项式与多项式相乘的结果仍是一个多项式，积的项数与多项式中的项数相同.
三、多项式与多项式相乘
多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的__________乘另一个多项式的______，再把所得的积_____.
解读:1.理解法则中两个“每一项”的含义，它们同样都是无重无漏.在运算过程中，严格按照多项式与多项式相乘的法则，先把一个多项式作为一个整体，去乘另一个多项式的每一项，即转化为单项式与多项式相乘.在合并同类项之前，积的项数是两个多项式的项数之积；
在运算过程中，要注意各项的符号，尤其是负号的情形；
最后结果一定要化成最简形式，是同类项的一定要合并.
四、掌握整式乘法运算中的数学思想
1.化归思想：多项式与多项式相乘都是化归为多项式乘以单项式来完成的，多项式与单项式相乘又是化归为单项式与单项式相乘来完成的，而单项式与单项式又可以化归为同底数幂的乘法运算来完成；
2.整体思想:在进行幂的运算和整式的乘法运算时经常要用到整体思想.
导学解疑：
展示点拨，归纳新知
二、典例分析
1、一个三位数，其十位数字比个位数字大1，百位数字又比十位数字大2．另外有一个两位数，其十位数字与三位数的个位数字相同，都可用a表示，其个位数字比十位数字小3，请把这两个数之积用含a的代数式表示出来，并把此代数式化简．若a＝4，把这两个数表示出来．
2、当m，n为何值时，x
[x
(x+m)+nx(x+1)+m]的展开式中不含x2项和x3项
三、巩固练习
1、计算．
（1）（2xy2）·；
（2）（-2
a2
b3）·(-3
a)
（3）（4×105）×(5×104)；
（4）5
a2
bx·(-3
a
b3
x
y2).
2、计算
(1)(2x-5y)(3x-5y+6)；
(2)(
a2-2
b2)(
a+2
b)-2ab(a-b)；
(3)[(-3x3)
2-(2x3)
2+(-3x2)(-x2)
2](5x-1)；
(4)2(3x-2y)(x+5y)-6(x-y)(3x+2y)．
3、求x
(x2+
x-3)
-
x2
(x-1)-2(x-1)(2
x+1)+2
x2的值，其中x＝100．
4、一个三位数，其十位数字比个位数字大1，百位数字又比十位数字大2．另外有一个两位数，其十位数字与三位数的个位数字相同，都可用a表示，其个位数字比十位数字小3，请把这两个数之积用含a的代数式表示出来，并把此代数式化简．若a＝4，把这两个数表示出来．
成果检验一、达标测评
1、化简(-3
x2)·2
x3的结果是
(
)
A．-6
x5
B．-3
x5
C．2
x5
D．6
x5
2、(-2a)·=
.
答案
自主学习
系数；相同字母；每一项；相加；每一项；每一项；相加
典例分析
1、解：三位数的个位数字为a，则十位数字为a+1，百位数字为(a+1)+2＝a+3，此三位数用代数式表示为100(a+3)+10(a+1)+
a．两位数的十位数字为a，其个位数字为a-3，则此两位数用代数式表示为10a+(a-3)．
两个数的乘积为[100(a+3)+10(a+1)+a][10a+(a-3)]＝(100a+300+10a+10+a)·(10a+a-3)＝(111a+310)(11a-3)＝1221a2+3410a-333a-930＝1221a2+3077a-930．
当a＝4时，三位数为754，两位数为41．
【解题策略】
准确用字母表示出三位数、两位数是解此题的关键
2、分析
遇到这类问题，只需用单项式与多项式相乘，展开后，合并同类项，然后使不存在的项的系数为零．
解：x
[x
(x+m)+nx(x+1)+m]＝x
(x2+mx+n
x2+nx+m)＝x3+m
x2+n
x3
+n
x2
+m
x=x3+x2+mx.=
（1+n）x2
+（m+n）x2
+mx
因为多项式中不含x2项和x3项．
所以解得
【解题策略】
此种类型题若是多项式乘多项式，解法相同
巩固练习
1、分析
计算积的系数时，先确定其符号再求其绝对值；单项式乘早项式的结果仍是单项式，只在一个早项式里出现的因式，必须连同它的指数作为积的一个因式．
解：（1）（2xy2）·=·（x·x）·（y2·y）=x2
y3.
（2）（-2
a2
b3）·(-3
a)=[(-2)
×(-3)]·（a2·a）·b3=6
a3
b3.
（3）（4×105）×(5×104)=(4×5)
×(105×104)=20×109=2×1010.
（4）5
a2
bx·(-3
a
b3
x
y2)=[5×(-3)](
a2·a)（b·b3）(x·x)
y2=-15
a3
b4
x2
y2.
【解题策略】
注意单项式与单项式相乘性质的准确运用．
2、解：(1)原式＝6x2-15xy-10xy+25y2+12x-30y＝6x2-25xy+25y2+12x-30y．
(2)原式＝a3-2ab2+2
a2b-4
b3-2
a2b+2
ab2＝a3-4
b3．
(3)原式＝(9
x2-4x6-3x6)(5
x-1)＝2
x6
(5
x-1)＝10
x7-2
x6．
(4)原式＝2(3
x2+13
x
y-10
y2)-6(3
x2-
x
y-2
y2)＝-12
x2+32xy-8
y2．
【解题策略】带“-”号的单项式乘多项式时，一定要注意符号的变化．
3、分析
本题是单项式和多项式的混合乘法，应用整式的乘法法则计算后合并同类项，最后求值．
解：原式＝x3+
x2-3x-
x3
+x2-2(2
x2-
x-1)+2
x2＝-
x+2．
当x＝100时，原式＝-100+2＝-98．
【解题策略】
括号前面带“-”号的因式与括号内各项相乘时，要注意括号内的各项都要变号．
达标测评
1、分析
(-3
x2)·2
x3＝(-3)×2
x2+3＝-6
x5．故选A．
2、分析
本题考查整式的计算．(一2a)·=-a4+2a.故填-a4+2a.