2017年秋冀教版数学九年级上第26章 解直角三角形 达标检测卷(含答案)
文档属性
| 名称 | 2017年秋冀教版数学九年级上第26章 解直角三角形 达标检测卷(含答案) | 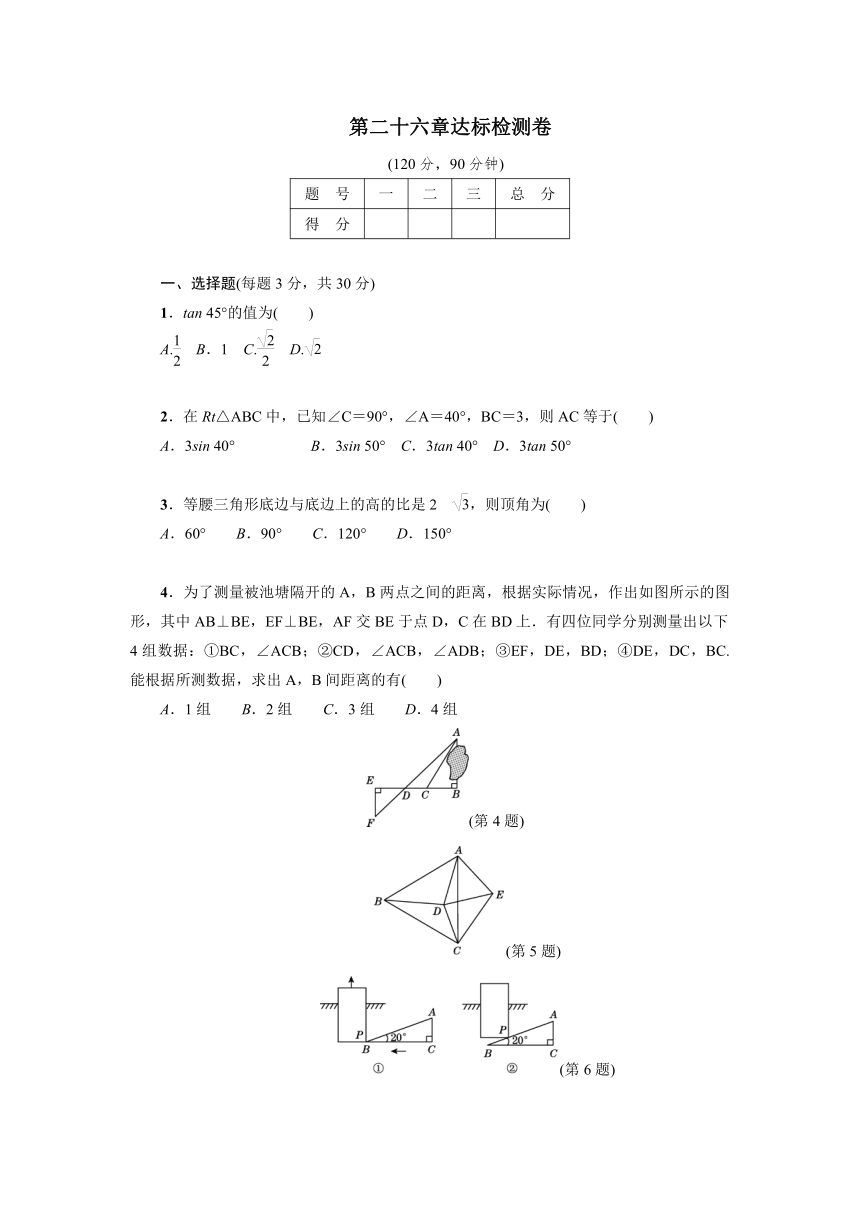 | |
| 格式 | zip | ||
| 文件大小 | 219.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-12 23:32:16 | ||
图片预览



文档简介
第二十六章达标检测卷
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.tan
45°的值为( )
A.
B.1
C.
D.
2.在Rt△ABC中,已知∠C=90°,∠A=40°,BC=3,则AC等于( )
A.3sin
40°
B.3sin
50°
C.3tan
40°
D.3tan
50°
3.等腰三角形底边与底边上的高的比是2?,则顶角为( )
A.60°
B.90°
C.120°
D.150°
4.为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有( )
A.1组
B.2组
C.3组
D.4组
INCLUDEPICTURE
"../../../95.tif"
\
MERGEFORMAT
(第4题)
INCLUDEPICTURE
"../../../CD7.tif"
\
MERGEFORMAT
(第5题)
INCLUDEPICTURE
"../../../BV29.tif"
\
MERGEFORMAT
(第6题)
5.如图,在等边三角形ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕点A逆时针旋转,使AB与AC重合,点D旋转到点E,则tan∠CDE的值是( )
A.
B.3
C.
D.
6.如图①,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩竖直向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8
cm(如图②),则木桩大约上升了(结果保留一位小数.参考数据:sin
20°≈0.34,cos
20°≈0.94,tan
20°≈0.36)( )
A.2.9
cm
B.2.2
cm
C.2.7
cm
D.7.5
cm
7.如图,已知在四边形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
A.
B.4
C.
D.4
8.李红同学遇到了这样一道题:求tan
(α+20°)=1中锐角α的度数.你认为锐角α的度数应是( )
A.40°
B.30°
C.20°
D.10°
9.如图,某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距20
n
mile.客轮以60
n
mile/h的速度沿北偏西60°方向航行
h到达B处,那么tan∠ABP的值等于( )
A.
B.2
C.
D.
INCLUDEPICTURE
"../../../97.tif"
\
MERGEFORMAT
(第7题)
INCLUDEPICTURE
"../../../BV41.tif"
\
MERGEFORMAT
(第9题)
INCLUDEPICTURE
"../../../98.tif"
\
MERGEFORMAT
(第10题)
10.如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60
cm,若AO=100
cm,则墙角O到前沿BC的距离OE是( )
A.(60+100sin
α)
cm
B.(60+100cos
α)
cm
C.(60+100tan
α)
cm
D.以上选项都不对
二、填空题(每题3分,共24分)
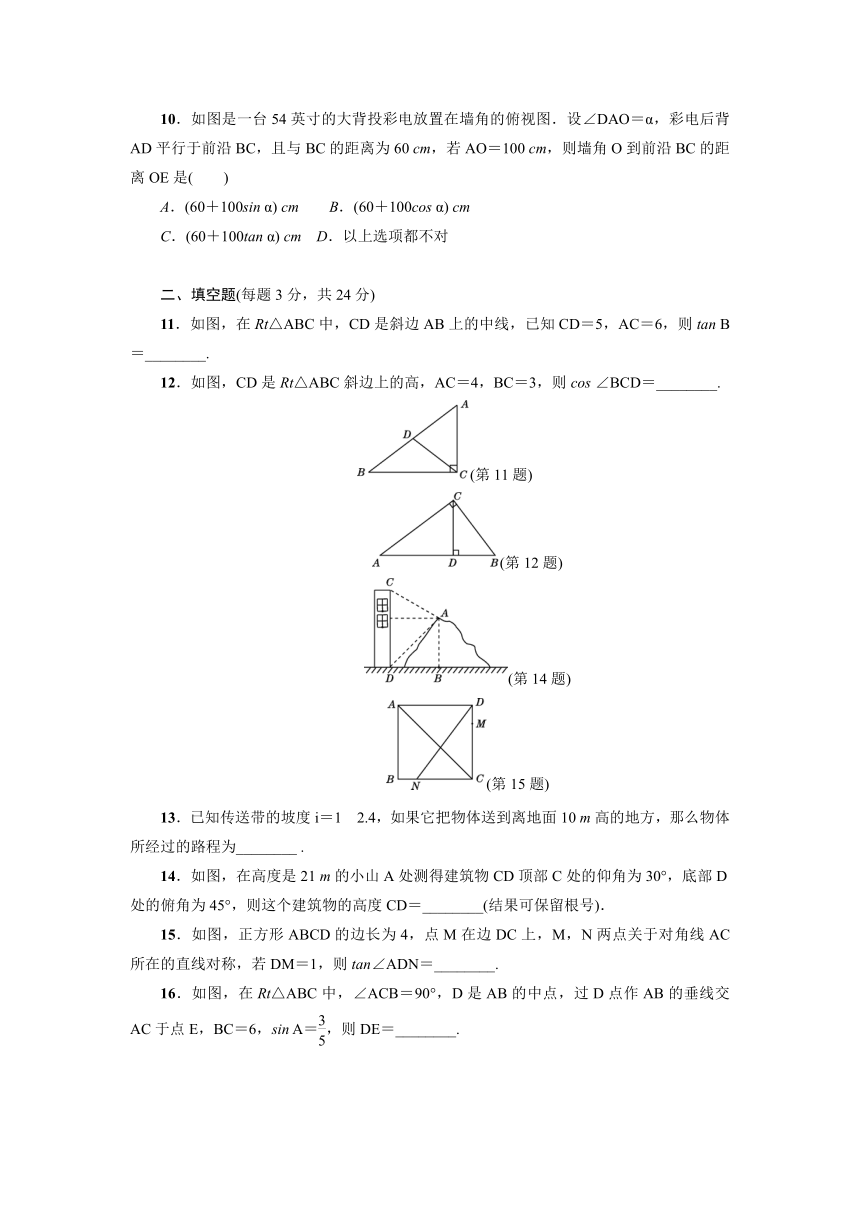
11.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan
B=________.
12.如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos
∠BCD=________.
INCLUDEPICTURE
"../../../99.tif"
\
MERGEFORMAT
(第11题)
INCLUDEPICTURE
"../../../100.tif"
\
MERGEFORMAT
(第12题)
INCLUDEPICTURE
"../../../101.tif"
\
MERGEFORMAT
(第14题)
INCLUDEPICTURE
"../../../TH97.tif"
\
MERGEFORMAT
(第15题)
13.已知传送带的坡度i=1?2.4,如果它把物体送到离地面10
m高的地方,那么物体所经过的路程为________
.
14.如图,在高度是21
m的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=________(结果可保留根号).
15.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC所在的直线对称,若DM=1,则tan∠ADN=________.
16.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sin
A=,则DE=________.
INCLUDEPICTURE
"../../../103.tif"
\
MERGEFORMAT
(第16题)
INCLUDEPICTURE
"../../../TH96.tif"
\
MERGEFORMAT
(第17题)
INCLUDEPICTURE
"../../../105.tif"
\
MERGEFORMAT
(第18题)
17.如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30
m/min的速度沿与地面成75°角的方向飞行,25
min后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A,B两点间的距离为__________.
18.如图,在东西方向的海岸线上有A,B两个港口,甲货船从A港出发,沿北偏东60°的方向以4
n
mile/h的速度航行,同时乙货船从B港出发,沿西北方向航行,2
h后两船在点P处相遇,则乙货船的速度为____________.
三、解答题(19,20题每题12分,其余每题14分,共66分)
19.计算:(1)2-1-tan
60°+(π-2
015)0+;
(2)(π-)0++(-1)2
015-tan
60°.
20.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物方向前进了100
m到达B处,此时测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5
m,请你计算出该建筑物的高度(结果精确到1
m.参考数据:≈1.732).
INCLUDEPICTURE
"../../../106.tif"
\
MERGEFORMAT
(第20题)
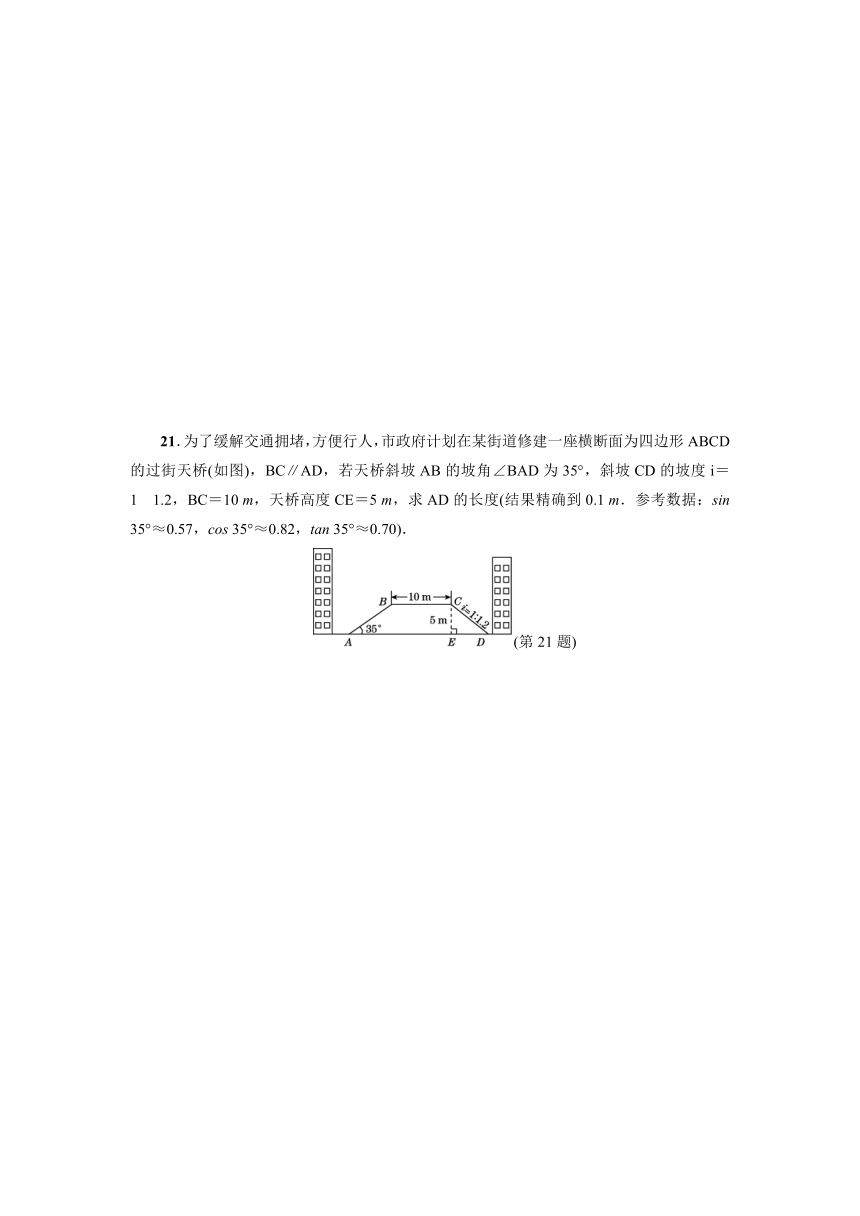
21.为了缓解交通拥堵,方便行人,市政府计划在某街道修建一座横断面为四边形ABCD的过街天桥(如图),BC∥AD,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度i=1?1.2,BC=10
m,天桥高度CE=5
m,求AD的长度(结果精确到0.1
m.参考数据:sin
35°≈0.57,cos
35°≈0.82,tan
35°≈0.70).
INCLUDEPICTURE
"../../../BV42.tif"
\
MERGEFORMAT
(第21题)
22.如图是由6个形状、大小完全相同的小矩形组成的,小矩形的顶点称为格点.已知小矩形较短边长为1,△ABC的顶点都在格点上.
(1)用无刻度的直尺作图:找出格点D,连接CD,使∠ACD=90°;
(2)在(1)的条件下,连接AD,求tan
∠BAD的值.
INCLUDEPICTURE
"../../../BV43.tif"
\
MERGEFORMAT
(第22题)
23.小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136
cm,OA=OC=51
cm,OE=OF=34
cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32
cm(参考数据:sin
61.9°≈0.882,cos
61.9°≈0.471,tan
28.1°≈0.534).
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°);
(3)小红的连衣裙穿在晒衣架上的总长度达到122
cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
INCLUDEPICTURE
"../../../TH98.tif"
\
MERGEFORMAT
(第23题)
答案
一、1.B 2.D
3.A
4.C 点拨:对于①,可由AB=BC·tan
∠ACB求出A,B两点间的距离;对于②,由BC=,BD=,BD-BC=CD,可求出AB的长;对于③,易知△DEF∽△DBA,则=,可求出AB的长;对于④无法求得AB的长,故有①②③共3组,故选C.
5.B 6.A
7.A
点拨:过点A作AE⊥BC于点E,过D作DF⊥BC,交BC延长线于点F,解Rt△ABE可得AE=4,易证DF=AE,∴DF=4,再解Rt△DCF即可求出CD.
8.D 9.A 10.A
二、11. 12. 13.26
m
14.(7+21)
m 15. 16.
17.750
m 点拨:过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75°-30°=45°,AC=30×25=750(m),
∴AD=AC·sin
45°=375(m).
在Rt△ABD中,∵∠B=30°,∴AB=2AD=750(m).
即小山东西两侧A,B两点间的距离为750
m.
18.2
n
mile/h 点拨:如图,作PC⊥AB于点C.∵甲货船从A港出发,沿北偏东60°的方向以4
n
mile/h的速度航行,∴∠PAC=30°,AP=4×2=8(n
mile).∴PC=AP·sin
30°=8×=4(n
mile).∵乙货船从B港出发,沿西北方向航行,∴∠PBC=45°.∴PB=PC÷=4(n
mile).∴乙货船的速度为4÷2=2(n
mile/h).
INCLUDEPICTURE
"../../../169A.tif"
\
MERGEFORMAT
(第18题)
三、19.解:(1)2-1-tan
60°+(π-2
015)0+=-3+1+=-1.
(2)(π-)0++(-1)2
015-tan
60°=1+2-1-3=-1.
20.解:设CE=x
m.由题意可知,△BCE为等腰直角三角形.∴BE=CE=x
m.在Rt△AEC中,tan
∠CAE=,即tan
30°=,∴=.解得x≈136.6.∴CD=CE+ED≈138
m.故该建筑物的高度约为138
m.
21.解:过点B作BF⊥AD于点F,则四边形BFEC是矩形,
∴BF=CE=5
m,EF=BC=10
m.
在Rt△ABF中,∠BAF=35°,tan∠BAF=,
∴AF=≈≈7.14(m).
∵斜坡CD的坡度i=1∶1.2,
∴=.∴ED=1.2CE=1.2×5=6(m).
∴AD=AF+FE+ED≈7.14+10+6≈23.1(m).
故AD的长度约为23.1
m.
22.解:(1)如图.
INCLUDEPICTURE
"../../../BV47.tif"
\
MERGEFORMAT
(第22题)
(2)如图,连接BD,
∵∠BED=90°,BE=DE=1,
∴∠EBD=∠EDB=45°,
BD===.
易知BF=AF=2,∠BFA=90°.∴∠ABF=∠BAF=45°,AB===2,
∴∠ABD=∠ABF+∠EBD=45°+45°=90°.
∴tan
∠BAD===.
23.(1)证明:方法一:∵AB,CD相交于点O,
∴∠AOC=∠BOD.
∵OA=OC,∴∠OAC=∠OCA=(180°-∠AOC).
同理∠OBD=∠ODB=(180°-∠BOD).
∴∠OAC=∠OBD.∴AC∥BD.
方法二:∵AB=CD=136
cm,
OA=OC=51
cm,
∴OB=OD=85
cm.∴==.
又∵∠AOC=∠BOD,∴△AOC∽△BOD.
∴∠OAC=∠OBD.∴AC∥BD.
(2)解:在△OEF中,OE=OF=34
cm,EF=32
cm.
如图,作OM⊥EF于点M,则EM=16
cm.
∴cos∠OEF==≈0.471.
∴∠OEF≈61.9°.
INCLUDEPICTURE
"../../../th103.tif"
\
MERGEFORMAT
(第23题)
(3)解:方法一:小红的连衣裙垂挂在晒衣架上会拖落到地面.
理由如下:如图,过A作AH⊥BD于点H.
在Rt△OEM中,
OM===30(cm).
易证∠ABD=∠OEM.
∵∠OME=∠AHB=90°,
∴△OEM∽△ABH.
∴=.∴AH===120(cm).
∵小红的连衣裙穿在晒衣架上的总长度122
cm大于晒衣架的高度120
cm,
∴小红的连衣裙垂挂在晒衣架上会拖落到地面.
方法二:小红的连衣裙垂挂在晒衣架上会拖落到地面.理由如下:
易得∠ABD=∠OEF≈61.9°.
如图,过点A作AH⊥BD于点H.
在Rt△ABH中,∵sin∠ABD=,
∴AH=AB·sin∠ABD≈136×sin
61.9°≈136×0.882≈120(cm).
∵小红的连衣裙穿在晒衣架上的总长度122
cm大于晒衣架的高度120
cm,
∴小红的连衣裙垂挂在晒衣架上会拖落到地面.
(120分,90分钟)
题 号
一
二
三
总 分
得 分
一、选择题(每题3分,共30分)
1.tan
45°的值为( )
A.
B.1
C.
D.
2.在Rt△ABC中,已知∠C=90°,∠A=40°,BC=3,则AC等于( )
A.3sin
40°
B.3sin
50°
C.3tan
40°
D.3tan
50°
3.等腰三角形底边与底边上的高的比是2?,则顶角为( )
A.60°
B.90°
C.120°
D.150°
4.为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示的图形,其中AB⊥BE,EF⊥BE,AF交BE于点D,C在BD上.有四位同学分别测量出以下4组数据:①BC,∠ACB;②CD,∠ACB,∠ADB;③EF,DE,BD;④DE,DC,BC.能根据所测数据,求出A,B间距离的有( )
A.1组
B.2组
C.3组
D.4组
INCLUDEPICTURE
"../../../95.tif"
\
MERGEFORMAT
(第4题)
INCLUDEPICTURE
"../../../CD7.tif"
\
MERGEFORMAT
(第5题)
INCLUDEPICTURE
"../../../BV29.tif"
\
MERGEFORMAT
(第6题)
5.如图,在等边三角形ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕点A逆时针旋转,使AB与AC重合,点D旋转到点E,则tan∠CDE的值是( )
A.
B.3
C.
D.
6.如图①,将一个Rt△ABC形状的楔子从木桩的底端点P处沿水平方向打入木桩底下,使木桩竖直向上运动,已知楔子斜面的倾斜角为20°,若楔子沿水平方向前移8
cm(如图②),则木桩大约上升了(结果保留一位小数.参考数据:sin
20°≈0.34,cos
20°≈0.94,tan
20°≈0.36)( )
A.2.9
cm
B.2.2
cm
C.2.7
cm
D.7.5
cm
7.如图,已知在四边形ABCD中,AD∥BC,∠B=45°,∠C=120°,AB=8,则CD的长为( )
A.
B.4
C.
D.4
8.李红同学遇到了这样一道题:求tan
(α+20°)=1中锐角α的度数.你认为锐角α的度数应是( )
A.40°
B.30°
C.20°
D.10°
9.如图,某时刻海上点P处有一客轮,测得灯塔A位于P的北偏东30°方向,且相距20
n
mile.客轮以60
n
mile/h的速度沿北偏西60°方向航行
h到达B处,那么tan∠ABP的值等于( )
A.
B.2
C.
D.
INCLUDEPICTURE
"../../../97.tif"
\
MERGEFORMAT
(第7题)
INCLUDEPICTURE
"../../../BV41.tif"
\
MERGEFORMAT
(第9题)
INCLUDEPICTURE
"../../../98.tif"
\
MERGEFORMAT
(第10题)
10.如图是一台54英寸的大背投彩电放置在墙角的俯视图.设∠DAO=α,彩电后背AD平行于前沿BC,且与BC的距离为60
cm,若AO=100
cm,则墙角O到前沿BC的距离OE是( )
A.(60+100sin
α)
cm
B.(60+100cos
α)
cm
C.(60+100tan
α)
cm
D.以上选项都不对
二、填空题(每题3分,共24分)
11.如图,在Rt△ABC中,CD是斜边AB上的中线,已知CD=5,AC=6,则tan
B=________.
12.如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,则cos
∠BCD=________.
INCLUDEPICTURE
"../../../99.tif"
\
MERGEFORMAT
(第11题)
INCLUDEPICTURE
"../../../100.tif"
\
MERGEFORMAT
(第12题)
INCLUDEPICTURE
"../../../101.tif"
\
MERGEFORMAT
(第14题)
INCLUDEPICTURE
"../../../TH97.tif"
\
MERGEFORMAT
(第15题)
13.已知传送带的坡度i=1?2.4,如果它把物体送到离地面10
m高的地方,那么物体所经过的路程为________
.
14.如图,在高度是21
m的小山A处测得建筑物CD顶部C处的仰角为30°,底部D处的俯角为45°,则这个建筑物的高度CD=________(结果可保留根号).
15.如图,正方形ABCD的边长为4,点M在边DC上,M,N两点关于对角线AC所在的直线对称,若DM=1,则tan∠ADN=________.
16.如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sin
A=,则DE=________.
INCLUDEPICTURE
"../../../103.tif"
\
MERGEFORMAT
(第16题)
INCLUDEPICTURE
"../../../TH96.tif"
\
MERGEFORMAT
(第17题)
INCLUDEPICTURE
"../../../105.tif"
\
MERGEFORMAT
(第18题)
17.如图,在小山的东侧A点有一个热气球,由于受西风的影响,以30
m/min的速度沿与地面成75°角的方向飞行,25
min后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A,B两点间的距离为__________.
18.如图,在东西方向的海岸线上有A,B两个港口,甲货船从A港出发,沿北偏东60°的方向以4
n
mile/h的速度航行,同时乙货船从B港出发,沿西北方向航行,2
h后两船在点P处相遇,则乙货船的速度为____________.
三、解答题(19,20题每题12分,其余每题14分,共66分)
19.计算:(1)2-1-tan
60°+(π-2
015)0+;
(2)(π-)0++(-1)2
015-tan
60°.
20.如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物方向前进了100
m到达B处,此时测得建筑物顶部的仰角是45°.已知测角仪的高度是1.5
m,请你计算出该建筑物的高度(结果精确到1
m.参考数据:≈1.732).
INCLUDEPICTURE
"../../../106.tif"
\
MERGEFORMAT
(第20题)
21.为了缓解交通拥堵,方便行人,市政府计划在某街道修建一座横断面为四边形ABCD的过街天桥(如图),BC∥AD,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度i=1?1.2,BC=10
m,天桥高度CE=5
m,求AD的长度(结果精确到0.1
m.参考数据:sin
35°≈0.57,cos
35°≈0.82,tan
35°≈0.70).
INCLUDEPICTURE
"../../../BV42.tif"
\
MERGEFORMAT
(第21题)
22.如图是由6个形状、大小完全相同的小矩形组成的,小矩形的顶点称为格点.已知小矩形较短边长为1,△ABC的顶点都在格点上.
(1)用无刻度的直尺作图:找出格点D,连接CD,使∠ACD=90°;
(2)在(1)的条件下,连接AD,求tan
∠BAD的值.
INCLUDEPICTURE
"../../../BV43.tif"
\
MERGEFORMAT
(第22题)
23.小红家的阳台上放置了一个晒衣架(如图①),图②是晒衣架的侧面示意图,立杆AB,CD相交于点O,B,D两点立于地面,经测量:AB=CD=136
cm,OA=OC=51
cm,OE=OF=34
cm,现将晒衣架完全稳固张开,扣链EF成一条线段,且EF=32
cm(参考数据:sin
61.9°≈0.882,cos
61.9°≈0.471,tan
28.1°≈0.534).
(1)求证:AC∥BD;
(2)求扣链EF与立杆AB的夹角∠OEF的度数(结果精确到0.1°);
(3)小红的连衣裙穿在晒衣架上的总长度达到122
cm,垂挂在晒衣架上是否会拖落到地面?请通过计算说明理由.
INCLUDEPICTURE
"../../../TH98.tif"
\
MERGEFORMAT
(第23题)
答案
一、1.B 2.D
3.A
4.C 点拨:对于①,可由AB=BC·tan
∠ACB求出A,B两点间的距离;对于②,由BC=,BD=,BD-BC=CD,可求出AB的长;对于③,易知△DEF∽△DBA,则=,可求出AB的长;对于④无法求得AB的长,故有①②③共3组,故选C.
5.B 6.A
7.A
点拨:过点A作AE⊥BC于点E,过D作DF⊥BC,交BC延长线于点F,解Rt△ABE可得AE=4,易证DF=AE,∴DF=4,再解Rt△DCF即可求出CD.
8.D 9.A 10.A
二、11. 12. 13.26
m
14.(7+21)
m 15. 16.
17.750
m 点拨:过点A作AD⊥BC,垂足为D,在Rt△ACD中,∠ACD=75°-30°=45°,AC=30×25=750(m),
∴AD=AC·sin
45°=375(m).
在Rt△ABD中,∵∠B=30°,∴AB=2AD=750(m).
即小山东西两侧A,B两点间的距离为750
m.
18.2
n
mile/h 点拨:如图,作PC⊥AB于点C.∵甲货船从A港出发,沿北偏东60°的方向以4
n
mile/h的速度航行,∴∠PAC=30°,AP=4×2=8(n
mile).∴PC=AP·sin
30°=8×=4(n
mile).∵乙货船从B港出发,沿西北方向航行,∴∠PBC=45°.∴PB=PC÷=4(n
mile).∴乙货船的速度为4÷2=2(n
mile/h).
INCLUDEPICTURE
"../../../169A.tif"
\
MERGEFORMAT
(第18题)
三、19.解:(1)2-1-tan
60°+(π-2
015)0+=-3+1+=-1.
(2)(π-)0++(-1)2
015-tan
60°=1+2-1-3=-1.
20.解:设CE=x
m.由题意可知,△BCE为等腰直角三角形.∴BE=CE=x
m.在Rt△AEC中,tan
∠CAE=,即tan
30°=,∴=.解得x≈136.6.∴CD=CE+ED≈138
m.故该建筑物的高度约为138
m.
21.解:过点B作BF⊥AD于点F,则四边形BFEC是矩形,
∴BF=CE=5
m,EF=BC=10
m.
在Rt△ABF中,∠BAF=35°,tan∠BAF=,
∴AF=≈≈7.14(m).
∵斜坡CD的坡度i=1∶1.2,
∴=.∴ED=1.2CE=1.2×5=6(m).
∴AD=AF+FE+ED≈7.14+10+6≈23.1(m).
故AD的长度约为23.1
m.
22.解:(1)如图.
INCLUDEPICTURE
"../../../BV47.tif"
\
MERGEFORMAT
(第22题)
(2)如图,连接BD,
∵∠BED=90°,BE=DE=1,
∴∠EBD=∠EDB=45°,
BD===.
易知BF=AF=2,∠BFA=90°.∴∠ABF=∠BAF=45°,AB===2,
∴∠ABD=∠ABF+∠EBD=45°+45°=90°.
∴tan
∠BAD===.
23.(1)证明:方法一:∵AB,CD相交于点O,
∴∠AOC=∠BOD.
∵OA=OC,∴∠OAC=∠OCA=(180°-∠AOC).
同理∠OBD=∠ODB=(180°-∠BOD).
∴∠OAC=∠OBD.∴AC∥BD.
方法二:∵AB=CD=136
cm,
OA=OC=51
cm,
∴OB=OD=85
cm.∴==.
又∵∠AOC=∠BOD,∴△AOC∽△BOD.
∴∠OAC=∠OBD.∴AC∥BD.
(2)解:在△OEF中,OE=OF=34
cm,EF=32
cm.
如图,作OM⊥EF于点M,则EM=16
cm.
∴cos∠OEF==≈0.471.
∴∠OEF≈61.9°.
INCLUDEPICTURE
"../../../th103.tif"
\
MERGEFORMAT
(第23题)
(3)解:方法一:小红的连衣裙垂挂在晒衣架上会拖落到地面.
理由如下:如图,过A作AH⊥BD于点H.
在Rt△OEM中,
OM===30(cm).
易证∠ABD=∠OEM.
∵∠OME=∠AHB=90°,
∴△OEM∽△ABH.
∴=.∴AH===120(cm).
∵小红的连衣裙穿在晒衣架上的总长度122
cm大于晒衣架的高度120
cm,
∴小红的连衣裙垂挂在晒衣架上会拖落到地面.
方法二:小红的连衣裙垂挂在晒衣架上会拖落到地面.理由如下:
易得∠ABD=∠OEF≈61.9°.
如图,过点A作AH⊥BD于点H.
在Rt△ABH中,∵sin∠ABD=,
∴AH=AB·sin∠ABD≈136×sin
61.9°≈136×0.882≈120(cm).
∵小红的连衣裙穿在晒衣架上的总长度122
cm大于晒衣架的高度120
cm,
∴小红的连衣裙垂挂在晒衣架上会拖落到地面.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
