21.3.3 几何问题 课件
图片预览







文档简介
课件22张PPT。几何问题 1.一般三角形的面积公式是什么?
2.平行四边形的面积公式是什么?
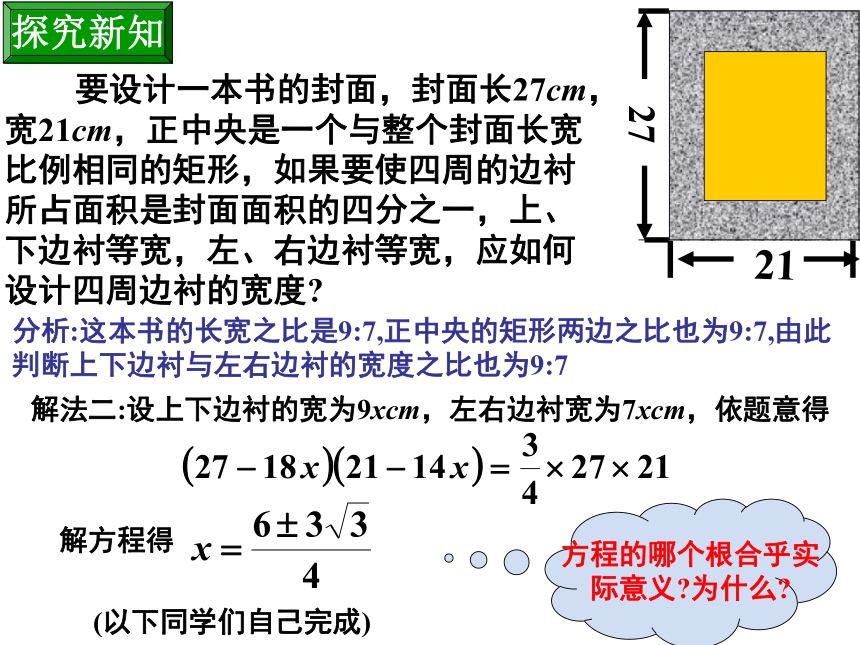
3.圆的面积公式是什么? 复习回顾 要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?分析:这本书的长宽之比是9:7,依题知正中央的矩形两边之比也为9:7解法一:设正中央的矩形两边分别为9xcm,7xcm
依题意得解得 故上下边衬的宽度为:
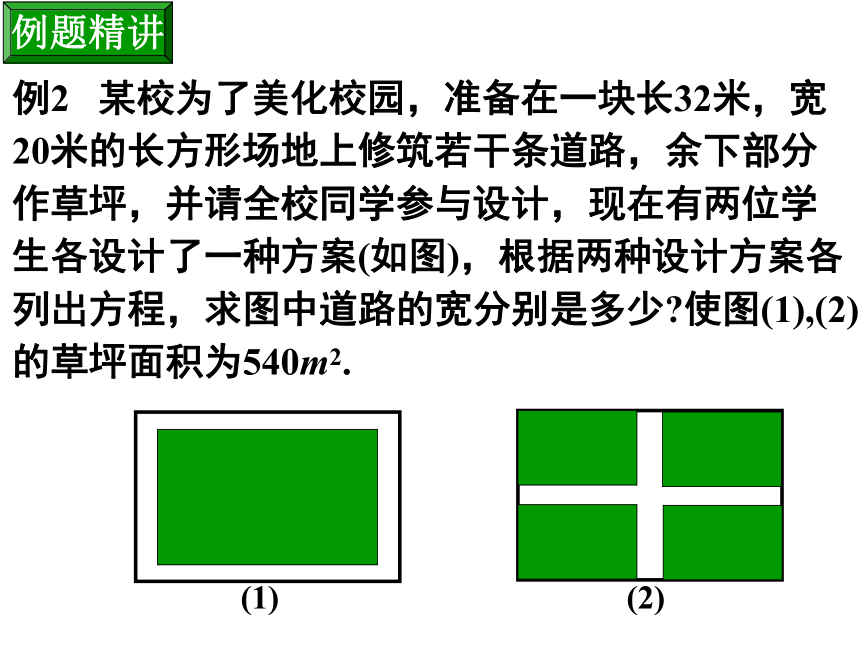
左右边衬的宽度为:探究新知分析:这本书的长宽之比是9:7,正中央的矩形两边之比也为9:7,由此判断上下边衬与左右边衬的宽度之比也为9:7解法二:设上下边衬的宽为9xcm,左右边衬宽为7xcm,依题意得解方程得(以下同学们自己完成)方程的哪个根合乎实际意义?为什么? 要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?探究新知例1 (2004年,镇江)学校为了美化校园环境,在一块长40米、宽20米的长方形空地上计划新建一块长9米、宽7米的长方形花圃. 在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.学以致用解: 在长方形花圃周长不变的情况下,长方形花圃面积不能增加2平方米.由题意得长方形长与宽的和为16米.设长方形花圃的长为x米,则宽为(16-x)米.x(16-x)=63+2, x2-16x+65=0,∴此方程无解.∴在周长不变的情况下,长方形花圃的面积不能增加2平方米学以致用1、用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.解:设这个矩形的长为xcm,则宽为 cm,即x2-10x+30=0这里a=1,b=-10,c=30,∴此方程无解.∴用20cm长的铁丝不能折成面积为30cm2的矩形.巩固练习例2 某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少?使图(1),(2)的草坪面积为540m2.例题精讲解:(1)如图,设道路的宽为x米,则化简得,其中的 x=25超出了原矩形的宽,应舍去.∴图(1)中道路的宽为1米.例题精讲则横向的路面面积为 ,分析:此题的相等关系是矩形面积减去道路面积等于540m2。解法一、 如图,设道路的宽为x米,32x m2纵向的路面面积为 。20x m2注意:这两个面积的重叠部分是 x2m2?学以致用其中的 x=50超出了原矩形的长和宽,应舍去.
取x=2时,道路总面积为:答:所求道路的宽为2m。学以致用解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)学以致用横向路面 ,如图,设路宽为x米,32xm2纵向路面面积为 。20xm2草坪矩形的长(横向)为 ,草坪矩形的宽(纵向) 。相等关系是:草坪长×草坪宽=540m2(20-x)m(32-x)m再往下的计算、格式书写与解法1相同。学以致用2.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?解:设道路宽为x米,则化简得,其中的 x=35超出了原矩形的宽,应舍去.答:道路的宽为1米.巩固练习3.如图,长方形ABCD,AB=15m,BC=20m,四周外围环绕着宽度相等的小路,已知小路的面积为246m2,求小路的宽度.解:设小路宽为x米,则化简得,答:小路的宽为3米.巩固练习例3 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米,面积为S平方米,
(1)求S与x的函数关系式;(2)如果要围成面积为45米2的花圃,AB的长是多少米?学以致用4.如图,用长为18m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.要围成苗圃的面积为81m2,应该怎么设计?解:设苗圃的一边长为xm,则化简得,答:应围成一个边长为9米的正方形.巩固练习 例4 某林场计划修一条长750m,断面为等腰梯形的渠道,断面面积为1.6m2,上口宽比渠深多2m,渠底比渠深多0.4m.
(1)渠道的上口宽与渠底宽各是多少?
(2)如果计划每天挖土48m3,需要多少天才能把这条渠道挖完?分析:因为渠深最小,为了便于计算,不妨设渠深为xm,则上口宽为x+2,渠底为x+0.4,那么,根据梯形的面积公式便可建模.学以致用解:(1)设渠深为xm 则渠底为(x+0.4)m,上口宽为(x+2)m依题意,得:整理,得:5x2+6x-8=0 解得:x1=0.8m,x2=-2(不合题意,舍去)∴上口宽为2.8m,渠底为1.2m.答:渠道的上口宽与渠底深各是2.8m和1.2m;
需要25天才能挖完渠道.学以致用1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为【 】
A.400cm2 B.500cm2 C.600cm2 D.4000cm2
2. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 】
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0AB巩固提高3.如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.巩固提高这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 列一元二次方程解应用题的步骤与
列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.课堂小结
2.平行四边形的面积公式是什么?
3.圆的面积公式是什么? 复习回顾 要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?分析:这本书的长宽之比是9:7,依题知正中央的矩形两边之比也为9:7解法一:设正中央的矩形两边分别为9xcm,7xcm
依题意得解得 故上下边衬的宽度为:
左右边衬的宽度为:探究新知分析:这本书的长宽之比是9:7,正中央的矩形两边之比也为9:7,由此判断上下边衬与左右边衬的宽度之比也为9:7解法二:设上下边衬的宽为9xcm,左右边衬宽为7xcm,依题意得解方程得(以下同学们自己完成)方程的哪个根合乎实际意义?为什么? 要设计一本书的封面,封面长27cm,宽21cm,正中央是一个与整个封面长宽比例相同的矩形,如果要使四周的边衬所占面积是封面面积的四分之一,上、下边衬等宽,左、右边衬等宽,应如何设计四周边衬的宽度?探究新知例1 (2004年,镇江)学校为了美化校园环境,在一块长40米、宽20米的长方形空地上计划新建一块长9米、宽7米的长方形花圃. 在学校计划新建的长方形花圃周长不变的情况下,长方形花圃的面积能否增加2平方米?如果能,请求出长方形花圃的长和宽;如果不能,请说明理由.学以致用解: 在长方形花圃周长不变的情况下,长方形花圃面积不能增加2平方米.由题意得长方形长与宽的和为16米.设长方形花圃的长为x米,则宽为(16-x)米.x(16-x)=63+2, x2-16x+65=0,∴此方程无解.∴在周长不变的情况下,长方形花圃的面积不能增加2平方米学以致用1、用20cm长的铁丝能否折成面积为30cm2的矩形,若能够,求它的长与宽;若不能,请说明理由.解:设这个矩形的长为xcm,则宽为 cm,即x2-10x+30=0这里a=1,b=-10,c=30,∴此方程无解.∴用20cm长的铁丝不能折成面积为30cm2的矩形.巩固练习例2 某校为了美化校园,准备在一块长32米,宽20米的长方形场地上修筑若干条道路,余下部分作草坪,并请全校同学参与设计,现在有两位学生各设计了一种方案(如图),根据两种设计方案各列出方程,求图中道路的宽分别是多少?使图(1),(2)的草坪面积为540m2.例题精讲解:(1)如图,设道路的宽为x米,则化简得,其中的 x=25超出了原矩形的宽,应舍去.∴图(1)中道路的宽为1米.例题精讲则横向的路面面积为 ,分析:此题的相等关系是矩形面积减去道路面积等于540m2。解法一、 如图,设道路的宽为x米,32x m2纵向的路面面积为 。20x m2注意:这两个面积的重叠部分是 x2m2?学以致用其中的 x=50超出了原矩形的长和宽,应舍去.
取x=2时,道路总面积为:答:所求道路的宽为2m。学以致用解法二:
我们利用“图形经过移动,它的面积大小不会改变”的道理,把纵、横两条路移动一下,使列方程容易些(目的是求出路面的宽,至于实际施工,仍可按原图的位置修路)学以致用横向路面 ,如图,设路宽为x米,32xm2纵向路面面积为 。20xm2草坪矩形的长(横向)为 ,草坪矩形的宽(纵向) 。相等关系是:草坪长×草坪宽=540m2(20-x)m(32-x)m再往下的计算、格式书写与解法1相同。学以致用2.如图是宽为20米,长为32米的矩形耕地,要修筑同样宽的三条道路(两条纵向,一条横向,且互相垂直),把耕地分成六块大小相等的试验地,要使试验地的面积为570平方米,问:道路宽为多少米?解:设道路宽为x米,则化简得,其中的 x=35超出了原矩形的宽,应舍去.答:道路的宽为1米.巩固练习3.如图,长方形ABCD,AB=15m,BC=20m,四周外围环绕着宽度相等的小路,已知小路的面积为246m2,求小路的宽度.解:设小路宽为x米,则化简得,答:小路的宽为3米.巩固练习例3 如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃。设花圃的宽AB为x米,面积为S平方米,
(1)求S与x的函数关系式;(2)如果要围成面积为45米2的花圃,AB的长是多少米?学以致用4.如图,用长为18m的篱笆(虚线部分),两面靠墙围成矩形的苗圃.要围成苗圃的面积为81m2,应该怎么设计?解:设苗圃的一边长为xm,则化简得,答:应围成一个边长为9米的正方形.巩固练习 例4 某林场计划修一条长750m,断面为等腰梯形的渠道,断面面积为1.6m2,上口宽比渠深多2m,渠底比渠深多0.4m.
(1)渠道的上口宽与渠底宽各是多少?
(2)如果计划每天挖土48m3,需要多少天才能把这条渠道挖完?分析:因为渠深最小,为了便于计算,不妨设渠深为xm,则上口宽为x+2,渠底为x+0.4,那么,根据梯形的面积公式便可建模.学以致用解:(1)设渠深为xm 则渠底为(x+0.4)m,上口宽为(x+2)m依题意,得:整理,得:5x2+6x-8=0 解得:x1=0.8m,x2=-2(不合题意,舍去)∴上口宽为2.8m,渠底为1.2m.答:渠道的上口宽与渠底深各是2.8m和1.2m;
需要25天才能挖完渠道.学以致用1.如图,宽为50cm的矩形图案由10个全等的小长方形拼成,则每个小长方形的面积为【 】
A.400cm2 B.500cm2 C.600cm2 D.4000cm2
2. 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整个挂图的面积是5400cm2,设金色纸边的宽为xcm,那么x满足的方程是【 】
A.x2+130x-1400=0 B.x2+65x-350=0
C.x2-130x-1400=0 D.x2-65x-350=0AB巩固提高3.如图,是长方形鸡场平面示意图,一边靠墙,另外三面用竹篱笆围成,若竹篱笆总长为35m,所围的面积为150m2,则此长方形鸡场的长、宽分别为_______.巩固提高这里要特别注意:在列一元二次方程解应用题时,由于所得的根一般有两个,所以要检验这两个根是否符合实际问题的要求. 列一元二次方程解应用题的步骤与
列一元一次方程解应用题的步骤类似,
即审、设、列、解、检、答.课堂小结
同课章节目录
