2016-2017学年高一数学人教B版必修1学案(学习导航 ):3.2.2对数函数-3.2.3指数函数与对数函数的关系
文档属性
| 名称 | 2016-2017学年高一数学人教B版必修1学案(学习导航 ):3.2.2对数函数-3.2.3指数函数与对数函数的关系 |
|
|
| 格式 | zip | ||
| 文件大小 | 189.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 00:00:00 | ||
图片预览



文档简介
3.2.2
对数函数-3.2.3
指数函数与对数函数的关系
自主整理
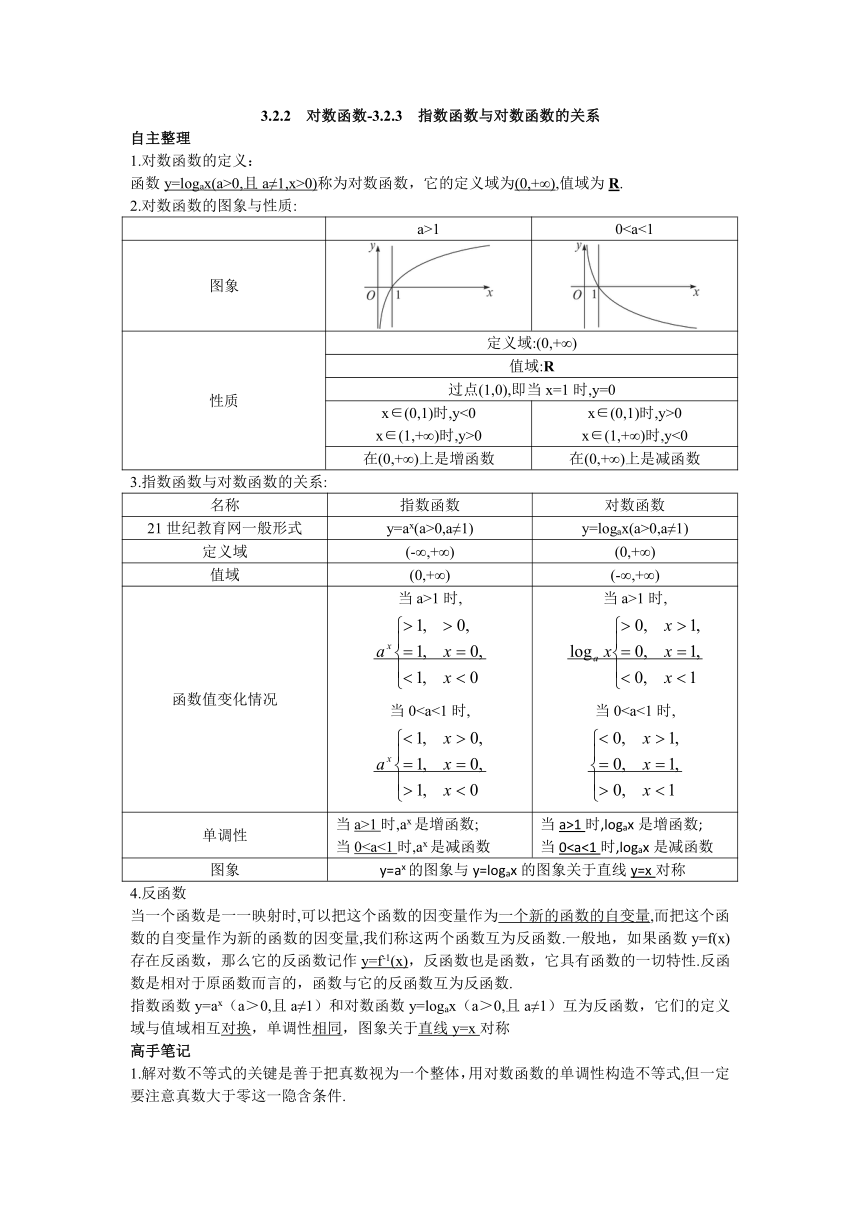
1.对数函数的定义:
函数y=logax(a>0,且a≠1,x>0)称为对数函数,它的定义域为(0,+∞),值域为R.
2.对数函数的图象与性质:
a>1
0图象
性质
定义域:(0,+∞)
值域:R
过点(1,0),即当x=1时,y=0
x∈(0,1)时,y<0x∈(1,+∞)时,y>0
x∈(0,1)时,y>0x∈(1,+∞)时,y<0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
3.指数函数与对数函数的关系:
名称
指数函数
对数函数
21世纪教育网一般形式
y=ax(a>0,a≠1)
y=logax(a>0,a≠1)
定义域
(-∞,+∞)
(0,+∞)
值域
(0,+∞)
(-∞,+∞)
函数值变化情况
当a>1时,当0当a>1时,当0单调性
当a>1时,ax是增函数;当0当a>1时,logax是增函数;当0图象
y=ax的图象与y=logax的图象关于直线y=x对称
4.反函数
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数.一般地,如果函数y=f(x)存在反函数,那么它的反函数记作y=f-1(x),反函数也是函数,它具有函数的一切特性.反函数是相对于原函数而言的,函数与它的反函数互为反函数.
指数函数y=ax(a>0,且a≠1)和对数函数y=logax(a>0,且a≠1)互为反函数,它们的定义域与值域相互对换,单调性相同,图象关于直线y=x对称
高手笔记
1.解对数不等式的关键是善于把真数视为一个整体,用对数函数的单调性构造不等式,但一定要注意真数大于零这一隐含条件.
2.求函数定义域时,常见的限制条件有:分母不为零,开偶次方时被开方数非负,对数的真数大于零,底数大于零且不等于1等.
3.考查对数函数与其他函数组成的复合函数时,要注意利用复合函数的单调性法则和函数单调性的定义.考查对数函数的值域问题时,要注意只有当对数的真数取到所有的正数时,对数值才可能取到所有的实数.
4.利用对数函数的图象的平移和对称可以认识与对数函数有关的一些函数的图象和性质,这些图象的变换规律与指数函数的有关图象变换规律是类似的.
5.作出函数y=logax的图象,再将所得图象沿y轴对称到y轴左侧,所得两部分组合在一起就是函数y=loga|x|的图象.作出函数y=logax的图象,再将所得图象在x轴下方的部分沿x轴翻折到x轴上方,与原x轴上方的部分一起,就是y=|logax|的图象.
名师解惑
1.比较两个对数的大小,一般可采用哪些方法?
剖析:两数(式)大小的比较主要是找出适当的函数,把要比较的两数作为此函数的函数值,然后利用函数的单调性等来比较两数的大小.一般采用的方法有:
(1)直接法:由函数的单调性直接作答;
(2)作差法:把两数作差变形,然后判断其大于、等于、小于零来确定;
(3)作商法:若两数同号,把两数作商变形,判断其大于、等于、小于1来确定;
(4)转化法:把要比较的两数适当地转化成两个新数大小的比较;
(5)媒介法:选取适当的“媒介”数,分别与要比较的两数比较大小,从而间接地求得两数的大小.
2.对数函数的图象特征和对数函数的性质之间有哪些对应关系?
剖析:对数函数的图象特征和对数函数的性质之间有以下对应关系:
(1)图象都位于y轴右侧,且以y轴为渐近线→函数定义域为(0,+∞).
(2)图象向上、向下无限延展→函数值域为R.
(3)图象恒过定点(1,0)→1的对数是零,即loga1=0.
(4)当a>1时,图象由左向右逐渐上升→当a>1时,y=logax在(0,+∞)上是增函数;
当0<a<1时,图象由左向右逐渐下降→当0<a<1时,y=logax在(0,+∞)上是减函数.(5)当a>1时,在直线x=1的右侧,图象位于x轴上方;在直线x=1与y轴之间,图象位于x轴下方→当a>1时,x>1,则y=logax>0;0<x<1,则y=logax<0.
当0<a<1时,在直线x=1的右侧,图象位于x轴下方;在直线x=1与y轴之间,图象位于x轴上方→当0<a<1时,x>1,则y=logax<0;0<x<1,则y=logax>0.
3.怎样把对数函数与指数函数联系起来研究
剖析:(1)对数函数的反函数是指数函数,所以要利用指数函数的性质来研究对数函数.应该注意到:这两种函数都要求底数a>0,且a≠1;对数函数的定义域为(0,+∞),结合图象看,对数函数在y轴左侧没有图象,即负数与0没有对数,也就是真数必须大于0.这些知识可以用来求含有对数函数的定义域.
(2)通过将对数函数与指数函数的图象进行对比,可以发现:当a>1,或0<a<1时,对数函数与指数函数的单调性是一致的〔即在区间(0,+∞)上同时为增函数,或者同时为减函数〕.对数函数的图象都经过点(1,0),这与性质loga1=0?a0=1是分不开的.(3)既然对数函数y=logax与指数函数y=ax互为反函数,那么它们的图象关于直线y=x对称.于是通过对a分情况(约定不同的取值范围),再结合函数y=log2x,y=logx的图象来揭示对数函数的性质,应该是一件水到渠成的事.
讲练互动
图3-2-2
【例题1】图3-2-2是对数函数y=logax当底数a的值分别取,,,时所对应图象,则相应于C1,C2,C3,C4的a的值依次是(
)
A.,,,
B.,,,
C.,,,
D.,,,
解析:因为底数a大于1时,对数函数的图象自左向右呈上升趋势,且a越大,图象就越靠近x轴;底数a大于0且小于1时,对数函数的图象自左向右呈下降趋势,且a越小,图象就越靠近x轴.
答案:A
绿色通道
由对数函数的图象间的相对位置关系判断底数a的相互关系,应根据对数函数图象与底数间的变化规律来处理.在指数函数y=ax中,底数a越接近1,相应的图象就越接近直线y=1,对数函数与指数函数是一对反函数,其图象是关于直线y=x对称的,直线y=1关于直线y=x的对称直线是x=1,所以我们有结论:对数函数y=logax,底数a越接近1,其图象就越接近直线x=1.
变式训练
1.若loga2)
A.0B.0C.a>b>1
D.b>a>1
解析:注意到此题两对数值底数不同真数相同,用图象法或用换底公式均可.
方法一:由底数与对数函数的图象关系(如图)可知y=logax,y=logbx图象的大致走向.
再由对数函数的图象规律:从第一象限看,自左向右底数依次增大.
方法二:利用换底公式转化成同底的对数再进行比较.
由已知,得<0,则0>log2a>log2b,即log21>log2a>log2b.
∵y=log2x为增函数,
∴0方法三:取特殊值法.
∵log2=-1,log2=,
∴log2∴可取a=,b=,则0答案:B
【例题2】比较大小:
(1)log0.27与log0.29;
(2)log35与log65;
(3)(lgm)1.9与(lgm)2.1(m>1);
(4)log85与lg4.
分析:(1)log0.27和log0.29可看作是函数y=log0.2x,当x=7和x=9时对应的两函数值,由y=log0.2x在(0,+∞)上单调递减,得log0.27>log0.29.
(2)考查函数y=logax底数a>1的底数变化规律,函数y=log3x(x>1)的图象在函数y=log6x(x>1)的上方,故log35>log65.
(3)把lgm看作指数函数的底数,要比较两数的大小,关键是比较底数lgm与1的关系.若lgm>1即m>10,则(lgm)x在R上单调递增,故(lgm)1.9<(lgm)2.1;若0<lgm<1即1<m<10,则(lgm)x在R上单调递减,故(lgm)1.9>(lgm)2.1;若lgm=1即m=10,则(lgm)1.9=(lgm)2.1.
(4)因为底数8、10均大于1,且10>8,
所以log85>lg5>lg4,即log85>lg4.
解:(1)log0.27>log0.29.
(2)log35>log65.
(3)当m>10时,(lgm)1.9<(lgm)2.1;当m=10时,
(lgm)1.9=(lgm)2.1;当1<m<10时,(lgm)1.9>(lgm)2.1.
(4)log85>lg4.
绿色通道本题比较大小代表了几个典型的题型.其中题(1)是直接利用对数函数的单调性;题(2)是对数函数底数变化规律的应用;题(3)是指数函数单调性及对数函数性质的综合运用;题(4)是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的增减性.常用的中间量有0、1、2等可通过估算加以选择.变式训练
2.比较下列各组数中两个值的大小:
(1)log23.4,log28.5;
(2)log0.31.8;log0.32.7;
(3)loga5.1,loga5.9(a>0且a≠1);
(4)log67,log76.
分析:对于底数相同的两个对数值比较大小,可由对数的单调性确定,利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较两个数的大小.
解:(1)考查对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4log0.32.7.
(3)对数函数的增减性决定于对数的底数是大于1还是小于1,而已知条件中并未明确指出底数a与1哪个大,因此需要对底数a进行讨论:
当a>1时,函数y=logax在(0,+∞)上是增函数,于是loga5.1当0loga5.9.
(4)∵log67>log66=1,log76∴log67>log76.
【例题3】已知函数y=lg(-x),求其定义域,并判断其奇偶性、单调性.
分析:注意到+x=,即有lg(-x)=-lg(+x),从而f(-x)=lg(+x)=-lg(-x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
解:由题意-x>0,解得x∈R,即定义域为R.
又f(-x)=lg[-(-x)]
=lg(+x)=lg
=lg(-x)-1=-lg(-x)
=-f(x),
∴y=lg(-x)是奇函数.
任取x1、x2∈(0,+∞),且x1<x2,
则>,
即有-x1>-x2>0,
∴lg(-x1)>lg(-x2),
即f(x1)>f(x2)成立.
∴f(x)在(0,+∞)上为减函数.
又f(x)是定义在R上的奇函数,
故f(x)在(-∞,0)上也为减函数.
绿色通道研究函数的性质一定得先考虑定义域.在研究函数单调性时,注意奇偶性对函数单调性的影响,即偶函数在关于原点对称的区间上具有相反的单调性,奇函数在关于原点对称的区间上具有相同的单调性.
变式训练
3.(2006广东高考,1)函数f(x)=+lg(3x+1)的定义域是(
)
A.(,+∞)
B.(,1)
C.(,)
D.(-∞,)
解析:由
答案:B
【例题4】(1)解不等式:log3(4-x)>2+log3x;
(2)解方程:-3lgx+4=0.
分析:对于(1),将对数不等式转化为解代数不等式组,对于(2)用换元法将其转化为一元二次方程.
解:(1)原不等式可化为log3(4-x)>log3(9x),
其等价于
解得0∴原不等式的解集为{x|0(2)设=t,则t≥0.
原方程化为-t2+t+2=0.
解得t=2,或t=-1(舍去).
由=2,得lgx=2.故x=100.
经检验x=100是原方程的解.
黑色陷阱(1)形如f(logax)=0,f(logax)>0的对数方程或不等式,往往令t=logax进行换元转化.
(2)解对数方程和不等式时要注意防止定义域的扩大,处理办法为:第一,若不是同解变形,最后一定要验根;第二,解的过程中要加以限制条件,使定义域保持不变,即进行同解变形,最后通过解混合不等式组得到原不等式的解.
变式训练
4.(2006陕西高考,理4)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),则a+b等于(
)
A.3
B.4
C.5
D.6
解析:因为函数f(x)的图象经过点(2,1),所以f(2)=1,即loga(2+b)=1,即a=2+b.
又其反函数的图象经过点(2,8),故函数f(x)的图象经过点(8,2),有loga(8+b)=2,即a2=8+b,解得a=-2,b=-4(舍去),或a=3,b=1,所以a+b=4.
答案:B
5.设函数f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1),则f(log2x)的最小值为_____________.
解析:由已知,得
即
由①得log2a=1,∴a=2.
代入②得b=2.∴f(x)=x2-x+2.
∴f(log2x)=log22x-log2x+2=(log2x)2+.
∴当log2x=时,f(log2x)取得最小值,此时x=.
答案:
对数函数-3.2.3
指数函数与对数函数的关系
自主整理
1.对数函数的定义:
函数y=logax(a>0,且a≠1,x>0)称为对数函数,它的定义域为(0,+∞),值域为R.
2.对数函数的图象与性质:
a>1
0
性质
定义域:(0,+∞)
值域:R
过点(1,0),即当x=1时,y=0
x∈(0,1)时,y<0x∈(1,+∞)时,y>0
x∈(0,1)时,y>0x∈(1,+∞)时,y<0
在(0,+∞)上是增函数
在(0,+∞)上是减函数
3.指数函数与对数函数的关系:
名称
指数函数
对数函数
21世纪教育网一般形式
y=ax(a>0,a≠1)
y=logax(a>0,a≠1)
定义域
(-∞,+∞)
(0,+∞)
值域
(0,+∞)
(-∞,+∞)
函数值变化情况
当a>1时,当0
当a>1时,ax是增函数;当0
y=ax的图象与y=logax的图象关于直线y=x对称
4.反函数
当一个函数是一一映射时,可以把这个函数的因变量作为一个新的函数的自变量,而把这个函数的自变量作为新的函数的因变量,我们称这两个函数互为反函数.一般地,如果函数y=f(x)存在反函数,那么它的反函数记作y=f-1(x),反函数也是函数,它具有函数的一切特性.反函数是相对于原函数而言的,函数与它的反函数互为反函数.
指数函数y=ax(a>0,且a≠1)和对数函数y=logax(a>0,且a≠1)互为反函数,它们的定义域与值域相互对换,单调性相同,图象关于直线y=x对称
高手笔记
1.解对数不等式的关键是善于把真数视为一个整体,用对数函数的单调性构造不等式,但一定要注意真数大于零这一隐含条件.
2.求函数定义域时,常见的限制条件有:分母不为零,开偶次方时被开方数非负,对数的真数大于零,底数大于零且不等于1等.
3.考查对数函数与其他函数组成的复合函数时,要注意利用复合函数的单调性法则和函数单调性的定义.考查对数函数的值域问题时,要注意只有当对数的真数取到所有的正数时,对数值才可能取到所有的实数.
4.利用对数函数的图象的平移和对称可以认识与对数函数有关的一些函数的图象和性质,这些图象的变换规律与指数函数的有关图象变换规律是类似的.
5.作出函数y=logax的图象,再将所得图象沿y轴对称到y轴左侧,所得两部分组合在一起就是函数y=loga|x|的图象.作出函数y=logax的图象,再将所得图象在x轴下方的部分沿x轴翻折到x轴上方,与原x轴上方的部分一起,就是y=|logax|的图象.
名师解惑
1.比较两个对数的大小,一般可采用哪些方法?
剖析:两数(式)大小的比较主要是找出适当的函数,把要比较的两数作为此函数的函数值,然后利用函数的单调性等来比较两数的大小.一般采用的方法有:
(1)直接法:由函数的单调性直接作答;
(2)作差法:把两数作差变形,然后判断其大于、等于、小于零来确定;
(3)作商法:若两数同号,把两数作商变形,判断其大于、等于、小于1来确定;
(4)转化法:把要比较的两数适当地转化成两个新数大小的比较;
(5)媒介法:选取适当的“媒介”数,分别与要比较的两数比较大小,从而间接地求得两数的大小.
2.对数函数的图象特征和对数函数的性质之间有哪些对应关系?
剖析:对数函数的图象特征和对数函数的性质之间有以下对应关系:
(1)图象都位于y轴右侧,且以y轴为渐近线→函数定义域为(0,+∞).
(2)图象向上、向下无限延展→函数值域为R.
(3)图象恒过定点(1,0)→1的对数是零,即loga1=0.
(4)当a>1时,图象由左向右逐渐上升→当a>1时,y=logax在(0,+∞)上是增函数;
当0<a<1时,图象由左向右逐渐下降→当0<a<1时,y=logax在(0,+∞)上是减函数.(5)当a>1时,在直线x=1的右侧,图象位于x轴上方;在直线x=1与y轴之间,图象位于x轴下方→当a>1时,x>1,则y=logax>0;0<x<1,则y=logax<0.
当0<a<1时,在直线x=1的右侧,图象位于x轴下方;在直线x=1与y轴之间,图象位于x轴上方→当0<a<1时,x>1,则y=logax<0;0<x<1,则y=logax>0.
3.怎样把对数函数与指数函数联系起来研究
剖析:(1)对数函数的反函数是指数函数,所以要利用指数函数的性质来研究对数函数.应该注意到:这两种函数都要求底数a>0,且a≠1;对数函数的定义域为(0,+∞),结合图象看,对数函数在y轴左侧没有图象,即负数与0没有对数,也就是真数必须大于0.这些知识可以用来求含有对数函数的定义域.
(2)通过将对数函数与指数函数的图象进行对比,可以发现:当a>1,或0<a<1时,对数函数与指数函数的单调性是一致的〔即在区间(0,+∞)上同时为增函数,或者同时为减函数〕.对数函数的图象都经过点(1,0),这与性质loga1=0?a0=1是分不开的.(3)既然对数函数y=logax与指数函数y=ax互为反函数,那么它们的图象关于直线y=x对称.于是通过对a分情况(约定不同的取值范围),再结合函数y=log2x,y=logx的图象来揭示对数函数的性质,应该是一件水到渠成的事.
讲练互动
图3-2-2
【例题1】图3-2-2是对数函数y=logax当底数a的值分别取,,,时所对应图象,则相应于C1,C2,C3,C4的a的值依次是(
)
A.,,,
B.,,,
C.,,,
D.,,,
解析:因为底数a大于1时,对数函数的图象自左向右呈上升趋势,且a越大,图象就越靠近x轴;底数a大于0且小于1时,对数函数的图象自左向右呈下降趋势,且a越小,图象就越靠近x轴.
答案:A
绿色通道
由对数函数的图象间的相对位置关系判断底数a的相互关系,应根据对数函数图象与底数间的变化规律来处理.在指数函数y=ax中,底数a越接近1,相应的图象就越接近直线y=1,对数函数与指数函数是一对反函数,其图象是关于直线y=x对称的,直线y=1关于直线y=x的对称直线是x=1,所以我们有结论:对数函数y=logax,底数a越接近1,其图象就越接近直线x=1.
变式训练
1.若loga2
A.0
D.b>a>1
解析:注意到此题两对数值底数不同真数相同,用图象法或用换底公式均可.
方法一:由底数与对数函数的图象关系(如图)可知y=logax,y=logbx图象的大致走向.
再由对数函数的图象规律:从第一象限看,自左向右底数依次增大.
方法二:利用换底公式转化成同底的对数再进行比较.
由已知,得<0,则0>log2a>log2b,即log21>log2a>log2b.
∵y=log2x为增函数,
∴0
∵log2=-1,log2=,
∴log2
【例题2】比较大小:
(1)log0.27与log0.29;
(2)log35与log65;
(3)(lgm)1.9与(lgm)2.1(m>1);
(4)log85与lg4.
分析:(1)log0.27和log0.29可看作是函数y=log0.2x,当x=7和x=9时对应的两函数值,由y=log0.2x在(0,+∞)上单调递减,得log0.27>log0.29.
(2)考查函数y=logax底数a>1的底数变化规律,函数y=log3x(x>1)的图象在函数y=log6x(x>1)的上方,故log35>log65.
(3)把lgm看作指数函数的底数,要比较两数的大小,关键是比较底数lgm与1的关系.若lgm>1即m>10,则(lgm)x在R上单调递增,故(lgm)1.9<(lgm)2.1;若0<lgm<1即1<m<10,则(lgm)x在R上单调递减,故(lgm)1.9>(lgm)2.1;若lgm=1即m=10,则(lgm)1.9=(lgm)2.1.
(4)因为底数8、10均大于1,且10>8,
所以log85>lg5>lg4,即log85>lg4.
解:(1)log0.27>log0.29.
(2)log35>log65.
(3)当m>10时,(lgm)1.9<(lgm)2.1;当m=10时,
(lgm)1.9=(lgm)2.1;当1<m<10时,(lgm)1.9>(lgm)2.1.
(4)log85>lg4.
绿色通道本题比较大小代表了几个典型的题型.其中题(1)是直接利用对数函数的单调性;题(2)是对数函数底数变化规律的应用;题(3)是指数函数单调性及对数函数性质的综合运用;题(4)是中间量的运用.当两个对数的底数和真数都不相同时,需要找出中间量来“搭桥”,再利用对数函数的增减性.常用的中间量有0、1、2等可通过估算加以选择.变式训练
2.比较下列各组数中两个值的大小:
(1)log23.4,log28.5;
(2)log0.31.8;log0.32.7;
(3)loga5.1,loga5.9(a>0且a≠1);
(4)log67,log76.
分析:对于底数相同的两个对数值比较大小,可由对数的单调性确定,利用对数函数的增减性比较两个对数的大小.当不能直接进行比较时,可在两个对数中间插入一个已知数(如1或0等),间接比较两个数的大小.
解:(1)考查对数函数y=log2x,因为它的底数2>1,所以它在(0,+∞)上是增函数,于是log23.4
(3)对数函数的增减性决定于对数的底数是大于1还是小于1,而已知条件中并未明确指出底数a与1哪个大,因此需要对底数a进行讨论:
当a>1时,函数y=logax在(0,+∞)上是增函数,于是loga5.1
(4)∵log67>log66=1,log76
【例题3】已知函数y=lg(-x),求其定义域,并判断其奇偶性、单调性.
分析:注意到+x=,即有lg(-x)=-lg(+x),从而f(-x)=lg(+x)=-lg(-x)=-f(x),可知其为奇函数.又因为奇函数在关于原点对称的区间上的单调性相同,所以我们只需研究(0,+∞)上的单调性.
解:由题意-x>0,解得x∈R,即定义域为R.
又f(-x)=lg[-(-x)]
=lg(+x)=lg
=lg(-x)-1=-lg(-x)
=-f(x),
∴y=lg(-x)是奇函数.
任取x1、x2∈(0,+∞),且x1<x2,
则>,
即有-x1>-x2>0,
∴lg(-x1)>lg(-x2),
即f(x1)>f(x2)成立.
∴f(x)在(0,+∞)上为减函数.
又f(x)是定义在R上的奇函数,
故f(x)在(-∞,0)上也为减函数.
绿色通道研究函数的性质一定得先考虑定义域.在研究函数单调性时,注意奇偶性对函数单调性的影响,即偶函数在关于原点对称的区间上具有相反的单调性,奇函数在关于原点对称的区间上具有相同的单调性.
变式训练
3.(2006广东高考,1)函数f(x)=+lg(3x+1)的定义域是(
)
A.(,+∞)
B.(,1)
C.(,)
D.(-∞,)
解析:由
答案:B
【例题4】(1)解不等式:log3(4-x)>2+log3x;
(2)解方程:-3lgx+4=0.
分析:对于(1),将对数不等式转化为解代数不等式组,对于(2)用换元法将其转化为一元二次方程.
解:(1)原不等式可化为log3(4-x)>log3(9x),
其等价于
解得0
原方程化为-t2+t+2=0.
解得t=2,或t=-1(舍去).
由=2,得lgx=2.故x=100.
经检验x=100是原方程的解.
黑色陷阱(1)形如f(logax)=0,f(logax)>0的对数方程或不等式,往往令t=logax进行换元转化.
(2)解对数方程和不等式时要注意防止定义域的扩大,处理办法为:第一,若不是同解变形,最后一定要验根;第二,解的过程中要加以限制条件,使定义域保持不变,即进行同解变形,最后通过解混合不等式组得到原不等式的解.
变式训练
4.(2006陕西高考,理4)设函数f(x)=loga(x+b)(a>0,a≠1)的图象过点(2,1),其反函数的图象过点(2,8),则a+b等于(
)
A.3
B.4
C.5
D.6
解析:因为函数f(x)的图象经过点(2,1),所以f(2)=1,即loga(2+b)=1,即a=2+b.
又其反函数的图象经过点(2,8),故函数f(x)的图象经过点(8,2),有loga(8+b)=2,即a2=8+b,解得a=-2,b=-4(舍去),或a=3,b=1,所以a+b=4.
答案:B
5.设函数f(x)=x2-x+b,且f(log2a)=b,log2[f(a)]=2(a≠1),则f(log2x)的最小值为_____________.
解析:由已知,得
即
由①得log2a=1,∴a=2.
代入②得b=2.∴f(x)=x2-x+2.
∴f(log2x)=log22x-log2x+2=(log2x)2+.
∴当log2x=时,f(log2x)取得最小值,此时x=.
答案:
