辽宁省凌海市七年级数学下册课后补习班辅导期末复习—有理数、代数式及其运算讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导期末复习—有理数、代数式及其运算讲学案苏科版 |
|
|
| 格式 | zip | ||
| 文件大小 | 209.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 00:00:00 | ||
图片预览





文档简介
期末复习—有理数、代数式及其运算
【本讲教育信息】
一. 教学内容:
期末复习——有理数、代数式及其运算
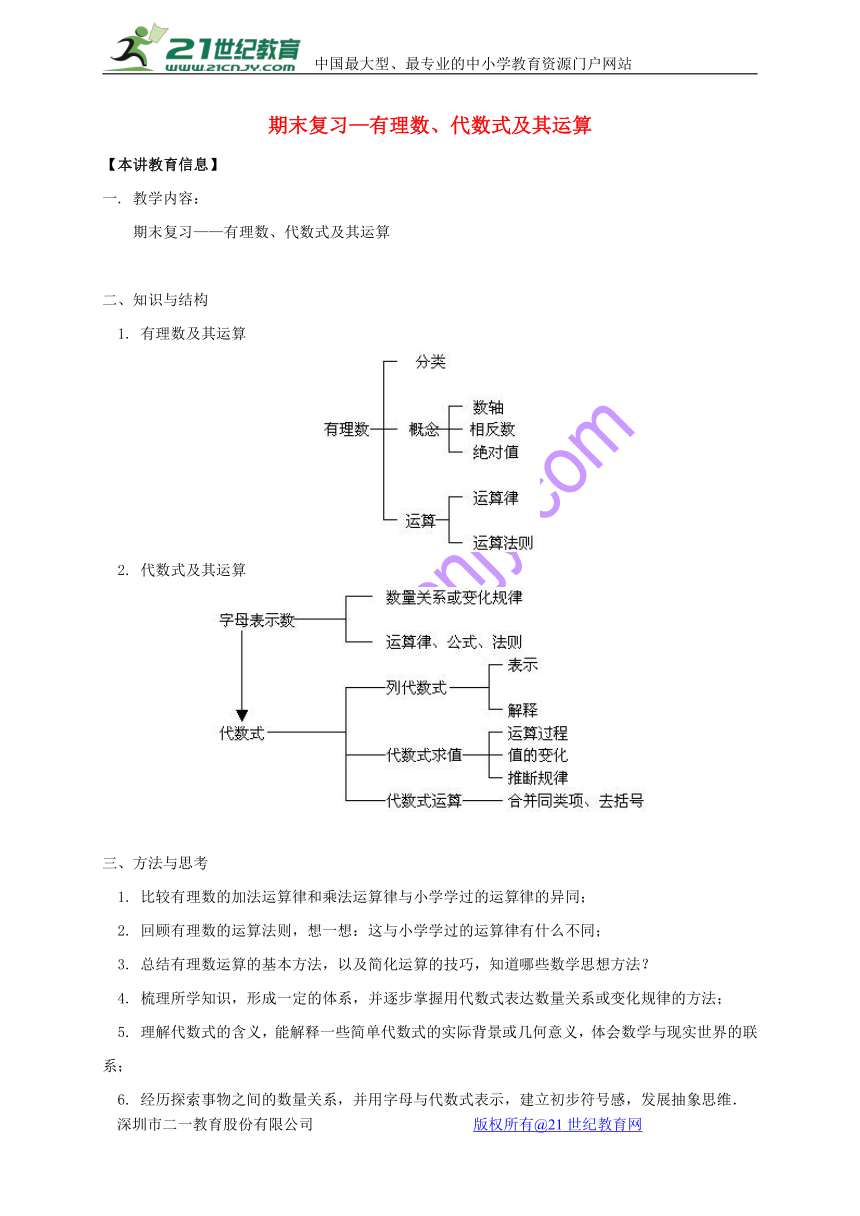
二、知识与结构
1. 有理数及其运算
2. 代数式及其运算
三、方法与思考
1. 比较有理数的加法运算律和乘法运算律与小学学过的运算律的异同;
2. 回顾有理数的运算法则,想一想:这与小学学过的运算律有什么不同;
3. 总结有理数运算的基本方法,以及简化运算的技巧,知道哪些数学思想方法?
4. 梳理所学知识,形成一定的体系,并逐步掌握用代数式表达数量关系或变化规律的方法;
5. 理解代数式的含义,能解释一些简单代数式的实际背景或几何意义,体会数学与现实世界的联系;
6. 经历探索事物之间的数量关系,并用字母与代数式表示,建立初步符号感,发展抽象思维.
四、错题回放
1. 代数式书写规范.如a的倍写成a ,应为.
2. 代数式描述语句顺序不理解.如a,b两数的平方和写成,应为.
3. 合并同类项中出错.如,.
4. 去括号中符号出错.如,.
5. 探索规律出错.如由1+3=4=22, 1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,… 猜想1+3+5+7+…+(2n+1)=n2 (n为正整数)21世纪教育网版权所有
【典型例题】
例1. 如图,在数轴上有三个点A、B、C,回答下列问题:
(1)将B点向右移动6个单位,三个点中哪个点所表示的数最小?
(2)将C点向左移动6个单位,三个点中哪个点所表示的数最小?
(3)怎样移动A、B、C中两个点,才能使三个点所表示的数相同?有几种移动方法?
分析:注意移动的方向及相关点所对应的有理数.
解:(1)B点向右移动6个单位就为-1+6=5,所以三个点中A点-2最小;
(2)C点向左移动6个单位就为2-6=-4,所以三个点中C点-4最小;
(3)有三种方法:
①将B点向左移动1个单位;将C点向左移动4个单位;则三个数都为-2
②将A点向右移动1个单位;将C点向左移动3个单位;则三个数都为-1
③将A点向右移动4个单位;将B点向右移动3个单位;则三个数都为2
例2. 有理数a、b、c在数轴上的位置如图所示,其中O是原点,=.
(1)用“<”把a、b、-a、-b连接起来;
(2)b+c的值是多少?
(3)判断a+b与a+c的符号.
分析:比较a、b、-a、-b的大小时,可根据互为相反数的两个数在原点两侧,并且到原点的距离相等这一原理,在数轴上画出表示-a、-b的两点,即可得它们的大小关系.
解:(1)a< b< -b <-a
(2)b+c=0
(3)a+b< 0为“-”; a+c< 0也为“-”
说明:此题也可结合数轴,让问题“具体化”,如取a、b、c的值,算出-a、-b的值,把它们大小比较出来后再“一般化”.21教育网
例3. 计算:
(1);
(2).
分析:(1)对要注意与的区别,许多同学会混淆;
(2)对有理数的混合运算,应先乘方再乘除后加减,如果有括号,还应先进行括号里的运算.第(2)题中每个加数都有,因此可以逆用分配律进行计算.www.21-cn-jy.com
解:(1)原式=
=
=
=
(2)原式=
=
=
例4. 某医院急诊病房收治了一位病人,每隔2时测得该病人的体温如下表(单位:℃)(正常人的体温是37℃)2·1·c·n·j·y
(1)这位病人在这一天8时到18时之间,哪个时刻的体温最高?哪个时刻的体温最低?
(2)该病人这一天的平均体温是多少摄氏度?
(3)以正常体温37℃为原点,用折线图表示该病人体温的变化情况.
时刻
8时
10时
12时
14时
16时
18时
体温
38.5
38.8
39.5
39.6
38
37.5
与正常人的正
常体温的差值
+1.5
+1.8
+2.5
+2.6
+1
+0.5
解:
(1)14时的体温最高;18时的体温最低
(2)[(+1.5)+(+1.8)+(+2.5)+(+2.6)+(+1)+(+0.5)]÷6=1.65
37+1.65=38.65
(3)图略(描点连线)
例5. 3个球队进行单循环比赛(参赛的每个队都与其他队赛一场),总的比赛场数是多少?4个球队呢?写出m个球队进行单循环比赛时总的比赛场数n的公式.【来源:21·世纪·教育·网】
解:3个球队进行单循环比赛要赛3场;
4个球队进行单循环比赛要赛6场;
m个球队进行单循环比赛要赛n=场;
说明:每一个球队都可以有(m-1)场比赛,一共有m个球队,所以有m(m-1)场比赛,但由于是单循环,所以每两个球队只需要赛一场。因此总场数为场。www-2-1-cnjy-com
例6. 先化简,再求值: ,其中.
解:原式=
=
=
当时,上式===
例7. 有若干个数,第1个数记为,第2个数记为,第3个数记为,…,第n个数记为,若,从第2个数起,每一个数都等于“1与它前面的那个数的差的倒数”则① ,= , ;②根据以上结果可知: , .
解:①
=
②根据以上结果可知:3,
说明:由、、、可知,每3个数一个循环,也就是、和3这3个数循环出现。因此我们用1998÷3余0知,应为末尾的3;而1999÷3余1知,则应为第一个数。
【模拟试题】(答题时间:90分钟)
一、选择题:
1. 的相反数是 ( )
A. -2 B. 2 C. D.
2. 如果一个数的平方等于它的倒数,那么这个数一定是 ( )
A. 0 B. 1 C. -1 D. 1或-1
3. 如果两个有理数的和是负数,那么这两个数 ( )
A. 一定都是负数 B. 至少有一个是负数
C. 一定都是非正数 D. 一定是一个正数和一个负数
4. 下列结论中,不正确的是 ( )
A. 1除以非零数的商,叫做这个数的倒数
B. 两个数的积为1,这两个数互为倒数
C. 一个数的倒数一定小于这个数
D. 一个数和它的倒数的商等于这个数的平方
5. 有下列各数,0.01,10,-6.67,,0,-90,-(-3),,,其中属于非负整数的共有 ( )【出处:21教育名师】
A. 1个 B. 2个 C. 3个 D. 4个
6. 下图所示是一个数值转换机,输入x,输出3(x-1),下面给出了四种转换步骤,其中不正确的是 ( )【版权所有:21教育】
A. 先减去1,再乘以3
B. 先乘以3,再减去1
C. 先乘以3,再减去3
D. 先加上-1,再乘以3
7. 下列各组代数式中,不是同类项的是 ( )
A. B. C. D.
8. 如图用火柴棒搭正方形,甲、乙、丙、丁四位同学都用x表示所搭正方形的个数,从而计算火柴棒的根数,他们计算的结果分别是: ( )21教育名师原创作品
甲:4+3(x-1);乙:x+x+(x+1);丙:1+3x;丁:4x-(x-1).
其中计算结果正确的同学有 ( )
A. 1位 B. 2位 C. 3位 D. 4位
二、填空题:
9. 的大小关系: .
10. 绝对值小于4的负整数有 个,正整数有 个,整数有 个.
11. 水池中的水位在某天八个不同时刻测得记录如下(规定上升为正,单位:厘米):
+3,-6,-1,+5,-4,+2,-2,-3,那么这天中水池水位最终的变化情况是 .
12. 数轴上,与表示-2的点的距离为3的数是 .
13. 初一(3)班要添置新桌椅,使每人一套桌椅,其中有x行每行7人,另外还有两行8人,则共需 套桌椅,当x=4时,共需 套桌椅.21*cnjy*com
14. 当m= ,n= 时,和是同类项.
15. 若=7,则= .
16. 已知,,则 , .
17. 列代数式表示
①长方形的周长为20cm,它的宽为xcm,那么它的面积为 ;
②某商品的利润为a元,利润率为10%,此商品进价为 ;
③甲乙两地相距x千米,某人原计划t小时到达,后因故提前1小时到达,则他每小时应比原计划多走 千米;21·cn·jy·com
④托运行李p千克(p为整数)的费用标准:已知托运第1个1千克需付2元,以后每增加1千克(不足1千克按1千克计)需增加费用5角.若某人托运p千克(p>1)的行李,则托运费用为 ;
⑤一个两位数,它的十位数字为x,个位数字比十位数字大3,则这个两位数为
三、计算与化简:
18. ;
19. ;
20. ;
21. .
22. 化简:
① ②
23. 先化简,再求值:
①,其中
②,其中,
四、辨析与思考:
24. ①.
辨析:
②=.
辨析:
五、操作与解释:
25. 某食品厂从生产的食品罐头中,抽出样品20听检查每听的质量,超过和不足标准的部分分别用正、负数表示,记录如下:21cnjy.com
与标准质量的偏差/克
-10
-5
0
+5
+10
+15
听数
1
2
4
7
5
1
问:这批样品平均每听质量比标准每听质量多或少几克?
y(℃)
25
25+2.5
25+5
25+7.5
25+10
…
x(次/分)
20
30
40
50
60
…
26. 生物学家发现,气温y在一定温度内时,某种蟋蟀每分钟鸣叫的次数x与气温y(单位:℃)有一定的关系,下表是通过实验得到的一组数据:21·世纪*教育网
(1)根据表中的数据,写出y与x之间的关系式
(2)当这种蟋蟀每分钟鸣叫56次时,该地当时的气温多少?
27. 小王和小张在玩“24”点游戏,他们互相给对方四张牌,要求对方根据牌上的数字凑成“24”点,他们互给对方的牌上的数字如下:①黑桃1,方块2,红桃2,黑桃3;②方块1,草花3,草花7和红桃12. 请你帮他们凑成“24”点.2-1-c-n-j-y
28. 如图,按一定的规律用牙签搭图形:
(1)按图示的规律填表:
图形标号
①
②
③
……
⑩
牙签根数
……
(2)搭第n个图形需要________________________根牙签.
六、探索与思考:
29. 先观察==1-=
==1-=
再计算的值
30. 你能比较两个数的大小吗?
为了解决这个问题,我们首先把它们抽象成一般形式,即比较的大小(n为自然数),我们从分析特殊向简单的情形入手,令n=1,n=2,n=3,…对其进行分析,从中发现规律,经过归纳,猜想出结论.21*cnjy*com
(1)计算,比较下列各组数中两个数的大小在空格中填“>”、“=”、“<”
, , , , ,…
(2)从上面的结果进行归纳猜想,的大小关系是 .
(3)根据上面的归纳猜想出一般结论,试比较的大小.
【试题答案】
1. D 2. B 3. B 4. C 5. D 6. B 7. C 8. D 【来源:21cnj*y.co*m】
9. > 10. 3;3;7 11. 下降了6个单位 12. -5或1
13. 7x+16;44 14. m=4,n=1 15. 4 16. 4,12
17. ①x(10-x) ②元 ③()千米
④[2+0.5(p-1)]元 ⑤11x+3
18. 解:原式=-9+(-5)=-14
19. 解:原式==
20. 解:原式=
21. 解:
原式====
22. 解:①原式=
②原式=
23. ①解:原式=
当时,上式==
②解:原式==0
当时,上式=0
24. 解:①错误。因为除法不满足结合律。
正确的为:
②错误。一是绝对值为非负数,二是同级运算时应从左往右依次计算。
正确的为:=
25. 解:
答:这批样品平均每听质量比标准每听质量多4克。
26. 解:(1)
(2)当时,
答:当这种蟋蟀每分钟鸣叫56次时,该地当时的气温是34℃。
27. 解:①
②
28. (1)
图形标号
①
②
③
……
⑩
牙签根数
2
7
15
……
155
(2)搭第n个图形需要根牙签
29. 解:
30. 解:
(1)<,<,>,>,>,…
(2)(n≤2);(n≥3)
(3)
【本讲教育信息】
一. 教学内容:
期末复习——有理数、代数式及其运算
二、知识与结构
1. 有理数及其运算
2. 代数式及其运算
三、方法与思考
1. 比较有理数的加法运算律和乘法运算律与小学学过的运算律的异同;
2. 回顾有理数的运算法则,想一想:这与小学学过的运算律有什么不同;
3. 总结有理数运算的基本方法,以及简化运算的技巧,知道哪些数学思想方法?
4. 梳理所学知识,形成一定的体系,并逐步掌握用代数式表达数量关系或变化规律的方法;
5. 理解代数式的含义,能解释一些简单代数式的实际背景或几何意义,体会数学与现实世界的联系;
6. 经历探索事物之间的数量关系,并用字母与代数式表示,建立初步符号感,发展抽象思维.
四、错题回放
1. 代数式书写规范.如a的倍写成a ,应为.
2. 代数式描述语句顺序不理解.如a,b两数的平方和写成,应为.
3. 合并同类项中出错.如,.
4. 去括号中符号出错.如,.
5. 探索规律出错.如由1+3=4=22, 1+3+5=9=32,1+3+5+7=16=42,1+3+5+7+9=25=52,… 猜想1+3+5+7+…+(2n+1)=n2 (n为正整数)21世纪教育网版权所有
【典型例题】
例1. 如图,在数轴上有三个点A、B、C,回答下列问题:
(1)将B点向右移动6个单位,三个点中哪个点所表示的数最小?
(2)将C点向左移动6个单位,三个点中哪个点所表示的数最小?
(3)怎样移动A、B、C中两个点,才能使三个点所表示的数相同?有几种移动方法?
分析:注意移动的方向及相关点所对应的有理数.
解:(1)B点向右移动6个单位就为-1+6=5,所以三个点中A点-2最小;
(2)C点向左移动6个单位就为2-6=-4,所以三个点中C点-4最小;
(3)有三种方法:
①将B点向左移动1个单位;将C点向左移动4个单位;则三个数都为-2
②将A点向右移动1个单位;将C点向左移动3个单位;则三个数都为-1
③将A点向右移动4个单位;将B点向右移动3个单位;则三个数都为2
例2. 有理数a、b、c在数轴上的位置如图所示,其中O是原点,=.
(1)用“<”把a、b、-a、-b连接起来;
(2)b+c的值是多少?
(3)判断a+b与a+c的符号.
分析:比较a、b、-a、-b的大小时,可根据互为相反数的两个数在原点两侧,并且到原点的距离相等这一原理,在数轴上画出表示-a、-b的两点,即可得它们的大小关系.
解:(1)a< b< -b <-a
(2)b+c=0
(3)a+b< 0为“-”; a+c< 0也为“-”
说明:此题也可结合数轴,让问题“具体化”,如取a、b、c的值,算出-a、-b的值,把它们大小比较出来后再“一般化”.21教育网
例3. 计算:
(1);
(2).
分析:(1)对要注意与的区别,许多同学会混淆;
(2)对有理数的混合运算,应先乘方再乘除后加减,如果有括号,还应先进行括号里的运算.第(2)题中每个加数都有,因此可以逆用分配律进行计算.www.21-cn-jy.com
解:(1)原式=
=
=
=
(2)原式=
=
=
例4. 某医院急诊病房收治了一位病人,每隔2时测得该病人的体温如下表(单位:℃)(正常人的体温是37℃)2·1·c·n·j·y
(1)这位病人在这一天8时到18时之间,哪个时刻的体温最高?哪个时刻的体温最低?
(2)该病人这一天的平均体温是多少摄氏度?
(3)以正常体温37℃为原点,用折线图表示该病人体温的变化情况.
时刻
8时
10时
12时
14时
16时
18时
体温
38.5
38.8
39.5
39.6
38
37.5
与正常人的正
常体温的差值
+1.5
+1.8
+2.5
+2.6
+1
+0.5
解:
(1)14时的体温最高;18时的体温最低
(2)[(+1.5)+(+1.8)+(+2.5)+(+2.6)+(+1)+(+0.5)]÷6=1.65
37+1.65=38.65
(3)图略(描点连线)
例5. 3个球队进行单循环比赛(参赛的每个队都与其他队赛一场),总的比赛场数是多少?4个球队呢?写出m个球队进行单循环比赛时总的比赛场数n的公式.【来源:21·世纪·教育·网】
解:3个球队进行单循环比赛要赛3场;
4个球队进行单循环比赛要赛6场;
m个球队进行单循环比赛要赛n=场;
说明:每一个球队都可以有(m-1)场比赛,一共有m个球队,所以有m(m-1)场比赛,但由于是单循环,所以每两个球队只需要赛一场。因此总场数为场。www-2-1-cnjy-com
例6. 先化简,再求值: ,其中.
解:原式=
=
=
当时,上式===
例7. 有若干个数,第1个数记为,第2个数记为,第3个数记为,…,第n个数记为,若,从第2个数起,每一个数都等于“1与它前面的那个数的差的倒数”则① ,= , ;②根据以上结果可知: , .
解:①
=
②根据以上结果可知:3,
说明:由、、、可知,每3个数一个循环,也就是、和3这3个数循环出现。因此我们用1998÷3余0知,应为末尾的3;而1999÷3余1知,则应为第一个数。
【模拟试题】(答题时间:90分钟)
一、选择题:
1. 的相反数是 ( )
A. -2 B. 2 C. D.
2. 如果一个数的平方等于它的倒数,那么这个数一定是 ( )
A. 0 B. 1 C. -1 D. 1或-1
3. 如果两个有理数的和是负数,那么这两个数 ( )
A. 一定都是负数 B. 至少有一个是负数
C. 一定都是非正数 D. 一定是一个正数和一个负数
4. 下列结论中,不正确的是 ( )
A. 1除以非零数的商,叫做这个数的倒数
B. 两个数的积为1,这两个数互为倒数
C. 一个数的倒数一定小于这个数
D. 一个数和它的倒数的商等于这个数的平方
5. 有下列各数,0.01,10,-6.67,,0,-90,-(-3),,,其中属于非负整数的共有 ( )【出处:21教育名师】
A. 1个 B. 2个 C. 3个 D. 4个
6. 下图所示是一个数值转换机,输入x,输出3(x-1),下面给出了四种转换步骤,其中不正确的是 ( )【版权所有:21教育】
A. 先减去1,再乘以3
B. 先乘以3,再减去1
C. 先乘以3,再减去3
D. 先加上-1,再乘以3
7. 下列各组代数式中,不是同类项的是 ( )
A. B. C. D.
8. 如图用火柴棒搭正方形,甲、乙、丙、丁四位同学都用x表示所搭正方形的个数,从而计算火柴棒的根数,他们计算的结果分别是: ( )21教育名师原创作品
甲:4+3(x-1);乙:x+x+(x+1);丙:1+3x;丁:4x-(x-1).
其中计算结果正确的同学有 ( )
A. 1位 B. 2位 C. 3位 D. 4位
二、填空题:
9. 的大小关系: .
10. 绝对值小于4的负整数有 个,正整数有 个,整数有 个.
11. 水池中的水位在某天八个不同时刻测得记录如下(规定上升为正,单位:厘米):
+3,-6,-1,+5,-4,+2,-2,-3,那么这天中水池水位最终的变化情况是 .
12. 数轴上,与表示-2的点的距离为3的数是 .
13. 初一(3)班要添置新桌椅,使每人一套桌椅,其中有x行每行7人,另外还有两行8人,则共需 套桌椅,当x=4时,共需 套桌椅.21*cnjy*com
14. 当m= ,n= 时,和是同类项.
15. 若=7,则= .
16. 已知,,则 , .
17. 列代数式表示
①长方形的周长为20cm,它的宽为xcm,那么它的面积为 ;
②某商品的利润为a元,利润率为10%,此商品进价为 ;
③甲乙两地相距x千米,某人原计划t小时到达,后因故提前1小时到达,则他每小时应比原计划多走 千米;21·cn·jy·com
④托运行李p千克(p为整数)的费用标准:已知托运第1个1千克需付2元,以后每增加1千克(不足1千克按1千克计)需增加费用5角.若某人托运p千克(p>1)的行李,则托运费用为 ;
⑤一个两位数,它的十位数字为x,个位数字比十位数字大3,则这个两位数为
三、计算与化简:
18. ;
19. ;
20. ;
21. .
22. 化简:
① ②
23. 先化简,再求值:
①,其中
②,其中,
四、辨析与思考:
24. ①.
辨析:
②=.
辨析:
五、操作与解释:
25. 某食品厂从生产的食品罐头中,抽出样品20听检查每听的质量,超过和不足标准的部分分别用正、负数表示,记录如下:21cnjy.com
与标准质量的偏差/克
-10
-5
0
+5
+10
+15
听数
1
2
4
7
5
1
问:这批样品平均每听质量比标准每听质量多或少几克?
y(℃)
25
25+2.5
25+5
25+7.5
25+10
…
x(次/分)
20
30
40
50
60
…
26. 生物学家发现,气温y在一定温度内时,某种蟋蟀每分钟鸣叫的次数x与气温y(单位:℃)有一定的关系,下表是通过实验得到的一组数据:21·世纪*教育网
(1)根据表中的数据,写出y与x之间的关系式
(2)当这种蟋蟀每分钟鸣叫56次时,该地当时的气温多少?
27. 小王和小张在玩“24”点游戏,他们互相给对方四张牌,要求对方根据牌上的数字凑成“24”点,他们互给对方的牌上的数字如下:①黑桃1,方块2,红桃2,黑桃3;②方块1,草花3,草花7和红桃12. 请你帮他们凑成“24”点.2-1-c-n-j-y
28. 如图,按一定的规律用牙签搭图形:
(1)按图示的规律填表:
图形标号
①
②
③
……
⑩
牙签根数
……
(2)搭第n个图形需要________________________根牙签.
六、探索与思考:
29. 先观察==1-=
==1-=
再计算的值
30. 你能比较两个数的大小吗?
为了解决这个问题,我们首先把它们抽象成一般形式,即比较的大小(n为自然数),我们从分析特殊向简单的情形入手,令n=1,n=2,n=3,…对其进行分析,从中发现规律,经过归纳,猜想出结论.21*cnjy*com
(1)计算,比较下列各组数中两个数的大小在空格中填“>”、“=”、“<”
, , , , ,…
(2)从上面的结果进行归纳猜想,的大小关系是 .
(3)根据上面的归纳猜想出一般结论,试比较的大小.
【试题答案】
1. D 2. B 3. B 4. C 5. D 6. B 7. C 8. D 【来源:21cnj*y.co*m】
9. > 10. 3;3;7 11. 下降了6个单位 12. -5或1
13. 7x+16;44 14. m=4,n=1 15. 4 16. 4,12
17. ①x(10-x) ②元 ③()千米
④[2+0.5(p-1)]元 ⑤11x+3
18. 解:原式=-9+(-5)=-14
19. 解:原式==
20. 解:原式=
21. 解:
原式====
22. 解:①原式=
②原式=
23. ①解:原式=
当时,上式==
②解:原式==0
当时,上式=0
24. 解:①错误。因为除法不满足结合律。
正确的为:
②错误。一是绝对值为非负数,二是同级运算时应从左往右依次计算。
正确的为:=
25. 解:
答:这批样品平均每听质量比标准每听质量多4克。
26. 解:(1)
(2)当时,
答:当这种蟋蟀每分钟鸣叫56次时,该地当时的气温是34℃。
27. 解:①
②
28. (1)
图形标号
①
②
③
……
⑩
牙签根数
2
7
15
……
155
(2)搭第n个图形需要根牙签
29. 解:
30. 解:
(1)<,<,>,>,>,…
(2)(n≤2);(n≥3)
(3)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
