辽宁省凌海市七年级数学下册课后补习班辅导期中复习及考前模拟讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导期中复习及考前模拟讲学案苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 205.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 07:53:11 | ||
图片预览




文档简介
期中复习及考前模拟
【本讲教育信息】
一. 教学内容:
期中复习及考前模拟
二、知识点
1、“三线八角”
(1)如何由线找角:一看线,二看型。
同位角是“F”型;
内错角是“Z”型;
同旁内角是“U”型。
(2)如何由角找线:组成角的三条线中的公共直线就是截线。
2、平行公理:
如果两条直线都和第三条直线平行,那么这两条直线也平行。
简述:平行于同一条直线的两条直线平行。
补充定理:
如果两条直线都和第三条直线垂直,那么这两条直线也平行。
简述:垂直于同一条直线的两条直线平行。
3、平行线的判定和性质:
判定定理
性质定理
条件
结论
条件
结论
同位角相等
两直线平行
两直线平行
同位角相等
内错角相等
两直线平行
两直线平行
内错角相等
同旁内角互补
两直线平行
两直线平行
同旁内角互补
4、图形平移的性质:
图形经过平移,连接各组对应点所得的线段互相平行(或在同一直线上)并且相等。
5、三角形三边之间的关系:
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边。
若三角形的三边分别为a、b、c,则
6、三角形中的主要线段:三角形的高、角平分线、中线。
[注意]:①三角形的高、角平分线、中线都是线段。
②高、角平分线、中线的应用。
7、三角形的内角和:
三角形的3个内角的和等于180°;
直角三角形的两个锐角互余;
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于与它不相邻的任意一个内角。
8、多边形的内角和:
n边形的内角和等于(n-2)?180°;
任意多边形的外角和等于360°。
9、同底数幂的乘法法则
(m、n是正整数)
10、幂的乘方法则
(m、n是正整数)
11、积的乘方法则
(n是正整数)
12、同底数幂的除法法则
(m、n是正整数,m >n)
13、扩展
(m、n、p是正整数)
14、零指数和负指数法则
(,n是正整数)
15、科学记数法
(1≤a <10,a为整数)
16、单项式乘单项式:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。21教育网
17、单项式乘多项式:
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加。
m(a+b-c)=ma+mb-mc
18、多项式乘多项式:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
(a+b)(c+d)=ac+ad+bc+bd
19、乘法公式:
①完全平方公式:(a+b)2=a2+2ab+b2; (a -b)2=a2-2ab+b2
②平方差公式:(a+b)(a-b)=a2-b2
20、因式分解:
(1)把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
(2)多项式的乘法与多项式因式分解的区别
简单地说:乘法是积化和,因式分解是和化积。
(3)因式分解的方法:
①提公因式法; ②运用公式法。
21、因式分解的应用:
(1)提公因式法:如果多项式的各项含有公因式,那么就可以把这个公因式提出来。把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法。
(2)公因式:多项式ab+ac+ad的各项ab、ac、ad都含有相同的因式a,a称为多项式各项的公因式。21cnjy.com
(3)用提公因式法时的注意点:
①公因式要提尽,考虑的顺序是,先系数,再单独字母,最后多项式。如:
4a2(a-2b)-18ab(a-2b)=2a(a-2b)(2a-9b);
②当多项式的第一项的系数为负数时,把“-”号作为公因式的负号写在括号外,使括号内的第一项的系数为正。如:-2m3+8m2-12m= -2m(m2-4m+6);www-2-1-cnjy-com
③提公因式后,另一个多项式的求法是用原多项式除以公因式。
(4)运用公式法的公式:
①平方差公式:a2-b2=(a+b)(a-b)
②完全平方公式: a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
(5)因式分解的步骤和要求:
把一个多项式分解因式时,应先提公因式,注意公因式要提尽,然后再应用公式,如果是二项式考虑用平方差公式,如果是三项式考虑用完全平方公式,直到把每一个因式都分解到不能再分解为止。
如:-2x5y+4x3y3-2xy5=-2xy(x4-2x2y2+y4)=-2xy(x2-y2) =-2xy(x+y)(x-y)
【典型例题】
例1. ①如图,找出图中所有的同位角 ;
找出图中所有的内错角 ;
找出图中所有的同旁内角 。
②∠BAC和∠ 是 和 被 所截的内错角;
∠BAC和∠ 是 和 被 所截的内错角。
分析:此题在于强化对于“三线八角”的理解,它是平行线应用的基础。
解:①同位角:∠B和∠DCE,∠B和∠ACE
内错角:∠BAC和∠ACD,∠DAC和∠ACB,∠D和∠DCE,∠BAC和∠ACE
同旁内角:∠DAB和∠B,∠DAC和∠ACE,∠D和∠BCD,∠B和∠BCD,∠BAD和∠D,∠B和∠ACB,∠B和∠BAC,∠BAC和∠ACB,∠D和∠DAC,∠D和∠DCA,∠DAC和∠DCA
②∠BAC和∠ACD是AB和CD被AC所截的内错角;
∠BAC和∠ACE是AB和BE被AC所截的内错角。
说明:要想在寻找过程中不遗漏,就要有一定的顺序依次确定三条线。
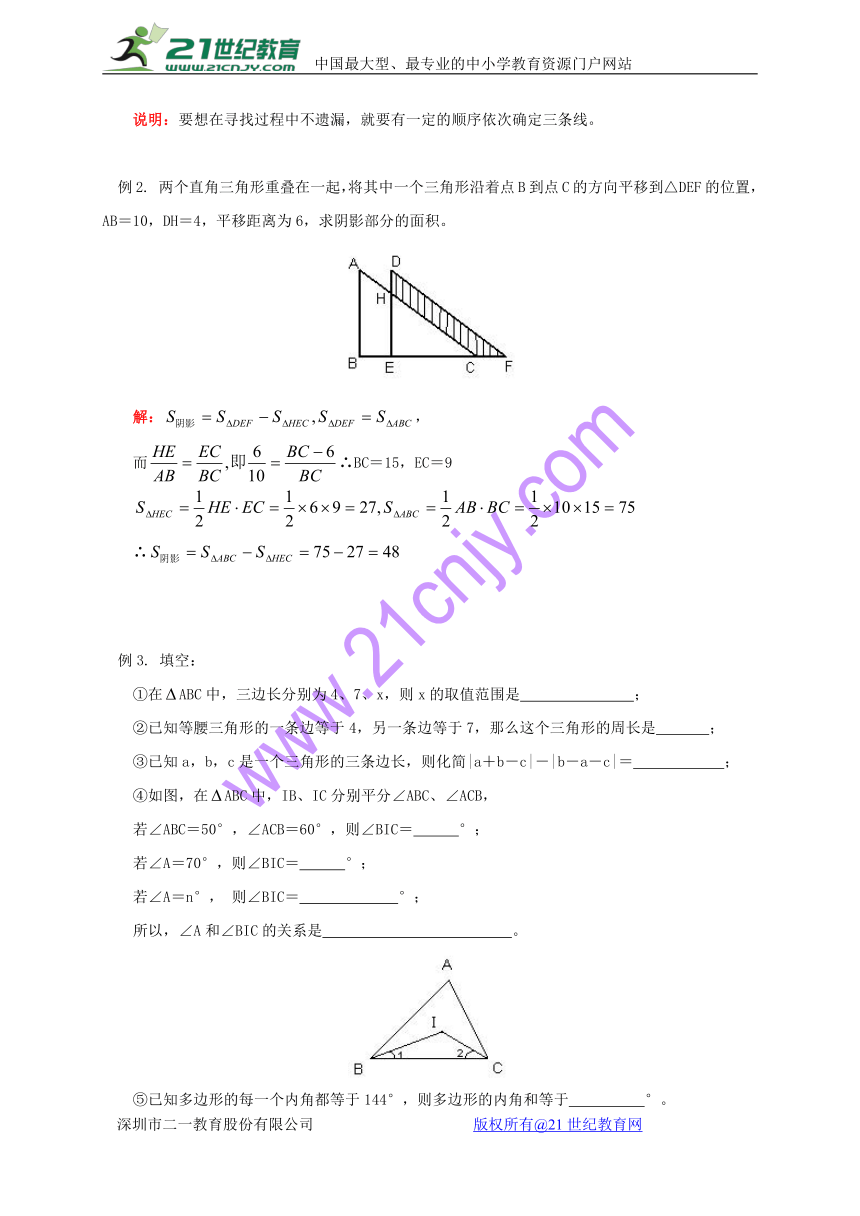
例2. 两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积。
解:,
而∴BC=15,EC=9
∴
例3. 填空:
①在ABC中,三边长分别为4、7、x,则x的取值范围是 ;
②已知等腰三角形的一条边等于4,另一条边等于7,那么这个三角形的周长是 ;
③已知a,b,c是一个三角形的三条边长,则化简|a+b-c|-|b-a-c|= ;
④如图,在ABC中,IB、IC分别平分∠ABC、∠ACB,
若∠ABC=50°,∠ACB=60°,则∠BIC= °;
若∠A=70°,则∠BIC= °;
若∠A=n°, 则∠BIC= °;
所以,∠A和∠BIC的关系是 。
⑤已知多边形的每一个内角都等于144°,则多边形的内角和等于 °。
分析:①三角形两边之和大于第三边,两边之差小于第三边。
②等腰三角形的腰要分类。(但要满足三角形三边的关系)
③由三角形三边的关系知:a+b-c>0,a+c-b>0,则b-a-c<0,根据符号去绝对值。
④角平分线的性质
⑤n边形的内角和等于(n-2)?180°,n边形有n个内角
解:①7-4 ②若等腰三角形的腰为4,则周长=4×2+7=15;若等腰三角形的腰为7则周长=7×2+4=18www.21-cn-jy.com
③|a+b-c|-|b-a-c|= a+b-c+ b-a-c=2b-2c
④若∠ABC=50°,∠ACB=60°,则∠BIC=125°;
若∠A=70°,则∠BIC=125°;
若∠A=n°, 则∠BIC=;
所以,∠A和∠BIC的关系是2∠BIC-∠A =180°。
⑤n?144°=(n-2)?180°,解得:n=10
∴多边形内角和=(n-2)?180°=1440°
例4. 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,
∠DAE=18°,求∠C的度数.
分析:抓住∠DAE这个角的特点,∠DAE=∠DAB-∠BAE
解:∵AD是BC边上的高
∴∠BAD=90°-∠B=90°-42°=48°
又∵∠DAE=∠BAD-∠BAE,
∴∠BAE=∠BAD-∠DAE=48°-18°=30°
而AE是∠BAC的平分线
∴∠BAC=2∠BAE=60°
∴∠C=180°-∠BAC-∠B =180°-60°-42°=78°
例5. 如图,已知在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD
相交于D,试说明∠A=2∠D的理由.
分析:三角形的外角等于不相邻的两个内角和。
解:∵BD平分∠ABC,CD平分∠ACE
∴∠ABO=∠ABC,∠ACD=∠ACE
∵∠A+∠ABO+∠AOB=∠D+∠ACD+∠COD=180°,
而∠AOB=∠COD(对顶角相等)
∴∠A+∠ABO=∠D+∠ACD ,即∠A+∠ABC =∠D+∠ACE
又∵∠ACE=∠A+∠ABC,
∴∠A+∠ABC =∠D+(∠A+∠ABC),即∠A=∠D
∴∠A=2∠D
说明:此题做法不唯一,只要能构造关于∠A、∠D的等式就可得到。
例6. 计算:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)(1-)(1-)(1-)…(1-)(1-)
解:(1)原式==
(2)原式==
(3)原式===
(4)原式===
(5)原式===
(6)原式==
(7)原式===
(8)原式=
(9)原式=
(10)原式=
==…=
(11)原式=(1-)(1+) (1-)(1+) …(1-) (1+)(1-) (1+)
=×××× …××××=×=
例7. 已知am=3, an=2, 求①am+n ②am-n ③a3m ④a2m-3n的值.2·1·c·n·j·y
解:∵am=3, an=2
∴①am+n = am×an=3×2=6 ②am-n= am÷an=3÷2=
③a3m = (am) 3=33=27 ④a2m-3n= (am) 2÷(an) 3=32÷23=【来源:21·世纪·教育·网】
说明:此题在于能很好的区分同底数幂的乘除法与幂的乘方
例8. 求47103的末位数字。
分析:,,,,……
解:47103的末尾数字其实是由个位7的乘积得到的,而我们看7的乘方的个位数字的变化是有规律的:每四个一个循环——7、9、3、1,所以计算103÷4=25…3。21·世纪*教育网
∴47103的末位数字为3。
例9. 填空
(1)若,则= ;
(2)若m2+n2-6n+4m+13=0,则m2-n2 =_________;
(3)若,则 , ;
(4)若,则 ;
(5)若那么= ;
(6)已知2m=x,43m=y,用含有字母x 的代数式表示y,则y=_____________。
分析:(1)待定系数法
(2)把m2+n2-6n+4m+13配成完全平方,它们是非负数
(3)完全平方式的活用。
(4)(5)整体思想
解:(1)∵
∴
∴ 解得∴
(2)m2+n2-6n+4m+13=(m+2)2 +(n-3)2=0
∴m=-2,n=3 ∴m2-n2=4-9=-5
(3)∵,
∴,
(4)∵,
∴,
∴
(5)
∴∴=6
(6)y=43m=26m=(2m)6=x6
例10. 分解因式:
(1)a(x-y)+b(y-x)+c(x-y) (2)4(a+b)2-9(a-b)2
(3)(x2-2xy)2+2y2(x2-2xy)+y4 (4)x4-81 21世纪教育网版权所有
(5) (x+y)2-4(x2-y2)+4(x-y)2 (6)16a4-8a2+1 2-1-c-n-j-y
(7)(x2+4)2-16x2 *(8)
解:(1)原式= a(x-y) -b(x-y)+c(x-y)= (a-b +c) (x-y)
(2)原式=[2(a+b)]2-[3(a-b)]2=[2(a+b)+3(a-b)] [2(a+b)]-[3(a-b)] =-(5a-b)(a-5b)【出处:21教育名师】
(3)原式=(x2-2xy+y2)2= (x-y)4
(4)原式=(x2-9)(x2+9)= (x-3)(x+3)(x2+9)
(5)原式=(x+y)2-4(x+y) (x-y)+4(x-y)2 =[(x+y) -2(x-y) ] 2 = (x-3y)2
(6)原式=
(7)原式=(x2+4+4x)(x2+4-4x)=(x+2)(x-2)
(8) 原式=
例11. 已知m、n为自然数,且m(m-n)-n (n-m)=7,求m、n的值。
分析:解题的关键在于条件:m、n为自然数。
解:m(m-n)-n (n-m)= (m+n) (m-n)=7
∵m、n为自然数,
∴m+n和m-n也为自然数,
∴m+n=7,m-n=1,
∴m=4,n=3
说明:7为质数,则其因数只有1与其本身。
【模拟试题】(答题时间:90分钟)
一. 选择题 (2分×10=20分)
1. 下列运算正确的是( )
A. (2a-3b)2=4a2 –9b2 B. (a+b)2=a2+b2
C. (a+b)2=a2+ab+b2 D. (0.3a-0.2b)2=a2+ab+b2
2. 下列多项式的乘法中,可以用平方差公式计算的是( )
A. (x+1)(1+x) B. (a+b)(b-a)
C. (-a+b)(a-b) D. (x2-y)(x+y2)
3. 已知(a+b)2=11,(a-b)2=7,则2ab为( )
A. 2 B. –1 C. 1 D. –221教育名师原创作品
4. 方程x+y=4有几个正整数解( )
A. 1个 B. 2个 C. 3个 D. 4个21*cnjy*com
5. 在y=kx+b中,当x=2时,y=8,当x=-1时,y=-7,则k , b的值是( )
A. k=5 , b=-2 B. k=5 , b=2
C. k=-5 , b=-2 D. k=–5 , b=2
6. 若两平行直线EF,MN与相交直线AB,CD相交成如图所示的图形,则图中共有同旁内角的对数是( )
A. 4 B. 8 C. 12 D. 16
7. 如图所示AB∥CD,EF⊥CD,FG平分∠EFC,则( )
A. ∠1>∠2 B. ∠1<∠2
C. ∠1=∠2 D. 不能确定
8. 如图,DE∥AB,∠CAE=∠CAB,∠CDE=75o, ∠B=65o,则∠AEB是( )
A. 70o B. 65o
C. 60o D. 55o
9. △ABC中,如果∠A-∠B=90o,那么△ABC是( )
A. 钝角三角形 B. 锐角三角形
C. 直角三角形 D. 锐角或钝角三角形
10. 一辆汽车在笔直的公路上行驶,两次转弯后,仍在原来的方向上平行前进,那么这两次转弯的角度应是( )21·cn·jy·com
A. 第一次向右转40o,第二次向左转140o
B. 第一次向左转40o,第二次向右转40o
C. 第一次向左转40o,第二次向右转140o
D. 第一次向右转40o,第二次向右转40o
二. 填空题 (2分×14=28分)
11. 单项式-4ab,3ab,-b2的积是________
12. 化简3xy-3(4yx-2x)+(2xy-2y)=_______
13. 若3a3bn-5amb4所得的差是单项式,则这个单项式是________
14. 如图,我国国旗上的五角星的每一个顶角都相等,其度数是________
15. 空气的体积质量是1.239×10-3g/cm3 ,用小数把它表示出来为________g/cm3
16. 若长方形的宽是a×103cm,长是宽的2倍,则长方形的面积为_______cm2
17. 已知a2-Nab+64b2是一个完全平方式,则N等于_______
18. 若│2x-y-3│与(x+2y+1)2互为相反数,则x=______y=______
19. 某哨卡运回一箱苹果,若每个战士分6个,则少6个,若每个战士分5个则多5个,那么这个哨卡共有_______名战士,箱中共有________个苹果。21*cnjy*com
20. 如图∠1=∠2,∠BAD=60o,则∠B=_______
21. 如图,把一张长方形的纸片ABCD折叠,使点C与点A重合,折痕为EF,如果∠DEF=123o,那么∠BAF=_________。【版权所有:21教育】
22. 如图AOB是一钢架,且∠AOB=10o,为了使钢架更加坚固,需要在其内部添加一些钢管EF,FG,GH,……添加的钢管长度都与OE相等,则最多能添加这样的钢管_______根。
三. 解答题。(23,24,25题每题6分,26,27题每题8分,28,29题,每题9分)
23. 计算式()2·(-)-2-(1.75-)0+2-1。
24. 已知a(a-1)-(a2-b)=5,求-ab的值。
25. 若方程组的解相同,求a+b的值。
26. 如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为x的小正方形,按折痕做一个有底无盖的长方形盒子,试求盒子的体积。【来源:21cnj*y.co*m】
27. 已知如图△ABC中,AD⊥BC于D,DE∥AB交AC于E,那么∠BAD与∠EDC有何关系?为什么?
28. 某旅游团一行50人到某旅社住宿,该旅社有三人间,双人间和单人间三种客房,其中三人间每人每晚20元,双人间每人每晚30元,单人间每晚50元,已知该旅游团住满了20间客房,且使总的住宿费用最省,那么这笔费用共多少钱?所住的三人间,双人间,单人间各多少间?
29. 对于有理数x,y定义一种运算“△”:x△y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法和乘法运算.已知3△5=15,4△7=28,求(1△1)的值.
【试题答案】
一. 选择题:
1. C 2. B 3. C 4. C 5. A
6. D 7. C 8. B 9. A 10. B
二. 填空题:
11. 12a2b4 12. -7xy+6x-2y
13. -2a3b4 14.36 o 15. 0.001239
16. ×106 17.
18. x=1,y=-1 19. 11,60
20. 120o 21. 24o 22. 8
三. 解答题:
23. 24.
25.
26.
27. 互余关系
∵AB∥DE,∴∠B=∠EDC
∵AD⊥BC ∴∠ADB=90° ∠BAD与∠B互余
∴∠BAD与∠EDC 互余
28. 住宿费用1150元。 三人间、双人间、单人间依次为15,0,5
29.
解得
故△=a+b+c=(-35-2c)+(24+c)+c=-11
【本讲教育信息】
一. 教学内容:
期中复习及考前模拟
二、知识点
1、“三线八角”
(1)如何由线找角:一看线,二看型。
同位角是“F”型;
内错角是“Z”型;
同旁内角是“U”型。
(2)如何由角找线:组成角的三条线中的公共直线就是截线。
2、平行公理:
如果两条直线都和第三条直线平行,那么这两条直线也平行。
简述:平行于同一条直线的两条直线平行。
补充定理:
如果两条直线都和第三条直线垂直,那么这两条直线也平行。
简述:垂直于同一条直线的两条直线平行。
3、平行线的判定和性质:
判定定理
性质定理
条件
结论
条件
结论
同位角相等
两直线平行
两直线平行
同位角相等
内错角相等
两直线平行
两直线平行
内错角相等
同旁内角互补
两直线平行
两直线平行
同旁内角互补
4、图形平移的性质:
图形经过平移,连接各组对应点所得的线段互相平行(或在同一直线上)并且相等。
5、三角形三边之间的关系:
三角形的任意两边之和大于第三边;
三角形的任意两边之差小于第三边。
若三角形的三边分别为a、b、c,则
6、三角形中的主要线段:三角形的高、角平分线、中线。
[注意]:①三角形的高、角平分线、中线都是线段。
②高、角平分线、中线的应用。
7、三角形的内角和:
三角形的3个内角的和等于180°;
直角三角形的两个锐角互余;
三角形的一个外角等于与它不相邻的两个内角的和;
三角形的一个外角大于与它不相邻的任意一个内角。
8、多边形的内角和:
n边形的内角和等于(n-2)?180°;
任意多边形的外角和等于360°。
9、同底数幂的乘法法则
(m、n是正整数)
10、幂的乘方法则
(m、n是正整数)
11、积的乘方法则
(n是正整数)
12、同底数幂的除法法则
(m、n是正整数,m >n)
13、扩展
(m、n、p是正整数)
14、零指数和负指数法则
(,n是正整数)
15、科学记数法
(1≤a <10,a为整数)
16、单项式乘单项式:
单项式与单项式相乘,把它们的系数、相同字母的幂分别相乘,对于只在一个单项式里含有的字母,则连同它的指数作为积的一个因式。21教育网
17、单项式乘多项式:
单项式与多项式相乘,用单项式乘多项式的每一项,再把所得的积相加。
m(a+b-c)=ma+mb-mc
18、多项式乘多项式:
多项式与多项式相乘,先用一个多项式的每一项乘另一个多项式的每一项,再把所得的积相加。
(a+b)(c+d)=ac+ad+bc+bd
19、乘法公式:
①完全平方公式:(a+b)2=a2+2ab+b2; (a -b)2=a2-2ab+b2
②平方差公式:(a+b)(a-b)=a2-b2
20、因式分解:
(1)把一个多项式写成几个整式的积的形式叫做多项式的因式分解。
(2)多项式的乘法与多项式因式分解的区别
简单地说:乘法是积化和,因式分解是和化积。
(3)因式分解的方法:
①提公因式法; ②运用公式法。
21、因式分解的应用:
(1)提公因式法:如果多项式的各项含有公因式,那么就可以把这个公因式提出来。把多项式化成公因式与另一个多项式的积的形式,这种分解因式的方法叫做提公因式法。
(2)公因式:多项式ab+ac+ad的各项ab、ac、ad都含有相同的因式a,a称为多项式各项的公因式。21cnjy.com
(3)用提公因式法时的注意点:
①公因式要提尽,考虑的顺序是,先系数,再单独字母,最后多项式。如:
4a2(a-2b)-18ab(a-2b)=2a(a-2b)(2a-9b);
②当多项式的第一项的系数为负数时,把“-”号作为公因式的负号写在括号外,使括号内的第一项的系数为正。如:-2m3+8m2-12m= -2m(m2-4m+6);www-2-1-cnjy-com
③提公因式后,另一个多项式的求法是用原多项式除以公因式。
(4)运用公式法的公式:
①平方差公式:a2-b2=(a+b)(a-b)
②完全平方公式: a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
(5)因式分解的步骤和要求:
把一个多项式分解因式时,应先提公因式,注意公因式要提尽,然后再应用公式,如果是二项式考虑用平方差公式,如果是三项式考虑用完全平方公式,直到把每一个因式都分解到不能再分解为止。
如:-2x5y+4x3y3-2xy5=-2xy(x4-2x2y2+y4)=-2xy(x2-y2) =-2xy(x+y)(x-y)
【典型例题】
例1. ①如图,找出图中所有的同位角 ;
找出图中所有的内错角 ;
找出图中所有的同旁内角 。
②∠BAC和∠ 是 和 被 所截的内错角;
∠BAC和∠ 是 和 被 所截的内错角。
分析:此题在于强化对于“三线八角”的理解,它是平行线应用的基础。
解:①同位角:∠B和∠DCE,∠B和∠ACE
内错角:∠BAC和∠ACD,∠DAC和∠ACB,∠D和∠DCE,∠BAC和∠ACE
同旁内角:∠DAB和∠B,∠DAC和∠ACE,∠D和∠BCD,∠B和∠BCD,∠BAD和∠D,∠B和∠ACB,∠B和∠BAC,∠BAC和∠ACB,∠D和∠DAC,∠D和∠DCA,∠DAC和∠DCA
②∠BAC和∠ACD是AB和CD被AC所截的内错角;
∠BAC和∠ACE是AB和BE被AC所截的内错角。
说明:要想在寻找过程中不遗漏,就要有一定的顺序依次确定三条线。
例2. 两个直角三角形重叠在一起,将其中一个三角形沿着点B到点C的方向平移到△DEF的位置,AB=10,DH=4,平移距离为6,求阴影部分的面积。
解:,
而∴BC=15,EC=9
∴
例3. 填空:
①在ABC中,三边长分别为4、7、x,则x的取值范围是 ;
②已知等腰三角形的一条边等于4,另一条边等于7,那么这个三角形的周长是 ;
③已知a,b,c是一个三角形的三条边长,则化简|a+b-c|-|b-a-c|= ;
④如图,在ABC中,IB、IC分别平分∠ABC、∠ACB,
若∠ABC=50°,∠ACB=60°,则∠BIC= °;
若∠A=70°,则∠BIC= °;
若∠A=n°, 则∠BIC= °;
所以,∠A和∠BIC的关系是 。
⑤已知多边形的每一个内角都等于144°,则多边形的内角和等于 °。
分析:①三角形两边之和大于第三边,两边之差小于第三边。
②等腰三角形的腰要分类。(但要满足三角形三边的关系)
③由三角形三边的关系知:a+b-c>0,a+c-b>0,则b-a-c<0,根据符号去绝对值。
④角平分线的性质
⑤n边形的内角和等于(n-2)?180°,n边形有n个内角
解:①7-4
③|a+b-c|-|b-a-c|= a+b-c+ b-a-c=2b-2c
④若∠ABC=50°,∠ACB=60°,则∠BIC=125°;
若∠A=70°,则∠BIC=125°;
若∠A=n°, 则∠BIC=;
所以,∠A和∠BIC的关系是2∠BIC-∠A =180°。
⑤n?144°=(n-2)?180°,解得:n=10
∴多边形内角和=(n-2)?180°=1440°
例4. 如图,△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,
∠DAE=18°,求∠C的度数.
分析:抓住∠DAE这个角的特点,∠DAE=∠DAB-∠BAE
解:∵AD是BC边上的高
∴∠BAD=90°-∠B=90°-42°=48°
又∵∠DAE=∠BAD-∠BAE,
∴∠BAE=∠BAD-∠DAE=48°-18°=30°
而AE是∠BAC的平分线
∴∠BAC=2∠BAE=60°
∴∠C=180°-∠BAC-∠B =180°-60°-42°=78°
例5. 如图,已知在△ABC中,BD平分∠ABC,CD平分△ABC的外角∠ACE,BD、CD
相交于D,试说明∠A=2∠D的理由.
分析:三角形的外角等于不相邻的两个内角和。
解:∵BD平分∠ABC,CD平分∠ACE
∴∠ABO=∠ABC,∠ACD=∠ACE
∵∠A+∠ABO+∠AOB=∠D+∠ACD+∠COD=180°,
而∠AOB=∠COD(对顶角相等)
∴∠A+∠ABO=∠D+∠ACD ,即∠A+∠ABC =∠D+∠ACE
又∵∠ACE=∠A+∠ABC,
∴∠A+∠ABC =∠D+(∠A+∠ABC),即∠A=∠D
∴∠A=2∠D
说明:此题做法不唯一,只要能构造关于∠A、∠D的等式就可得到。
例6. 计算:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)(1-)(1-)(1-)…(1-)(1-)
解:(1)原式==
(2)原式==
(3)原式===
(4)原式===
(5)原式===
(6)原式==
(7)原式===
(8)原式=
(9)原式=
(10)原式=
==…=
(11)原式=(1-)(1+) (1-)(1+) …(1-) (1+)(1-) (1+)
=×××× …××××=×=
例7. 已知am=3, an=2, 求①am+n ②am-n ③a3m ④a2m-3n的值.2·1·c·n·j·y
解:∵am=3, an=2
∴①am+n = am×an=3×2=6 ②am-n= am÷an=3÷2=
③a3m = (am) 3=33=27 ④a2m-3n= (am) 2÷(an) 3=32÷23=【来源:21·世纪·教育·网】
说明:此题在于能很好的区分同底数幂的乘除法与幂的乘方
例8. 求47103的末位数字。
分析:,,,,……
解:47103的末尾数字其实是由个位7的乘积得到的,而我们看7的乘方的个位数字的变化是有规律的:每四个一个循环——7、9、3、1,所以计算103÷4=25…3。21·世纪*教育网
∴47103的末位数字为3。
例9. 填空
(1)若,则= ;
(2)若m2+n2-6n+4m+13=0,则m2-n2 =_________;
(3)若,则 , ;
(4)若,则 ;
(5)若那么= ;
(6)已知2m=x,43m=y,用含有字母x 的代数式表示y,则y=_____________。
分析:(1)待定系数法
(2)把m2+n2-6n+4m+13配成完全平方,它们是非负数
(3)完全平方式的活用。
(4)(5)整体思想
解:(1)∵
∴
∴ 解得∴
(2)m2+n2-6n+4m+13=(m+2)2 +(n-3)2=0
∴m=-2,n=3 ∴m2-n2=4-9=-5
(3)∵,
∴,
(4)∵,
∴,
∴
(5)
∴∴=6
(6)y=43m=26m=(2m)6=x6
例10. 分解因式:
(1)a(x-y)+b(y-x)+c(x-y) (2)4(a+b)2-9(a-b)2
(3)(x2-2xy)2+2y2(x2-2xy)+y4 (4)x4-81 21世纪教育网版权所有
(5) (x+y)2-4(x2-y2)+4(x-y)2 (6)16a4-8a2+1 2-1-c-n-j-y
(7)(x2+4)2-16x2 *(8)
解:(1)原式= a(x-y) -b(x-y)+c(x-y)= (a-b +c) (x-y)
(2)原式=[2(a+b)]2-[3(a-b)]2=[2(a+b)+3(a-b)] [2(a+b)]-[3(a-b)] =-(5a-b)(a-5b)【出处:21教育名师】
(3)原式=(x2-2xy+y2)2= (x-y)4
(4)原式=(x2-9)(x2+9)= (x-3)(x+3)(x2+9)
(5)原式=(x+y)2-4(x+y) (x-y)+4(x-y)2 =[(x+y) -2(x-y) ] 2 = (x-3y)2
(6)原式=
(7)原式=(x2+4+4x)(x2+4-4x)=(x+2)(x-2)
(8) 原式=
例11. 已知m、n为自然数,且m(m-n)-n (n-m)=7,求m、n的值。
分析:解题的关键在于条件:m、n为自然数。
解:m(m-n)-n (n-m)= (m+n) (m-n)=7
∵m、n为自然数,
∴m+n和m-n也为自然数,
∴m+n=7,m-n=1,
∴m=4,n=3
说明:7为质数,则其因数只有1与其本身。
【模拟试题】(答题时间:90分钟)
一. 选择题 (2分×10=20分)
1. 下列运算正确的是( )
A. (2a-3b)2=4a2 –9b2 B. (a+b)2=a2+b2
C. (a+b)2=a2+ab+b2 D. (0.3a-0.2b)2=a2+ab+b2
2. 下列多项式的乘法中,可以用平方差公式计算的是( )
A. (x+1)(1+x) B. (a+b)(b-a)
C. (-a+b)(a-b) D. (x2-y)(x+y2)
3. 已知(a+b)2=11,(a-b)2=7,则2ab为( )
A. 2 B. –1 C. 1 D. –221教育名师原创作品
4. 方程x+y=4有几个正整数解( )
A. 1个 B. 2个 C. 3个 D. 4个21*cnjy*com
5. 在y=kx+b中,当x=2时,y=8,当x=-1时,y=-7,则k , b的值是( )
A. k=5 , b=-2 B. k=5 , b=2
C. k=-5 , b=-2 D. k=–5 , b=2
6. 若两平行直线EF,MN与相交直线AB,CD相交成如图所示的图形,则图中共有同旁内角的对数是( )
A. 4 B. 8 C. 12 D. 16
7. 如图所示AB∥CD,EF⊥CD,FG平分∠EFC,则( )
A. ∠1>∠2 B. ∠1<∠2
C. ∠1=∠2 D. 不能确定
8. 如图,DE∥AB,∠CAE=∠CAB,∠CDE=75o, ∠B=65o,则∠AEB是( )
A. 70o B. 65o
C. 60o D. 55o
9. △ABC中,如果∠A-∠B=90o,那么△ABC是( )
A. 钝角三角形 B. 锐角三角形
C. 直角三角形 D. 锐角或钝角三角形
10. 一辆汽车在笔直的公路上行驶,两次转弯后,仍在原来的方向上平行前进,那么这两次转弯的角度应是( )21·cn·jy·com
A. 第一次向右转40o,第二次向左转140o
B. 第一次向左转40o,第二次向右转40o
C. 第一次向左转40o,第二次向右转140o
D. 第一次向右转40o,第二次向右转40o
二. 填空题 (2分×14=28分)
11. 单项式-4ab,3ab,-b2的积是________
12. 化简3xy-3(4yx-2x)+(2xy-2y)=_______
13. 若3a3bn-5amb4所得的差是单项式,则这个单项式是________
14. 如图,我国国旗上的五角星的每一个顶角都相等,其度数是________
15. 空气的体积质量是1.239×10-3g/cm3 ,用小数把它表示出来为________g/cm3
16. 若长方形的宽是a×103cm,长是宽的2倍,则长方形的面积为_______cm2
17. 已知a2-Nab+64b2是一个完全平方式,则N等于_______
18. 若│2x-y-3│与(x+2y+1)2互为相反数,则x=______y=______
19. 某哨卡运回一箱苹果,若每个战士分6个,则少6个,若每个战士分5个则多5个,那么这个哨卡共有_______名战士,箱中共有________个苹果。21*cnjy*com
20. 如图∠1=∠2,∠BAD=60o,则∠B=_______
21. 如图,把一张长方形的纸片ABCD折叠,使点C与点A重合,折痕为EF,如果∠DEF=123o,那么∠BAF=_________。【版权所有:21教育】
22. 如图AOB是一钢架,且∠AOB=10o,为了使钢架更加坚固,需要在其内部添加一些钢管EF,FG,GH,……添加的钢管长度都与OE相等,则最多能添加这样的钢管_______根。
三. 解答题。(23,24,25题每题6分,26,27题每题8分,28,29题,每题9分)
23. 计算式()2·(-)-2-(1.75-)0+2-1。
24. 已知a(a-1)-(a2-b)=5,求-ab的值。
25. 若方程组的解相同,求a+b的值。
26. 如图,长为10cm,宽为6cm的长方形,在4个角剪去4个边长为x的小正方形,按折痕做一个有底无盖的长方形盒子,试求盒子的体积。【来源:21cnj*y.co*m】
27. 已知如图△ABC中,AD⊥BC于D,DE∥AB交AC于E,那么∠BAD与∠EDC有何关系?为什么?
28. 某旅游团一行50人到某旅社住宿,该旅社有三人间,双人间和单人间三种客房,其中三人间每人每晚20元,双人间每人每晚30元,单人间每晚50元,已知该旅游团住满了20间客房,且使总的住宿费用最省,那么这笔费用共多少钱?所住的三人间,双人间,单人间各多少间?
29. 对于有理数x,y定义一种运算“△”:x△y=ax+by+c,其中a,b,c为常数,等式右边是通常的加法和乘法运算.已知3△5=15,4△7=28,求(1△1)的值.
【试题答案】
一. 选择题:
1. C 2. B 3. C 4. C 5. A
6. D 7. C 8. B 9. A 10. B
二. 填空题:
11. 12a2b4 12. -7xy+6x-2y
13. -2a3b4 14.36 o 15. 0.001239
16. ×106 17.
18. x=1,y=-1 19. 11,60
20. 120o 21. 24o 22. 8
三. 解答题:
23. 24.
25.
26.
27. 互余关系
∵AB∥DE,∴∠B=∠EDC
∵AD⊥BC ∴∠ADB=90° ∠BAD与∠B互余
∴∠BAD与∠EDC 互余
28. 住宿费用1150元。 三人间、双人间、单人间依次为15,0,5
29.
解得
故△=a+b+c=(-35-2c)+(24+c)+c=-11
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
