辽宁省凌海市七年级数学下册课后补习班辅导三视图讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导三视图讲学案苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 328.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 07:59:35 | ||
图片预览

文档简介
三视图
【本讲教育信息】
一.
教学内容:
三视图
二.
教学目标:
1.
初步体会从不同方向观察同一物体可能看到不同的结果
2.
能识别简单物体的三视图,会画简单立方体及其简单组合的三视图
三.
重点、难点:
1.
体会从不同方向观察同一物体可能看到不同的结果
2.
能画简单立方体及其简单组合的三视图
四.
知识要点
1.
我们从不同的方向观察同一个事物,可能会看到不同的结果,其中我们重点研究以下三个方向看到的图,即:
主视图:从正面看到的图形
左视图:从左面看到的图形
俯视图:从上面看到的图形
统称为“三视图”
【典型例题】
例1.
桌面上放两件物体,它们的三视图如下图示,则这两个物体分别是________,它们的位置是______
。
解:主视图、俯视图、左视图分别为长方形、圆、长方体的物体为圆柱;主视图、俯视图、左视图分别都为长方形的物体为长方体。
由第一、二幅图知:这两个物体分别是圆柱,它们的位置是在长方体前面。
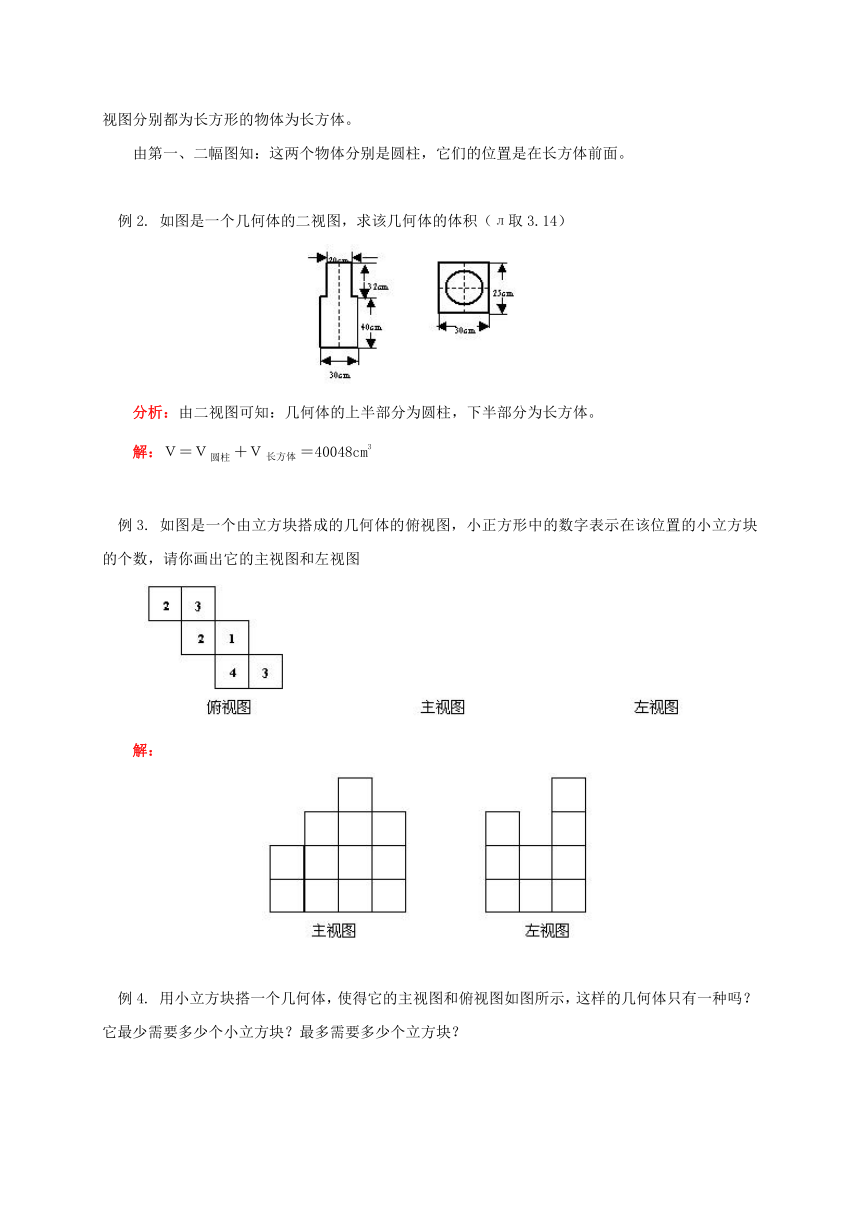
例2.
如图是一个几何体的二视图,求该几何体的体积(л取3.14)
分析:由二视图可知:几何体的上半部分为圆柱,下半部分为长方体。
解:V=V+V=40048cm3
例3.
如图是一个由立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请你画出它的主视图和左视图
解:
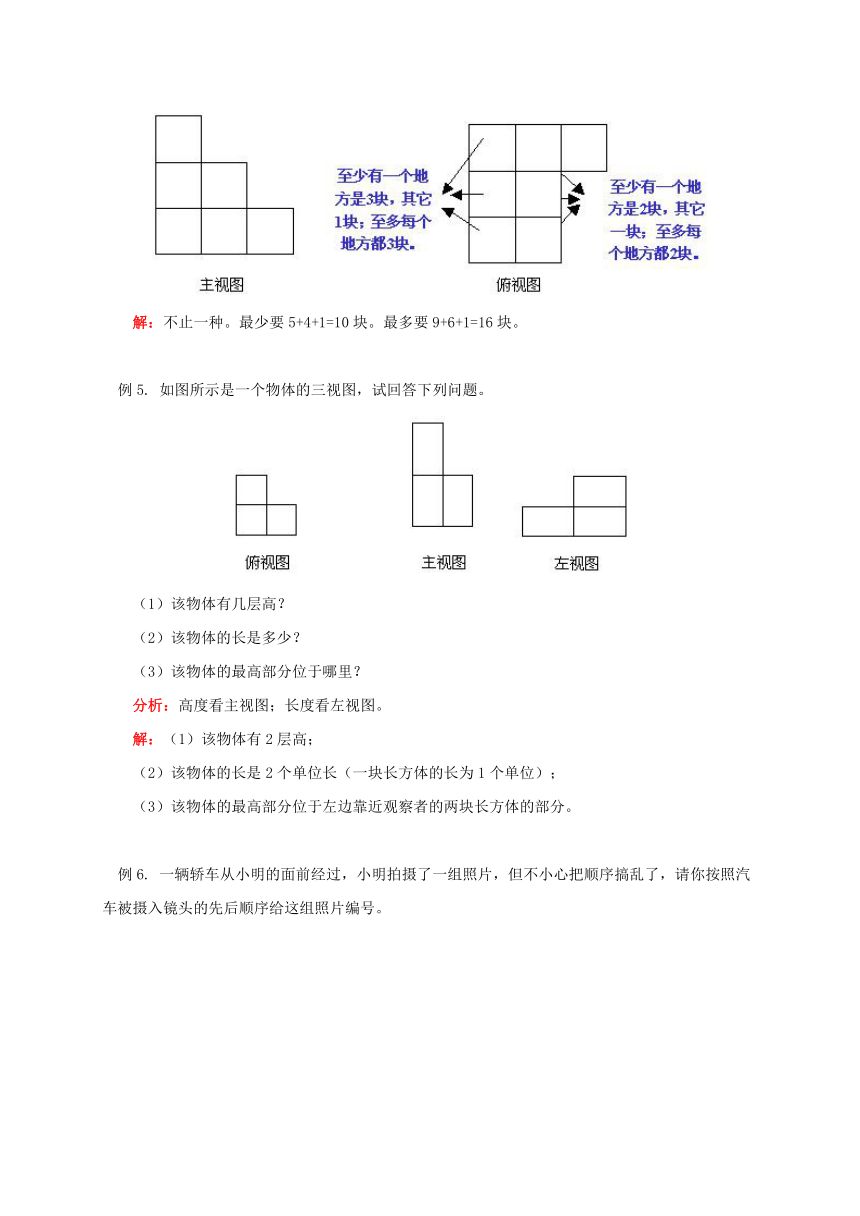
例4.
用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个立方块?
解:不止一种。最少要5+4+1=10块。最多要9+6+1=16块。
例5.
如图所示是一个物体的三视图,试回答下列问题。
(1)该物体有几层高?
(2)该物体的长是多少?
(3)该物体的最高部分位于哪里?
分析:高度看主视图;长度看左视图。
解:(1)该物体有2层高;
(2)该物体的长是2个单位长(一块长方体的长为1个单位);
(3)该物体的最高部分位于左边靠近观察者的两块长方体的部分。
例6.
一辆轿车从小明的面前经过,小明拍摄了一组照片,但不小心把顺序搞乱了,请你按照汽车被摄入镜头的先后顺序给这组照片编号。
分析:车子从远及近,所以先看到正面,再看到侧面,最后看到背面。
解:1-3-2-4
说明:若是倒车则顺序反过来。
【模拟试题】(答题时间:30分钟)
1.
长方体的三视图是(
)
A.
三个正方形
B.
三个一样大的长方形
C.
三个大小不一样的长方形,或其中可能有两个大小一样
D.
三个大小都不同的长方形
2.
一个物体的三视图是下面三个图形,则该物体形状的名称为(
)
A.
圆柱
B.
棱柱
C.
圆锥
D.
球
3.
如图是由一些相同的小正方体构成的立体图形的三种视图.
那么构成这个立体图形的小正方体有(
)
A.
4个
B.
5个
C.
6个
D.
7个
4.
甲、乙、丙、丁四人分别面对面从在一个四边形桌子旁边,桌上一张纸写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是(
)
A.
甲在丁的对面,乙在甲的左边,丙在丁的右边
B.
丙在乙的对面,丙的左边是甲,右边是乙
C.
甲在乙的对面,甲的右边是丙,左边是丁
D.
甲在丁的对面,乙在甲的右边,丙在丁的右边
5.
如图甲是从(
)面看到的图乙的图形。
6.
一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体在课桌上摆成如图形式,然后把露出的表面上不同颜色,则被涂上颜色部分的面积为
。
7.
下面图形是由小正方体木块搭成的几何体的三视图示意图,则该几何体的实物图形是什么模样的 它由多少个小正方体木块搭成。请用小木块实地操作一下吧!
8.
画出下面几何体的主视图、左视图与俯视图。
9.
如图是由几个小正方体块所搭几何体的俯视图,小正方体中的数字表示在该位置小立方块的个数。请画出这个几何体的主视图和左视图。
10.
画出下列几何体的三种视图
【试题答案】
1.
C
2.
C
3.
B
4.
D
5.
上
6.
S=33分米2
7.
图略。共7块。
8.
这个几何体的主视图、左视图与俯视图分别是:
9.
10.
(1)
【本讲教育信息】
一.
教学内容:
三视图
二.
教学目标:
1.
初步体会从不同方向观察同一物体可能看到不同的结果
2.
能识别简单物体的三视图,会画简单立方体及其简单组合的三视图
三.
重点、难点:
1.
体会从不同方向观察同一物体可能看到不同的结果
2.
能画简单立方体及其简单组合的三视图
四.
知识要点
1.
我们从不同的方向观察同一个事物,可能会看到不同的结果,其中我们重点研究以下三个方向看到的图,即:
主视图:从正面看到的图形
左视图:从左面看到的图形
俯视图:从上面看到的图形
统称为“三视图”
【典型例题】
例1.
桌面上放两件物体,它们的三视图如下图示,则这两个物体分别是________,它们的位置是______
。
解:主视图、俯视图、左视图分别为长方形、圆、长方体的物体为圆柱;主视图、俯视图、左视图分别都为长方形的物体为长方体。
由第一、二幅图知:这两个物体分别是圆柱,它们的位置是在长方体前面。
例2.
如图是一个几何体的二视图,求该几何体的体积(л取3.14)
分析:由二视图可知:几何体的上半部分为圆柱,下半部分为长方体。
解:V=V+V=40048cm3
例3.
如图是一个由立方块搭成的几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,请你画出它的主视图和左视图
解:
例4.
用小立方块搭一个几何体,使得它的主视图和俯视图如图所示,这样的几何体只有一种吗?它最少需要多少个小立方块?最多需要多少个立方块?
解:不止一种。最少要5+4+1=10块。最多要9+6+1=16块。
例5.
如图所示是一个物体的三视图,试回答下列问题。
(1)该物体有几层高?
(2)该物体的长是多少?
(3)该物体的最高部分位于哪里?
分析:高度看主视图;长度看左视图。
解:(1)该物体有2层高;
(2)该物体的长是2个单位长(一块长方体的长为1个单位);
(3)该物体的最高部分位于左边靠近观察者的两块长方体的部分。
例6.
一辆轿车从小明的面前经过,小明拍摄了一组照片,但不小心把顺序搞乱了,请你按照汽车被摄入镜头的先后顺序给这组照片编号。
分析:车子从远及近,所以先看到正面,再看到侧面,最后看到背面。
解:1-3-2-4
说明:若是倒车则顺序反过来。
【模拟试题】(答题时间:30分钟)
1.
长方体的三视图是(
)
A.
三个正方形
B.
三个一样大的长方形
C.
三个大小不一样的长方形,或其中可能有两个大小一样
D.
三个大小都不同的长方形
2.
一个物体的三视图是下面三个图形,则该物体形状的名称为(
)
A.
圆柱
B.
棱柱
C.
圆锥
D.
球
3.
如图是由一些相同的小正方体构成的立体图形的三种视图.
那么构成这个立体图形的小正方体有(
)
A.
4个
B.
5个
C.
6个
D.
7个
4.
甲、乙、丙、丁四人分别面对面从在一个四边形桌子旁边,桌上一张纸写着数字“9”,甲说他看到的是“6”,乙说他看到的是“”,丙说他看到的是“”,丁说他看到的是“9”,则下列说法正确的是(
)
A.
甲在丁的对面,乙在甲的左边,丙在丁的右边
B.
丙在乙的对面,丙的左边是甲,右边是乙
C.
甲在乙的对面,甲的右边是丙,左边是丁
D.
甲在丁的对面,乙在甲的右边,丙在丁的右边
5.
如图甲是从(
)面看到的图乙的图形。
6.
一位美术老师在课堂上进行立体模型素描教学时,把14个棱长为1分米的正方体在课桌上摆成如图形式,然后把露出的表面上不同颜色,则被涂上颜色部分的面积为
。
7.
下面图形是由小正方体木块搭成的几何体的三视图示意图,则该几何体的实物图形是什么模样的 它由多少个小正方体木块搭成。请用小木块实地操作一下吧!
8.
画出下面几何体的主视图、左视图与俯视图。
9.
如图是由几个小正方体块所搭几何体的俯视图,小正方体中的数字表示在该位置小立方块的个数。请画出这个几何体的主视图和左视图。
10.
画出下列几何体的三种视图
【试题答案】
1.
C
2.
C
3.
B
4.
D
5.
上
6.
S=33分米2
7.
图略。共7块。
8.
这个几何体的主视图、左视图与俯视图分别是:
9.
10.
(1)
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
