辽宁省凌海市七年级数学下册课后补习班辅导暑假专题—操作型试题(二)讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导暑假专题—操作型试题(二)讲学案苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 08:01:31 | ||
图片预览

文档简介
暑假专题——操作型试题(二)
【本讲教育信息】
一. 教学内容:
暑假专题——操作型试题(二)
4、方案设计
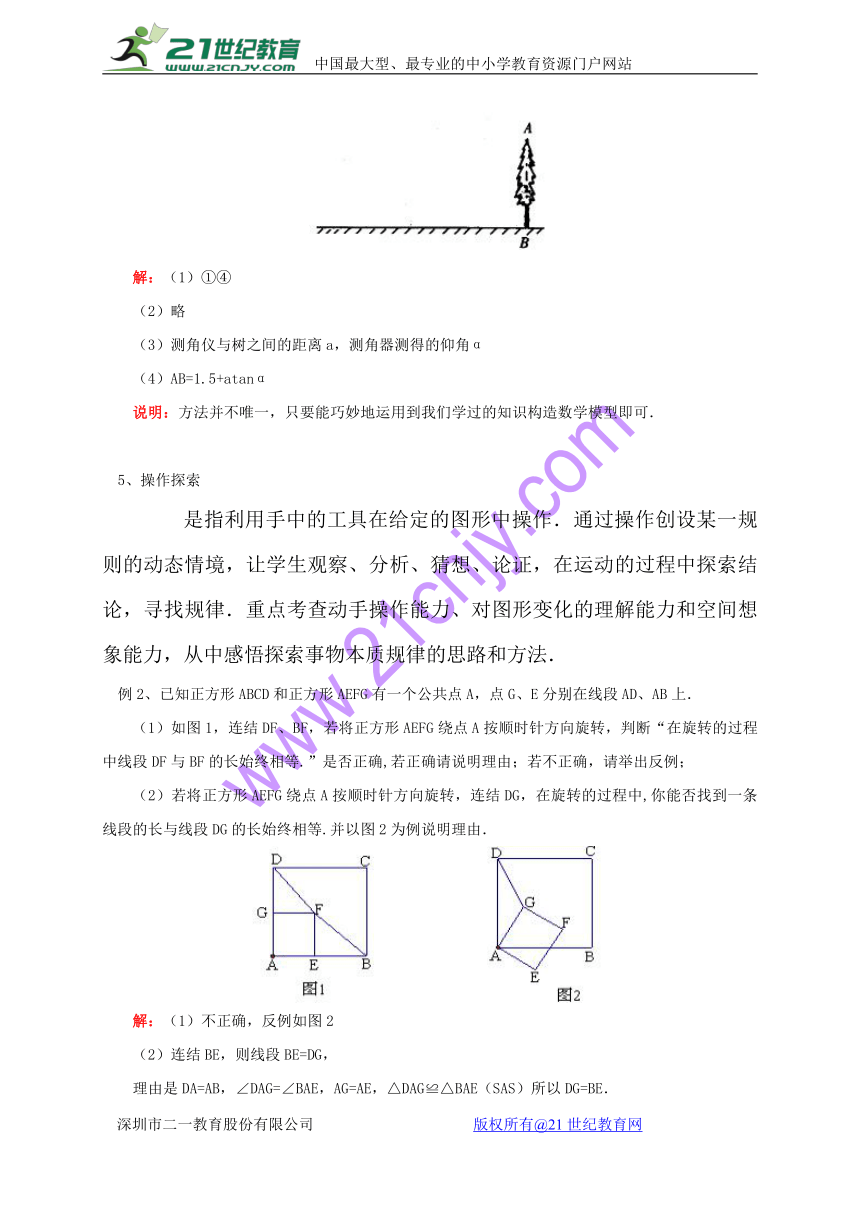
例1、为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
实践一:根据《自然科学》中光的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:
把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度(精确到0.1米).21cnjy.com
解:∵ ∴5.2米
说明:相似三角形对应边成比例.
实践二:提供选用的测量工具有①皮尺一根;②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架.请根据你所设计的测量方案,回答下列问题:www.21-cn-jy.com
(1)在你设计的方案中,选用的测量工具是(用工具的序号填写) ;
(2)在下图中画出你的测量方案示意图;
(3)你需要测得示意图中哪些数据,并分别用a、b、c,α、β等表示测得的数据 ;
(4)写出求树高的算式:AB= .
(提示:在RtΔABC中,)
解:(1)①④
(2)略
(3)测角仪与树之间的距离a,测角器测得的仰角α
(4)AB=1.5+atanα
说明:方法并不唯一,只要能巧妙地运用到我们学过的知识构造数学模型即可.
5、操作探索
是指利用手中的工具在给定的图形中操作.通过操作创设某一规则的动态情境,让学生观察、分析、猜想、论证,在运动的过程中探索结论,寻找规律.重点考查动手操作能力、对图形变化的理解能力和空间想象能力,从中感悟探索事物本质规律的思路和方法.21·cn·jy·com
例2、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1)如图1,连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由;若不正确,请举出反例;
(2)若将正方形AEFG绕点A按顺时针方向旋转,连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.2·1·c·n·j·y
解:(1)不正确,反例如图2
(2)连结BE,则线段BE=DG,
理由是DA=AB,∠DAG=∠BAE,AG=AE,△DAG≌△BAE(SAS)所以DG=BE.
【模拟试题】(答题时间:30分钟)
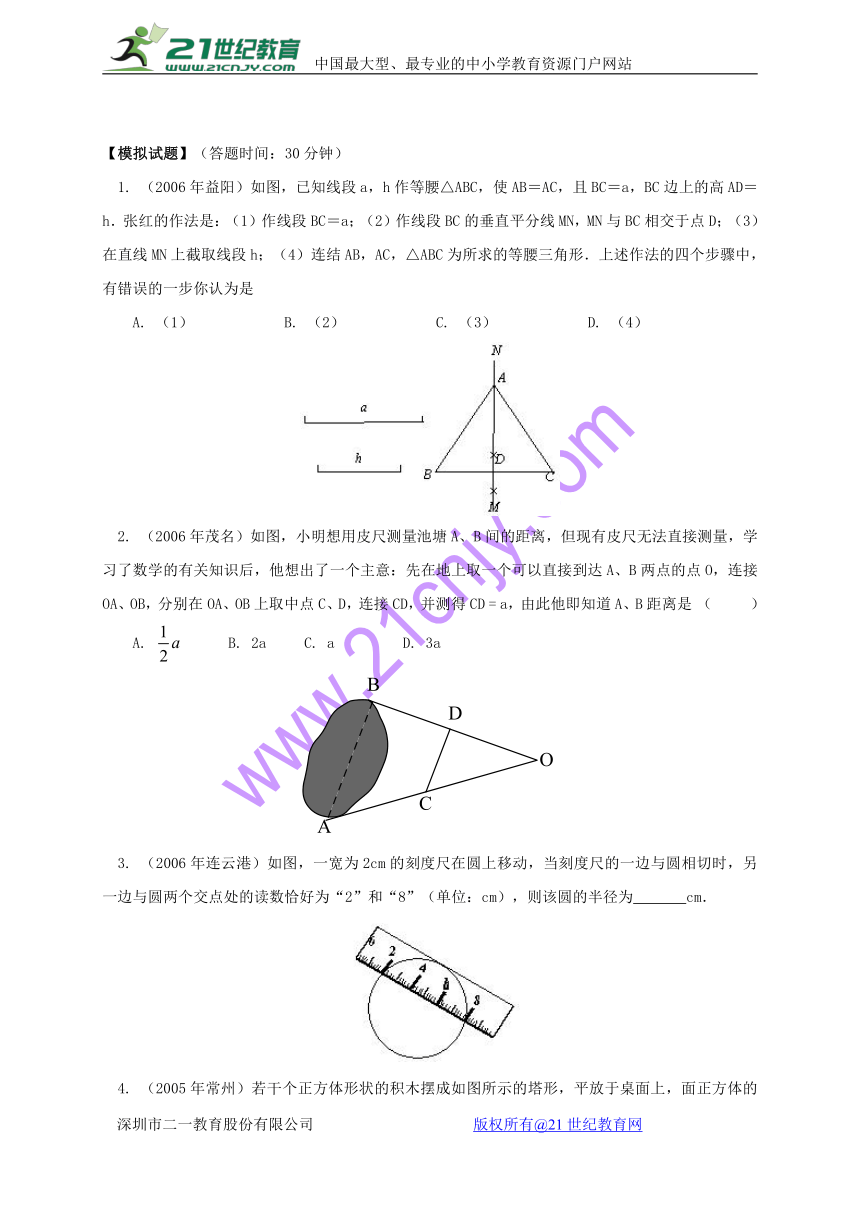
1. (2006年益阳)如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连结AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是【来源:21·世纪·教育·网】
A. (1) B. (2) C. (3) D. (4)
2. (2006年茂名)如图,小明想用皮尺测量池塘A、B间的距离,但现有皮尺无法直接测量,学习了数学的有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD = a,由此他即知道A、B距离是 ( )
A. B. 2a C. a D. 3a
3. (2006年连云港)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.
4. (2005年常州)若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,面正方体的下底的四个顶点是下面相邻正方体的上底的各边中点,最下面的正方体的棱长为1,如果塔形露在外面的面积超过7,则正方体至少有__________个.21教育网
5. (2005年扬州)若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.21·世纪*教育网
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由;
(3)归纳:通过上述操作及探究,请概括出具有一般性的结论(不需要证明).
6. (2005年丽水) 某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.www-2-1-cnjy-com
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(附加题:)(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
【试题答案】
1. C 2.B 3. 4. 3
5. 解:(1)略
(2)探究:四边形EBCF是矩形,而且是黄金矩形
∵四边形AEFD是正方形,∴∠AEF=90° ∴∠BEF=90°,
∵四边形ABCD是矩形 ,∴∠B=∠C =90°
∴∠BEF=∠B=∠C =90°,∴四边形EBCF是矩形
【方法1】设
∴
∴矩形EBCF是黄金矩形.
【方法2】设,
∴
∴矩形EBCF是黄金矩形.
(3)归纳:在黄金矩形内以短边为边作一个正方形后,所得到的另外一个四边形是矩形,而且是黄金矩形(关键词:①另外一个四边形是矩形 ,②是黄金矩形).21世纪教育网版权所有
6. 解:(1)作图工具不限,只要点A、B、C在同一圆周上;
(2)作图工具不限,只要点A、B、C在同一平行四边形的顶点上;
(3)∵r=OB==,
∴S⊙O=r2=≈16.75,
又S平行四边形=2S△ABC=2××42×sin60o=8≈13.86
∵S⊙O > S平行四边形 ∴选择建圆形花坛面积较大
【本讲教育信息】
一. 教学内容:
暑假专题——操作型试题(二)
4、方案设计
例1、为了测量校园内一棵不可攀的树的高度,学校数学应用实践小组做了如下的探索:
实践一:根据《自然科学》中光的反射定律,利用一面镜子和一根皮尺,设计如右示意图的测量方案:
把镜子放在离树(AB)8.7米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2.7米,观察者目高CD=1.6米,请你计算树(AB)的高度(精确到0.1米).21cnjy.com
解:∵ ∴5.2米
说明:相似三角形对应边成比例.
实践二:提供选用的测量工具有①皮尺一根;②教学用三角板一副;③长为2.5米的标杆一根;④高度为1.5米的测角仪(能测量仰角、俯角的仪器)一架.请根据你所设计的测量方案,回答下列问题:www.21-cn-jy.com
(1)在你设计的方案中,选用的测量工具是(用工具的序号填写) ;
(2)在下图中画出你的测量方案示意图;
(3)你需要测得示意图中哪些数据,并分别用a、b、c,α、β等表示测得的数据 ;
(4)写出求树高的算式:AB= .
(提示:在RtΔABC中,)
解:(1)①④
(2)略
(3)测角仪与树之间的距离a,测角器测得的仰角α
(4)AB=1.5+atanα
说明:方法并不唯一,只要能巧妙地运用到我们学过的知识构造数学模型即可.
5、操作探索
是指利用手中的工具在给定的图形中操作.通过操作创设某一规则的动态情境,让学生观察、分析、猜想、论证,在运动的过程中探索结论,寻找规律.重点考查动手操作能力、对图形变化的理解能力和空间想象能力,从中感悟探索事物本质规律的思路和方法.21·cn·jy·com
例2、已知正方形ABCD和正方形AEFG有一个公共点A,点G、E分别在线段AD、AB上.
(1)如图1,连结DF、BF,若将正方形AEFG绕点A按顺时针方向旋转,判断“在旋转的过程中线段DF与BF的长始终相等.”是否正确,若正确请说明理由;若不正确,请举出反例;
(2)若将正方形AEFG绕点A按顺时针方向旋转,连结DG,在旋转的过程中,你能否找到一条线段的长与线段DG的长始终相等.并以图2为例说明理由.2·1·c·n·j·y
解:(1)不正确,反例如图2
(2)连结BE,则线段BE=DG,
理由是DA=AB,∠DAG=∠BAE,AG=AE,△DAG≌△BAE(SAS)所以DG=BE.
【模拟试题】(答题时间:30分钟)
1. (2006年益阳)如图,已知线段a,h作等腰△ABC,使AB=AC,且BC=a,BC边上的高AD=h.张红的作法是:(1)作线段BC=a;(2)作线段BC的垂直平分线MN,MN与BC相交于点D;(3)在直线MN上截取线段h;(4)连结AB,AC,△ABC为所求的等腰三角形.上述作法的四个步骤中,有错误的一步你认为是【来源:21·世纪·教育·网】
A. (1) B. (2) C. (3) D. (4)
2. (2006年茂名)如图,小明想用皮尺测量池塘A、B间的距离,但现有皮尺无法直接测量,学习了数学的有关知识后,他想出了一个主意:先在地上取一个可以直接到达A、B两点的点O,连接OA、OB,分别在OA、OB上取中点C、D,连接CD,并测得CD = a,由此他即知道A、B距离是 ( )
A. B. 2a C. a D. 3a
3. (2006年连云港)如图,一宽为2cm的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm),则该圆的半径为 cm.
4. (2005年常州)若干个正方体形状的积木摆成如图所示的塔形,平放于桌面上,面正方体的下底的四个顶点是下面相邻正方体的上底的各边中点,最下面的正方体的棱长为1,如果塔形露在外面的面积超过7,则正方体至少有__________个.21教育网
5. (2005年扬州)若一个矩形的短边与长边的比值为(黄金分割数),我们把这样的矩形叫做黄金矩形.21·世纪*教育网
(1)操作:请你在如图所示的黄金矩形ABCD(AB>AD)中,以短边AD为一边作正方形AEFD;
(2)探究:在(1)中的四边形EBCF是不是黄金矩形?若是,请予以证明;若不是,请说明理由;
(3)归纳:通过上述操作及探究,请概括出具有一般性的结论(不需要证明).
6. (2005年丽水) 某公园有一个边长为4米的正三角形花坛,三角形的顶点A、B、C上各有一棵古树.现决定把原来的花坛扩建成一个圆形或平行四边形花坛,要求三棵古树不能移动,且三棵古树位于圆周上或平行四边形的顶点上.以下设计过程中画图工具不限.www-2-1-cnjy-com
(1)按圆形设计,利用图1画出你所设计的圆形花坛示意图;
(2)按平行四边形设计,利用图2画出你所设计的平行四边形花坛示意图;
(附加题:)(3)若想新建的花坛面积较大,选择以上哪一种方案合适?请说明理由.
【试题答案】
1. C 2.B 3. 4. 3
5. 解:(1)略
(2)探究:四边形EBCF是矩形,而且是黄金矩形
∵四边形AEFD是正方形,∴∠AEF=90° ∴∠BEF=90°,
∵四边形ABCD是矩形 ,∴∠B=∠C =90°
∴∠BEF=∠B=∠C =90°,∴四边形EBCF是矩形
【方法1】设
∴
∴矩形EBCF是黄金矩形.
【方法2】设,
∴
∴矩形EBCF是黄金矩形.
(3)归纳:在黄金矩形内以短边为边作一个正方形后,所得到的另外一个四边形是矩形,而且是黄金矩形(关键词:①另外一个四边形是矩形 ,②是黄金矩形).21世纪教育网版权所有
6. 解:(1)作图工具不限,只要点A、B、C在同一圆周上;
(2)作图工具不限,只要点A、B、C在同一平行四边形的顶点上;
(3)∵r=OB==,
∴S⊙O=r2=≈16.75,
又S平行四边形=2S△ABC=2××42×sin60o=8≈13.86
∵S⊙O > S平行四边形 ∴选择建圆形花坛面积较大
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
