辽宁省凌海市七年级数学下册课后补习班辅导暑假专题—操作型试题(一)讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导暑假专题—操作型试题(一)讲学案苏科版 |

|
|
| 格式 | zip | ||
| 文件大小 | 304.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 00:00:00 | ||
图片预览

文档简介
暑假专题——操作型试题(一)
【本讲教育信息】
一.
教学内容:
暑假专题——操作型试题(一)
操作型试题是指给出操作规则,在操作过程中发现新结论,自主探索知识的发展过程;它为解题者创设了动手实践,操作设计的空间,考查了数学实践能力和创新设计才能.是近几年全国各地中考命题的热点.
二、知识要点:
1、画图与拼图
它直接考查实际操作能力.这类题大多联系生活实际,内容开放.需要考生进行多方面、多角度、多层次的探索,能检验考生思维的灵活性
、发散性和创新性.
2、折叠与变换
图形的折叠实际上就是全等变换,实质就是轴对称.
解题关键:分清折叠前后哪些量变了、哪些量没有变,折叠后又有哪些条件可以利用.
载体:1)以三角形为载体
2)以矩形为载体
3)以梯形为载体
4)以圆为载体
3、旋转与展开
【典型例题】
例1、在一服装厂里有大量形状为等腰直角三角形的边角布料(如图)
找出其中的一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其它边相切.请设计出所有符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径)
分析:扇形的剪法并不唯一,但只要抓住圆心和半径两点就可以确定下来.一般来说圆心定位,半径定形,所以我们可以先确定圆心的位置.
解:略
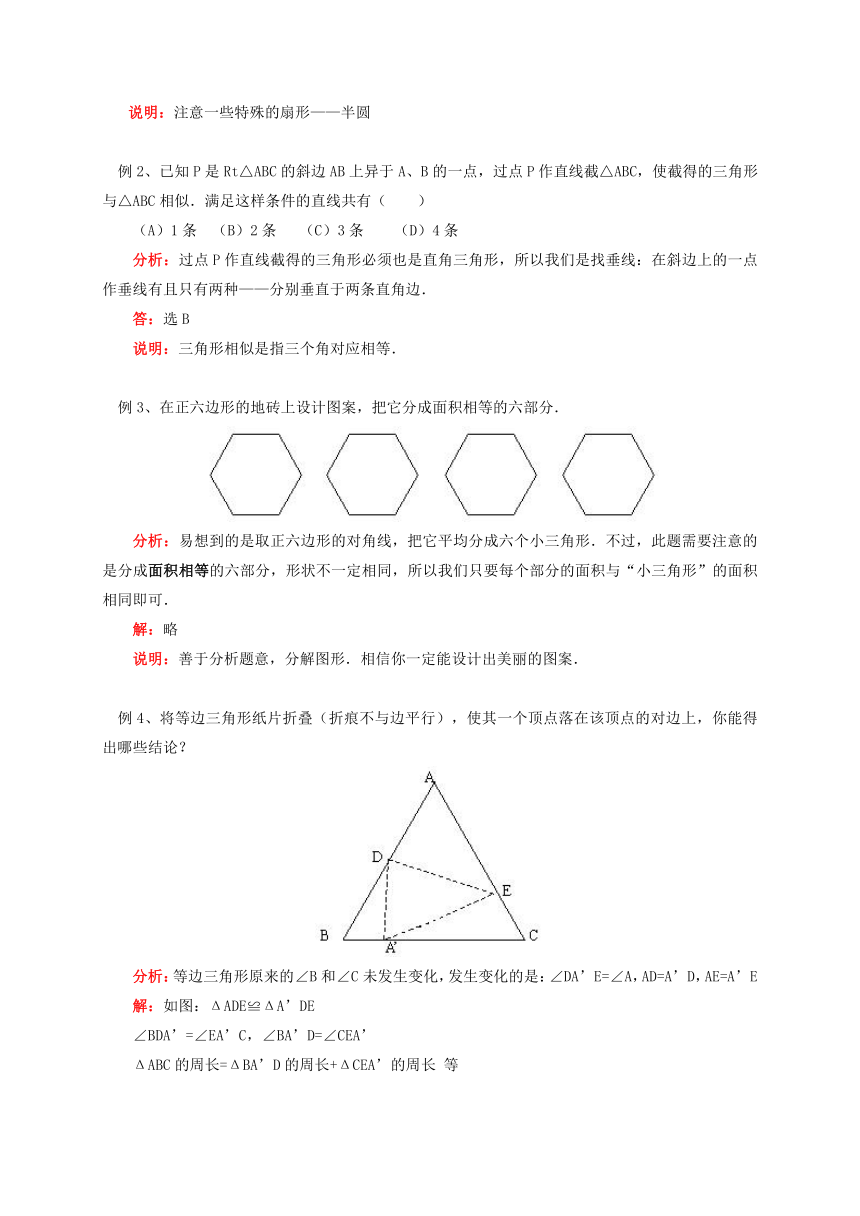
说明:注意一些特殊的扇形——半圆
例2、已知P是Rt△ABC的斜边AB上异于A、B的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似.满足这样条件的直线共有(
)
(A)1条
(B)2条
(C)3条
(D)4条
分析:过点P作直线截得的三角形必须也是直角三角形,所以我们是找垂线:在斜边上的一点作垂线有且只有两种——分别垂直于两条直角边.
答:选B
说明:三角形相似是指三个角对应相等.
例3、在正六边形的地砖上设计图案,把它分成面积相等的六部分.
分析:易想到的是取正六边形的对角线,把它平均分成六个小三角形.不过,此题需要注意的是分成面积相等的六部分,形状不一定相同,所以我们只要每个部分的面积与“小三角形”的面积相同即可.
解:略
说明:善于分析题意,分解图形.相信你一定能设计出美丽的图案.
例4、将等边三角形纸片折叠(折痕不与边平行),使其一个顶点落在该顶点的对边上,你能得出哪些结论?
分析:等边三角形原来的∠B和∠C未发生变化,发生变化的是:∠DA’E=∠A,AD=A’D,AE=A’E
解:如图:ΔADE≌ΔA’DE
∠BDA’=∠EA’C,∠BA’D=∠CEA’
ΔABC的周长=ΔBA’D的周长+ΔCEA’的周长
等
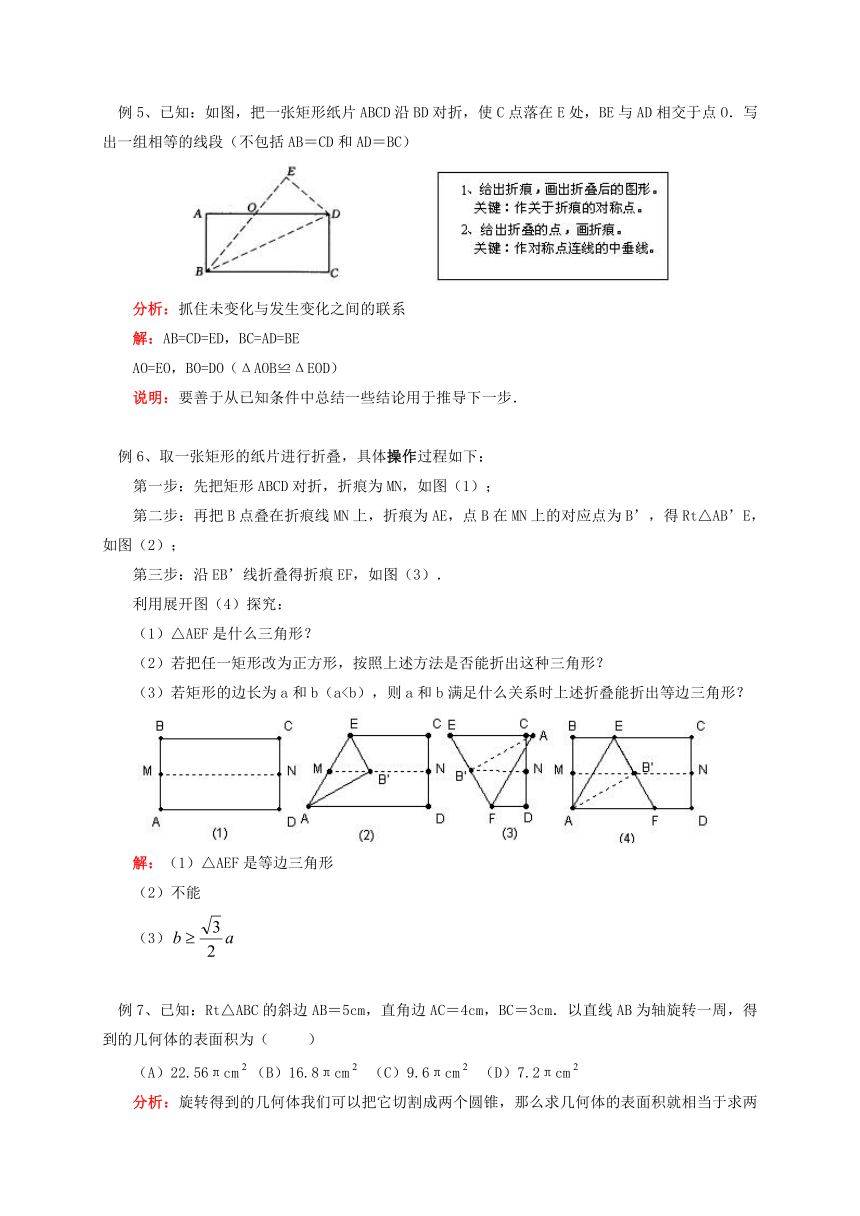
例5、已知:如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O.写出一组相等的线段(不包括AB=CD和AD=BC)
分析:抓住未变化与发生变化之间的联系
解:AB=CD=ED,BC=AD=BE
AO=EO,BO=DO(ΔAOB≌ΔEOD)
说明:要善于从已知条件中总结一些结论用于推导下一步.
例6、取一张矩形的纸片进行折叠,具体操作过程如下:
第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B’,得Rt△AB’E,如图(2);
第三步:沿EB’线折叠得折痕EF,如图(3).
利用展开图(4)探究:
(1)△AEF是什么三角形?
(2)若把任一矩形改为正方形,按照上述方法是否能折出这种三角形?
(3)若矩形的边长为a和b(a解:(1)△AEF是等边三角形
(2)不能
(3)
例7、已知:Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm.以直线AB为轴旋转一周,得到的几何体的表面积为(
)
(A)22.56πcm(B)16.8πcm
(C)9.6πcm
(D)7.2πcm
分析:旋转得到的几何体我们可以把它切割成两个圆锥,那么求几何体的表面积就相当于求两个圆锥的侧面积的和了.
答:选B
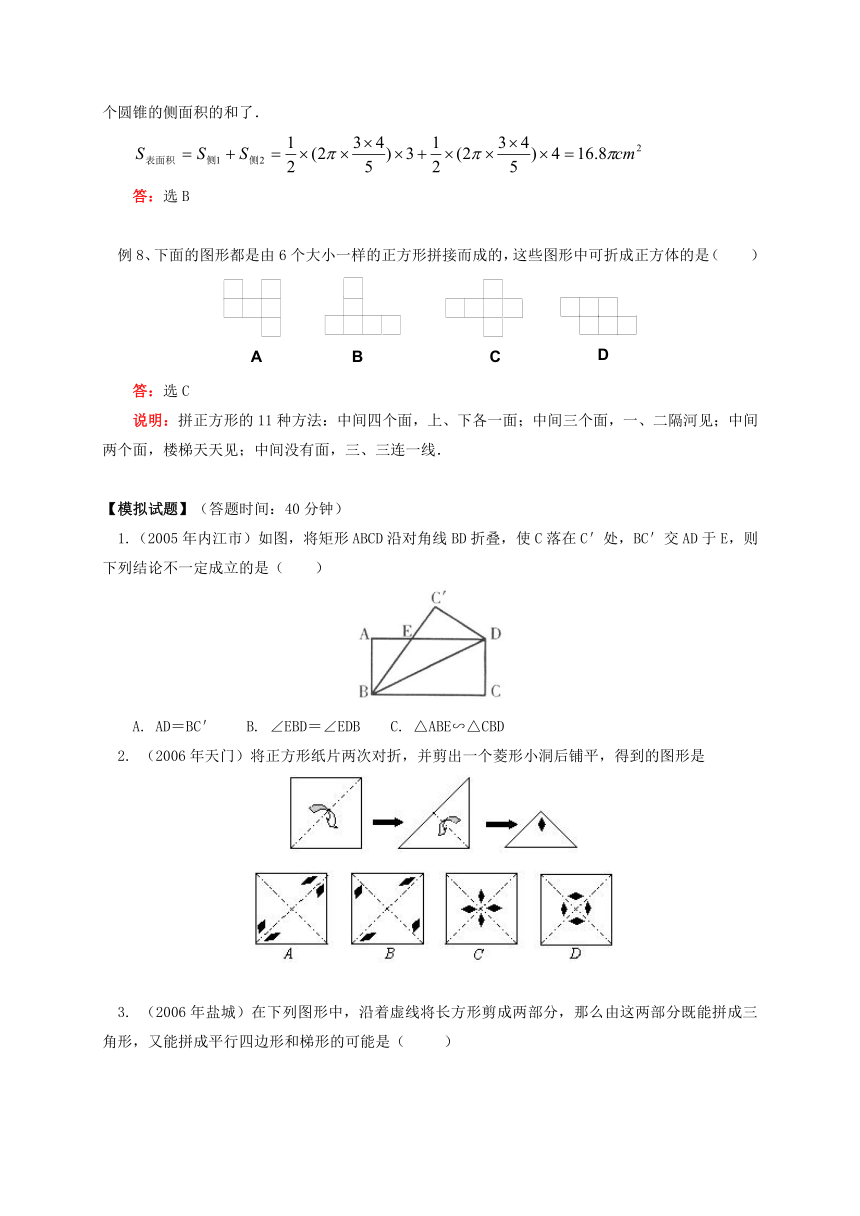
例8、下面的图形都是由6个大小一样的正方形拼接而成的,这些图形中可折成正方体的是(
)
答:选C
说明:拼正方形的11种方法:中间四个面,上、下各一面;中间三个面,一、二隔河见;中间两个面,楼梯天天见;中间没有面,三、三连一线.
【模拟试题】(答题时间:40分钟)
1.(2005年内江市)如图,将矩形ABCD沿对角线BD折叠,使C落在C'处,BC'交AD于E,则下列结论不一定成立的是( )
A.
AD=BC' B.
∠EBD=∠EDB C.
△ABE∽△CBD
2.
(2006年天门)将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是
3.
(2006年盐城)在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形和梯形的可能是(
)
4.
(2006年舟山)如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是
.
5.
(2006年临安)用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=
度.
6.
(2006年永州)如图所示为农村一古老的捣碎器,已知支撑柱的高为
0.3米,踏板长为1.6米,支撑点到踏脚的距离为0.6米,现在踏脚着地,则捣头点上升了_________米.
7.
在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________.
8.
(2006年南昌市)请在由边长为1的小正三角形组成的虚线网格中,画出1
个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形.
9.
(2006年浙江)现有一张长和宽之比为2:1的长方形纸片,将它折两次(第一次折后也可打开铺平再折者第二次),使得折痕将纸片分为面积相等且不重叠的四个部分(称为一次操作),如图甲(虚线表示折痕).除图甲外,请你再给出三种不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作,如图乙和图甲是相同的操作).
甲
乙
①
②
③
10.
(2006年伊春)
如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为l,旋转后点A的对应点依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽的图案能够说明一个著名结论的正确性,请写出这个结论.
附加题:11.
(2006年天津)如图,已知四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到:__________(用“能”或“不能”填空).若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
____________________________________________________________________________
____________________________________________________________________________
_____________________________________________________________________________
【试题答案】
1.
C
2.
C
3.
C
4.
三角形的稳定性
5.
36
6.
0.8
7.
4
8.
本题答案不惟一,只要符合要求都给满分,以下答案供参考
9.
10.
(1)如图,正确画出图案
(2)如图,=-
=(3+5)2-4××3×5
=34
故四边形AA1A2A3的面积为34.
(3)结论:AB2+BC2=AC2或勾股定理的文字叙述.
11.
如图,取四边形ABCD各边的中点E、F、G、H,连结EF、GH,则EF、GH为裁剪线,EF、GH将四边形ABCD分成1、2、3、4个部分,拼接时,图中的标号1不动,将标号2、4分别绕点G、F各旋转180°,标号3平移,拼成的四边形满足条件.
【本讲教育信息】
一.
教学内容:
暑假专题——操作型试题(一)
操作型试题是指给出操作规则,在操作过程中发现新结论,自主探索知识的发展过程;它为解题者创设了动手实践,操作设计的空间,考查了数学实践能力和创新设计才能.是近几年全国各地中考命题的热点.
二、知识要点:
1、画图与拼图
它直接考查实际操作能力.这类题大多联系生活实际,内容开放.需要考生进行多方面、多角度、多层次的探索,能检验考生思维的灵活性
、发散性和创新性.
2、折叠与变换
图形的折叠实际上就是全等变换,实质就是轴对称.
解题关键:分清折叠前后哪些量变了、哪些量没有变,折叠后又有哪些条件可以利用.
载体:1)以三角形为载体
2)以矩形为载体
3)以梯形为载体
4)以圆为载体
3、旋转与展开
【典型例题】
例1、在一服装厂里有大量形状为等腰直角三角形的边角布料(如图)
找出其中的一种,测得∠C=90°,AC=BC=4,今要从这种三角形中剪出一种扇形,做成不同形状的玩具,使扇形的边缘半径恰好都在△ABC的边上,且扇形的弧与△ABC的其它边相切.请设计出所有符合题意的方案示意图,并求出扇形的半径(只要求画出图形,并直接写出扇形半径)
分析:扇形的剪法并不唯一,但只要抓住圆心和半径两点就可以确定下来.一般来说圆心定位,半径定形,所以我们可以先确定圆心的位置.
解:略
说明:注意一些特殊的扇形——半圆
例2、已知P是Rt△ABC的斜边AB上异于A、B的一点,过点P作直线截△ABC,使截得的三角形与△ABC相似.满足这样条件的直线共有(
)
(A)1条
(B)2条
(C)3条
(D)4条
分析:过点P作直线截得的三角形必须也是直角三角形,所以我们是找垂线:在斜边上的一点作垂线有且只有两种——分别垂直于两条直角边.
答:选B
说明:三角形相似是指三个角对应相等.
例3、在正六边形的地砖上设计图案,把它分成面积相等的六部分.
分析:易想到的是取正六边形的对角线,把它平均分成六个小三角形.不过,此题需要注意的是分成面积相等的六部分,形状不一定相同,所以我们只要每个部分的面积与“小三角形”的面积相同即可.
解:略
说明:善于分析题意,分解图形.相信你一定能设计出美丽的图案.
例4、将等边三角形纸片折叠(折痕不与边平行),使其一个顶点落在该顶点的对边上,你能得出哪些结论?
分析:等边三角形原来的∠B和∠C未发生变化,发生变化的是:∠DA’E=∠A,AD=A’D,AE=A’E
解:如图:ΔADE≌ΔA’DE
∠BDA’=∠EA’C,∠BA’D=∠CEA’
ΔABC的周长=ΔBA’D的周长+ΔCEA’的周长
等
例5、已知:如图,把一张矩形纸片ABCD沿BD对折,使C点落在E处,BE与AD相交于点O.写出一组相等的线段(不包括AB=CD和AD=BC)
分析:抓住未变化与发生变化之间的联系
解:AB=CD=ED,BC=AD=BE
AO=EO,BO=DO(ΔAOB≌ΔEOD)
说明:要善于从已知条件中总结一些结论用于推导下一步.
例6、取一张矩形的纸片进行折叠,具体操作过程如下:
第一步:先把矩形ABCD对折,折痕为MN,如图(1);
第二步:再把B点叠在折痕线MN上,折痕为AE,点B在MN上的对应点为B’,得Rt△AB’E,如图(2);
第三步:沿EB’线折叠得折痕EF,如图(3).
利用展开图(4)探究:
(1)△AEF是什么三角形?
(2)若把任一矩形改为正方形,按照上述方法是否能折出这种三角形?
(3)若矩形的边长为a和b(a
(2)不能
(3)
例7、已知:Rt△ABC的斜边AB=5cm,直角边AC=4cm,BC=3cm.以直线AB为轴旋转一周,得到的几何体的表面积为(
)
(A)22.56πcm(B)16.8πcm
(C)9.6πcm
(D)7.2πcm
分析:旋转得到的几何体我们可以把它切割成两个圆锥,那么求几何体的表面积就相当于求两个圆锥的侧面积的和了.
答:选B
例8、下面的图形都是由6个大小一样的正方形拼接而成的,这些图形中可折成正方体的是(
)
答:选C
说明:拼正方形的11种方法:中间四个面,上、下各一面;中间三个面,一、二隔河见;中间两个面,楼梯天天见;中间没有面,三、三连一线.
【模拟试题】(答题时间:40分钟)
1.(2005年内江市)如图,将矩形ABCD沿对角线BD折叠,使C落在C'处,BC'交AD于E,则下列结论不一定成立的是( )
A.
AD=BC' B.
∠EBD=∠EDB C.
△ABE∽△CBD
2.
(2006年天门)将正方形纸片两次对折,并剪出一个菱形小洞后铺平,得到的图形是
3.
(2006年盐城)在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形和梯形的可能是(
)
4.
(2006年舟山)如图,一扇窗户打开后,用窗钩BC可将其固定,这里所运用的几何原理是
.
5.
(2006年临安)用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC=
度.
6.
(2006年永州)如图所示为农村一古老的捣碎器,已知支撑柱的高为
0.3米,踏板长为1.6米,支撑点到踏脚的距离为0.6米,现在踏脚着地,则捣头点上升了_________米.
7.
在直线l上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积分别是1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+S2+S3+S4=_________.
8.
(2006年南昌市)请在由边长为1的小正三角形组成的虚线网格中,画出1
个所有顶点均在格点上,且至少有一条边为无理数的等腰三角形.
9.
(2006年浙江)现有一张长和宽之比为2:1的长方形纸片,将它折两次(第一次折后也可打开铺平再折者第二次),使得折痕将纸片分为面积相等且不重叠的四个部分(称为一次操作),如图甲(虚线表示折痕).除图甲外,请你再给出三种不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作,如图乙和图甲是相同的操作).
甲
乙
①
②
③
10.
(2006年伊春)
如图,在网格中有一个四边形图案.
(1)请你画出此图案绕点O顺时针方向旋转90°,180°,270°的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错;
(2)若网格中每个小正方形的边长为l,旋转后点A的对应点依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽的图案能够说明一个著名结论的正确性,请写出这个结论.
附加题:11.
(2006年天津)如图,已知四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线最多有两条,能否做到:__________(用“能”或“不能”填空).若填“能”,请确定裁剪线的位置,并说明拼接方法;若填“不能”,请简要说明理由.
____________________________________________________________________________
____________________________________________________________________________
_____________________________________________________________________________
【试题答案】
1.
C
2.
C
3.
C
4.
三角形的稳定性
5.
36
6.
0.8
7.
4
8.
本题答案不惟一,只要符合要求都给满分,以下答案供参考
9.
10.
(1)如图,正确画出图案
(2)如图,=-
=(3+5)2-4××3×5
=34
故四边形AA1A2A3的面积为34.
(3)结论:AB2+BC2=AC2或勾股定理的文字叙述.
11.
如图,取四边形ABCD各边的中点E、F、G、H,连结EF、GH,则EF、GH为裁剪线,EF、GH将四边形ABCD分成1、2、3、4个部分,拼接时,图中的标号1不动,将标号2、4分别绕点G、F各旋转180°,标号3平移,拼成的四边形满足条件.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
