辽宁省凌海市七年级数学下册课后补习班辅导图形的平移与认识三角形讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导图形的平移与认识三角形讲学案苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 376.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 08:08:53 | ||
图片预览



文档简介
图形的平移与认识三角形
【本讲教育信息】
一.
教学内容:
图形的平移与认识三角形
[目标]
1.
知道平移不改变图形的形状、大小
2.
理解图形经过平移,连接各组对应点得线段平行(或在同一直线上)并且相等。
3.
掌握三角形的有关概念,及构成三角形的条件
4.
理解三角形的角平分线、中线和高等几个概念,并会正确画出任意一个三角形的角平分线、中线和高。
二.
重、难点:
1.
理解平移不改变图形的形状、大小
2.
图形平移性质与平行线之间距离的理解与运用
3.
构成三角形的条件及其应用
4.
三角形的角平分线、中线和高的概念及其画法
三.
知识要点
1.
图形的平移:
(1)概念:
在平面内,将一个图形沿着某个方向移动一定的距离,叫做图形的平移。
(2)特点:
①不改变图形的形状、大小,只改变图形的位置;
②图形对应线段、对应点所连的线段平行且相等
说明:如何进行图形的平移:看清方向、距离(找出对应点并连接)
(3)如果两条直线互相平行,那么其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离。
2.
三角形:
(1)由不在同一直线上的三条线段,首尾顺次相接组成的图形。
记作:△ABC
三角形的顶点:A、B、C
三角形的内角:∠A、∠B、∠C
三角形的边:AB、AC、BC
(2)三角形的分类
①按角分类
②按边分类
所有内角都是锐角的三角形——锐角三角形——
有一个内角是直角的三角形——直角三角形——
有一个内角是钝角的三角形——钝角三角形——
(3)三角形的三边关系:
任意两边之和大于第三边;任意两边之差小于第三边。
即第三边大于两边之差,小于两边之和。
(4)三角形的特殊线段:
a)三角形的高:
在三角形中,从一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高。如图(1),线段AD垂直BC,垂足为D,我们把线段AD叫做△ABC中BC边上的高
b)三角形的角平分线:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。如图(2),线段AE平分∠BAC交边BC于点E,我们把线段AE叫做△ABC
中∠BAC的角平分线
c)三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。如图(3),F是△ABC边BC上的中点,我们把线段AF叫做△ABC
中BC边上的中线。
d)
三角形的中线
三条中线交于三角形内一点
三角形的角平分线
三条角平分线交于三角形内一点
三角形的高
锐角三角形的三条高交于三角形内一点;直角三角形的三条高交于边上;钝角三角形的三条高交于三角形外一点
【典型例题】
例1.
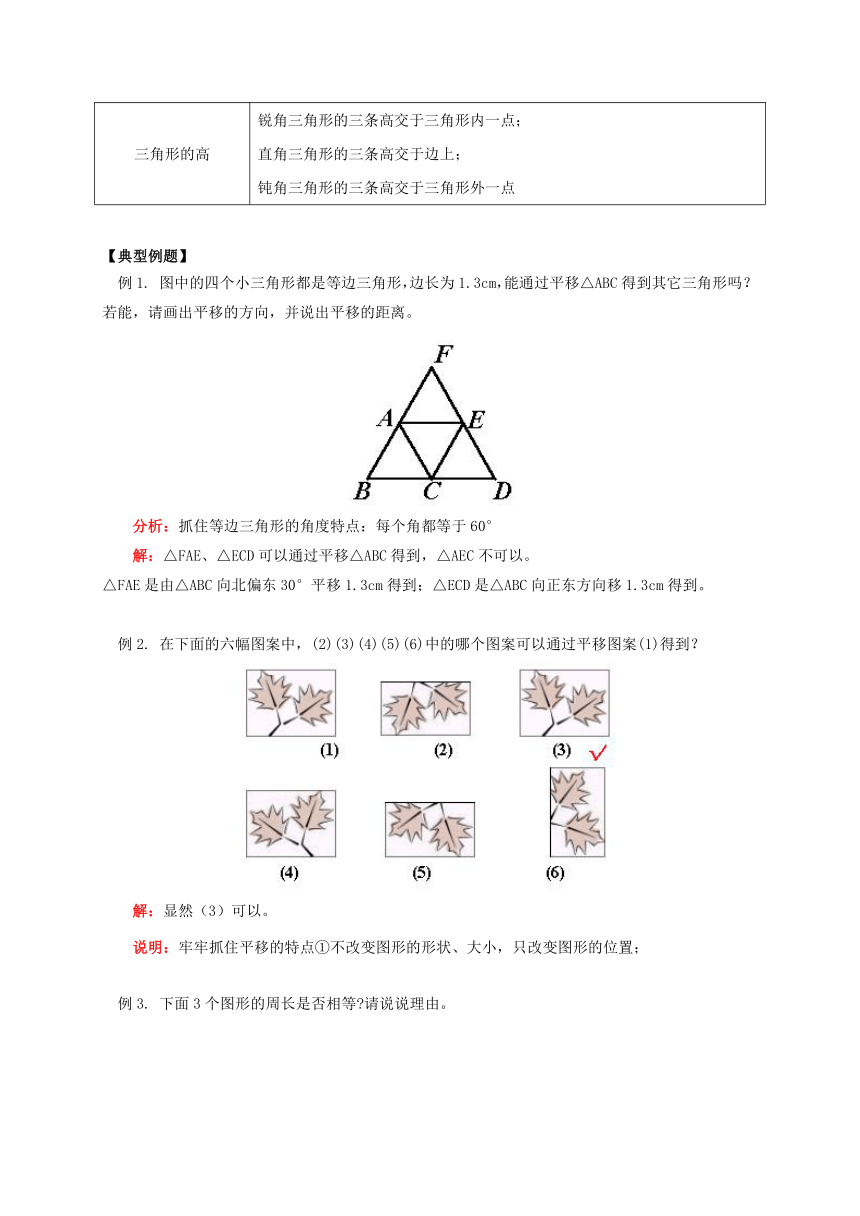
图中的四个小三角形都是等边三角形,边长为1.3cm,能通过平移△ABC得到其它三角形吗?若能,请画出平移的方向,并说出平移的距离。
分析:抓住等边三角形的角度特点:每个角都等于60°
解:△FAE、△ECD可以通过平移△ABC得到,△AEC不可以。
△FAE是由△ABC向北偏东30°平移1.3cm得到;△ECD是△ABC向正东方向移1.3cm得到。
例2.
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
解:显然(3)可以。
说明:牢牢抓住平移的特点①不改变图形的形状、大小,只改变图形的位置;
例3.
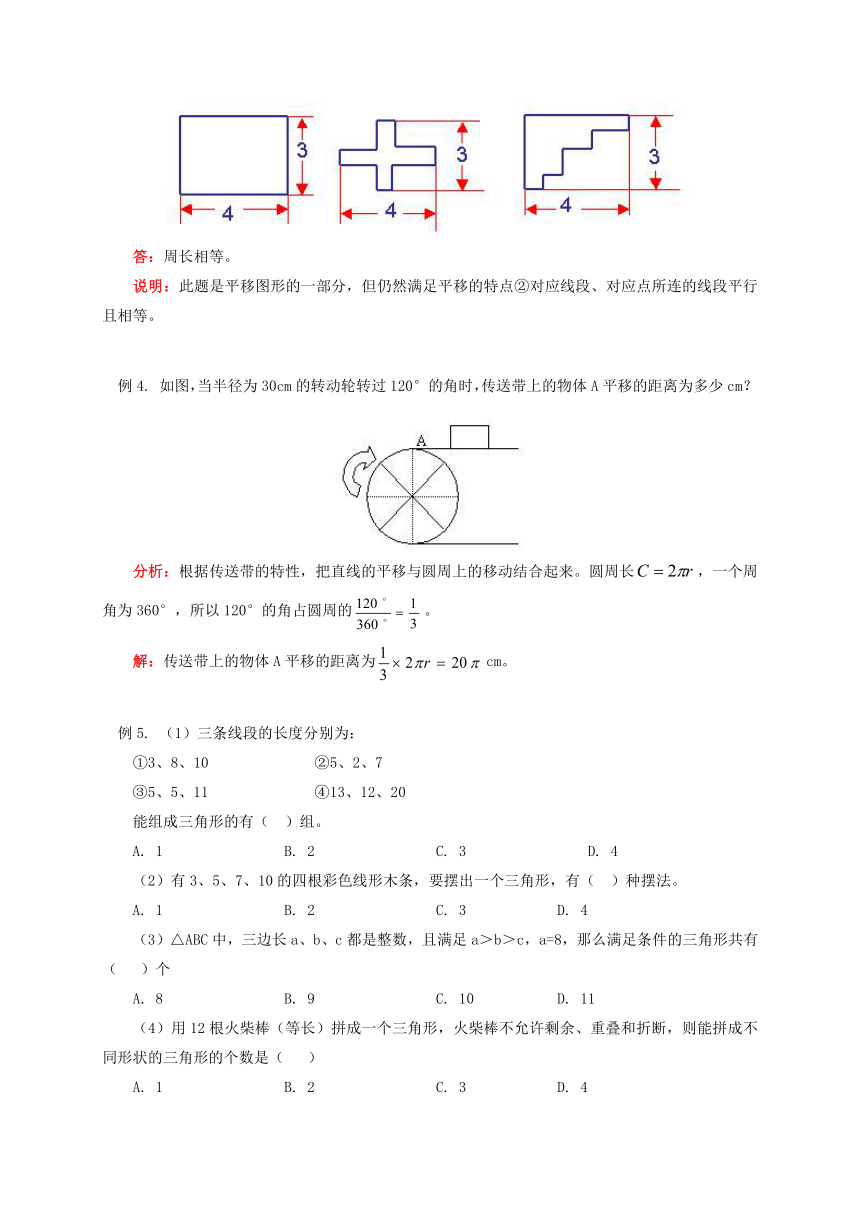
下面3个图形的周长是否相等 请说说理由。
答:周长相等。
说明:此题是平移图形的一部分,但仍然满足平移的特点②对应线段、对应点所连的线段平行且相等。
例4.
如图,当半径为30cm的转动轮转过120°的角时,传送带上的物体A平移的距离为多少cm?
分析:根据传送带的特性,把直线的平移与圆周上的移动结合起来。圆周长,一个周角为360°,所以120°的角占圆周的。
解:传送带上的物体A平移的距离为cm。
例5.
(1)三条线段的长度分别为:
①3、8、10
②5、2、7
③5、5、11
④13、12、20
能组成三角形的有(
)组。
A.
1
B.
2
C.
3
D.
4
(2)有3、5、7、10的四根彩色线形木条,要摆出一个三角形,有(
)种摆法。
A.
1
B.
2
C.
3
D.
4
(3)△ABC中,三边长a、b、c都是整数,且满足a>b>c,a=8,那么满足条件的三角形共有(
)个
A.
8
B.
9
C.
10
D.
11
(4)用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能拼成不同形状的三角形的个数是(
)
A.
1
B.
2
C.
3
D.
4
分析:(1)(2)抓住任意的“第三边”大于两边之差,小于两边之和。(3)(4)均要结合正整数去考虑。特别是(4)已知的是三角形的周长。
答:(1)B
(2)B
(3)B
(4)C
说明:(1)中②5+2=7,③5+5=10<11均不满足两边之和大于第三边
(2)有3,5,7;5,7,10两组。
(3)有8,
7,6;8,7,5;8,7,4;8,7,3;8,7,2;8,6,5;8,6,4;8,6,3;8,5,4九组。
(4)5,5,2;5,4,3;
4,4,4三组
例6.
(1)已知一个三角形的三边长为3、8、x,则x
的取值范围是
。
(2)已知一个三角形的三边长为3、a+2、8,则a的取值范围是
。
(3)一个三角形的两边长是3、5,则它周长C的范围是
。
(4)等腰三角形一边的长是5,另一边的长是8,则它的周长是
。
分析:(1)(2)(3)紧扣“三角形两边之和大于第三边,两边之差小于第三边”。(4)根据等腰三角形的特点去分类,但要验证结果是否满足三角形三边的关系。
解:(1)5例7.
如图,CM是△ABC的中线,已知△AMC的周长比△BMC的周长大3,求AC与BC的差。
分析:本题很容易,关键在于抓住三角形中线的定义。
解:△AMC的周长=AC+CM+AM,△BMC的周长=BC+CM+BM
∵CM是△ABC的中线
∴AM=BM,又CM=CM
∴△AMC的周长-△BMC的周长=AC-BC=3
答:AC与BC的差为3。
例8.
如图,已知D、E分别是△ABC的边AB、BC的中点,
(1)若△ABC的面积是80,求△DBE的面积;
(2)若DF是△DBE的中线,求△DEF的面积。
解:(1),
而由D、E分别是△ABC的边AB、BC的中点知:,
∴
(2),
∵DF是△DBE的中线,∴
∴
说明:
例9.
如图,AD、CE是△ABC的高,AB=2BC,试问AD
与CE有着怎样的数量关系?为什么?
分析:要想建立AD
与CE的数量关系,又已知高,我们可以从面积入手。
解:
又∵AB=2BC,∴AD=2CE
说明:这种以面积为桥梁建立数量关系的方法称为等面积法。
【模拟试题】(答题时间:40分钟)
1.
已知三角形的两边a=3,b=7,第三边是c,且a)
A.
4B.
7C.
4D.
72.
以下列各组线段长为边,能组成三角形的是(
)
A.
1cm,2cm,4cm
B.
8cm,6cm,4cm
C.
12cm,5cm,6cm
D.
2cm,3cm,6cm
3.
以下现象属于平移的是(
)
①小船在波浪上航行
②钟摆的摆动
③传送带上饮料的移动
④用打气筒打气时活塞的移动
A.
①②
B.
①③
C.
③④
D.
②④
4.
将线段AB先向右平移3cm,再向上平移2cm,再向下平移3cm,再向上平移1cm,最后得到的线段怎样由AB直接平移得到(
)
A.
向左平移2cm
B.
向上平移1cm
C.
向右平移3cm
D.
原地不动
5.
平移下图中的图案,能得到下列哪一个图案(
)
A.
B.
C.
D.
6.
三角形的角平分线、中线、高都是(
)
A.
直线
B.
线段
C.
射线
D.
以上都不对
7.
一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为(
)
A.
10
B.
12
C.
14
D.
16
8.
设a,b,c是△ABC的三边长,化简|a+b-c|+|b+c-a|+|c+a-b|=__________
9.
在一个三角形中,锐角最多有______个,钝角最多有_______个.
10.
已知△ABC的周长为18cm,AB边比AC边短2cm,BC边是AC边的一半,则AB=
,BC=
,CA=
。
11.
(1)作出△ABC的三条高
(2)将下图按箭头方向平移3cm
12.
如图,请计算图中共有多少个三角形
【试题答案】
1.
B
2.
B
3.
C
4.
C
5.
B
6.
B
7.
C
8.
a+b+c
9.
3;1
10.
6cm;4cm;8cm
11.
图略
12.
35
【图片欣赏】
这些都是通过平移变换来的图像,漂亮吗?你可以自己动手做一做。
【本讲教育信息】
一.
教学内容:
图形的平移与认识三角形
[目标]
1.
知道平移不改变图形的形状、大小
2.
理解图形经过平移,连接各组对应点得线段平行(或在同一直线上)并且相等。
3.
掌握三角形的有关概念,及构成三角形的条件
4.
理解三角形的角平分线、中线和高等几个概念,并会正确画出任意一个三角形的角平分线、中线和高。
二.
重、难点:
1.
理解平移不改变图形的形状、大小
2.
图形平移性质与平行线之间距离的理解与运用
3.
构成三角形的条件及其应用
4.
三角形的角平分线、中线和高的概念及其画法
三.
知识要点
1.
图形的平移:
(1)概念:
在平面内,将一个图形沿着某个方向移动一定的距离,叫做图形的平移。
(2)特点:
①不改变图形的形状、大小,只改变图形的位置;
②图形对应线段、对应点所连的线段平行且相等
说明:如何进行图形的平移:看清方向、距离(找出对应点并连接)
(3)如果两条直线互相平行,那么其中一条直线上任意两点到另一条直线的距离相等,这个距离称为平行线之间的距离。
2.
三角形:
(1)由不在同一直线上的三条线段,首尾顺次相接组成的图形。
记作:△ABC
三角形的顶点:A、B、C
三角形的内角:∠A、∠B、∠C
三角形的边:AB、AC、BC
(2)三角形的分类
①按角分类
②按边分类
所有内角都是锐角的三角形——锐角三角形——
有一个内角是直角的三角形——直角三角形——
有一个内角是钝角的三角形——钝角三角形——
(3)三角形的三边关系:
任意两边之和大于第三边;任意两边之差小于第三边。
即第三边大于两边之差,小于两边之和。
(4)三角形的特殊线段:
a)三角形的高:
在三角形中,从一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高线,简称三角形的高。如图(1),线段AD垂直BC,垂足为D,我们把线段AD叫做△ABC中BC边上的高
b)三角形的角平分线:
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。如图(2),线段AE平分∠BAC交边BC于点E,我们把线段AE叫做△ABC
中∠BAC的角平分线
c)三角形的中线:
在三角形中,连接一个顶点与它对边中点的线段,叫做三角形的中线。如图(3),F是△ABC边BC上的中点,我们把线段AF叫做△ABC
中BC边上的中线。
d)
三角形的中线
三条中线交于三角形内一点
三角形的角平分线
三条角平分线交于三角形内一点
三角形的高
锐角三角形的三条高交于三角形内一点;直角三角形的三条高交于边上;钝角三角形的三条高交于三角形外一点
【典型例题】
例1.
图中的四个小三角形都是等边三角形,边长为1.3cm,能通过平移△ABC得到其它三角形吗?若能,请画出平移的方向,并说出平移的距离。
分析:抓住等边三角形的角度特点:每个角都等于60°
解:△FAE、△ECD可以通过平移△ABC得到,△AEC不可以。
△FAE是由△ABC向北偏东30°平移1.3cm得到;△ECD是△ABC向正东方向移1.3cm得到。
例2.
在下面的六幅图案中,(2)(3)(4)(5)(6)中的哪个图案可以通过平移图案(1)得到?
解:显然(3)可以。
说明:牢牢抓住平移的特点①不改变图形的形状、大小,只改变图形的位置;
例3.
下面3个图形的周长是否相等 请说说理由。
答:周长相等。
说明:此题是平移图形的一部分,但仍然满足平移的特点②对应线段、对应点所连的线段平行且相等。
例4.
如图,当半径为30cm的转动轮转过120°的角时,传送带上的物体A平移的距离为多少cm?
分析:根据传送带的特性,把直线的平移与圆周上的移动结合起来。圆周长,一个周角为360°,所以120°的角占圆周的。
解:传送带上的物体A平移的距离为cm。
例5.
(1)三条线段的长度分别为:
①3、8、10
②5、2、7
③5、5、11
④13、12、20
能组成三角形的有(
)组。
A.
1
B.
2
C.
3
D.
4
(2)有3、5、7、10的四根彩色线形木条,要摆出一个三角形,有(
)种摆法。
A.
1
B.
2
C.
3
D.
4
(3)△ABC中,三边长a、b、c都是整数,且满足a>b>c,a=8,那么满足条件的三角形共有(
)个
A.
8
B.
9
C.
10
D.
11
(4)用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、重叠和折断,则能拼成不同形状的三角形的个数是(
)
A.
1
B.
2
C.
3
D.
4
分析:(1)(2)抓住任意的“第三边”大于两边之差,小于两边之和。(3)(4)均要结合正整数去考虑。特别是(4)已知的是三角形的周长。
答:(1)B
(2)B
(3)B
(4)C
说明:(1)中②5+2=7,③5+5=10<11均不满足两边之和大于第三边
(2)有3,5,7;5,7,10两组。
(3)有8,
7,6;8,7,5;8,7,4;8,7,3;8,7,2;8,6,5;8,6,4;8,6,3;8,5,4九组。
(4)5,5,2;5,4,3;
4,4,4三组
例6.
(1)已知一个三角形的三边长为3、8、x,则x
的取值范围是
。
(2)已知一个三角形的三边长为3、a+2、8,则a的取值范围是
。
(3)一个三角形的两边长是3、5,则它周长C的范围是
。
(4)等腰三角形一边的长是5,另一边的长是8,则它的周长是
。
分析:(1)(2)(3)紧扣“三角形两边之和大于第三边,两边之差小于第三边”。(4)根据等腰三角形的特点去分类,但要验证结果是否满足三角形三边的关系。
解:(1)5
如图,CM是△ABC的中线,已知△AMC的周长比△BMC的周长大3,求AC与BC的差。
分析:本题很容易,关键在于抓住三角形中线的定义。
解:△AMC的周长=AC+CM+AM,△BMC的周长=BC+CM+BM
∵CM是△ABC的中线
∴AM=BM,又CM=CM
∴△AMC的周长-△BMC的周长=AC-BC=3
答:AC与BC的差为3。
例8.
如图,已知D、E分别是△ABC的边AB、BC的中点,
(1)若△ABC的面积是80,求△DBE的面积;
(2)若DF是△DBE的中线,求△DEF的面积。
解:(1),
而由D、E分别是△ABC的边AB、BC的中点知:,
∴
(2),
∵DF是△DBE的中线,∴
∴
说明:
例9.
如图,AD、CE是△ABC的高,AB=2BC,试问AD
与CE有着怎样的数量关系?为什么?
分析:要想建立AD
与CE的数量关系,又已知高,我们可以从面积入手。
解:
又∵AB=2BC,∴AD=2CE
说明:这种以面积为桥梁建立数量关系的方法称为等面积法。
【模拟试题】(答题时间:40分钟)
1.
已知三角形的两边a=3,b=7,第三边是c,且a
A.
4
7
4
7
以下列各组线段长为边,能组成三角形的是(
)
A.
1cm,2cm,4cm
B.
8cm,6cm,4cm
C.
12cm,5cm,6cm
D.
2cm,3cm,6cm
3.
以下现象属于平移的是(
)
①小船在波浪上航行
②钟摆的摆动
③传送带上饮料的移动
④用打气筒打气时活塞的移动
A.
①②
B.
①③
C.
③④
D.
②④
4.
将线段AB先向右平移3cm,再向上平移2cm,再向下平移3cm,再向上平移1cm,最后得到的线段怎样由AB直接平移得到(
)
A.
向左平移2cm
B.
向上平移1cm
C.
向右平移3cm
D.
原地不动
5.
平移下图中的图案,能得到下列哪一个图案(
)
A.
B.
C.
D.
6.
三角形的角平分线、中线、高都是(
)
A.
直线
B.
线段
C.
射线
D.
以上都不对
7.
一个三角形的两边长为2和6,第三边为偶数,则这个三角形的周长为(
)
A.
10
B.
12
C.
14
D.
16
8.
设a,b,c是△ABC的三边长,化简|a+b-c|+|b+c-a|+|c+a-b|=__________
9.
在一个三角形中,锐角最多有______个,钝角最多有_______个.
10.
已知△ABC的周长为18cm,AB边比AC边短2cm,BC边是AC边的一半,则AB=
,BC=
,CA=
。
11.
(1)作出△ABC的三条高
(2)将下图按箭头方向平移3cm
12.
如图,请计算图中共有多少个三角形
【试题答案】
1.
B
2.
B
3.
C
4.
C
5.
B
6.
B
7.
C
8.
a+b+c
9.
3;1
10.
6cm;4cm;8cm
11.
图略
12.
35
【图片欣赏】
这些都是通过平移变换来的图像,漂亮吗?你可以自己动手做一做。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
