辽宁省凌海市七年级数学下册课后补习班辅导有理数的混合运算—简便运算技巧(2)讲学案苏科版
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导有理数的混合运算—简便运算技巧(2)讲学案苏科版 |  | |
| 格式 | zip | ||
| 文件大小 | 150.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 08:27:52 | ||
图片预览

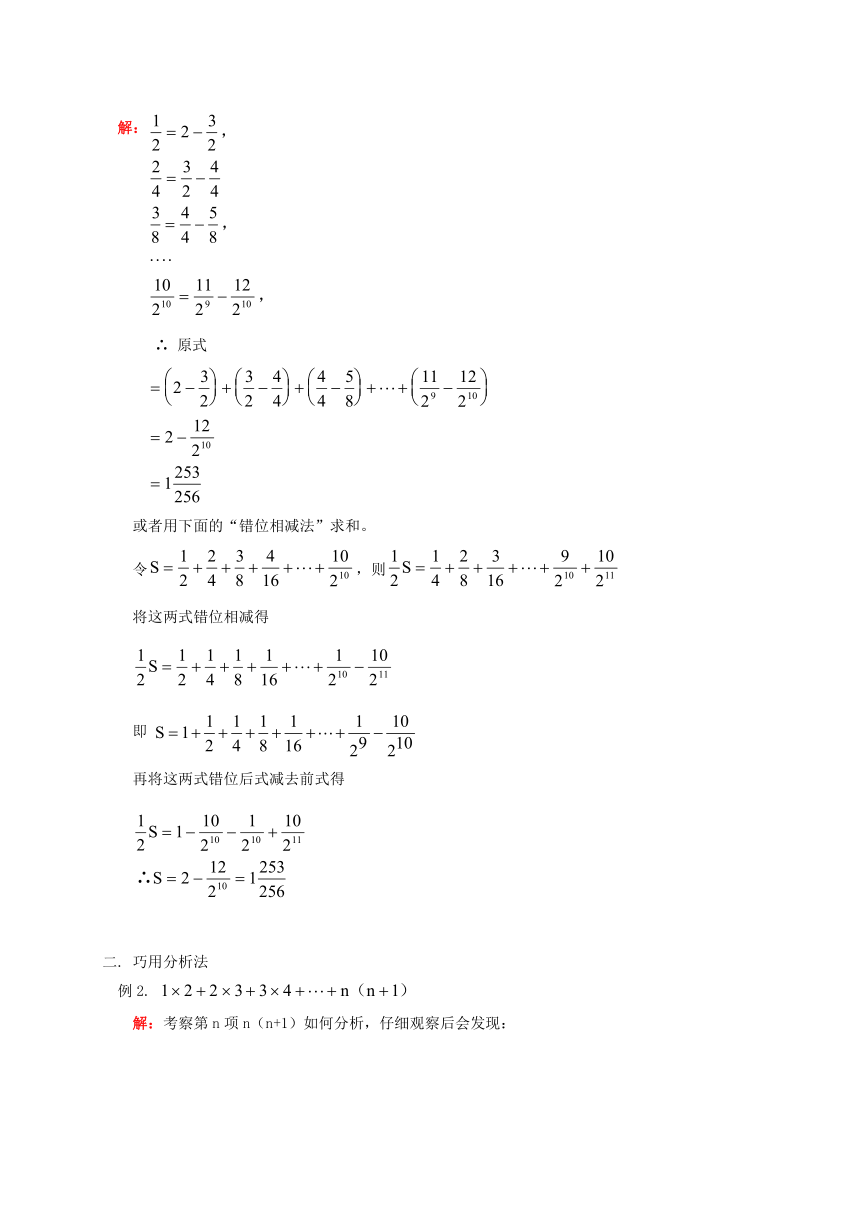

文档简介
有理数的混合运算——简便运算技巧(2)
【本讲教育信息】
一.
教学内容:
有理数的混合运算——简便运算技巧(2)
二.
重点、难点:
有理数运算是中学数学中一切运算的基础,准确地理解有理数相关的概念,以及它的运算法则、公式,并且善于根据所给题目要求,将推理与计算相结合,灵活巧妙地选择简捷的算法,可以很好地提高思维的敏捷性。将现实中的问题与学习中的知识相结合,并合理的解决它,你会发现数学的很多乐趣。
三.
我们的目标:
当我们认识了零、负整数和负分数后,就引出了有理数的概念。整数(正整数、零、负整数)和分数(正分数、负分数)统称有理数,任何一个有理数都可以表示为一个既约分数均为整数且互素)。并且,有理数可以比较大小,有理数的和、差、积、商(分母不为零)仍为有理数,任意两个有理数之间都有无穷个有理数,有理数运算是中学数学中一切运算的基础,它要求同学们在理解有理数的有关概念、法则的基础上,能根据法则,公式等正确、迅速地进行运算,同时还要善于根据题目条件,将推理与计算相结合,灵活巧妙地选择合理的简捷的算法解决问题,从而提高运算能力,发展思维的敏捷性与灵活性。
【典型例题】
一.
巧用错位相减
例1.
;
解:
∴
原式
或者用下面的“错位相减法”求和。
令,则
将这两式错位相减得
即
再将这两式错位后式减去前式得
二.
巧用分析法
例2.
解:考察第n项n(n+1)如何分析,仔细观察后会发现:
∴
原式
说明:分析和错位相减是有理数运算中常用的技巧,在解题中应注意总结归纳规律,力求灵活应用。
三.
巧换元
例3.
计算:
解:设,则
原式
例4.
;
解:直接计算较繁,仔细观察分母中涉及到三个连续整数:12345,12346,12347,可设字母n=12346,那么12345=n-1,12347=n+1,于是分母变为,即原式分母的值是1。
∴原式=24690。
四.
巧相约
例5.
计算:
解:原式
五.
巧用倒序配对
例6.
计算:
解:设原式,对括号内各项倒序排列后,再设
,则:
所以
所以原式
六.
巧用倒数法
例7.
计算
分析:因为与互为倒数,而比较容易计算,故此题只需先计算出后部分的结果即可。
解:因为
∴
原式
【模拟试题】(答题时间:30分钟)
1.
计算:
2.
计算:
3.
计算:
4.
计算:
【试题答案】
1.
解:设(1)
则(2)
则得:
即
(含整体思想)
2.
解:令
则原式
3.
解:令19991998=a,则
原式=
4.
解:设,把等式右边倒序排列,得
将两式相加,得
即,
∴
原式=4005
【本讲教育信息】
一.
教学内容:
有理数的混合运算——简便运算技巧(2)
二.
重点、难点:
有理数运算是中学数学中一切运算的基础,准确地理解有理数相关的概念,以及它的运算法则、公式,并且善于根据所给题目要求,将推理与计算相结合,灵活巧妙地选择简捷的算法,可以很好地提高思维的敏捷性。将现实中的问题与学习中的知识相结合,并合理的解决它,你会发现数学的很多乐趣。
三.
我们的目标:
当我们认识了零、负整数和负分数后,就引出了有理数的概念。整数(正整数、零、负整数)和分数(正分数、负分数)统称有理数,任何一个有理数都可以表示为一个既约分数均为整数且互素)。并且,有理数可以比较大小,有理数的和、差、积、商(分母不为零)仍为有理数,任意两个有理数之间都有无穷个有理数,有理数运算是中学数学中一切运算的基础,它要求同学们在理解有理数的有关概念、法则的基础上,能根据法则,公式等正确、迅速地进行运算,同时还要善于根据题目条件,将推理与计算相结合,灵活巧妙地选择合理的简捷的算法解决问题,从而提高运算能力,发展思维的敏捷性与灵活性。
【典型例题】
一.
巧用错位相减
例1.
;
解:
∴
原式
或者用下面的“错位相减法”求和。
令,则
将这两式错位相减得
即
再将这两式错位后式减去前式得
二.
巧用分析法
例2.
解:考察第n项n(n+1)如何分析,仔细观察后会发现:
∴
原式
说明:分析和错位相减是有理数运算中常用的技巧,在解题中应注意总结归纳规律,力求灵活应用。
三.
巧换元
例3.
计算:
解:设,则
原式
例4.
;
解:直接计算较繁,仔细观察分母中涉及到三个连续整数:12345,12346,12347,可设字母n=12346,那么12345=n-1,12347=n+1,于是分母变为,即原式分母的值是1。
∴原式=24690。
四.
巧相约
例5.
计算:
解:原式
五.
巧用倒序配对
例6.
计算:
解:设原式,对括号内各项倒序排列后,再设
,则:
所以
所以原式
六.
巧用倒数法
例7.
计算
分析:因为与互为倒数,而比较容易计算,故此题只需先计算出后部分的结果即可。
解:因为
∴
原式
【模拟试题】(答题时间:30分钟)
1.
计算:
2.
计算:
3.
计算:
4.
计算:
【试题答案】
1.
解:设(1)
则(2)
则得:
即
(含整体思想)
2.
解:令
则原式
3.
解:令19991998=a,则
原式=
4.
解:设,把等式右边倒序排列,得
将两式相加,得
即,
∴
原式=4005
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
