辽宁省凌海市七年级数学下册课后补习班辅导直线平行的条件与性质讲学案(附答案)
文档属性
| 名称 | 辽宁省凌海市七年级数学下册课后补习班辅导直线平行的条件与性质讲学案(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 240.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 00:00:00 | ||
图片预览




文档简介
直线平行的条件与性质
【本讲教育信息】
一.
教学内容:
直线平行的条件与性质
[目标]
1.
掌握直线平行的条件以及同位角、内错角、同旁内角的特征。
2.
理解直线平行的性质,能初步运用直线平行的性质进行有关计算。
二.
重、难点:
1.
直线平行的条件与性质及同位角、内错角、同旁内角的特征。
2.
正确区分平行线的性质和判定。
三.
知识要点
1.
相关概念:
(1)在同一平面内,不相交的两条直线叫做平行线。
平行线的定义包含三层意思:
①“在同一平面内”是前提条件;
②“不相交”是指两条直线没有交点;
③平行线指的是”两条直线”,而不是两条射线或两条线段
(2)
2.
直线平行的条件(判定)
两条直线被第三条直线所截
(1)若同位角相等,则两直线平行;
(2)若内错角相等,则两直线平行;
(3)若同旁内角互补,则两直线平行
3.
平行线的性质
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。
简单地说,就是:
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补。
4.
直线平行的条件与性质的区别
由角的已知条件推出两线的平行的结论是平行线的判定;
而由两线的平行的条件推出角的结论则是平行线的性质。
【典型例题】
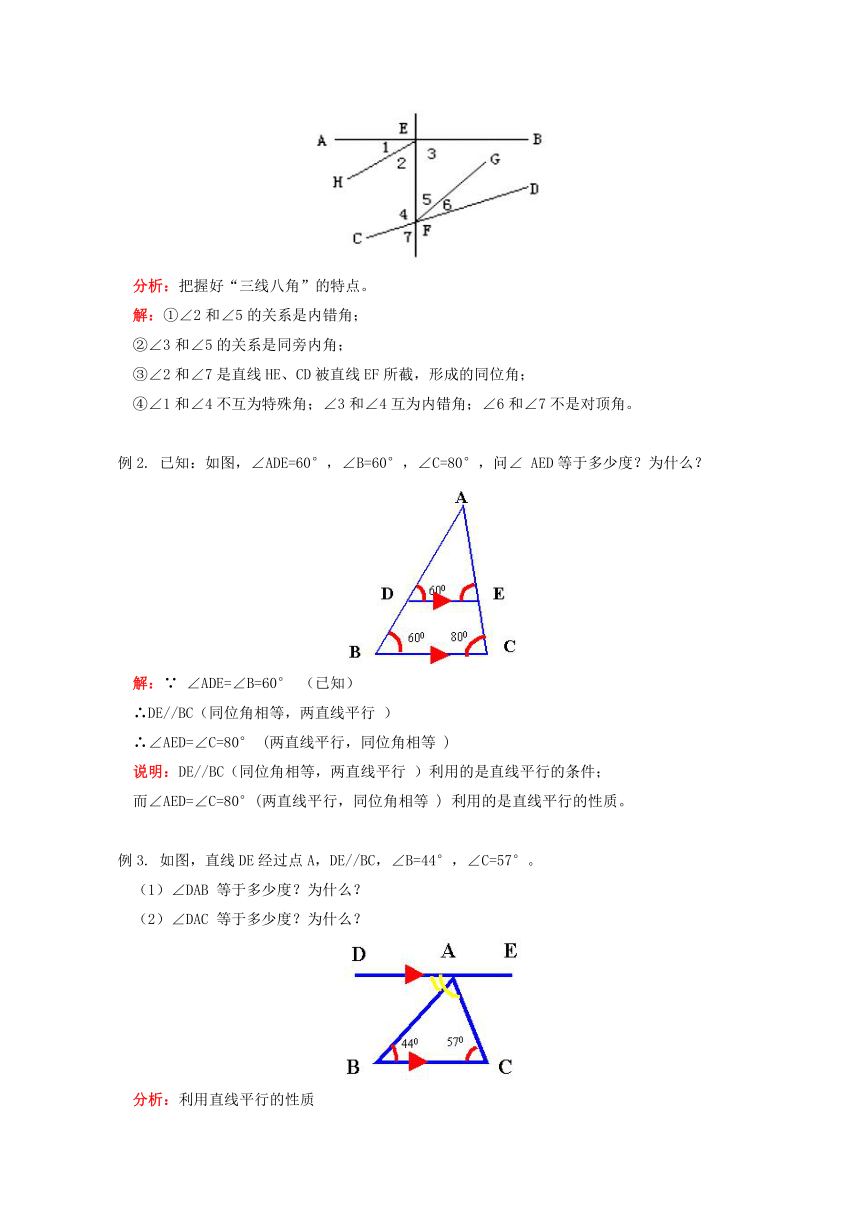
例1.
指出图中,①∠2和∠5的关系是______;②∠3和∠5的关系是______;③∠2和∠
__是直线______、______被直线______所截,形成的同位角;④∠1和∠4呢?∠3和∠4呢?∠6和∠7是对顶角吗?
分析:把握好“三线八角”的特点。
解:①∠2和∠5的关系是内错角;
②∠3和∠5的关系是同旁内角;
③∠2和∠7是直线HE、CD被直线EF所截,形成的同位角;
④∠1和∠4不互为特殊角;∠3和∠4互为内错角;∠6和∠7不是对顶角。
例2.
已知:如图,∠ADE=60°,∠B=60°,∠C=80°,问∠
AED等于多少度?为什么?
解:∵
∠ADE=∠B=60°
(已知)
∴DE//BC(同位角相等,两直线平行
)
∴∠AED=∠C=80°
(两直线平行,同位角相等
)
说明:DE//BC(同位角相等,两直线平行
)利用的是直线平行的条件;
而∠AED=∠C=80°(两直线平行,同位角相等
)
利用的是直线平行的性质。
例3.
如图,直线DE经过点A,DE//BC,∠B=44°,∠C=57°。
(1)∠DAB
等于多少度?为什么?
(2)∠DAC
等于多少度?为什么?
分析:利用直线平行的性质
解:(1)∠DAB
=44°(两直线平行,内错角相等)
(2)∠DAC=180°-57°=123°(两直线平行,同旁内角互补)
例4.
如图,∠BAC与∠ACD的平分线交于点E,且∠1+∠2=90°.AB与CD平行吗 为什么
分析:结合角平分线的性质构造同旁内角的和。
解:AB与CD平行
∵AE、CE分别是∠BAC与∠ACD的平分线
∴∠BAC=2∠1,∠ACD=2∠2
∴∠BAC+ACD=2(∠1+∠2)=180°
∴AB∥CD(同旁内角互补,两直线平行)
例5.
如图,A、B、C、D四点在同一条直线上,EA⊥AD,FB⊥AD,垂足分别为A、B,∠E=∠F。CE与DF是否平行 为什么
分析:平面内,垂直于同一直线的两直线平行
解:∵EA⊥AD,FB⊥AD
∴EA∥FB
∴∠E=∠BGC(两直线平行,同位角相等)
又∵∠E=∠F
∴∠BGC
=∠F
∴CE∥DF(同位角相等,两直线平行)
例6.
如图,∠1=∠B,∠2=∠3,
∠4=85°,试求∠ADC的度数。
解:∵∠1=∠B
∴DG∥BC(同位角相等,两直线平行)
∴∠2=∠DCB(两直线平行,内错角相等)
∵∠2=∠3
∴∠3=∠DCB
∴DC∥EF(同位角相等,两直线平行)
∴∠ADC=∠4=85°(两直线平行,同位角相等)
说明:本题多次运用了两直线平行的条件与性质,要牢牢把握好它们之间的转化关系。
例7.
如图、点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断BE与AC的位置关系吗?请说明理由。
解:∵BE平分∠ABD,
∴∠DBE=∠ABE(角平分线性质)
∵∠DBE=∠A
∴∠A=∠ABE
∴BE∥AC(内错角相等,两直线平行)
说明:角平分线的性质在此类题目中经常出现,如何恰当的运用角平分线的性质是解题的关键。
例8.
如图,是一块小木板,在它上面画了一条线段AB,如果要求用量角器,通过度量某些角的大小来判断木板的上下边缘是否平行,你准备怎样去做?
分析:此题为一个实际应用题,如若转化为我们常见的数学问题则非常简单。要验证木板的上下边缘是否平行,我们通过第三条与之均相交的直线AB来考查。所以,只要使用量角器量一下内错角或同旁内角即可。
解略。
说明:内错角相等,两直线平行;同旁内角互补,两直线平行。
例9.
如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
分析:补形后转化成一般的数学模型解决问题。
解:∵梯形的上下底平行
即AD∥BC
∴∠A+
∠B=
180°
∠D+∠C=
180°(两直线平行,同旁内角互补).
又∵∠A=115°;∠D=100°.
(已知)
∴∠B=
180°-115°=65°
∠C=180°-100°=
80°
答:梯形的另外两个角分别是65°、
80°.
例10.
如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行。第一次拐的角∠B等于142°,第二次拐的角∠C是多少度?为什么?
答:∠C=142°
因为拐弯前后的两条路互相平行,∠B和∠C是两条平行线的内错角,根据两直线平行,内错角相等,∠C=∠B=142°
【模拟试题】(答题时间:40分钟)
1.
下图中,∠1和∠2是同位角的是(
)
2.
如图,直线l1、l2被l所截,下列说理过程正确的是(
).
A.
因为∠1与∠2互补,所以l1∥l2
B.
如果∠2=∠3,那么l1∥l2
C.
如果∠1=∠2,那么l1∥l2
D.
如果∠1=∠3,那么l1∥l2
3.
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是(
)
A.
第一次向右拐40°,第二次向左拐140°
B.
第一次向左拐40°,第二次向右拐40°
C.
第一次向左拐40°,第二次向右拐140°
D.
第一次向右拐40°,第二次向右拐40°
4.
如图所示,∥,AB⊥,∠ABC=130°,那么∠α的度数为( )
A.
60°
B.
50°
C.
40°
D.
30°
5.
已知如图,∠1=∠B,则
∥
,若∠3=∠4,则
∥
;
6.已知如图,a∥b,且∠1=117°,则∠3=
°;
7.
如图,已知AB∥DE,∠ABC=80°,∠CDE=140°,则∠BCD=
.
8.
如图所示,OP∥QR∥ST,若∠2=110°,∠3=120°,则∠1=
。
9.
如图所示,已知∠AOB=50°,PC∥OB,PD平分∠OPC,则∠APC=
°,∠PDO=
°
10.
两条平行直线被第三条直线所截,则
①一对同位角的角平分线互相平行;
②一对内错角的角平分线互相平行;
③一对同旁内角的角平分线互相平行;
④一对同旁内角的角平分线互相垂直.
其中正确的结论是
.
(注:请把你认为所有正确的结论的序号都填上)
11.
(1)以D为顶点,DA为边作一个角,使它等于∠ABC,作出的角的另一边与BC平行吗?
答:
(2)如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,你能找到几对平行线?说说你的理由.
答:
12.
(1)图中,若∠AMC=38°,则∠BNF等于多少度时,有CD∥EF?说说你的理由。
答:
(2)学着说点理:如图:∠1=∠2=∠3,完成说理过程并注明理由:
因为
∠1=∠2
所以
____∥____
(
)
因为
∠1=∠3
所以
____∥____
(
)
13.
如图,已知∠AEC=∠A+∠C,试说明:AB∥CD。
14.
如图所示,AB∥DF,DE∥BC,∠1=65°,求∠2,∠3的度数,并说明理由。
15.
如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?
【试题答案】
1.
D
2.
D
3.
B
4.
C
5.
AD、BC,AB、CD
6.
63°
7.
40°
8.
50°
9.
50°,65°
10.
①②④
11.
解:(1)不一定平行。如图所示
(2)①IG∥EF。因为∠IGA=127°,所以∠IGB=53°
又因为∠EFB=53°,所以IG∥EF;
②AB∥CD。因为∠IGA=127°,所以∠BGH=127°
所以∠BGH+∠GHD=180°。所以AB∥CD
12.
解:(1)∠BNF=38°。理由略
(2)EF,BD,同位角相等,两直线平行
AB,CD,内错角相等,两直线平行
13.
解:过点E作EF∥AB
又
而∠AEC=∠AEF+∠CEF
∴∠CEF=∠C
∴EF∥CD
∴AB∥CD
14.
解:∥
又
∥
15.
证:由OE⊥OA,得∠2+∠3=90°,又∠1=∠2,∠1+∠2+∠3+∠4=180°
∴∠3=∠4,而∠5=90°-∠3,∠6=90°-∠4,∴得证。
【本讲教育信息】
一.
教学内容:
直线平行的条件与性质
[目标]
1.
掌握直线平行的条件以及同位角、内错角、同旁内角的特征。
2.
理解直线平行的性质,能初步运用直线平行的性质进行有关计算。
二.
重、难点:
1.
直线平行的条件与性质及同位角、内错角、同旁内角的特征。
2.
正确区分平行线的性质和判定。
三.
知识要点
1.
相关概念:
(1)在同一平面内,不相交的两条直线叫做平行线。
平行线的定义包含三层意思:
①“在同一平面内”是前提条件;
②“不相交”是指两条直线没有交点;
③平行线指的是”两条直线”,而不是两条射线或两条线段
(2)
2.
直线平行的条件(判定)
两条直线被第三条直线所截
(1)若同位角相等,则两直线平行;
(2)若内错角相等,则两直线平行;
(3)若同旁内角互补,则两直线平行
3.
平行线的性质
(1)两条平行线被第三条直线所截,同位角相等;
(2)两条平行线被第三条直线所截,内错角相等;
(3)两条平行线被第三条直线所截,同旁内角互补。
简单地说,就是:
(1)两直线平行,同位角相等;
(2)两直线平行,内错角相等;
(3)两直线平行,同旁内角互补。
4.
直线平行的条件与性质的区别
由角的已知条件推出两线的平行的结论是平行线的判定;
而由两线的平行的条件推出角的结论则是平行线的性质。
【典型例题】
例1.
指出图中,①∠2和∠5的关系是______;②∠3和∠5的关系是______;③∠2和∠
__是直线______、______被直线______所截,形成的同位角;④∠1和∠4呢?∠3和∠4呢?∠6和∠7是对顶角吗?
分析:把握好“三线八角”的特点。
解:①∠2和∠5的关系是内错角;
②∠3和∠5的关系是同旁内角;
③∠2和∠7是直线HE、CD被直线EF所截,形成的同位角;
④∠1和∠4不互为特殊角;∠3和∠4互为内错角;∠6和∠7不是对顶角。
例2.
已知:如图,∠ADE=60°,∠B=60°,∠C=80°,问∠
AED等于多少度?为什么?
解:∵
∠ADE=∠B=60°
(已知)
∴DE//BC(同位角相等,两直线平行
)
∴∠AED=∠C=80°
(两直线平行,同位角相等
)
说明:DE//BC(同位角相等,两直线平行
)利用的是直线平行的条件;
而∠AED=∠C=80°(两直线平行,同位角相等
)
利用的是直线平行的性质。
例3.
如图,直线DE经过点A,DE//BC,∠B=44°,∠C=57°。
(1)∠DAB
等于多少度?为什么?
(2)∠DAC
等于多少度?为什么?
分析:利用直线平行的性质
解:(1)∠DAB
=44°(两直线平行,内错角相等)
(2)∠DAC=180°-57°=123°(两直线平行,同旁内角互补)
例4.
如图,∠BAC与∠ACD的平分线交于点E,且∠1+∠2=90°.AB与CD平行吗 为什么
分析:结合角平分线的性质构造同旁内角的和。
解:AB与CD平行
∵AE、CE分别是∠BAC与∠ACD的平分线
∴∠BAC=2∠1,∠ACD=2∠2
∴∠BAC+ACD=2(∠1+∠2)=180°
∴AB∥CD(同旁内角互补,两直线平行)
例5.
如图,A、B、C、D四点在同一条直线上,EA⊥AD,FB⊥AD,垂足分别为A、B,∠E=∠F。CE与DF是否平行 为什么
分析:平面内,垂直于同一直线的两直线平行
解:∵EA⊥AD,FB⊥AD
∴EA∥FB
∴∠E=∠BGC(两直线平行,同位角相等)
又∵∠E=∠F
∴∠BGC
=∠F
∴CE∥DF(同位角相等,两直线平行)
例6.
如图,∠1=∠B,∠2=∠3,
∠4=85°,试求∠ADC的度数。
解:∵∠1=∠B
∴DG∥BC(同位角相等,两直线平行)
∴∠2=∠DCB(两直线平行,内错角相等)
∵∠2=∠3
∴∠3=∠DCB
∴DC∥EF(同位角相等,两直线平行)
∴∠ADC=∠4=85°(两直线平行,同位角相等)
说明:本题多次运用了两直线平行的条件与性质,要牢牢把握好它们之间的转化关系。
例7.
如图、点B在DC上,BE平分∠ABD,∠DBE=∠A,你能判断BE与AC的位置关系吗?请说明理由。
解:∵BE平分∠ABD,
∴∠DBE=∠ABE(角平分线性质)
∵∠DBE=∠A
∴∠A=∠ABE
∴BE∥AC(内错角相等,两直线平行)
说明:角平分线的性质在此类题目中经常出现,如何恰当的运用角平分线的性质是解题的关键。
例8.
如图,是一块小木板,在它上面画了一条线段AB,如果要求用量角器,通过度量某些角的大小来判断木板的上下边缘是否平行,你准备怎样去做?
分析:此题为一个实际应用题,如若转化为我们常见的数学问题则非常简单。要验证木板的上下边缘是否平行,我们通过第三条与之均相交的直线AB来考查。所以,只要使用量角器量一下内错角或同旁内角即可。
解略。
说明:内错角相等,两直线平行;同旁内角互补,两直线平行。
例9.
如图是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=100°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
分析:补形后转化成一般的数学模型解决问题。
解:∵梯形的上下底平行
即AD∥BC
∴∠A+
∠B=
180°
∠D+∠C=
180°(两直线平行,同旁内角互补).
又∵∠A=115°;∠D=100°.
(已知)
∴∠B=
180°-115°=65°
∠C=180°-100°=
80°
答:梯形的另外两个角分别是65°、
80°.
例10.
如图,一条公路两次拐弯后,和原来的方向相同,也就是拐弯前后的两条路互相平行。第一次拐的角∠B等于142°,第二次拐的角∠C是多少度?为什么?
答:∠C=142°
因为拐弯前后的两条路互相平行,∠B和∠C是两条平行线的内错角,根据两直线平行,内错角相等,∠C=∠B=142°
【模拟试题】(答题时间:40分钟)
1.
下图中,∠1和∠2是同位角的是(
)
2.
如图,直线l1、l2被l所截,下列说理过程正确的是(
).
A.
因为∠1与∠2互补,所以l1∥l2
B.
如果∠2=∠3,那么l1∥l2
C.
如果∠1=∠2,那么l1∥l2
D.
如果∠1=∠3,那么l1∥l2
3.
一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是(
)
A.
第一次向右拐40°,第二次向左拐140°
B.
第一次向左拐40°,第二次向右拐40°
C.
第一次向左拐40°,第二次向右拐140°
D.
第一次向右拐40°,第二次向右拐40°
4.
如图所示,∥,AB⊥,∠ABC=130°,那么∠α的度数为( )
A.
60°
B.
50°
C.
40°
D.
30°
5.
已知如图,∠1=∠B,则
∥
,若∠3=∠4,则
∥
;
6.已知如图,a∥b,且∠1=117°,则∠3=
°;
7.
如图,已知AB∥DE,∠ABC=80°,∠CDE=140°,则∠BCD=
.
8.
如图所示,OP∥QR∥ST,若∠2=110°,∠3=120°,则∠1=
。
9.
如图所示,已知∠AOB=50°,PC∥OB,PD平分∠OPC,则∠APC=
°,∠PDO=
°
10.
两条平行直线被第三条直线所截,则
①一对同位角的角平分线互相平行;
②一对内错角的角平分线互相平行;
③一对同旁内角的角平分线互相平行;
④一对同旁内角的角平分线互相垂直.
其中正确的结论是
.
(注:请把你认为所有正确的结论的序号都填上)
11.
(1)以D为顶点,DA为边作一个角,使它等于∠ABC,作出的角的另一边与BC平行吗?
答:
(2)如图,∠EFB=∠GHD=53°,∠IGA=127°,由这些条件,你能找到几对平行线?说说你的理由.
答:
12.
(1)图中,若∠AMC=38°,则∠BNF等于多少度时,有CD∥EF?说说你的理由。
答:
(2)学着说点理:如图:∠1=∠2=∠3,完成说理过程并注明理由:
因为
∠1=∠2
所以
____∥____
(
)
因为
∠1=∠3
所以
____∥____
(
)
13.
如图,已知∠AEC=∠A+∠C,试说明:AB∥CD。
14.
如图所示,AB∥DF,DE∥BC,∠1=65°,求∠2,∠3的度数,并说明理由。
15.
如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?
【试题答案】
1.
D
2.
D
3.
B
4.
C
5.
AD、BC,AB、CD
6.
63°
7.
40°
8.
50°
9.
50°,65°
10.
①②④
11.
解:(1)不一定平行。如图所示
(2)①IG∥EF。因为∠IGA=127°,所以∠IGB=53°
又因为∠EFB=53°,所以IG∥EF;
②AB∥CD。因为∠IGA=127°,所以∠BGH=127°
所以∠BGH+∠GHD=180°。所以AB∥CD
12.
解:(1)∠BNF=38°。理由略
(2)EF,BD,同位角相等,两直线平行
AB,CD,内错角相等,两直线平行
13.
解:过点E作EF∥AB
又
而∠AEC=∠AEF+∠CEF
∴∠CEF=∠C
∴EF∥CD
∴AB∥CD
14.
解:∥
又
∥
15.
证:由OE⊥OA,得∠2+∠3=90°,又∠1=∠2,∠1+∠2+∠3+∠4=180°
∴∠3=∠4,而∠5=90°-∠3,∠6=90°-∠4,∴得证。
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
