2016-2017学年高一数学人教B版必修1学案(学习导航 ):2.1.3函数的单调性
文档属性
| 名称 | 2016-2017学年高一数学人教B版必修1学案(学习导航 ):2.1.3函数的单调性 |
|
|
| 格式 | zip | ||
| 文件大小 | 190.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 00:00:00 | ||
图片预览



文档简介
2.1.3
函数的单调性
自主整理
函数的单调性
(1)一般地,设函数y=f(x)的定义域为A,区间MA.
如果取区间M内的任意两个值x1,x2,则
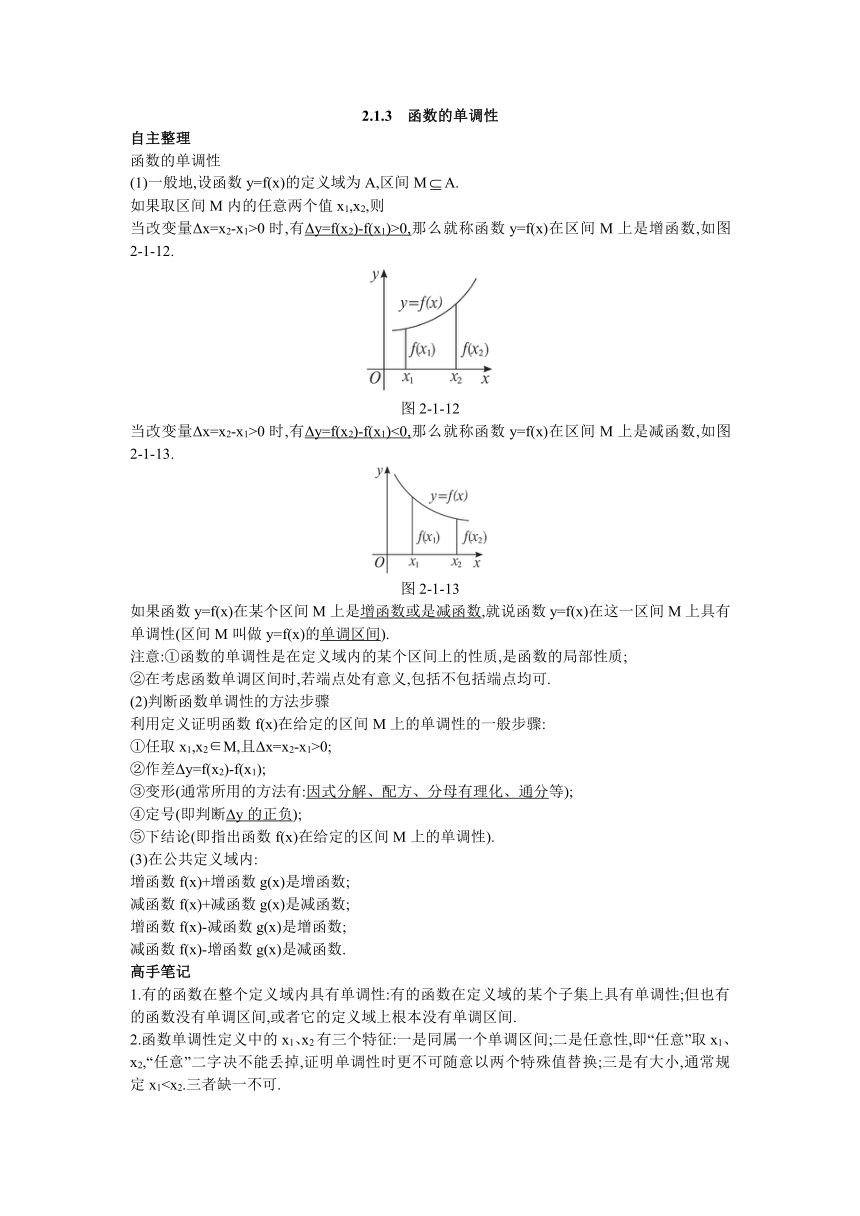
当改变量Δx=x2-x1>0时,有Δy=f(x2)-f(x1)>0,那么就称函数y=f(x)在区间M上是增函数,如图2-1-12.
图2-1-12
当改变量Δx=x2-x1>0时,有Δy=f(x2)-f(x1)<0,那么就称函数y=f(x)在区间M上是减函数,如图2-1-13.
图2-1-13
如果函数y=f(x)在某个区间M上是增函数或是减函数,就说函数y=f(x)在这一区间M上具有单调性(区间M叫做y=f(x)的单调区间).
注意:①函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
②在考虑函数单调区间时,若端点处有意义,包括不包括端点均可.
(2)判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间M上的单调性的一般步骤:
①任取x1,x2∈M,且Δx=x2-x1>0;
②作差Δy=f(x2)-f(x1);
③变形(通常所用的方法有:因式分解、配方、分母有理化、通分等);
④定号(即判断Δy的正负);
⑤下结论(即指出函数f(x)在给定的区间M上的单调性).
(3)在公共定义域内:
增函数f(x)+增函数g(x)是增函数;
减函数f(x)+减函数g(x)是减函数;
增函数f(x)-减函数g(x)是增函数;
减函数f(x)-增函数g(x)是减函数.
高手笔记
1.有的函数在整个定义域内具有单调性:有的函数在定义域的某个子集上具有单调性;但也有的函数没有单调区间,或者它的定义域上根本没有单调区间.
2.函数单调性定义中的x1、x2有三个特征:一是同属一个单调区间;二是任意性,即“任意”取x1、x2,“任意”二字决不能丢掉,证明单调性时更不可随意以两个特殊值替换;三是有大小,通常规定x13.利用函数的单调性的定义比较大小,一方面是正向应用,即若f(x)在给定的区间上是增函数,当x1x2时,f(x1)>f(x2);另一方面是逆向应用,即若f(x)在给定的区间上是增函数,当f(x1)f(x2)时x1>x2.当f(x)是减函数时类同.
4.利用函数单调性判断函数的最大(小)值:如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b).
5.记忆口诀:
增函数,减函数,函数作差要记住;
正号增,负号减,增减函数很简单;
往上增,往下减,增减趋势正相反.
名师解惑
1.对于函数单调性的理解应注意什么
剖析:对于函数单调性的理解,要注意以下几点:
(1)函数的单调性只能在函数的定义域内来讨论,可以是整个定义域,也可以是定义域的某个区间.
(2)函数f(x)在给定区间上的单调性,反映了函数f(x)在这个区间上函数值的总体变化趋势,是函数在这个区间上的整体性质.
(3)函数的单调性是对于某个区间而言的,所以要受到区间的限制.如果函数在某个区间上是单调的,那么在这个区间的子集上也是单调的;但是如果函数在某几个区间上具有相同的单调性,在这几个区间的并集上则不一定具有单调性.2.判断或证明函数在某区间上的单调性一定要用定义吗?函数单调性的判定方法主要有哪些呢
剖析:(1)一般来说,证明或判断函数的单调性,严格地说必须用增、减函数定义,其步骤是:设出指定区间上的任意两个值→作差→变形→判符号→定结论.但对于求解选择、填空之类的不要求解过程的问题,能结合图象快速指出单调区间,当然也是可行的.但根据函数图象判断函数单调性,必须按照作函数图象的步骤准确画出函数图象,特别要弄清楚由上升到下降和由下降到上升的关键点的横坐标,才能写出其单调区间,如果一个函数有两个单调递增区间,应写成(-∞,-1),[1,+∞)或(-∞,-1)和[1,+∞)等形式,但不能写成(-∞,-1)∪[1,+∞)的形式.
(2)判断函数单调性的方法是本节的重点,常用的方法有:
①定义法:利用定义严格判断.
②图象法:根据函数图象直观判断.
③直接法:运用已知的结论,直接得到函数的单调性.如一次函数、二次函数、反比例函数的单调性均可直接说出.多了解几点结论,对于直接判断函数的单调性更有好处,如:
函数y=-f(x)与函数y=f(x)的单调性相反;当y=f(x)恒为负时,函数y=与y=f(x)的单调性相反;
在公共区间内,增函数+增函数=增函数,增函数-减函数=增函数等.
y=f(x)与y=kf(x)(k≠0),当k>0时,增减性相同,当k<0时,增减性相反.
3.如何求函数在某闭区间上的最值
剖析:如果函数y=f(x)在闭区间[a,b]上具有单调性,那么它在这个区间上必取得最大值和最小值.即当f(x)在[a,b]上递增时,ymax=f(b),ymin=f(a);当f(x)在[a,b]上递减时,ymax=f(a),ymin=f(b).
如果函数y=f(x)在给定的闭区间[a,b]上不具有单调性,那么也就没有上述确定的结论了,那就要具体问题具体分析了.
讲练互动
【例题1】求函数y=|x+1|+|x-2|的单调区间,以及在每一个区间上的单调性.分析:本题考查单调区间的判定,在解题时应用数形结合思想,通过图象寻找单调区间.
图2-1-14
解:将函数化为分段函数形式:
y=
画出它的图象(图2-1-14),由图象,可知单调递增区间为[2,+∞),单调递减区间为(-∞,-1].
绿色通道
(1)函数的单调性是对某个区间而言的,若在某区间,函数值为唯一确定常数时,我们称函数在该区间没有单调性.(对于单独的一点,因为没有增减变化,所以显然不存在单调性问题)(2)对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此在考虑它的单调区间时,包括不包括端点都可以;还要注意定义域内不包含的点,不应出现在单调区间里.
(3)分段函数是历年高考的热门话题,常考常新,值得我们在平时认真对待.
变式训练1.已知函数f(x)=x2-5x+6.
(1)求其单调区间;
(2)用定义法证明其单调性.
分析:(1)运用函数图象找单调区间是求解函数单调性的基本方法.对于二次函数,其图象为抛物线.单调区间的界定与对称轴有关;而单调增减性与开口有关.所以考查二次函数问题,一定得两看(看二次项系数,看对称轴).
(2)定义作差法是证明函数单调性的一般方法,而有时通过定义作差法也可以直接找出单调区间.
解:(1)f(x)=(x)2,它是以(,)为顶点,对称轴平行于y轴、开口向上的抛物线,如图所示,可得单调区间是(-∞,]与(,+∞).
其中在(-∞,]上是减函数,在(,+∞)上是增函数.
(2)定义法证明如下:
任取x1、x2,设x1f(x1)-f(x2)=x12-x22-5(x1-x2)
=(x1+x2-5)(x1-x2).
∵x1∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴f(x)=x2-5x+6在(-∞,]上是减函数.
类似地,可以证明f(x)在(,+∞)上是增函数.
【例题2】讨论函数f(x)=x+(a>0)的单调性.
分析:可以先讨论函数在(0,+∞)上的单调性,然后可类似地讨论在(-∞,)、[,0)、(0,]上的单调性.
解:∵x≠0,∴下面先讨论f(x)=x+在(0,+∞)上的单调性.
设0∵当01,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
故f(x)在(0,]上是减函数.
∵当a≤x1∴f(x1)-f(x2)<0,即f(x1)故f(x)在[,+∞)上是增函数.
同理我们可得f(x)在(-∞,]上是增函数;f(x)在[,0)上是减函数.
黑色陷阱
判断单调性时,我们可以用口诀“同向则增,异向则减”帮助理解.在证明时,化简是必不可少的,不能想当然地认为谁大谁小而直接下结论,一般情况下,我们应该化简到出现因式相乘,或者出现完全平方式为止,然后通过已知条件对符号进行判断.含参数函数单调性的判定,往往对参数要分类讨论.本题的结论十分重要,在一些问题的求解中十分有用,应予重视.
变式训练
2.讨论函数y=(-1分析:此题给出了函数解析式,按照定义去判断单调性即可.由于含有参数a,故要对a进行分类讨论.
解:设-1∵-10,x1x2+1>0,x12-1<0,x22-1<0.
∴当a<0时,f(x1)当a>0时,f(x1)>f(x2),f(x)在(-1,1)上是减函数.
当a=0时,f(x)为常数函数,没有单调性.
【例题3】判断函数f(x)=的单调性.
分析:可把函数的分子拼凑成分母的形式,转化成只在分母中含有变量x的形式,写出它的单调区间.解:原函数可化为f(x)=+1,该函数的定义域为{x|x≠1}.显然f(x)的图象是由y=的图象先向右平移1个单位,再向上平移1个单位而得到的.
由于y=在(-∞,0)上是减函数,在(0,+∞)上也是减函数,
从而f(x)=在(-∞,1)上是减函数,在(1,+∞)上也是减函数.
所以函数f(x)=在(-∞,1)和(1,+∞)上都是减函数.
绿色通道
把未知的问题转化为已知的问题,用已知问题的解还原说明未知问题的解,这是学好数学的一种常用方法.解决这种分式函数问题,需掌握“凑分母”化简的方法.变式训练
3.函数y=在(-2,+∞)上单调递增,则实数a的取值范围为.
解析:y===a.
因原式在(-2,+∞)上单调递增,
设-2则.
∴.
∵0∴a-1>0,即a>1.
故实数a的取值范围是(1,+∞).
答案:(1,+∞)
【例题4】已知≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a).
(1)求g(a)的函数表达式;
(2)判断函数g(a)在区间[,1]上的单调性,并求出g(a)的最小值.
分析:(1)属于“轴变区间定”问题,需要对对称轴与区间的关系进行讨论.(2)由于g(a)是分段函数,其单调性的判断方法是分别将各个区间上的解析式单独判断,然后再结合各区间的单调性求最小值.
解:(1)∵≤a≤1,∴f(x)的图象为开口向上的抛物线,且对称轴为x=∈[1,3].
∴f(x)有最小值N(a)=f()=1.
当2≤≤3时,a∈[,],f(x)有最大值M(a)=f(1)=a-1;
当1≤<2时,a∈(,1],f(x)有最大值M(a)=f(3)=9a-5.
∴g(a)=
9a-6+,(2)设≤a10,∴g(a1)>g(a2).
∴g(a)在[,]上是减函数.
设∴g(a)在(,1]上是增函数.
∴当a=时,g(a)有最小值.
绿色通道
求分段函数的单调性时,需对构成分段函数的各解析式分别进行判断.如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减,则函数y=f(x)在区间[a,c]上有最大值f(b);如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增,则函数y=f(x)在区间[a,c]上有最小值f(b).
变式训练
4.已知点P(t,y)在函数f(x)=(x≠-1)的图象上,且有t2-c2at+4c2=0(c≠0).
(1)求证:|ac|≥4;
(2)求证:在(-1,+∞)上f(x)单调递增;
(3)求证:f(|a|)+f(|c|)>1.
分析:在解决函数定义域、值域、比较两数大小、不等式的证明等具体问题中均可能用到函数的单调性,要充分运用,灵活处理.而一元二次方程的问题,有时往往可以根据需要去判定Δ的符号,从而得到不等式.本题还需运用分离常数法化简分式,要懂得借鉴.
解:(1)∵t∈R,t≠-1,∴Δ=(-c2a)2-16c2=c4a2-16c2=c2(c2a2-16)≥0.
∵c≠0,∴c2>0.∴c2a2≥16.∴|ac|≥4.
(2)由f(x)=,
设-1∵-10,x1+1>0,x2+1>0.
∴f(x2)-f(x1)>0,即f(x2)>f(x1).
∴x>-1时,f(x)单调递增.
(3)∵f(x)在x>-1时单调递增,|c|≥>0,
∴f(|c|)≥f()=.
∴f(|a|)+f(|c|)≥f(|a|)+f()==1,
即f(|a|)+f(|c|)>1.
教材链接
[探索与研究]
函数值的改变量与自变量改变量的比叫做函数y=f(x)从x1到x2之间的平均变化率.
研究一个函数在某区间上是增函数还是减函数时,你能否根据函数的平均变化率,即比值的符号来判断函数y=f(x)在某区间上是增函数还是减函数 比值的大小与函数值增长的快慢有什么关系
答:当函数的平均变化率为正数时,可判断函数y=f(x)是增函数;当函数的平均变化率为负数时,可判断函数y=f(x)是减函数.比值的大小与函数值增长的快慢有关系:当越大时,函数值增长越快,当越小时,函数值减少就越快.
函数的单调性
自主整理
函数的单调性
(1)一般地,设函数y=f(x)的定义域为A,区间MA.
如果取区间M内的任意两个值x1,x2,则
当改变量Δx=x2-x1>0时,有Δy=f(x2)-f(x1)>0,那么就称函数y=f(x)在区间M上是增函数,如图2-1-12.
图2-1-12
当改变量Δx=x2-x1>0时,有Δy=f(x2)-f(x1)<0,那么就称函数y=f(x)在区间M上是减函数,如图2-1-13.
图2-1-13
如果函数y=f(x)在某个区间M上是增函数或是减函数,就说函数y=f(x)在这一区间M上具有单调性(区间M叫做y=f(x)的单调区间).
注意:①函数的单调性是在定义域内的某个区间上的性质,是函数的局部性质;
②在考虑函数单调区间时,若端点处有意义,包括不包括端点均可.
(2)判断函数单调性的方法步骤
利用定义证明函数f(x)在给定的区间M上的单调性的一般步骤:
①任取x1,x2∈M,且Δx=x2-x1>0;
②作差Δy=f(x2)-f(x1);
③变形(通常所用的方法有:因式分解、配方、分母有理化、通分等);
④定号(即判断Δy的正负);
⑤下结论(即指出函数f(x)在给定的区间M上的单调性).
(3)在公共定义域内:
增函数f(x)+增函数g(x)是增函数;
减函数f(x)+减函数g(x)是减函数;
增函数f(x)-减函数g(x)是增函数;
减函数f(x)-增函数g(x)是减函数.
高手笔记
1.有的函数在整个定义域内具有单调性:有的函数在定义域的某个子集上具有单调性;但也有的函数没有单调区间,或者它的定义域上根本没有单调区间.
2.函数单调性定义中的x1、x2有三个特征:一是同属一个单调区间;二是任意性,即“任意”取x1、x2,“任意”二字决不能丢掉,证明单调性时更不可随意以两个特殊值替换;三是有大小,通常规定x1
4.利用函数单调性判断函数的最大(小)值:如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增则函数y=f(x)在x=b处有最小值f(b).
5.记忆口诀:
增函数,减函数,函数作差要记住;
正号增,负号减,增减函数很简单;
往上增,往下减,增减趋势正相反.
名师解惑
1.对于函数单调性的理解应注意什么
剖析:对于函数单调性的理解,要注意以下几点:
(1)函数的单调性只能在函数的定义域内来讨论,可以是整个定义域,也可以是定义域的某个区间.
(2)函数f(x)在给定区间上的单调性,反映了函数f(x)在这个区间上函数值的总体变化趋势,是函数在这个区间上的整体性质.
(3)函数的单调性是对于某个区间而言的,所以要受到区间的限制.如果函数在某个区间上是单调的,那么在这个区间的子集上也是单调的;但是如果函数在某几个区间上具有相同的单调性,在这几个区间的并集上则不一定具有单调性.2.判断或证明函数在某区间上的单调性一定要用定义吗?函数单调性的判定方法主要有哪些呢
剖析:(1)一般来说,证明或判断函数的单调性,严格地说必须用增、减函数定义,其步骤是:设出指定区间上的任意两个值→作差→变形→判符号→定结论.但对于求解选择、填空之类的不要求解过程的问题,能结合图象快速指出单调区间,当然也是可行的.但根据函数图象判断函数单调性,必须按照作函数图象的步骤准确画出函数图象,特别要弄清楚由上升到下降和由下降到上升的关键点的横坐标,才能写出其单调区间,如果一个函数有两个单调递增区间,应写成(-∞,-1),[1,+∞)或(-∞,-1)和[1,+∞)等形式,但不能写成(-∞,-1)∪[1,+∞)的形式.
(2)判断函数单调性的方法是本节的重点,常用的方法有:
①定义法:利用定义严格判断.
②图象法:根据函数图象直观判断.
③直接法:运用已知的结论,直接得到函数的单调性.如一次函数、二次函数、反比例函数的单调性均可直接说出.多了解几点结论,对于直接判断函数的单调性更有好处,如:
函数y=-f(x)与函数y=f(x)的单调性相反;当y=f(x)恒为负时,函数y=与y=f(x)的单调性相反;
在公共区间内,增函数+增函数=增函数,增函数-减函数=增函数等.
y=f(x)与y=kf(x)(k≠0),当k>0时,增减性相同,当k<0时,增减性相反.
3.如何求函数在某闭区间上的最值
剖析:如果函数y=f(x)在闭区间[a,b]上具有单调性,那么它在这个区间上必取得最大值和最小值.即当f(x)在[a,b]上递增时,ymax=f(b),ymin=f(a);当f(x)在[a,b]上递减时,ymax=f(a),ymin=f(b).
如果函数y=f(x)在给定的闭区间[a,b]上不具有单调性,那么也就没有上述确定的结论了,那就要具体问题具体分析了.
讲练互动
【例题1】求函数y=|x+1|+|x-2|的单调区间,以及在每一个区间上的单调性.分析:本题考查单调区间的判定,在解题时应用数形结合思想,通过图象寻找单调区间.
图2-1-14
解:将函数化为分段函数形式:
y=
画出它的图象(图2-1-14),由图象,可知单调递增区间为[2,+∞),单调递减区间为(-∞,-1].
绿色通道
(1)函数的单调性是对某个区间而言的,若在某区间,函数值为唯一确定常数时,我们称函数在该区间没有单调性.(对于单独的一点,因为没有增减变化,所以显然不存在单调性问题)(2)对于闭区间上的连续函数来说,只要在开区间上单调,它在闭区间上也就单调,因此在考虑它的单调区间时,包括不包括端点都可以;还要注意定义域内不包含的点,不应出现在单调区间里.
(3)分段函数是历年高考的热门话题,常考常新,值得我们在平时认真对待.
变式训练1.已知函数f(x)=x2-5x+6.
(1)求其单调区间;
(2)用定义法证明其单调性.
分析:(1)运用函数图象找单调区间是求解函数单调性的基本方法.对于二次函数,其图象为抛物线.单调区间的界定与对称轴有关;而单调增减性与开口有关.所以考查二次函数问题,一定得两看(看二次项系数,看对称轴).
(2)定义作差法是证明函数单调性的一般方法,而有时通过定义作差法也可以直接找出单调区间.
解:(1)f(x)=(x)2,它是以(,)为顶点,对称轴平行于y轴、开口向上的抛物线,如图所示,可得单调区间是(-∞,]与(,+∞).
其中在(-∞,]上是减函数,在(,+∞)上是增函数.
(2)定义法证明如下:
任取x1、x2,设x1
=(x1+x2-5)(x1-x2).
∵x1
∴f(x)=x2-5x+6在(-∞,]上是减函数.
类似地,可以证明f(x)在(,+∞)上是增函数.
【例题2】讨论函数f(x)=x+(a>0)的单调性.
分析:可以先讨论函数在(0,+∞)上的单调性,然后可类似地讨论在(-∞,)、[,0)、(0,]上的单调性.
解:∵x≠0,∴下面先讨论f(x)=x+在(0,+∞)上的单调性.
设0
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
故f(x)在(0,]上是减函数.
∵当a≤x1
同理我们可得f(x)在(-∞,]上是增函数;f(x)在[,0)上是减函数.
黑色陷阱
判断单调性时,我们可以用口诀“同向则增,异向则减”帮助理解.在证明时,化简是必不可少的,不能想当然地认为谁大谁小而直接下结论,一般情况下,我们应该化简到出现因式相乘,或者出现完全平方式为止,然后通过已知条件对符号进行判断.含参数函数单调性的判定,往往对参数要分类讨论.本题的结论十分重要,在一些问题的求解中十分有用,应予重视.
变式训练
2.讨论函数y=(-1
解:设-1
∴当a<0时,f(x1)
当a=0时,f(x)为常数函数,没有单调性.
【例题3】判断函数f(x)=的单调性.
分析:可把函数的分子拼凑成分母的形式,转化成只在分母中含有变量x的形式,写出它的单调区间.解:原函数可化为f(x)=+1,该函数的定义域为{x|x≠1}.显然f(x)的图象是由y=的图象先向右平移1个单位,再向上平移1个单位而得到的.
由于y=在(-∞,0)上是减函数,在(0,+∞)上也是减函数,
从而f(x)=在(-∞,1)上是减函数,在(1,+∞)上也是减函数.
所以函数f(x)=在(-∞,1)和(1,+∞)上都是减函数.
绿色通道
把未知的问题转化为已知的问题,用已知问题的解还原说明未知问题的解,这是学好数学的一种常用方法.解决这种分式函数问题,需掌握“凑分母”化简的方法.变式训练
3.函数y=在(-2,+∞)上单调递增,则实数a的取值范围为.
解析:y===a.
因原式在(-2,+∞)上单调递增,
设-2
∴.
∵0
故实数a的取值范围是(1,+∞).
答案:(1,+∞)
【例题4】已知≤a≤1,若函数f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),令g(a)=M(a)-N(a).
(1)求g(a)的函数表达式;
(2)判断函数g(a)在区间[,1]上的单调性,并求出g(a)的最小值.
分析:(1)属于“轴变区间定”问题,需要对对称轴与区间的关系进行讨论.(2)由于g(a)是分段函数,其单调性的判断方法是分别将各个区间上的解析式单独判断,然后再结合各区间的单调性求最小值.
解:(1)∵≤a≤1,∴f(x)的图象为开口向上的抛物线,且对称轴为x=∈[1,3].
∴f(x)有最小值N(a)=f()=1.
当2≤≤3时,a∈[,],f(x)有最大值M(a)=f(1)=a-1;
当1≤<2时,a∈(,1],f(x)有最大值M(a)=f(3)=9a-5.
∴g(a)=
9a-6+,
∴g(a)在[,]上是减函数.
设
∴当a=时,g(a)有最小值.
绿色通道
求分段函数的单调性时,需对构成分段函数的各解析式分别进行判断.如果函数y=f(x)在区间[a,b]上单调递增,在区间[b,c]上单调递减,则函数y=f(x)在区间[a,c]上有最大值f(b);如果函数y=f(x)在区间[a,b]上单调递减,在区间[b,c]上单调递增,则函数y=f(x)在区间[a,c]上有最小值f(b).
变式训练
4.已知点P(t,y)在函数f(x)=(x≠-1)的图象上,且有t2-c2at+4c2=0(c≠0).
(1)求证:|ac|≥4;
(2)求证:在(-1,+∞)上f(x)单调递增;
(3)求证:f(|a|)+f(|c|)>1.
分析:在解决函数定义域、值域、比较两数大小、不等式的证明等具体问题中均可能用到函数的单调性,要充分运用,灵活处理.而一元二次方程的问题,有时往往可以根据需要去判定Δ的符号,从而得到不等式.本题还需运用分离常数法化简分式,要懂得借鉴.
解:(1)∵t∈R,t≠-1,∴Δ=(-c2a)2-16c2=c4a2-16c2=c2(c2a2-16)≥0.
∵c≠0,∴c2>0.∴c2a2≥16.∴|ac|≥4.
(2)由f(x)=,
设-1
∴f(x2)-f(x1)>0,即f(x2)>f(x1).
∴x>-1时,f(x)单调递增.
(3)∵f(x)在x>-1时单调递增,|c|≥>0,
∴f(|c|)≥f()=.
∴f(|a|)+f(|c|)≥f(|a|)+f()==1,
即f(|a|)+f(|c|)>1.
教材链接
[探索与研究]
函数值的改变量与自变量改变量的比叫做函数y=f(x)从x1到x2之间的平均变化率.
研究一个函数在某区间上是增函数还是减函数时,你能否根据函数的平均变化率,即比值的符号来判断函数y=f(x)在某区间上是增函数还是减函数 比值的大小与函数值增长的快慢有什么关系
答:当函数的平均变化率为正数时,可判断函数y=f(x)是增函数;当函数的平均变化率为负数时,可判断函数y=f(x)是减函数.比值的大小与函数值增长的快慢有关系:当越大时,函数值增长越快,当越小时,函数值减少就越快.
