初中数学苏科版八下 构造轴对称图形解题方法 教学案(含答案)
文档属性
| 名称 | 初中数学苏科版八下 构造轴对称图形解题方法 教学案(含答案) | 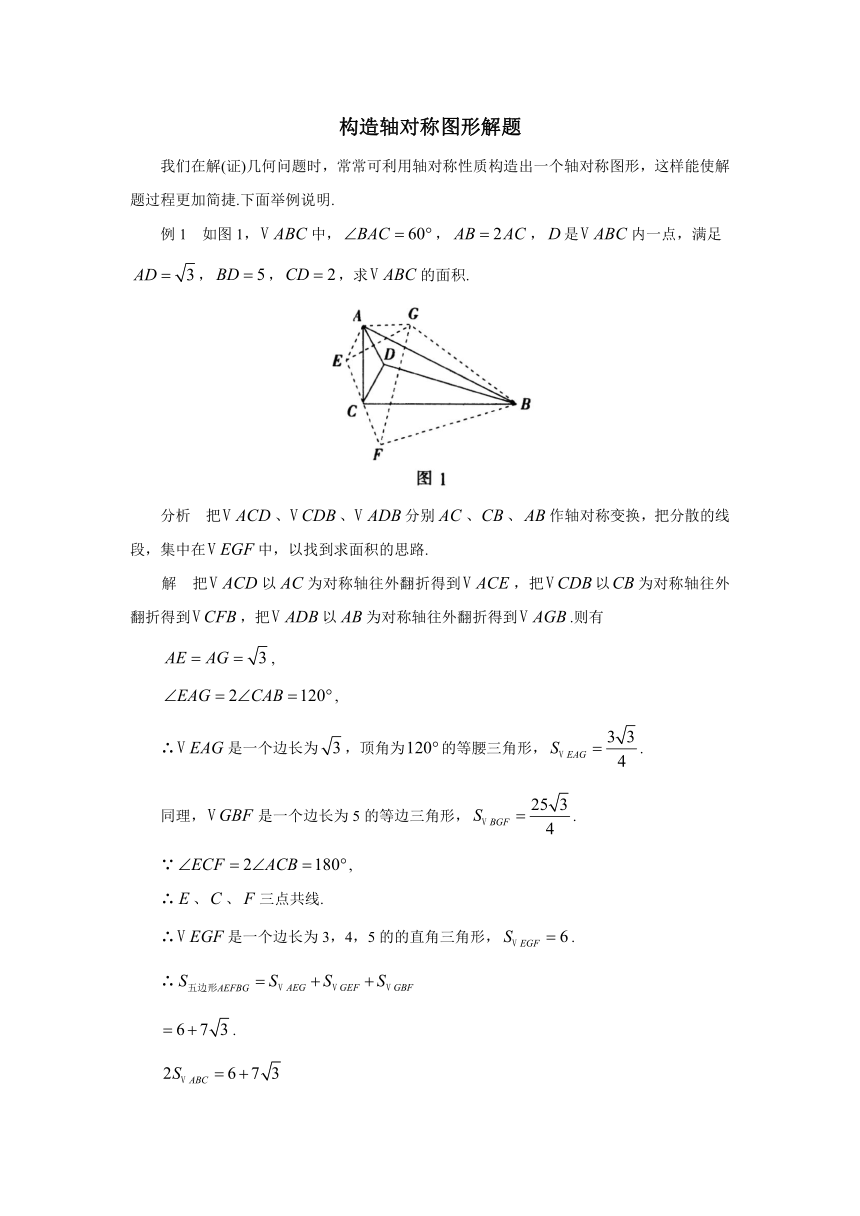 | |
| 格式 | zip | ||
| 文件大小 | 378.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2017-05-16 18:52:28 | ||
图片预览


文档简介
构造轴对称图形解题
我们在解(证)几何问题时,常常可利用轴对称性质构造出一个轴对称图形,这样能使解题过程更加简捷.下面举例说明.
例1
如图1,中,,,是内一点,满足,,,求的面积.
分析
把、、分别、、作轴对称变换,把分散的线段,集中在中,以找到求面积的思路.
解
把以为对称轴往外翻折得到,把以为对称轴往外翻折得到,把以为对称轴往外翻折得到.则有
,
,
∴是一个边长为,顶角为的等腰三角形,.
同理,是一个边长为5的等边三角形,.
∵,
∴、、三点共线.
∴是一个边长为3,4,5的的直角三角形,.
∴
.
∴.
说明
遇到正方形中分散的线段,构造轴对称图形,集中到同一个图形,利用勾股定理,方程等方面解决问题.
例2
在中,,是的中点,、在、上,,求证:.
分析
要证,联想到勾股定理,作以为对称轴的,将分散线段,,转移同一个直角三角形来解决.
证明
如图2,延长至点,使,连结,
∵与是关于以为轴的对称图形,∴.
,.
又∵,,
∴.
,.
.
由,得是直角三角形,
∴.
.
说明
遇到勾股数的线段,构造轴对称变换,再用三角形全等,把对应线段转化同一个三角形促使问题解决.
例3
如图3所示,中,,,,的平分线交于,求的长.
分析
由于平分,因此我们可以作为轴的对称变换.
证明
取中点,连结,交于点,易知和关于对称,.
由于,,∴.
延长至点,使,连结交延长线于.显然,和关于对称,且.
由于是的中位线,
,.
,,
,.
于是,.
说明
遇到特殊角的三角形,构造轴对称图形,利用特殊的直角三角形性质或三角形中位线性质,使线段成比例,分段求解线段的长.
例4
已知等边,在的延长线上,平分,点在射线上,点为上一点,连结,.若,是多少度.
分析
本题关键是构造关于的轴对称图形,则,于是转化为,且有,从而找到解题的途径.
解如图4,作点关于的对称点,交于点,从而可得
,
.
由,,在同一直线上,易证
,
从而,
,.
又由于,从而,
∴.
∴.
∴.
即,
∴.
说明
等腰(等边)三角形是轴对称图形,充分利用轴对称性质求解,是解决问题的关键.
例5
如图5,在正方形中,在上,,,在上,求与的长度和的最小值.
分析
利用是正方形的对称轴,连结,就是的对称线段,把所求与的长度和的最小值转化为求的最小
值.
解
因为为正方形,所以、是关于所在直线对称的对称点,连结,,由对称性知,,则的最小值为的最小值
而,由三角形三边关系,知
即最小值就是
在中,
.
所以的最小值是.
说明
遇到最短距离问题,一般都要利用轴对称的知识,在将问题转化两点线段最短来解决.
例6
如图6,四边形的对角线与,它们相交于点,,,,试说明线段的理由.
分析
题中,相对较分散,难以比较.注意到,,,于是可以分别以,为对称轴,作出对称点与,连结,,,这样就可以把有关线段相对集中到中.
解
分别以与为对称轴,作出对称点与,连结,,,则,,.
在中,,
在中,,
所以.
故.
说明
遇到线段不等的问题,通常考虑运用轴对称图形的知识,将分散的线段相对集中,在利用三角形的两边之和大于第三边来解决.
我们在解(证)几何问题时,常常可利用轴对称性质构造出一个轴对称图形,这样能使解题过程更加简捷.下面举例说明.
例1
如图1,中,,,是内一点,满足,,,求的面积.
分析
把、、分别、、作轴对称变换,把分散的线段,集中在中,以找到求面积的思路.
解
把以为对称轴往外翻折得到,把以为对称轴往外翻折得到,把以为对称轴往外翻折得到.则有
,
,
∴是一个边长为,顶角为的等腰三角形,.
同理,是一个边长为5的等边三角形,.
∵,
∴、、三点共线.
∴是一个边长为3,4,5的的直角三角形,.
∴
.
∴.
说明
遇到正方形中分散的线段,构造轴对称图形,集中到同一个图形,利用勾股定理,方程等方面解决问题.
例2
在中,,是的中点,、在、上,,求证:.
分析
要证,联想到勾股定理,作以为对称轴的,将分散线段,,转移同一个直角三角形来解决.
证明
如图2,延长至点,使,连结,
∵与是关于以为轴的对称图形,∴.
,.
又∵,,
∴.
,.
.
由,得是直角三角形,
∴.
.
说明
遇到勾股数的线段,构造轴对称变换,再用三角形全等,把对应线段转化同一个三角形促使问题解决.
例3
如图3所示,中,,,,的平分线交于,求的长.
分析
由于平分,因此我们可以作为轴的对称变换.
证明
取中点,连结,交于点,易知和关于对称,.
由于,,∴.
延长至点,使,连结交延长线于.显然,和关于对称,且.
由于是的中位线,
,.
,,
,.
于是,.
说明
遇到特殊角的三角形,构造轴对称图形,利用特殊的直角三角形性质或三角形中位线性质,使线段成比例,分段求解线段的长.
例4
已知等边,在的延长线上,平分,点在射线上,点为上一点,连结,.若,是多少度.
分析
本题关键是构造关于的轴对称图形,则,于是转化为,且有,从而找到解题的途径.
解如图4,作点关于的对称点,交于点,从而可得
,
.
由,,在同一直线上,易证
,
从而,
,.
又由于,从而,
∴.
∴.
∴.
即,
∴.
说明
等腰(等边)三角形是轴对称图形,充分利用轴对称性质求解,是解决问题的关键.
例5
如图5,在正方形中,在上,,,在上,求与的长度和的最小值.
分析
利用是正方形的对称轴,连结,就是的对称线段,把所求与的长度和的最小值转化为求的最小
值.
解
因为为正方形,所以、是关于所在直线对称的对称点,连结,,由对称性知,,则的最小值为的最小值
而,由三角形三边关系,知
即最小值就是
在中,
.
所以的最小值是.
说明
遇到最短距离问题,一般都要利用轴对称的知识,在将问题转化两点线段最短来解决.
例6
如图6,四边形的对角线与,它们相交于点,,,,试说明线段的理由.
分析
题中,相对较分散,难以比较.注意到,,,于是可以分别以,为对称轴,作出对称点与,连结,,,这样就可以把有关线段相对集中到中.
解
分别以与为对称轴,作出对称点与,连结,,,则,,.
在中,,
在中,,
所以.
故.
说明
遇到线段不等的问题,通常考虑运用轴对称图形的知识,将分散的线段相对集中,在利用三角形的两边之和大于第三边来解决.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
